一种高光谱图像压缩投影改进方案
2016-12-14贾应彪
贾应彪
(韶关学院信息科学与工程学院,广东韶关512005)
一种高光谱图像压缩投影改进方案
贾应彪
(韶关学院信息科学与工程学院,广东韶关512005)
在高光谱数据处理中,基于随机投影的降维算法研究开始受到关注,压缩投影主成分分析(CPPCA)是一种由随机投影值重构高光谱图像的有效方法.根据高光谱图像具备的空间相关性,基于CPPCA提出一种新的改进方案.先在空间维把高光谱数据转换至小波域并依据其高低频情况对数据进行分类,再在光谱维选择不同的抽样率参数进行随机投影;重构时,利用CPPCA重构方法分别恢复各类小波域数据,再在空间维进行小波反变换获得高光谱图像.仿真结果表明,与原有CPPCA方法相比,高光谱图像重构质量得到提高,尤其是在抽样率低于0.2的情况下,SNR指标提高超过10 dB.
高光谱图像;随机投影;压缩投影主成分分析;小波变换
高光谱成像技术是一种新型对地遥感技术,在对目标场景进行成像时,能够在紫外、可见光、近红外和中红外等较宽的电磁波谱区域内,为每个空间像元提供数十甚至数百个窄波段(通常波段宽度<10 nm)的光谱信息.高光谱图像中这些丰富的光谱成分为地物分类等相关分析提供了有用信息,但高维数据也给信息传输和存储带来挑战,并增加了数据处理的难度.高光谱遥感图像的降维操作已经成为一种很重要的预处理手段.传统的高光谱降维方法主要有主成份分析方法和独立成分分析方法.然而,这类方法的实现过程复杂,在资源受限的遥感平台(如星载平台)无法得到有效应用.
作为传统高光谱降维方法的一种替代方式,在发送端通过随机投影的方式实现降维操作,在接收端通过相关重构算法来恢复原始高光谱数据无疑有效避开了上述难题,将复杂的计算从编码端转移到了解码端[1].近年来广受关注的压缩感知理论[2-3]提供了一种从随机投影恢复原始稀疏信号的方法,在高光谱随机投影的数据恢复研究中,文献[4-5]针对按波段图像随机投影方式设计了相应的重构算法,文献[6]则针对整个高光谱数据随机投影的重构提出了相关方法.针对高光谱光谱维随机投影模式,文献[1]提出的压缩投影主成分分析(Compressive Projection Principal Component Analysis,CPPCA),获得了比普通压缩感知重构算法更优的重构性能以及更快的重构速度,受到业内广泛关注.
虽然CPPCA在高光谱随机降维后具备较佳的重构性能,但该方法还存在明显不足:在抽样率低时重构效果较差.针对此情况,文献[7]提出了一种基于分类的CPPCA重构方法,通过利用相对少量的训练值(地面真实值),把高光谱图像的投影域数据划分为若干子集(每个子集代表一个唯一的类),然后分别独立地使用CPPCA重构算法对每一组进行.该方法需要地面训练数据,但在许多实际应用场合并不一定能够获得这些信息.
针对CPPCA方法没有考虑高光谱图像具备空间相关性这一点,提出了一种改进方案.先对高光谱图像在空间维进行单层小波变换,再依据小波系数的高低频情况对数据分块并在光谱维压缩采样时采用不同的采样率.重构时,利用CPPCA方法对各块小波系数进行恢复,再进行小波反变换重构高光谱图像,获得了更高的图像重构精度.
1 CPPCA的基本原理
高光谱遥感图像通常由几十或几百个光谱波段图像数据构成,可以看作一个三维图像,每个像元对应一个光谱矢量,每个波段对应一个二维图像.一般情况下,高光谱图像可以表示成一个Nλ×Nx×Ny的3维数据立方体,其中Nλ为光谱波段的数目,Nx和Ny分别为2维空间的水平和垂直方向像素数目.为了更清晰地描述将要提到的高光谱随机投影模型,这里把高光谱数据立方体改用Nλ×Nxy的2维矩阵X来表示,其中Nλ为光谱波段的数目,Nxy为空间像素的数目且Nxy=Nx×Ny.很明显,矩阵X的行向量Xi对应各波段图像,列向量Nj为空间像素点对应的光谱维向量.
记Xmxm(m=1,…,Nxy),则矩阵X可改写成如下的数据形式:

式中向量.假设向量为零均值,则其协方差矩阵为:

PCA变换的目的就是寻找一个正交变换矩阵W来对Nλ维向量进行正交变换.对于给定的X中的向量Xm,其PCA变换为:

式中W可由下式来计算:

由此可知PCA变换的实现过程极其复杂.
假定有K个正交向量Pk构成K维子空间Ρ的基,P=[P1…PK]提供了一个到空间Ρ的正交投影,可以把P称为一个正交的Nλ×K矩阵,则由xm到Ρ的正交投影为:

考虑到基﹛Pk﹜,有,使得

协方差矩阵Σ的特征值满足:λ1(Σ)≥…≥λN(Σ),对应单位特征向量为Wn.同理,的特征分解为:,其中的列为单位特征向量,特征值为.这K个特征值λk称做李兹值,对应的K个特征向量为李兹向量[1]:

最后,规范化投影vn定义为wn到P的归一化正交投影:

CPPCA方法思想[1]:如果子空间P是随机选取的,X中的向量高度奇异分布,即特征值λk(Σ)与其他特征值充分分离,那么其相应的归一化投影vn将相当接近与里兹值对应的里兹向量uk.假设uk≈vk,CPPCA重构时使用一种基于凸集投影算法从来逼近前面L个特征向量wn.这些特征向量被组装成Nλ×L的矩阵Ψ,近似的PCA变换矩阵W的前L个列.CPPCA通过经过一个简单的线性最小二乘伪逆来求解恢复PCA变换系数:

再经过一个简单变换来估计原高光谱数据集:

2 基于单层小波变换的CPPCA方法
研究发现,原有的CPPCA模型假设信号位于某个未知但低秩的单个子空间,但并没有考虑高光谱图像信号的其他特征,如空间先验特征,即相邻点之间具备相似性,各波段图像具备空间光滑特性,这一特性的直接表现形式就是对各波段图像做二维小波变换后,其能量都集中在低频部分,即小波低频系数包含了图像的绝大部分信息.

图1 基于单层小波变换的CPPCA方案图
CPPCA改进方案思路见图1.对于二维空间图像,进行二维小波变换后图像低频子带包含的信息量远超高频子带,其对图像重构起到的作用更大.因此若对所有波段图像进行同样的单层小波变换,即将高光谱矩阵各行X1转换成Nx×Ny的二维形式,进行小波变换,变换后的高光谱小波域数据立方体为X^=,获得.小波分解将原图像分为高频子带和低频子带,按照空间分布情况,可将变换后的高光谱数据立方体按小波频带分成四个子立方体,然后对不同频带的子立方体采用不同采样率的光谱维随机降维处理,低频子立方体采用高采样率的压缩投影,高频子立方体采用低采样率的压缩投影,这样低频子立方体重构精度高,高频子立方体重构精度低,而低频子立方体对高光谱图像重构贡献大,整体重构精度得到提高.
具体实现方案如下:
步骤1:对高光谱数据X在各波段空间维上进行相同的单层小波分解,依据小波系数的高低频关系把分解后的数据分成和4个数据立方体.
步骤2:对4个高光谱数据立方体分别做光谱维随机降维,低频数据体进行高精度压缩采样,高频数据体进行低精度压缩采样.
步骤3:分别利用CPPCA方法恢复随机降维后的4个数据立方体,并将数据立方体合并在一起,在空间维做小波反变换恢复原高光谱图像.
3 实验结果与分析
采用了两组实验数据来测试方法的有效性,数据来自AVIRIS的Cuprite场景(http://aviris.jpl.nasa.gov),选取其中第1场景和第2场景的180波段高光谱图像(原数据集为224波段,去掉水汽分子吸收光谱等部分异常波段),各波段图像的大小选取为256×256.
表1对比了本文方法中调整不同数据体之间的抽样率分布对重构性能的影响,实验数据采用Cuprite第二场景的高光谱图像组,把得到的高光谱数据信噪比值(Signal to Noise Ratio,SNR)作为衡量重构性能的基本标准.由于低频数据体部分包含的信息量较大,对整个高光谱图像影响较大,因此可以适当提高低频数据体部分的采样率R1,在保证整个高光谱图像的抽样率R不变的情况下,高频数据体部分的抽样率Rh势必要降低.设△R为抽样率调整参数,实验中取值为△R=R-Rh,则R1=R+△R×3,随着△R的增加,高频数据体部分的抽样率降低,低频数据体部分的抽样率提高.由表1可知,在高光谱图像平均抽样率R较小时(如R<0.2),重构高光谱图像的平均信噪比随着△R的增加而增大,但当△R增加到一定程度后(△R=0.05),随着△R的进一步增加,平均重构精度反而有所下降.这是由于此时高频数据体部分的采样率很低,而CPPCA方法在采样率太低时,重构性能急剧下降.在高光谱图像平均抽样率R较大时(如R>0.2),改变△R对重构信噪比影响不大.在后面的仿真实验中,抽样率调整参数设置取△R=0.05.
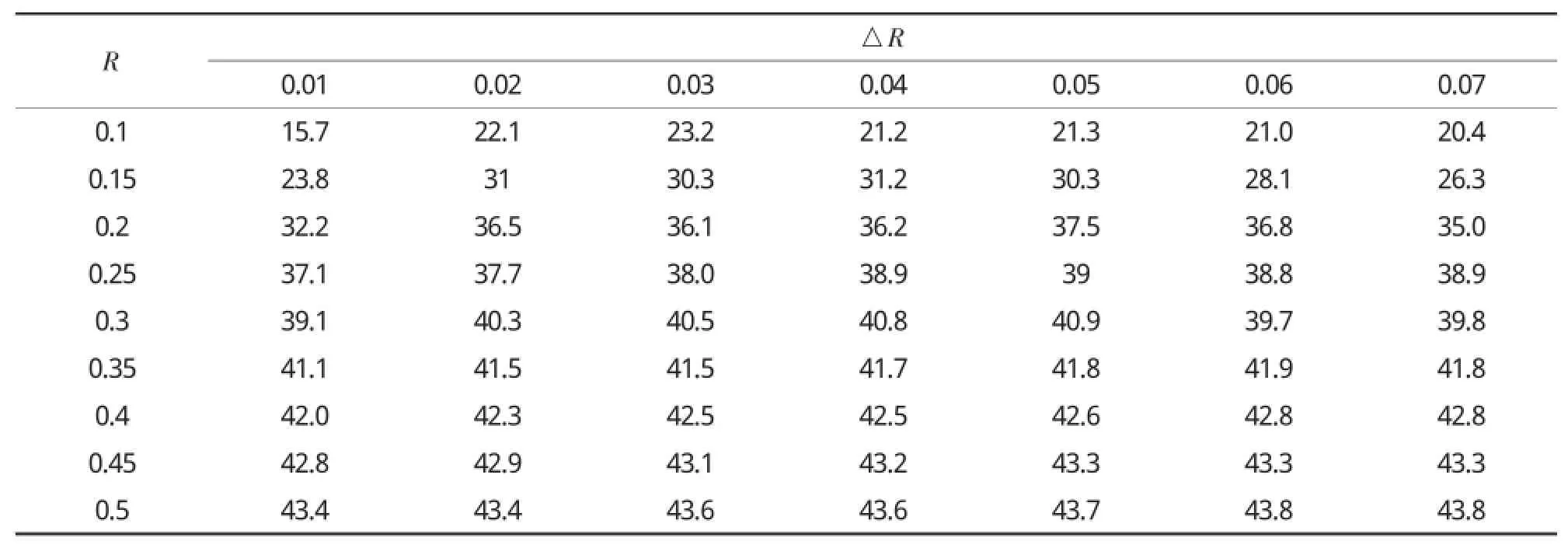
表1 不同抽样率调整参数下的信噪比(/dB)
图2比较了本文方法与单独采用CPPCA方法重构的信噪比.由图可知,对于两种不同场景,本文方法比单独采用CPPCA方法重构的精度提高比较明显,尤其在低抽样率情况下,本文方法提高超过10 dB.两个场景其中第一个场景纹理信息相对简单,第二个场景的纹理信息比较复杂,相应实验结论可推广至不同纹理复杂度的高光谱图像.
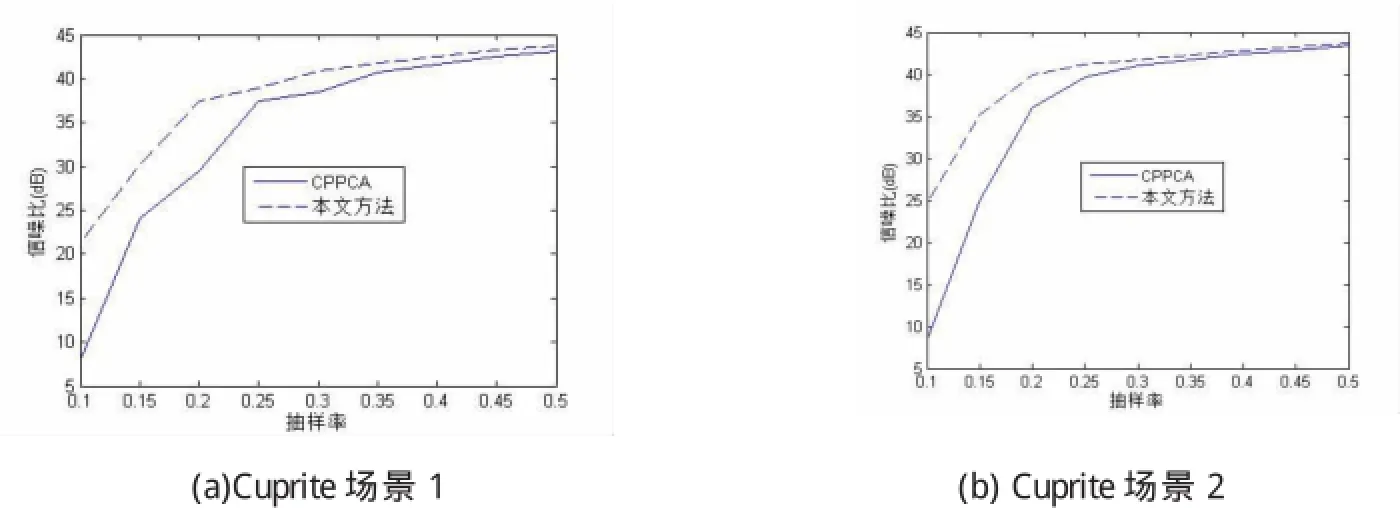
图2 本文方法与CPPCA重构方法性能对比
图3为两种方法的重构视觉效果图,由图可明显看出,CPPCA方法重建出的图像模糊不清,而本文方法重构出的图像已经较清晰,细节信息已经比较接近原图.

图3 不同方法重构效果图
4 结语
提出一种基于单层小波变换的高光谱图像分块随机投影和CPPCA重构方法,随机投影前先在空间维进行单层小波变换,再对不同高低频的数据立方体采用不同抽样率的随机投影;在重构数据时对各分块数据立方体采用CPPCA方法重构.实验结果表明本文方法比单独采用CPPCA方法重构精度能得到较大提高.此外,本文方法在降维过程中实现简单、不需要训练样本值,有利于在星载遥感平台这类资源受限场合得到实际应用.
[1]Flower J E.Compressive-projection principal com ponent analysis[J].IEEE Transactions on Image Process,2009,18(10):2230–2242.
[2]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[3]CandèS E,Romberg J,Tao T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incom plete Frequency Information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.
[4]计振兴,孔繁锵.基于谱间线性滤波的高光谱图像压缩感知[J].光子学报,2012,41(1):82-86.
[5]冯燕,贾应彪,曹宇明,等.高光谱图像压缩感知投影与复合正则重构[J].航空学报,2012,33(8):1466-1473.
[6]贾应彪,冯燕,王忠良.基于谱间结构相似先验的高光谱压缩感知重构[J].电子与信息学报,2014,36(6):1406-1412.
[7]Li W,Prasad S,Fow ler J E.Classification and Reconstruction from Random Projections for Hyperspectral Imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(2):833-843.
An Im proved Com pressive-projection M ethod of Hyperspectral Im ages
JIA Ying-biao
(School of Information Scienceand Engineering,Shaoguan University,Shaoguan 512005,Guangdong,China)
There is increasing interest in dimensionality reduction through random projections for Hyperspectral Images(HSI).Compressive-Projection Principal Component Analysis(CPPCA)is an efficient receiver-side reconstruction technique that recovers HSI data from encore-side random projections.According to the spatial correlation of HSI,an improved CPPCA method based on single layer wavelet transform is proposed in this paper. The wavelet coefficients of HSI is divided into several subsets and the random projection of different subset is implemented with varying dimensionality,such as a strong degree of dataset reduction for high-pass coefficients subset and a slight degree of dataset reduction for low-pass subset.For the reconstruction,CPPCA is used for each subset and then the HSI could be reconstructed by the inverse wavelet transform.Experimental results with HSI datasets reveal that the proposedmethod issuperior in performance compared to traditional CPPCA.
hyperspectral images;random projection;compressive-projection principal component analysis; wavelet transform
TP751.1
A
1007-5348(2016)08-0012-05
2016-06-13
广东省自然科学基金资助项目(2016A030307044);韶关市科技项目(441-99000311);韶关学院科研项目(314-140685).
贾应彪(1977-),男,湖南桃江人,韶关学院信息科学与工程学院讲师,博士;研究方向:高光谱数据分析、压缩感知及其应用.
(责任编辑:欧恺)
