相干MIMO雷达无模糊区面积缩小问题与优化扩展技术研究
2016-12-14张昭王小谟
张昭 王小谟
(1.北京理工大学信息与电子学院,北京 100081;2.中国电子科技集团公司电子科学研究院,北京 100041)
相干MIMO雷达无模糊区面积缩小问题与优化扩展技术研究
张昭1,2王小谟2
(1.北京理工大学信息与电子学院,北京 100081;2.中国电子科技集团公司电子科学研究院,北京 100041)
在时延-多普勒平面上,无模糊区面积决定雷达距离模糊与距离杂波折叠特性以及多普勒模糊与多普勒频率混杂特性.文章首次从理论上证明,采用N个波形的相干多输入多输出(Multiple-Input Multiple-Output, MIMO)雷达存在无模糊多普勒缩小现象,在一定条件下缩小为单输入-多输出(Single-Input Multi-Output, SIMO)雷达无模糊多普勒的1/N,导致该雷达无模糊区面积缩小为SIMO雷达的1/N,并给出了仿真实例.无模糊区面积缩小将导致雷达在杂波环境下性能下降.对此,提出了将相干MIMO无模糊区面积扩展到与SIMO雷达相等的波形设计技术,并给出恢复实例,解决了采用N个频率波形的相干MIMO雷达无模糊区面积缩小的基础性问题.
相干MIMO雷达;SIMO雷达;无模糊区面积;波形设计
DOI 10.13443/j.cjors.2015102301
引 言
距离杂波和多普勒杂波是机载雷达应用的基本约束.模糊函数是研究雷达匹配滤波器杂波处理性能的重要工具.多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达是当前研究热点[1-3].对于MIMO雷达,模糊函数清洁区特性已有报道[4-8],但无模糊区特性未见报道.
雷达模糊函数清洁区是指,在时延-多普勒平面上模糊函数中心峰周围无副瓣分布的区域[4,9].在清洁区内的杂波将被匹配滤波器滤除无输出,因此模糊函数清洁区面积反映了匹配滤波器滤除杂波的性能.对于采用N个正交波形的MIMO雷达模糊函数,清洁区面积减小为单输入-多输出(Single-Input Multi-Output, SIMO)雷达清洁区面积的1/N以下[5-8].清洁区面积减小被认为是MIMO雷达的重要限制,将限制雷达在机载条件下的应用[6];同时还被认为是MIMO雷达技术体制的致命缺陷[10].
与清洁区不同,在时延-多普勒平面上雷达信号模糊函数中心峰周围无栅瓣分布的区域称为无模糊区.无模糊区面积为无模糊时延与无模糊多普勒乘积的4倍[11].无模糊时延大小决定了雷达距离模糊和距离杂波折叠特性,无模糊多普勒大小决定了雷达多普勒模糊和多普勒杂波混杂特性.因此,雷达无模糊区特性对于雷达匹配滤波器的杂波性能有重要影响.本文主要研究相干MIMO雷达无模糊区特性及相关优化扩展技术.
1 相干MIMO雷达波形与模糊函数
1.1 探测波形
广泛应用的相干脉冲串雷达波形为[11]
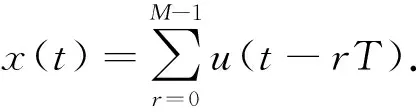
(1)
式中: M为脉冲串中的脉冲数目; T为脉冲重复周期; MT为相干脉冲串的相干处理时间;
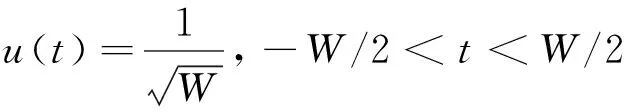
(2)
W为脉冲宽度.
假设相干MIMO雷达采用包括N个波形的频率波形组作为探测波形,表达式为
sn(t)= x(t)exp[j2π(n·ΔF)t],
n=1,2,…,N.
(3)
式中,ΔF是波形组中两个相邻波形间频率间隔,
ΔF·MT=A,
(4)
A为任意正整数.
1.2 模糊函数定义
相干MIMO雷达模糊函数定义为
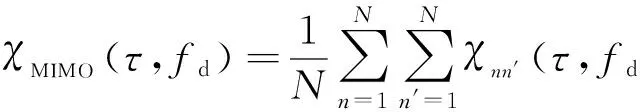
(5)
式中: 1/N为归一化因子; |χnn′(τ,fd)|是两个波形sn(t)和sn′(t)的互模糊函数,
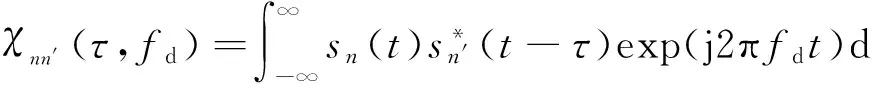
(6)
根据式(5),将关系式(3)和(4)代入(6)得到
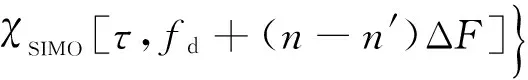
(7)
式中,χSIMO(τ,fd)为以单一波形x(t)为探测信号的SIMO雷达模糊函数:
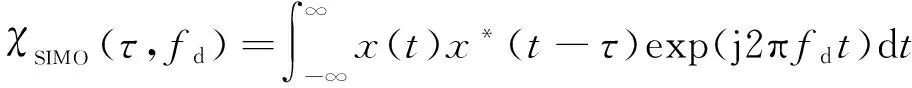
(8)
该模糊函数可写为[11]
χSIMO(τ,fd)=exp{j2πfd[τ+(M-1)T]}·
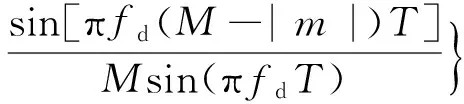
(9)
该SIMO雷达模糊函数栅瓣在时延轴和多普勒轴上的位置坐标为[11]
(10)
由式(10)可知:在SIMO雷达的时延轴上,时延栅瓣以T为间隔周期分布,无模糊时延为T;在多普勒轴上,多普勒轴栅瓣以1/T为间隔周期分布,无模糊多普勒为1/T.所以,SIMO雷达的无模糊区面积为4·T·(1/T)=4(无单位),这是对SIMO雷达的基本限制.
2 无模糊多普勒缩小现象
为分析相干MIMO雷达无模糊多普勒特性,在式(7)中令τ=0得到
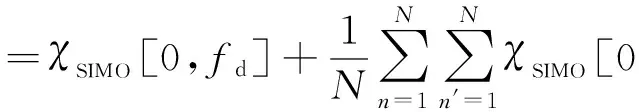
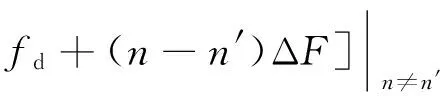
(11)
令n-n′=k,式(11)简化为
|k|/N)χSIMO[0,fd+kΔF].
(12)
式(12)表明,函数切片χMIMO(0,fd)由SIMO雷达函数切片χSIMO(0,fd)和一系列中心峰值平移到
fd=-k·ΔF(k=±1,±2,…,±(N-1))
(13)
位置的模糊函数切片χSIMO(0,fd+kΔF)叠加构成.
在式(11)中,SIMO雷达模糊函数切片为
χSIMO(0,fd)= exp[j2πfd(M-1)T]·
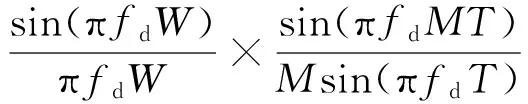
(14)
式中:等号右边第三项为类辛克函数,类辛克函数确定χSIMO(0,fd)的多普勒栅瓣周期间隔(即无模糊多普勒)为1/T; 第二项为辛克函数,是对第三项类辛克函数幅度的调制,但不改变多普勒栅瓣周期特性.因此,以x(t)为探测波形的SIMO雷达零时延切片χSIMO(0,fd)由一系列多普勒栅瓣构成,栅瓣周期为1/T[11].相应地,各平移切片χSIMO(0,fd+kΔF)也由一系列多普勒栅瓣构成,栅瓣周期也为1/T.但各栅瓣的位置相对于χSIMO(0,fd)向左平移了kΔF的距离.
根据式(11)和(12),各平移切片χSIMO(0,fd+kΔF)将对χSIMO(0,fd)栅瓣分布产生扰动,影响χMIMO(0,fd)的无模糊多普勒取值.下面分析最小平移量ΔF的取值对相干MIMO雷达χMIMO(0,fd)无模糊多普勒的影响.
当ΔF<1/T,即模糊函数χSIMO(0,fd+ΔF)的平移距离ΔF小于χSIMO(0,fd)的无模糊多普勒1/T时,χSIMO(0,fd+ΔF)的中心峰出现在式(11)中χSIMO(0,fd)的无模糊区域内fd=-ΔF处,从而使得χMIMO(0,fd)的无模糊多普勒减小为ΔF.特别地,当满足
ΔF=1/NT,
(15)
模糊函数的中心峰出现在χSIMO(0,fd)无模糊区的1/(NT)处,从而使得相干MIMO雷达的无模糊多普勒减小为SIMO雷达无模糊多普勒1/T的1/N.
当ΔF>1/T,即模糊函数χSIMO(0,fd+ΔF)的平移距离ΔF大于χSIMO(0,fd)的无模糊多普勒1/T时,将ΔF按照1/T进行分解:
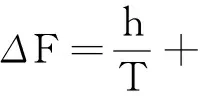
(16)
式中: h为将ΔF按照1/T进行展开的最大正整数; f为余数,f<1/T.式(16)表明,模糊函数χSIMO(0,fd+ΔF)相对于χSIMO(0,fd)向左平移的结果是,χSIMO(0,fd+ΔF)的中心峰值平移到fd=-ΔF处,同时χSIMO(0,fd+ΔF)的第h个栅瓣平移到χSIMO(0,fd)无模糊多普勒区间内fd=-f处,导致MIMO雷达模糊函数无模糊多普勒下降为F.进一步,如果F满足
f=1/NT,
(17)
则MIMO雷达模糊函数无模糊多普勒下降为SIMO雷达无模糊多普勒1/T的1/N.
综上所述,存在相干MIMO雷达无模糊多普勒相对于SIMO雷达缩小现象,并且存在特殊波形如式(15)、(16)和(17),使相干MIMO雷达无模糊多普勒下降到SIMO雷达的1/N.根据波形设计技术如式(4)、(16)和(17),设计表1所示的正交波形组参数,并对其模糊函数的零时延切片和零多普勒切片进行仿真,得到图1和图2.
图1表明相干MIMO雷达无模糊多普勒约为33 Hz.图2表明相干MIMO雷达无模糊时延为0.01 s.图3给出相干MIMO雷达模糊函数等高线图.如图3所示,表1中参数所确定的相干MIMO雷达无模糊区面积约为4×33×0.01≈4/3,下降到SIMO雷达无模糊区面积的1/3.此例表明:存在特殊波形组使相干MIMO雷达的无模糊多普勒下降到SIMO雷达的1/N;并且该波形组的无模糊时延与SIMO雷达的相等,导致相干MIMO雷达的无模糊区面积下降到SIMO雷达的1/N.

表1 波形组参数
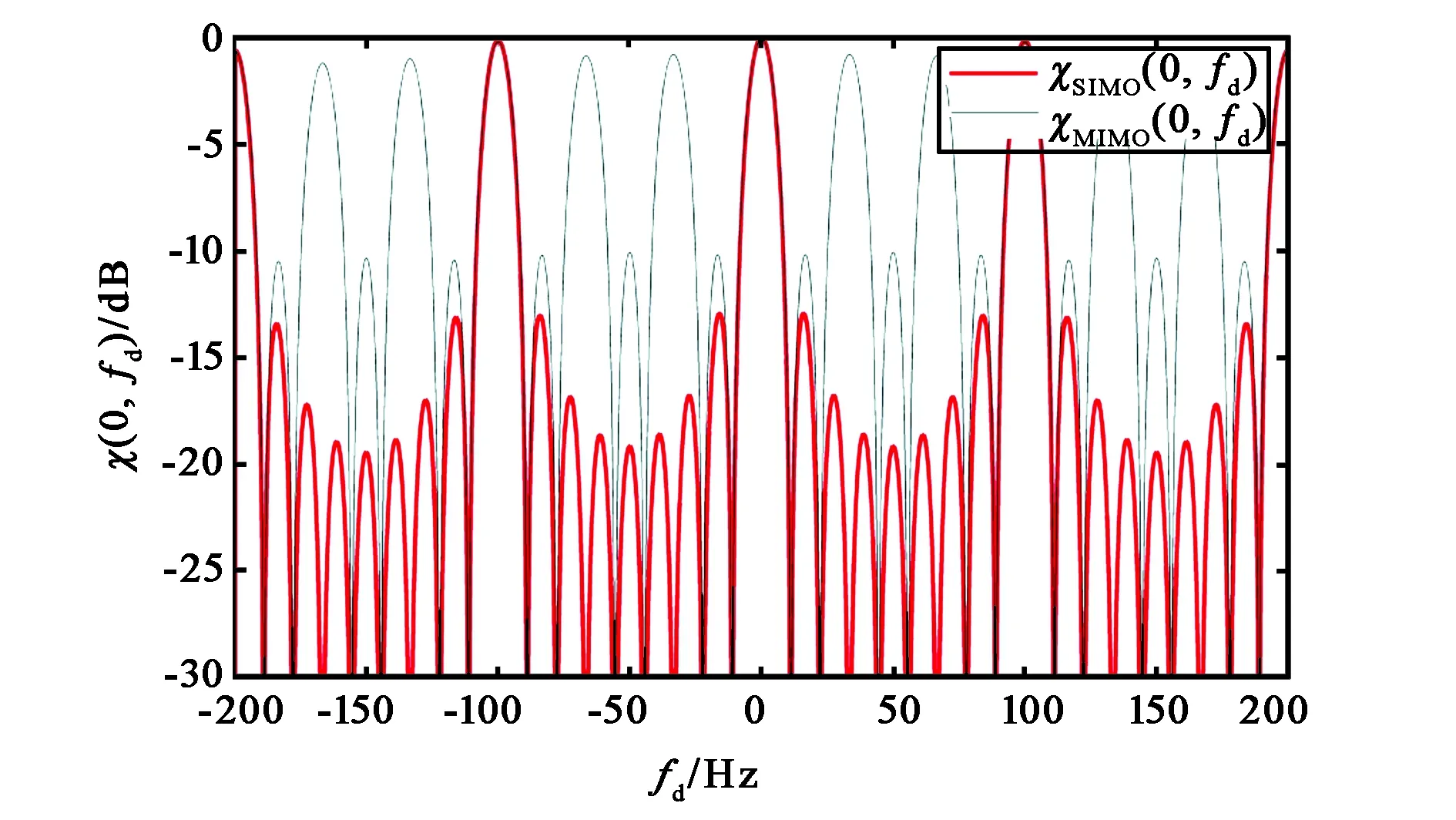
图1 相干MIMO雷达模糊函数零时延切片图
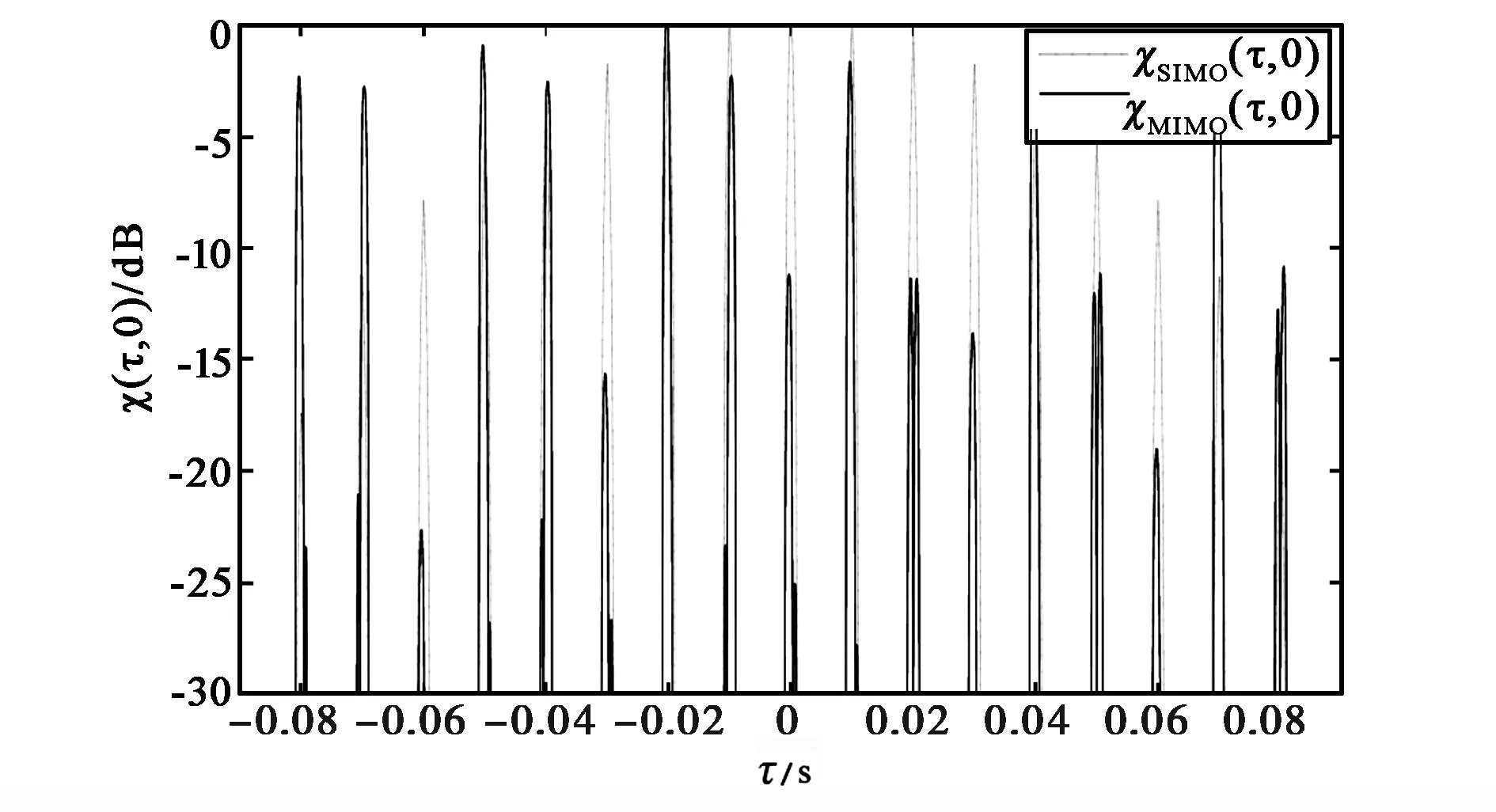
图2 相干MIMO雷达模糊函数零多普勒切片图
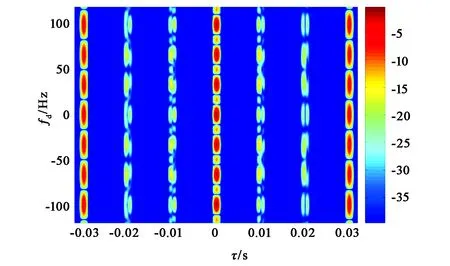
图3 相干MIMO雷达模糊函数等高线图(图右色尺单位为分贝)
雷达无模糊多普勒值和无模糊区面积的减小,将导致雷达杂波图中多普勒频率混杂问题恶化,在工程应用上将对雷达杂波性能产生不利影响,应引起重视.下节提出扩展相干MIMO雷达无模糊多普勒的频率波形组参数设计技术.
3 无模糊区面积优化扩展技术
3.1 无模糊多普勒优化设计
根据式(11)和(12),函数切片χMIMO(0,fd)由SIMO雷达函数切片χMIMO(0,fd)和平移的模糊函数切片χSIMO(0,fd+kΔF)叠加构成,其中χMIMO(0,fd)和χSIMO(0,fd+kΔF)的多普勒栅瓣周期间隔(即无模糊多普勒)都是1/T.因此,如果χSIMO(0,fd+kΔF)的周期栅瓣与χMIMO(0,fd)的周期栅瓣重叠,则叠加后的χMIMO(0,fd)栅瓣的周期间隔仍为1/T.基于这一思想,令ΔF取值为
ΔF=p/T,
(18)
P为正整数.则式(11)中各平移项χSIMO(0,fd+kΔF)的中心峰平移到χSIMO(0,fd)栅瓣kp/T处,使各平移项χSIMO(0,fd+kΔF)的栅瓣与χSIMO(0,fd)的栅瓣重合,因此,相干MIMO雷达模糊函数切片χMIMO(0,fd)的栅瓣间隔保持为1/T,即无模糊多普勒为1/T.
表2为根据波形设计技术式(4)和(18)设计的正交波形组参数,图4为其模糊函数零时延切片.图4显示,相干MIMO雷达的无模糊多普勒达到100 Hz,与相应SIMO雷达的无模糊多普勒1/T相等.在图4中,为避免相干MIMO雷达的零时延曲线与SIMO雷达发生重叠,相干MIMO雷达模糊函数切片的幅度未作归一化处理.

表2 波形组参数
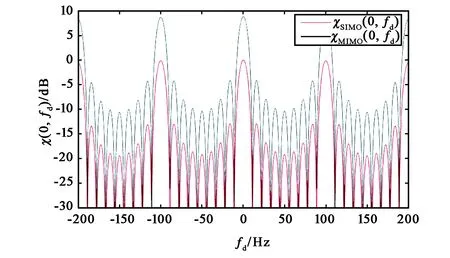
图4 优化后的相干MIMO雷达模糊函数零时延切片图
3.2 无模糊时延优化
上节提出使相干MIMO雷达无模糊多普勒扩展为1/T的波形优化设计技术式(18).本节证明,式(18)确定的波形优化设计技术能够使相干MIMO雷达无模糊时延保持为T,从而使相干MIMO雷达无模糊区面积与SIMO雷达相等.
为分析相干MIMO雷达的无模糊时延,在式(7)中令fd=0可得
χSIMO[τ,(n-n′)ΔF].
(19)
由式(9)可知,式(19)中,
χSIMO[τ,(n-n′)ΔF]
=exp{j2π(n-n′)ΔF[τ+(M-1)T]}.
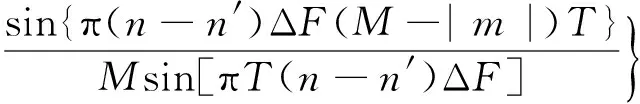
(20)
下面分析当ΔF取值满足式(18)时,在时延-多普勒平面上SIMO雷达栅瓣τ=mT处相干MIMO雷达是否存在栅瓣.将式(18)和τ=mT代入式 (20)可得
χSIMO[τ,(n-n′)ΔF]
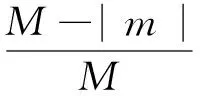
(21)
将式(18)、式(21)和τ=mT代入式(19)可得
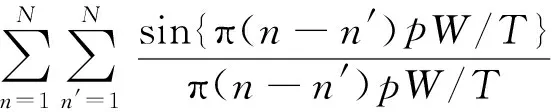
(22)
由式(9)和文献[11]可知,SIMO雷达模糊函数的零多普勒切片为
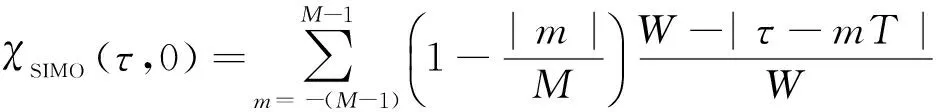
(23)
将τ=mT代入式(23)得到
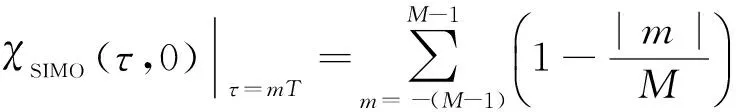
(24)
将式(24)代入式(22)可得
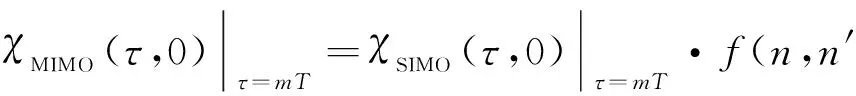
(25)
式中,
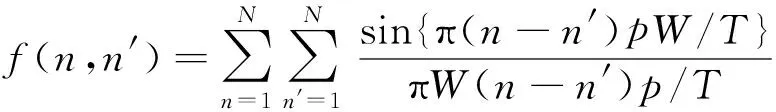
(26)
式(25)说明,MIMO雷达的时延栅瓣是SIMO雷达时延栅瓣与权函数f(n,n′)乘积的结果.式(26)表明,函数f(n,n′)的变量与式(24)中SIMO雷达时延栅瓣变量τ和m无关,因此,权函数f(n,n′)对所有时延栅瓣χSIMO(τ,0)|τ=mT进行相同的加权处理,不改变中心峰和各栅瓣的比例关系.由于模糊函数的幅度无绝对意义,经过归一化处理以后,该权函数可以忽略,即
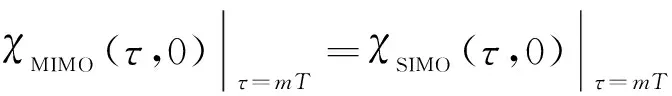
(27)
由式(27)可知,当满足式(18)时,MIMO雷达零多普勒切片中时延栅瓣的位置和幅度与SIMO雷达完全相同.因此,相干MIMO雷达的无模糊时延仍为T.根据式(27),由于相干MIMO雷达的无模糊多普勒为1/T,则无模糊区面积仍为4.采用表2中的波形组参数得到优化后的相干MIMO雷达模糊函数等高线,见图5.根据该图,无模糊时延为0.01 s,无模糊多普勒为100 Hz,则无模糊区面积为4.
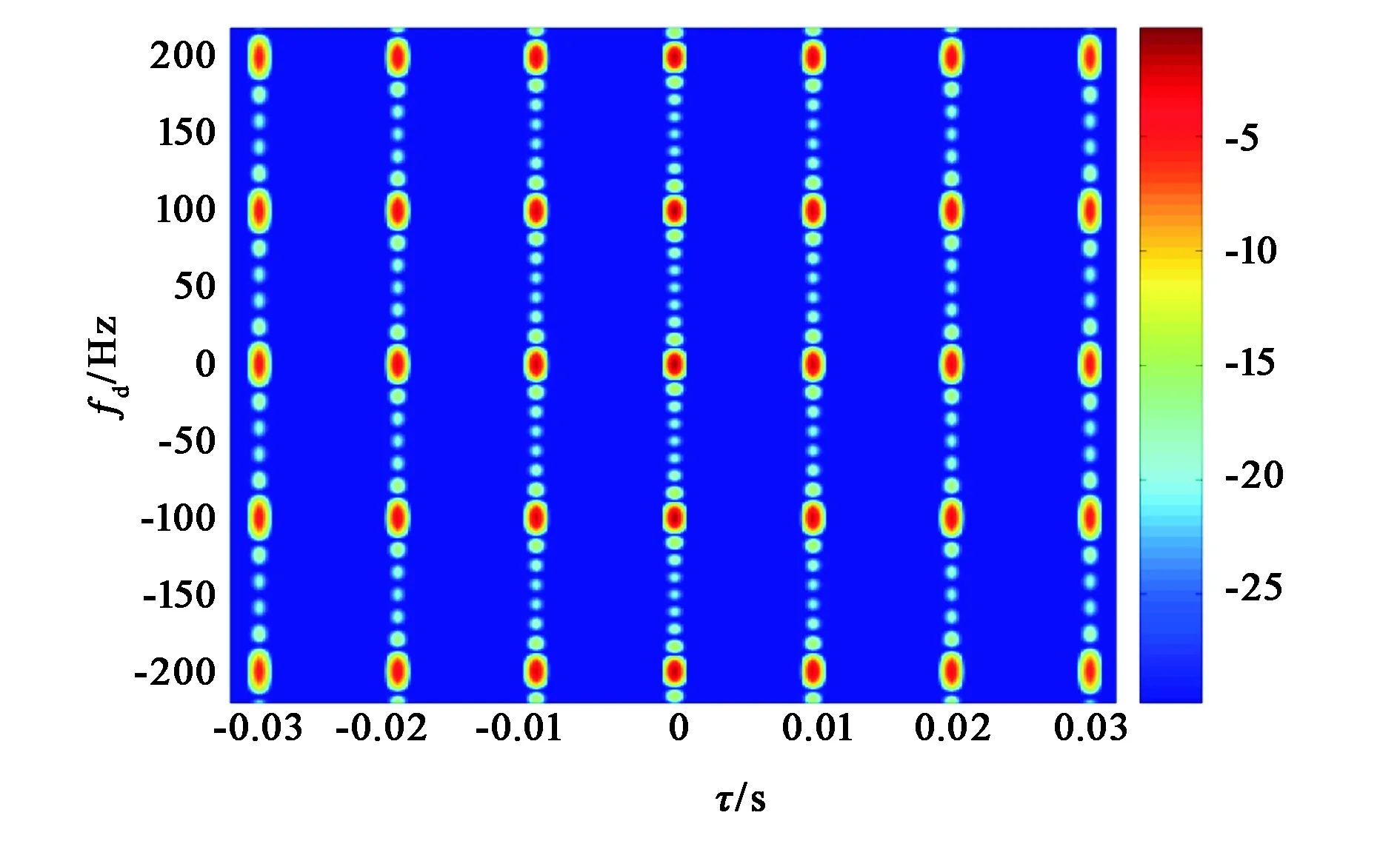
图5 优化后的相干MIMO雷达模糊函数等高线图(图右色尺单位为dB)
4 结 论
对于采用单一波形的SIMO雷达,距离模糊和距离杂波折叠特性由脉冲波形的重复周期决定,多普勒模糊和多普勒频率混杂由脉冲波形的重复频率决定.对于采用波形组的MIMO雷达,由于波形调制参数的增加,距离模糊、距离杂波折叠特性和多普勒模糊以及多普勒频率混杂特性不仅取决于脉冲波形的重复周期和重复频率,还取决于波形组参数.
本文首次从理论上证明,对于采用N个频率波形的相干MIMO雷达,根据波形组参数的取值情况,存在无模糊多普勒缩小现象,在一定波形条件下可能缩小到SIMO雷达无模糊多普勒的1/N.仿真结果给出相干MIMO雷达无模糊多普勒大小和无模糊区面积缩小为SIMO雷达的1/N的实例.
无模糊多普勒缩小将导致雷达多普勒模糊和多普勒频率混杂现象恶化,影响雷达测速和多普勒杂波处理性能.针对相干MIMO雷达无模糊多普勒缩小问题,本文进一步提出将相干MIMO无模糊多普勒扩展到与SIMO雷达无模糊多普勒相等的波形组优化设计技术,解决了采用频率波形组的相干MIMO雷达无模糊区面积缩小这一基础性问题.
[1] 吴梦, 刘宏伟, 周生华, 等. 阵列误差下的多输入多输出雷达测向技术[J].电波科学学报, 2014, 29(1): 158-164.
WU M, LIU H W, ZHOU S H, et al. Direction finding for MIMO radar with sensor mutual coupling and gain-phase errors[J]. Chinese journal of radio science, 2014, 29(1): 158-164. (in Chinese)
[2] 李军, 李会勇, 刘红明, 等. 基于多输入多输出技术的无源雷达信号模型[J]. 电波科学学报, 2011, 26(4): 802-806.
LI J, LI H Y, LIU H M, et al. Signal model of passive radar based on MIMO technique[J]. Chinese journal of radio science, 2011, 26(4): 802-806. (in Chinese)
[3] 陈刚, 顾红, 苏卫民. 分布式多入多出雷达相干处理二维分辨率分析[J]. 电波科学学报, 2014, 27(2): 326-332.
CHEN G, GU H, SU W M. Two-dimensional resolution of distributed MIMO radar with coherent processing[J]. Chinese journal of radio science, 2014, 27(2): 326-332. (in Chinese)
[4] SHARMA R. Analysis of MIMO radar ambiguity functions and implications on clear region[C]//IEEE Radar Conference, 2010, May 10-14, Washington D C. IEEE, 2010: 544-548.
[5] FRAZER G J, ABRAMOVICH Y I, JOHNSON B A. MIMO radar limitations in clutter[C]//IEEE Radar Conference, Pasadena, CA, May 4-8, 2009. IEEE, 2009:1-5.
[6] ABRAMOVICH Y I, FRAZER G J, JOHNSON B A. Noncausal adaptive spatial clutter mitigation in monostatic MIMO radar: fundamental limitations[J]. IEEE journal of selected topics in signal processing, 2010, 4(1): 40-54.
[7] ABRAMOVICH Y I, FRAZER G J. MIMO radar performance in clutter: limitations imposed by bounds on the volume and height distributions for the MIMO radar ambiguity function[C]//Proceeding of IEEE 5th Sensor Array and Multichannel Signal Processing Workshop SAM, Darmstadt, Germany, July 21-23, 2008: 441-445.
[8] ABRAMOVICH Y I, FRAZER G J. Bounds on the volume and height distributions for the MIMO radar ambiguity function[J]. IEEE signal processing letters, 2008, 15: 505-508.
[9] BHATT T D, RAJAN E G, RAO P V D S. Design of high-resolution radar waveforms for multi-radar and dense target environments[J]. IET radar sonar navigation, 2011, 5(7): 716.
[10]DAUM F, HUANG J. MIMO radar: snake oil or good idea? [J]. IEEE aerospace & electronic systems magazine, 2009, 24(5): 8-12.
[11]RICHARDS M A. Fundamentals of radar signal processing[M]. New York: McGraw-Hill, 2005: 183-187.
[12]WEINSTEIN S B, EBERT P M. Data transmission by frequency-division multiplexing using the discrete Fourier transform[J]. IEEE transactions on communication technology, 1971, 19(5): 628-634.

张昭 (1981-),男,山东人,在读博士研究生,主要研究方向为新体制雷达技术、多传感器智能化管理技术.

王小谟 (1938-),男,上海人,中国工程院院士,我国著名雷达工程专家.
Unambiguous area reduction problem and expansion techniques of coherent MIMO radar
ZHANG Zhao1,2WANG Xiaomo2
(1.SchoolofInformationandElectronicsBeijingInstituteofTechnology,Beijing100081,China; 2.ChineseAcademyofElectronicsandInformationTechnology,Beijing100041,China)
The unambiguous area in delay-Doppler plane is one of basic parameters of the radar, which determines the unambiguous range, the range-folding, the unambiguous Doppler and the Doppler-frequency aliasing properties. In this paper, for coherent (multiple-input multiple-output MIMO) radar using N frequency waveforms, the unambiguous Doppler is proved to be reduced, and in special conditions to be 1/N of the (Single-input multiple-output SIMO) radar unambiguous Doppler, accordingly, the unambiguous area of coherent MIMO radar is reduced to be 1/N of the SIMO radar unambiguous area. The simulation results display the unambiguous area reduction phenomenon. Furthermore, the paper advances waveforms designing techniques for expanding the unambiguous area of coherent MIMO radar to equal the area of the SIMO radar. The simulation results demonstrate the expansion of the unambiguous area.
coherent MIMO radar; SIMO radar; unambiguous area; waveform designing technique
10.13443/j.cjors.2015102301
2015-10-23
国家部委预研项目(7131020)
TN958
A
1005-0388(2016)04-0664-06
张昭, 王小谟. 相干MIMO雷达无模糊区面积缩小问题与优化扩展技术研究[J]. 电波科学学报,2016,31(4):664-669.
ZHANG Z, WANG X M. Unambiguous area reduction problem and expansion techniques of coherent MIMO radar [J]. Chinese journal of radio science,2016,31(4):664-669. (in Chinese). DOI: 10.13443/j.cjors.2015102301
联系人: 张昭 E-mail: zhangzhao_98@sina.com
