一种基于改进分布估计算法的统计模型选择

周本达，施明华，万甜甜，赵义超

(1.皖西学院 金融与数学学院，安徽 六安 237012；(2.皖西学院 金融风险智能控制与预警研究中心，安徽 六安 237012)



一种基于改进分布估计算法的统计模型选择

周本达，施明华，万甜甜，赵义超

(1.皖西学院 金融与数学学院，安徽 六安 237012；(2.皖西学院 金融风险智能控制与预警研究中心，安徽 六安 237012)

回归模型是数据处理中的经典分析方法，在许多领域都有重要应用。回归模型的模型选择的常用方法是专家选择和完全模型法，但两者都过于依赖主观经验，影响系统的运行效果。针对选择回归模型问题的特点,在分布估计算法基础上设计了相应的概率矩阵, 以赤池信息准则(AIC)和贝叶斯信息准则(BIC)作为模型选择的度量标准，提出了解决统计模型选择问题的改进分布估计算法。该算法基于遗传算法变异思想构造变异算子,基于免疫机理设计选择策略。最后，通过实例，将新算法与传统的遗传算法，以及经典的模型选择方法进行仿真比较，得出新算法在AIC、BIC值等各种指标上效果提高。

统计模型；模型选择；免疫选择策略；分布估计算法

多元统计分析中的回归分析方法是一种广泛的数据处理法，它主要根据已知数据建立拟合程度良好的回归模型。建模过程涉及2个核心问题，即如何从众多解释变量当中选取重要变量(变量选择)以及如何选择恰当的函数表达形式(变换选择)，一般称为模型选择问题。其实质相当于以下优化问题：利用调查数据对变量进行取舍、函数形式确定，建立变量间的相互依赖形式，使某种度量标准(统计准则)最优[1]。基本方法有逐步回归(stepwise regression)、专家选择、完全模型法(Complete Modeling)等，但它们过于依赖建模者的主观经验和建模过程。近年来，随着分布估计算法、遗传算法和粒子群算法等智能算法技术的发展，一些学者将智能算法用于求解此类问题，并取得不错的效果[1，2]。

分布估计算法 (Estimation of Distribution Algorithm, EDA)采用一种新型的进化机制，以遗传算法(GA)的遗传机制为基础，将统计学习规则和GA的隐并行性进行了有机结合，从而可以充分利用种群的全局信息建立个体的概率分布模型，依据概率模型对整个解空间进行学习、抽样产生新解，实现种群进化[3-6]。EDA在没有破坏积木块结构的基础上，既继承了GA通用、并行和强鲁棒性特点，又克服了传统算法对初始化敏感的缺点，可以大幅提高求解质量和效率[5]。但基本的EDA不能直接利用进化过程中的局部信息，也没有考虑种群中个体的多样性，更没有设计比较好的机制对局部最优解进行控制[7]。另外，基本分布估计算法没有考虑种群中个体的多样性，尤其在迭代后期会影响算法寻优性能，免疫算法[8]模拟免疫系统，依据抗体浓度构建繁殖策略，可以有效地保持种群多样性[8]。但免疫算法中抗体浓度的计算方法很多(如基于信息熵、欧氏距离、二进制的海明距离等)，各有优劣，目前采用较多的是信息熵方法，但信息熵方法对二进制编码抗体间的相似度和浓度无法度量，对于间断函数或变化幅度较大的函数定义相似度和浓度度量也不太精确[8]，并且其运行速度也较缓慢。

本文将以基本的分布估计算法为基础，拓展个体编码方式，设计反映统计模型中变量选择和变换选择的选择矩阵，定义选择矩阵对应的概率模型矩阵。同时，结合免疫机理定义种群中个体相似度和个体浓度，计算个体期望生存概率，据此设计免疫选择策略和自适应变异算子，改进概率模型的更新方法，提出一种求解模型选择问题的改进分布估计算法。

1 分布估计算法及其改进

分布估计算法解决问题的一般过程是：首先建立解空间的个体分布概率模型，然后对当前种群进行适应度值计算评估，依据选取规则选择优势个体组成候选集，采取统计学习手段更新对应的概率模型，再依据抽样规则对概率模型进行抽样，产生下一代种群[5]。

1.1 模型选择问题

1.2 选择矩阵及其对应的概率矩阵

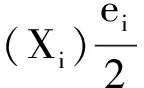
设计选择矩阵分别为：F=(fij)m×4和G=(gij)m×12，其中，若ti取集合T中第j元素fij=1，否则fij=0；且若ei取集合E中第j元素gij=1，否则gij=0。对应的概率矩阵分别为P=(pij)m×4和Q=(qij)m×12，其中，pij∈[0,1]且∑jpij=1；qij∈[0,1]且∑jqij=1。分别表示ti取集合T中第j元素的概率和ei取集合E中第j元素的概率。

1.3 适应度函数(Fitness function)

赤池信息准则(Akaike Information Criterion，AIC)主要基于信息论角度设计，其目标是使模型拟合信息损失达到最小，其中信息损失是由真实模型与候选模型间的Kullback-Leibler距离来度量[11-12]；而贝叶斯信息准则(Bayesian Information Criterion，BIC)主要是基于贝叶斯统计角度考虑，与AIC 信息相比，BIC的右边第2项中用logn代替了数值2，即考虑模型参数个数时，BIC比AIC的惩罚力度更大[13]。

1.4 概率模型及其更新

设第t代某个体的概率矩阵为P=(pij(t))m×4和Q=(qij(t))m×12，其对应的分类矩阵为：F=(fij(t))m×4和G=(gij(t))m×12，选取N个个体进行更新，则第t+1代的概率pij(t+1)为：

(1)

1.5 免疫选择

依据免疫算法的免疫选择策略设计如下：设个体长度为l，种群规模为N。

定义2 个体间相似性：设种群中两个体A1和A2的适应度值分别为g1和g2，设常数r>0和m>0，若有H(A1，A2)≤r且|g1-g2|≤m，则称个体A1与A2是相似的。

定义3 个体浓度：种群中与个体Ai相似的个体个数ni(包含Ai)称为个体Ai在种群中的浓度[5]。

由定义4可见，个体期望生存概率与适应度成正比，与浓度成反比，这样既能保证算法的收敛速度，又能保持个体的多样性[5]。

1.6 变异算子

分布估计算法利用可行解在解空间概率分布，产生概率模型来描述搜索空间中，再从模型中抽样产生新解，可以说分布估计算法有效地利用了解空间的全局统计信息。但每代发现局部最优解的局部信息并不能直接被EDA使用。因此，本文利用免疫算子度量个体间的相似性，据此设计自适应变异算子来克服EDA的这一缺陷[5]。

设A为变异个体，设i∈[1,m]和s∈[m+1,2m]，变异算子把个体A=(a1,a2,…,a2m)变异为B=(a1,a2,…ai-1,b,…as-1,c,…,a2m)，其中，b∈T且b≠ai，c∈E,且c≠as。自适应的变异概率pm如下：

(2)

注：在进化初期，种群中的不同个体数较多，变异概率较小；在进化后期，种群中的不相似个体数较少，变异概率较大。自适应变异有效拓展了算法的开采能力。

2 分布估计算法的改进

求解模型选择问题的改进分布估计算法步骤如下：

Step2 适应度值计算，并判断是否满足终止条件。若满足，算法结束，否则继续；

Step6 依据概率矩阵从更新后的优势群体中采样N次，得到新一代种群，转Step2。

3 实验与分析

文章采用Bilkent University DataSets[5，9]、UCI DataSets[5，10]提供的标准算例在MATLAB 2010a环境下测试，并同stepwise regression、Complete Modeling、标准遗传算法(SGA)和佳点集遗传算法(GGA)[14,15]进行比较。

算法参数设置为：种群规模为200，最大迭代代数为300，学习速率α为0.4，每个算例执行100次。在试验中我们将样本数据集分成两部分，75%的数据进行拟合，余下数据用于检验，并记录算例运行100次的AIC和BIC最优值(BestVideo)、平均值(Ave)、平均收敛代数(AveGen)以及找到最佳值的平均用时(单位：秒)，记录结果表1和2所示。

表1和表2中的SGA、GGA和IEDA等智能算法在求解回归模型时，准则值指标要好于完全模型法和逐步回归法，处理大规模数据时表现尤为突出，例如，对于Fat算例，三种智能算法无论在何种准则下都比完全模型法和逐步回归法缩小50%以上。免疫选择策略中个体期望生存概率的利用充分保证了改进的分布估计算法的整体寻优能力，同时，集合遗传算法的变异操作，及大地提高了算法开采能力。因为采用自适应变异概率，尤其在迭代后期能保证所有的采样区域都能被采样点覆盖，因此，IEDA的平均寻优时间和收敛代数比SGA和GGA好，所搜索到的最优解是最好的。

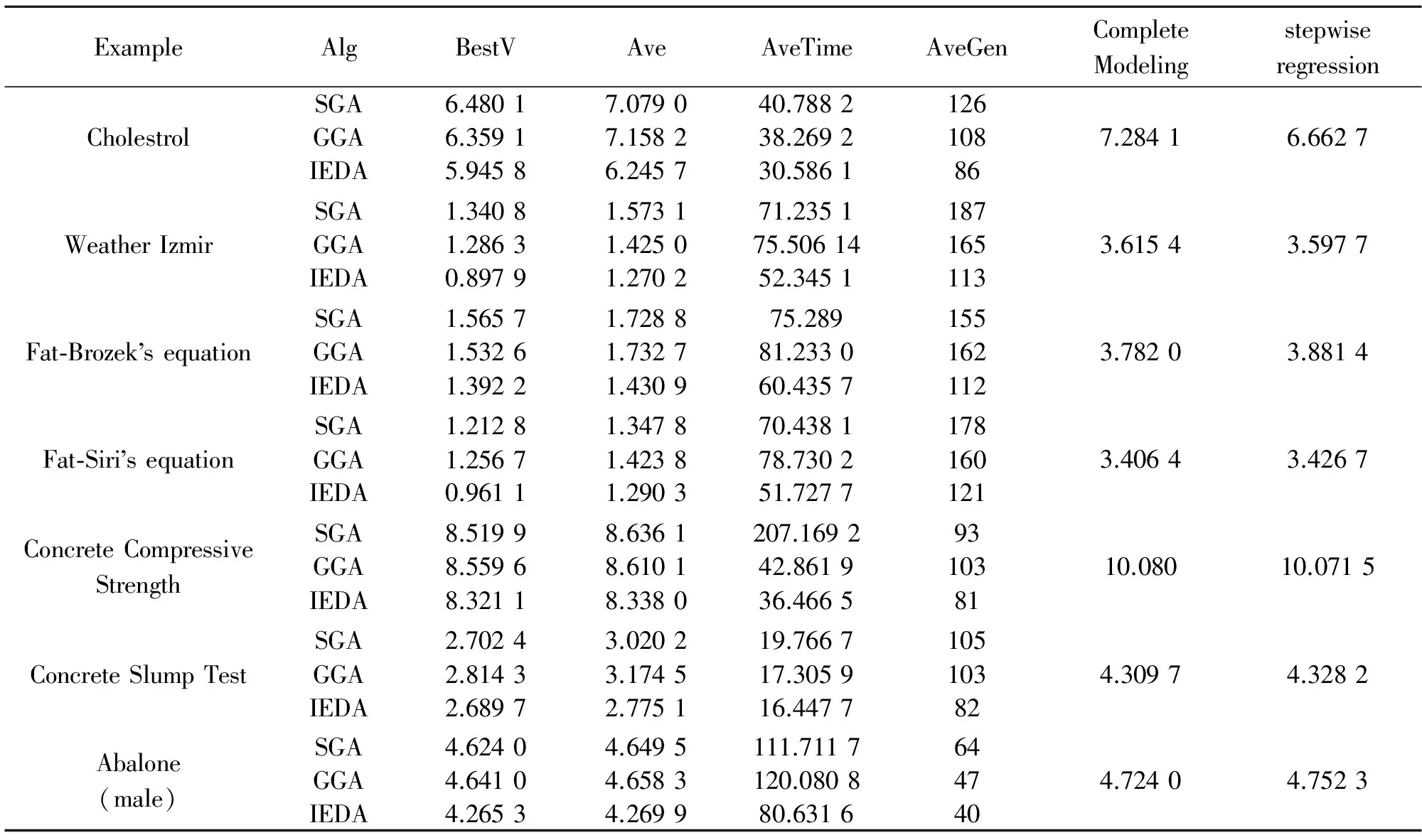
表1 AIC值的计算结果

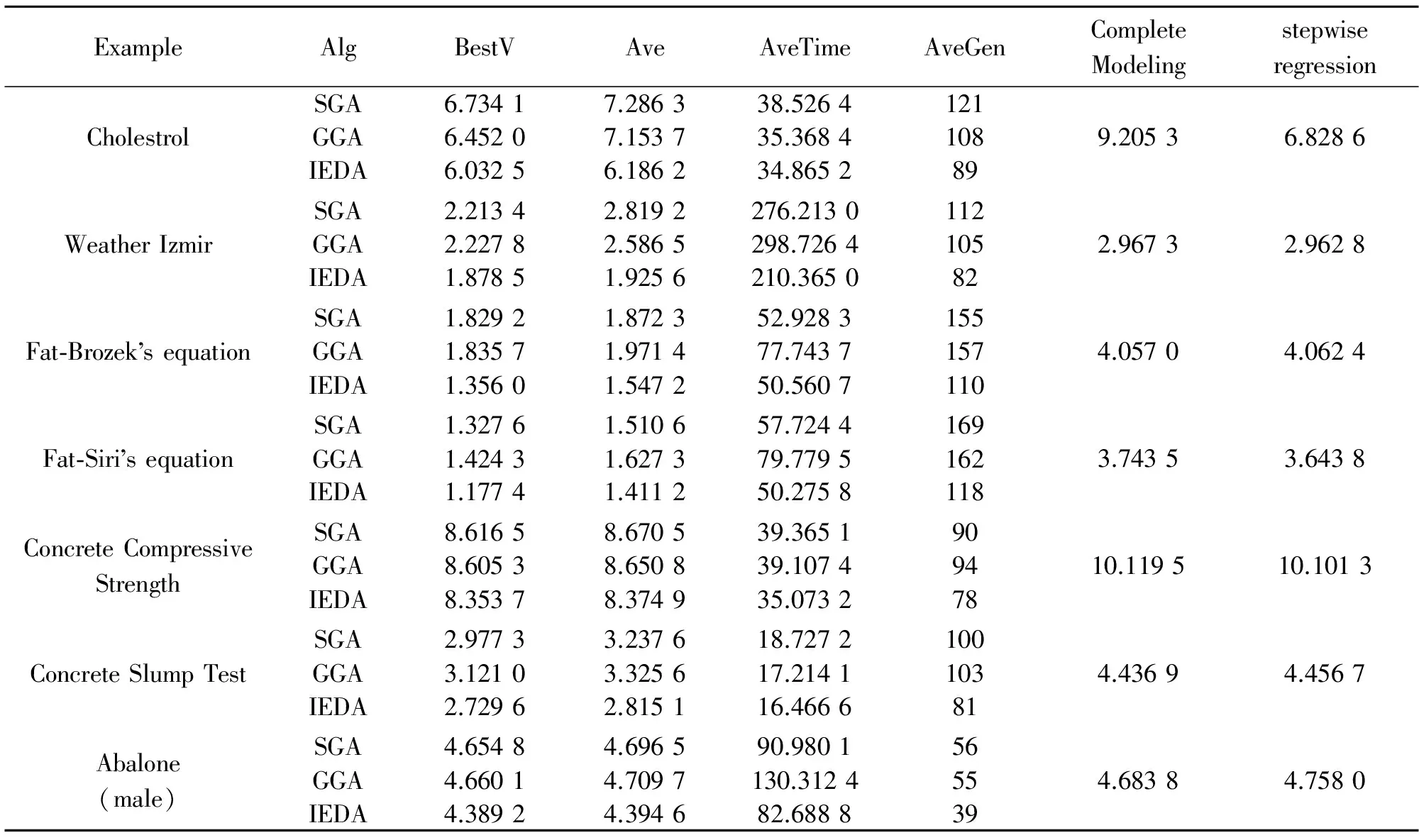
表2 BIC值的计算结果

4 结论(Conclusions)

文章基于回归模型选择问题的AIC和BIC度量方法，结合遗传算法中的变异算子对基本分布估计算法进行了改进，设计能对变量选择和函数变换并行实施的智能求解算法，克服了逐步回归、完全模型等传统方法求解回归模型选择问题时依靠主观经验和较强路径依赖性等缺点。回归模型选择问题求解的实验结果表明：基于算法融合思想对分布估计算法的改进提高了计算效率、有较稳定的计算结果，充分显示了其良好的寻优性能，比传统回归方法有较大程度的改进。

[1]SANDRA PATERLINI, TOMMASO MINERVA. Regression Model Selection Using Genetic Algorithms [C]. RECENT ADVANCES in NEURAL NETWORKS, FUZZY SYSTEMS & EVOLUTIONARY COMPUTING, 2010: 19-27.

[2]施明华，周本达，陈明华.基于均匀设计抽样的改进遗传算法在回归模型中的应用[J].计算机应用，2012，32(11)：3050-3053.[3]Aimin Zhou, JianyongSun, Qingfu Zhang. An Estimation of Distribution Algorithm With Cheap and Expensive Local Search Methods[J].IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION,2015,19(6):807-822.

[4]Hauschild M, Pelikan M, Lima C, et.al. Analyzing Probabilistic Models in Hierarchical BOA on Traps and Spin Glasses[C]//Proc. of GECCO’07. London, UK: IEEE Press, 2007.[5]周本达，姚宏亮，李国成.一种求解聚类问题的分布估计算法[J].计算机工程，2011，37(22)：191-195.

[6]周树德，孙增炘.分布估计算法综述[J].自动化学报，2007，33(2)：113-124.

[7]Li Shuzhuo, Chen Yinghui, Du Haifeng,et.al. A Genetic Algorithm with Local Search Strategy for Improved Detection of Community Structure[J]. Complexity, 2010,15(4):53-60.[8]周本达，姚宏亮，陈明华.一种改进拉丁方抽样免疫遗传算法[J].计算机应用研究，2011，28(4)：1283-1285，1289.

[9]Bilkent University,Function Approximation Repository[EB/OL].http://funapp.cs.bilkent.edu.tr/DataSets/, 2016-04-18.

[10]UCI Machine Learning Repository[EB/OL].http://archive.ics.uci.edu/ml/index.html/,2016-04-18.

[11]吕纯濂，陈舜华，杨勇杰.线性模型中变量和变换的同时选择[J].数值计算与计算机应用，2005，4(1)：26-35.

[12]KELVIN G. BALCOMBE, Model Selection Using Information Criteria and Genetic Algorithms[J]. Computational Economics, 2005, 25:207-228.

[13]贾桂文，张景川.基于BIC准则模型选择的光纤光栅波长温度拟合研究[J].传感技术学报，2014，27(2)：217-219.

[14]张铃，张钹.遗传算法机理的研究[J].软件学报，2000，11(7)：945-952.

[15]张铃，张钹.佳点集遗传算法[J].计算机学报，2001，24(9)：917-922.

A Statistic Model Selection Based on the Improved Estimation of Distribution Algorithm

ZHOU Benda, SHI Minghua, WAN Tiantian, ZHAO Yichao

(1.SchoolofFinance&Mathematics,WestAnhuiUniversity,Lu’an237012,China; 2.FinancialRiskIntelligentControlandPreventionInstitute,WestAnhuiUniversity,Lu’an237012,China)

Regression model is a classical analysis method in data processing. It has numerous applications in many fields. The most commonly-used methods are expert selection and complete model method. However, they are too dependent on the subjective experience. According to the characteristics of regression model selection problem, we design the corresponding probability matrix. Then, by combining Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC), we present an improved estimation of distribution algorithm for solving statistical model selection problem. It constructs mutation operator based on the idea of mutation of GA. Moreover, the selection policy is designed on the basis of the immune mechanism. Finally, we use computer simulation to compare this improved EDA, traditional genetic algorithm and classical algorithm for model selection and to show that the new EDA has superiority in AIC, BIC and other various indices.

statistical model; model selection; selection strategy of immune; estimation of distribution algorithm

2016-07-04

安徽省高校省级自然科学研究重点项目(KJ2016A742)；皖西学院校级自然项目(WXZR201619)；六安市定向委托皖西学院市级研究项目(2009LW018)。

周本达(1974-)，男，安徽六安人，教授，硕士，研究方向：智能算法、金融网络、计算金融。

O212.4

A

1009-9735(2016)05-0033-05