我国银行业系统性风险结构度量——基于尾部依赖视角

蒋 涛1，李政宵2

(1.对外经济贸易大学 金融学院，北京 100029；2.中国人民大学 统计学院，北京 100872)



我国银行业系统性风险结构度量
——基于尾部依赖视角

蒋 涛1，李政宵2

(1.对外经济贸易大学 金融学院，北京 100029；2.中国人民大学 统计学院，北京 100872)

根据系统性风险的定义，系统性风险可以拆分为金融机构之间的风险传染以及风险传染之间的相依关系。Copula函数可以作为度量系统性风险的一种新方法，并具备很多优良性质。在此基础上引入C藤copula，该方法不仅可以度量出系统性风险的大小，而且可以度量出系统性风险中的传染结构，使得风险度量结果更加合理。运用C藤copula对我国银行业系统性风险结构进行了实证分析，结果表明，可以从控制商业银行之间风险传染的微观审慎监管以及控制银行之间风险传染之间的相依性的宏观审慎监管两个层面来对银行业系统性风险进行管理。

系统性风险；风险传染；传染结构；C藤copula

0 引 言

自2008年金融危机以来，系统性风险受到业界和学界的广泛关注。根据FSB(Financial Stability Board)[1]对系统性风险的定义，系统性风险主要包括两个层面内容：一个是金融系统中部分机构受到损失而给整个金融服务带来损失，另一个是对实体经济产生负面影响。该定义主要强调了金融机构之间的风险传染而引起了系统性的危害。BIS(Bank for International Settlements)[2]和IMF对系统性风险的定义与之类似，是指某家金融机构违约(或者经营失败)通过影响其他金融机构，最终影响金融稳定。除此以外，系统性风险还包括了大部分金融机构因面临宏观经济因素的冲击而共同面临的风险。例如，大萧条时期，美国9 000多家商业银行的倒闭也是系统性风险。[3]因此，系统性风险不仅包括金融机构之间的风险传染，而且包括金融机构共同面临的宏观经济冲击的风险。从系统性风险的特征上看，可以利用金融机构的风险相依性来刻画风险传染和宏观经济冲击两个方面系统性风险。

系统性风险管理的核心在于对系统性风险的度量。目前，系统性风险度量方法层出不穷，但是还没有一个公认的标准度量方法。就现有系统性风险度量来看，主要包括宏观层面的度量方法和微观层面的度量方法。其中，宏观层面的系统性风险度量主要从系统性风险带来的危害出发，通过对金融系统或宏观经济的指标体系来描述。例如，CATFIN[4]、信号法修正模型[5]等。但是，宏观层面系统性度量方法忽视了不同金融机构在系统性风险(或系统性危机)中的差异化表现(不同规模、不同经营风格的金融机构对系统性风险的贡献是不相同的)以及金融机构之间的交互作用(或者风险传染)。这使得基于宏观层面的系统性风险的管理存在一些漏洞。

微观层面系统性风险度量恰好可以弥补宏观层面度量方法的缺陷。一些学者通过利用微观金融机构数据来分析金融机构之间的交互效应、风险传染来描述系统性风险，这些度量方法包括条件在险价值(CoVaR)和边际期望损失(MES)。自Adrian & Brunnermeier[6]提出利用CoVaR和MES来度量金融机构对其他金融机构或者金融系统的风险溢出度量。此后，该方法被广泛应用于系统性风险度量上。但利用CoVaR和MES来度量系统性风险和该方法提出的初衷是不相符的。CoVaR和MES度量单个金融机构的风险溢出，也即是单个金融机构在系统性风险中的贡献，无法体现出系统性。

针对CoVaR和MES方法中无法体现出系统性这一缺点，谢远涛、等[7]提出利用尾部依赖的思想来对系统性风险的度量。该方法主要是考虑金融系统中的大部分或者全部金融机构，利用copula函数对这些金融机构风险的尾部依赖大小来度量系统性风险。蒋涛、等[8]进一步对该方法进行了拓展，利用时变copula对金融业系统性风险进行了动态度量。

截止目前，基于copula对系统性风险的度量充分考虑到了系统性，度量出了一个系统性风险的指标，却忽视了个体金融机构之间的风险传染、风险相依的结构。系统性风险强调金融机构之间风险传染。一些研究发现系统性风险具有顺周期性，也就是在经济上行时期，系统性风险较小；而在经济下行时期，银行业系统性风险会显著增加。从微观金融主体商业银行的特征来看，商业银行之间的风险传染在周期中会表现出同质性。因此，银行业系统性风险可以分为两个层面来考虑：银行之间风险传染以及这些风险传染之间的系统性。

第一，金融机构之间风险传染。金融机构之间风险传染的影响因素包括金融机构的规模和金融机构之间的关联度等。首先，金融机构的规模是一个重要的影响因素。一些研究显示了金融业存在“大而不倒(too big to fall)”现象[9]。也即是一些金融机构由于自身规模因素在整个金融业中具有重要地位，这类金融机构一旦倒闭或者面临破产风险会对其他金融机构乃至整个金融业产生强烈冲击作用，影响金融系统稳定。其次，金融机构间的关联度。一些学者指出金融机构面临的系统性风险实际上也就是“太关联而不能倒”(too interconnected to fall)的问题[10]。金融机构由于在日常经营活动中难免会与其他金融机构有一定的业务往来、资产互持等关联，而正是由于这种关联性增加了金融机构之间的风险相依性。

第二，金融机构间风险传染之间的相依性。不仅两家金融机构之间传染强度增加，实际上这种金融机构间传染相依性随着市场状况的变化而发生变化。例如，公允价值计量和流动性等因素对金融机构之间的风险传染有着相同的作用机制，呈现出了风险传染之间的同质性。Brunnermeier & Pedersen[11]从市场流动性和融资流动性视角出发通过理论分析发现，危机时刻金融机构之间风险暴露的相关性系数均增加。蒋涛、等[8]基于尾部依赖对银行业、证券业和保险业系统性风险动态度量，从三个行业尾部依赖来看，尾部依赖的走势呈现出了较高的相关性。吴卫星、等[12]通过我国银行业研究了融资流动性与系统性风险之间存在螺旋式增长结构，而该结果实际上也就是融资环境对金融机构之间风险相依性有着共同的影响。由此，可以看出金融机构之间风险传染也表现出了相依性。

综上，系统性风险度量可以从金融机构间传染本身以及风险传染之间的相依性来度量。为了从该视角进一步完善系统性风险微观度量，本文引入C 藤 copula函数对系统性风险进行度量。基于C 藤 copula系统性风险度量不仅可以对系统性风险强度进行度量，而且可以对风险传染或者风险相依的结构进行度量。

1 基于copula系统性风险度量模型

传统copula在度量系统性风险时，是将单个金融机构的风险累积分布函数(cdf)作为边缘分布，利用copula函数来度量这些金融机构之间的风险相依来刻画系统性风险。在本文中，为了刻画系统性风险中金融机构之间的风险传染结构，同时体现系统性，可引入C Vine copula对金融机构风险相依结构和强度进行系统度量，以此来对系统性风险进行度量。

1.1 基于copula系统性风险度量

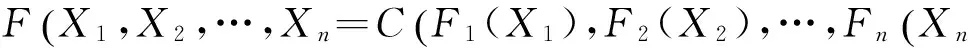
(1)

联合密度函数可以表示为不同边缘分布的密度函数f( )和一个copula函数c( )，如(2)所示：

(2)

这其中可以利用copula函数c( )来度量银行风险之间的传染性，特别是危机时刻(风险分布的尾部)风险传染性。

1.2 基于C 藤 copula系统性风险度量

根据不同银行之间风险传染的异质性，拟通过银行之间风险传染以及风险传染之间的相依性来刻画系统性风险的结构。这里引入C 藤 copula，C 藤 copula实际上是一个配对的思想，将银行系统的联合密度函数表示成多个由两元copula函数形式，这里也即允许银行之间的风险传染存在异质性。根据Czado et al.[13]，C 藤 copula可以表示为

(3)

(4)

利用C 藤 copula度量系统性风险时，首先利用不同的金融机构的风险分布作为边缘分布，通常利用广义自回归条件异方差模型(GARCH)或者随机波动模型(SV)。然后利用C 藤 copula来刻画金融机构之间的风险传染强度和风险传染结构。例如，当度量一个包括三家商业银行机构(这里利用1，2，3来表示)的银行系统时，我们可以得到如图1所示的风险传染结构。

图1 含三家银行的银行业系统性风险结构示意

图1表示银行业的系统性风险结构。首先，根据与其他金融机构的风险传染强度的大小来选择与其他金融机构风险传染强度总和最大的银行(商业银行1)。进一步可以分别得到银行1与其他家商业银行之间的风险相依强度，如图1中上半部分所示。其中，1和2之间的连线表示商业银行1和银行2之间的风险传染性，通过利用尾部依赖系数可以得到风险传染强度。1和3之间的连线的解释类似。但是，比较1和2以及1和3之间的风险传染，允许两者之间存在传染性的差异。

由于商业银行风险传染之间可能存在相依性，进一步对该相依性进行刻画。在以商业银行1为条件的基础上，可以进一步得到银行1和2之间传染与银行1和3之间风险传染之间的相依性(如图1下半部分所示)，以及相依的强度。

这里仅仅描述了包含三个银行的银行系统中系统性风险度量状况。当银行系统性中包含多个银行时，仍然可以通过利用多元(由银行个数决定)C 藤 copula来度量系统性风险。随着商业银行个数的增加，银行业系统性风险的结构将更为复杂。

2 基于copula系统性风险度量性质

利用copula对系统性风险度量的优势在蒋涛等[8]的文章也有提到，但是并没有细化和明确。本文将对基于copula系统性风险度量性质进行具体说明。引入C 藤 copula函数对系统性风险度量可以满足以下几点性质。

2.1 系统性

系统性风险与其他类型风险的主要区别在于系统性。系统性风险强调风险主体不是单个金融机构，而是整个金融系统。那么，在系统性风险度量中如果仅仅考虑单个金融机构的风险，或者单个金融机构对其他金融机构的风险溢出会显得有些单薄。基于copula函数系统性风险度量的系统性体现在，该方法度量时可以将所有的金融机构或者一些重要的金融机构纳入度量范围，利用每一家金融机构的风险作为边缘风险，引入copula函数，以此来对系统性风险度量。可以看出，基于copula系统性风险度量不再局限考虑单个金融机构风险，而是考虑了多家或者全部金融机构的风险因素。因此，该方法可以满足系统性风险度量的系统性。

2.2 传染性

系统性风险的另一个主要特征是金融机构之间的风险传染，其来源于金融机构之间的业务往来、负面信息溢出、市场挤兑或者宏观经济影响等。因此，在系统性风险度量时需要考虑金融机构之间的风险传染特征。基于copula系统性风险度量主要是度量金融机构风险相依性。因此，系统性风险的传染性质同样在copula度量方法得到了体现。

2.3 内生性

Adrian 和 Brunnermeier[6]指出系统性风险度量需要满足内生性要求。那么，从copula度量方法的计算上来看，基于copula系统性风险度量同样可以满足内生性要求。

2.4 时变性

不同时期系统性风险是会发生变化的，这对系统性风险度量提出了时变性的要求。由于copula函数已拓展至时变copula[14]。利用时变copula既可以完成对系统性风险的动态度量，体现系统性风险度量的时变性。可参见蒋涛、等[8]一文中利用时变copula对金融业系统性风险进行了实证分析。

2.5 传染结构

基于C 藤 copula对系统性风险度量对系统性风险度量性质进行了一个拓展，即是对风险传染结构的度量。现有基于copula函数系统性风险度量往往是采用多元copula对系统性风险整体度量，但是该度量结果虽然很好地指示了系统性风险走势，但却不利于具体分析系统性风险传染结果。在系统性风险度量性质拓展至传染结构层面将更加有利于系统性风险的防范和管理。

3 数据及描述性统计

3.1 数据来源

本文将利用C 藤 copula对我国商业银行业系统性风险进行实证分析。在数据选取上，仍然沿用谢远涛、等[7]和蒋涛、等[8]利用金融机构股票市场数据来分析。主要是考虑到股票市场日度数据可以较为有效反映金融机构市场风险，本文利用2008年1月1日至2014年3月31日我国七家系统性重要银行股票数据进行分析。数据来源于WIND咨询数据库。

3.2 描述性统计

由于仅考虑7家系统性重要银行，所以C 藤 copula中的n取值为7。首先，我们对7家商业银行对数收益率的统计量进行简单的描述性分析(见表1)。从表1可以看出，7家商业银行的对数收益率分布呈现出了尖峰和厚尾。因此，本文分别将利用ARMA(1,1)-GARCH(1,1)作为7家商业银行风险的边缘分布，以此来进一步分析商业银行的系统性风险。

表1 我国七家商业银行股票对数收益率描述性统计量

4 实证分析

4.1 我国商业银行风险依赖分析

前文已述基于copula对系统性风险度量方法是将所有商业银行风险分布作为边缘分布度量风险传染，这实际上忽视了商业银行的异质性。为了验证商业银行对系统性风险贡献的差异，将对不同商业银行之间的风险依赖大小进行分析。

图2显示了我国7家商业银行两两配对的依赖密度。从图2中，可以清晰看到7家商业银行之间均存在明显的尾部依赖现象。分别比较这种商业银行风险的尾部依赖，同样可以看出不同的商业银行之间的风险依赖(特别是风险的尾部依赖)存在差异。由于商业银行之间风险传染存在差异，那么在系统性风险度量中不能将这些商业银行视为同质的，需要对不同商业银行之间的风险传染进行测度。这为度量出系统性风险结构的必要性提供了佐证。

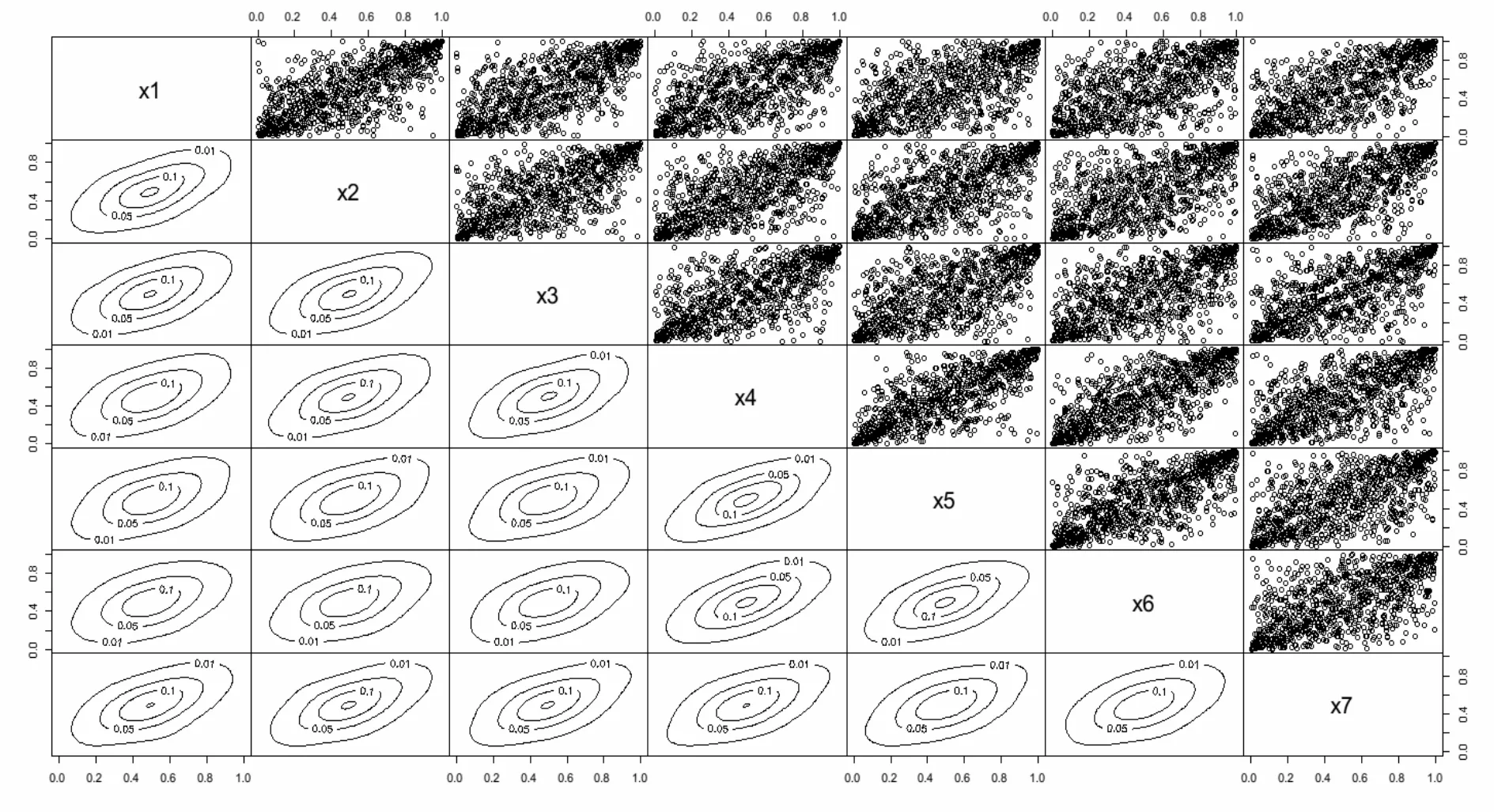
图2 七家商业银行配对依赖密度图

4.2 我国商业银行业系统性风险度量

进一步，利用C 藤 copula对我国商业银行业系统性风险进行度量。如表2所示，可以得到商业银行两两之间的依赖强度。比较每家商业银行与其他家商业银行之间的风险依赖强度大小，可以发现商业银行x4与其他商业银行的风险传染强度总和最大。该结果显示了，一些商业银行在整个商业银行风险传染中的重要地位。当金融机构发生危机时刻，危机最有可能会传导至商业银行x4，并通过x4这家商业银行传导至其他商业银行。

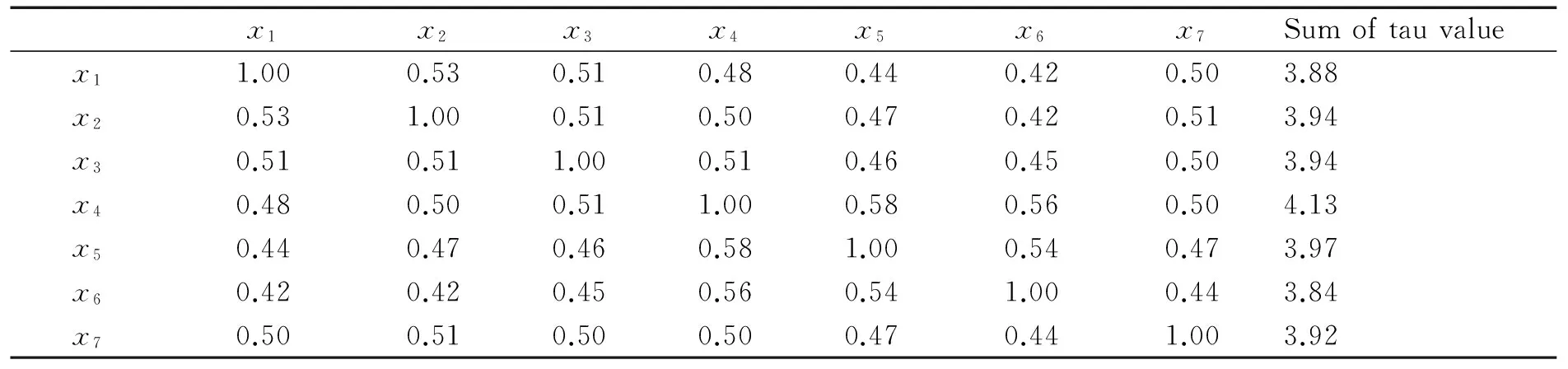
表2 商业银行之间风险相依大小度量

在以商业银行x4风险为条件的基础上，可以进一步计算剩下的其他家商业银行之间的风险传导强度。其结果类似与表2，通过比较可以找出第二家风险传染强度最大的商业银行。以此类推，最终得到了类似于树状的结构，这里为了清晰了解商业银行之间传染的结构，笔者将商业银行之间的风险传染结构整理在图3中。

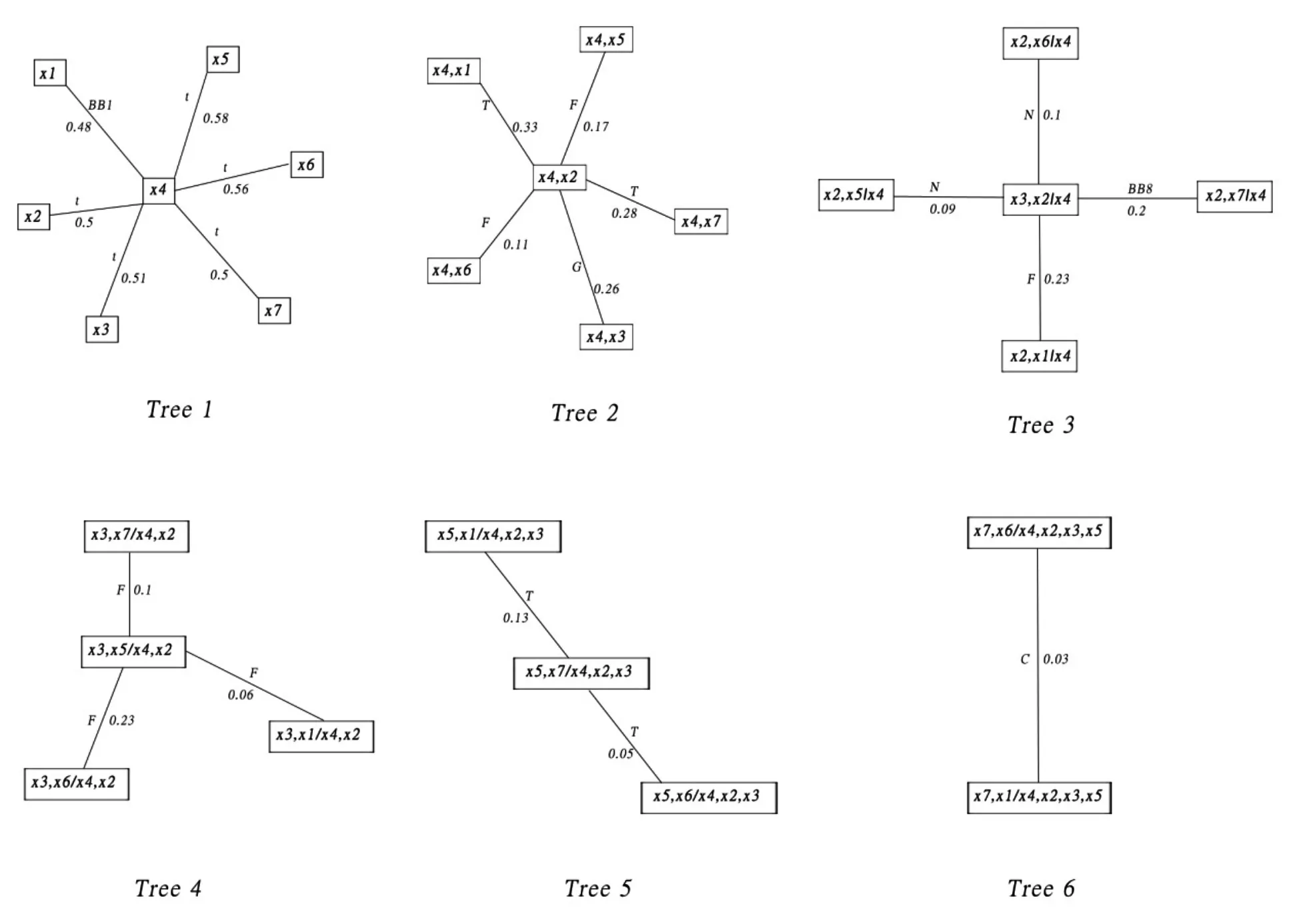
图3 我国银行业系统性风险结构和大小

图3中，两家商业银行之间的字母表示所选用的copula函数的类型，数值表示tau值(也即风险传染的强度)。通过图3，可以清晰看出商业银行业风险传染结构和风险传染强度。该实证结果显示了我国系统性重要商业银行之间的风险传染强度和结构。

具体来看，图3中Tree 1表示了与其他商业银行风险传染总和最大的为商业银行x4。Tree 1 中的连线上的copula表示了两两商业银行之间风险传染，copula的尾部依赖结果表示这种微观商业银行之间的传染结构，tau值表示传染强度的大小。基于该Tree 1的实证结果可以有效实施微观审慎监管：无论是监管机构还是商业银行自身可以根据该图有效了解到商业银行与其他银行之间的风险传染状况，有针对性地通过各种商业银行间的传染渠道来降低风险传染。

Tree 2至 Tree 6主要表示了银行间传染的依赖结构，与Tree 1中类似，tau值表示银行间传染的相依性大小。该数值主要表示了商业银行风险传染的同质性。当该指标的数值较大时，对商业银行的系统性风险将不能仅仅局限在微观审慎监管层面，而应加强宏观审慎监管。

5 结论与建议

本文主要是对基于copula函数金融业系统性风险度量方法的一个拓展。在系统性风险度量中引入C 藤 copula函数，不仅可以度量出系统性风险的大小，而且可以度量出系统性风险中的传染结构。该传染结构区别于条件在险价值和边际风险损失等方法度量出的风险溢出，主要在于该方法不仅度量出了金融机构之间的风险传染，而且利用传染的相依性对传染结构进行了度量。

进一步，本文同样利用C藤 copula函数对我国银行业系统性风险进行了实证分析。通过实证结果，可以发现一些商业银行在系统性风险传染中对其他商业银行传染强度较大。该实证结果度量结果可以对商业银行系统性风险管理和监管提出一些可操作性的建议。首先，根据商业银行风险传染的结构，可以对商业银行实施差异化微观审慎监管。监管部门依照风险传染总强度的次序来对不同的商业银行实施有针对性的监管，如果两家商业银行之间传染强度较大，那么需要对此类商业银行进行风险提示，通过差异化经营、降低业务往来、降低资产互持等多途径来降低商业银行之间的风险传染。其次，根据商业银行风险传染的相依性结构，有针对性地对银行业实施宏观审慎监管。商业银行之间风险传染的相依性增加，那么仅通过微观监管是无法来实现监管目的的，需要宏观审慎监管来降低风险传染的相依性来得到对系统性风险管理的目的。

总体来说，基于copula对系统性风险的度量仍然处于探索阶段。本文基于C 藤 copula对系统性风险的度量主要是从一个静态的视角出发，那么将该方法拓展到动态分析将是接来下研究的一个方向。

[1] Financial Stability Board. Policy Measures to Address Systemically Important Financial Institutions[R]. Basel: Financial Stability Board, 2011.

[2] Bank for International Settlements. Global Systemically Important Banks: Updated Assessment Methodology and the Higher Loss Absorbency Requirement[R]. Basel: Bank for International Settlements,2013.

[3] Benston G J. Federal Regulation of Banking: Historical Overview[R]. Cambridge: Deregulating Financial Services :Public Policy in Flux,1986.

[4] Allen L, Bali T G, Tang Y. Does Systemic Risk in the Financial Sector Predict Future Economic Downturns?[J].Review of Financial Studies,2012,25(10):3000-3036.

[5] Alessi L, Detken C. Quasi Real Time Early Warning Indicators for Costly Asset Price Boom/bust Cycles: A Role for Global Liquidity[J]. European Journal of Political Economy, 2011, 27(3): 520-533.

[6] Adrian T, Brunnermeier K M. CoVaR [R]. Cambridge:National Bureau of Economic Research, 2011.

[7] 谢远涛,蒋涛,杨娟. 基于尾部依赖的保险业系统性风险度量[J]. 系统工程理论实践, 2014, 34(8): 1921-1931.

[8] 蒋涛,吴卫星,王天一,等. 金融业系统性风险度量——基于尾部依赖视角[J]. 系统工程理论实践, 2014, 34(s1): 40-47.

[9] Financial Stability Board. Update of Group of Global Systemically Important Banks (G-SIBS) [R]. Financial Stability Board: Basel, 2012.

[10] Bernanke B. Financial Reform to Address Systemic Risk [R]. Council on Foreign Relations: Washington DC, 2009.

[11] Brunnermeier M.,Pedersen L. Market liquidity and funding liquidity[J]. Review of Financial Studies, 2009,22:2201-2238.

[12] 吴卫星,蒋涛,吴锟. 融资流动性与系统性风险——兼论市场机制能否在流动性危机中起到作用[J].经济学动态,2015(3)：62-70.

[13] Czado C, Schepsmeier U, Min A. Maximum Likelihood Estimation of Mixed C-vines with Application to Exchange Rates[J]. Statistical Modelling, 2012,12(3):229-255.

[14] Patton A J. Modeling Time-varying Exchange Rate Dependence using the Conditional Copula[M]. San Diego: University of California,2001:118-124.

[责任编辑：张永军]

Systemic Risk Structure Measurement in Chinese Banking Sector：Based on The Perspective of Tail Dependence

JIANG Tao1，LI Zheng-xiao2

(1.School of Banking and Finance,University of International Business and Economics, Beijing 100029；2.School of Statistics,Renmin University of China, Beijing 100872,China)

According to the definition of systemic risk, systemic risk can be divided into risk contagions and the dependence of contagions. The Copula function can be used as a new method, which has many excellent properties, to measure the systemic risk. Based on this, the intensity and the structure of risk contagions can be measured by C vine copula. Furthermore, we conduct the empirical study to measure systemic risk in Chinese banking sector based on C vine copula. Based on the empirical results, we proposal using micro prudential supervision to manage risk contagions, as well as macro prudential supervision to manage the dependence of contagions, as the management of banking systemic risk.

systemic risk; risk contagion; contagion structure; C-vine copula

2016-04-24

2016-08-09

对外经济贸易大学国内外联合培养研究生项目(201501)资助。

蒋 涛(1990—)，男，安徽舒城人，对外经济贸易大学金融学院2014级博士研究生，研究方向：风险管理与资产定价；李政宵(1991—)，男，四川成都人，中国人民大学统计学院博士研究生，研究风向：风险模型与精算。

F830

A

2096-2371(2016)04-0017-07