基于灵敏度分析微网孤岛运行下的频率控制器研究

李宁，王大成，张航

（广东石油化工学院机电工程学院，广东茂名 525000）

基于灵敏度分析微网孤岛运行下的频率控制器研究

李宁，王大成，张航

（广东石油化工学院机电工程学院，广东茂名 525000）

以微网孤岛运行时的稳定性分析为目标，将未来可再生电能的传输和管理网络作为研究对象，首先分别推导了固态变压器、网络线路以及负荷模型的状态空间方程，建立了相应环节的小信号模型，并引入了下垂控制器与电压电流双环控制器，建立了完整的微网小信号模型。其次对微网系统状态矩阵进行了特征值的关键性与一般性灵敏度分析，确定了影响系统稳定的环节和系统参数。通过分析结果得出电流环控制器参数对系统稳定性有影响，功率下垂控制器的下垂控制系数对系统稳定性有影响。对微网系统状态矩阵进行了特征值灵敏度分析，该分析方法对微电网系统频率控制器优化配置提供理论支持。

高压微网；固态变压器；小信号模型；孤岛运行；下垂控制

微电网作为分布式电源接入电网的一种有效手段，引起了广泛关注，它是由分布式电源、储能设备及负荷组成的小规模发配电系统[1-3]。其运行特性具有并网和独立模式，具有很高的灵活性，近年来是国内外研究的热点[4-5]。

为解决分布式电源并网并提高其利用效率，微网的概念被提出，与传统大电网相比较，微网距离负荷更近，无需进行超高压远距离送电，从而减少了配电建设投资费用。微网还兼备并网和孤岛两种运行模式，体现了微网“即插即用”的特点。

高压微网模型是一种环形网络，各分布式电源、负载、储能装置通过固态变压器与外网连接，高压环网电压等级为10 kV。当微网孤岛运行时，由于其脱离了大电网，因此失去了大电网的电压和频率的支持，从而导致控制较为复杂，目前多采用下垂控制来实现对电压和频率的控制。分布式电源通过电力电子装置接入环网，这样在提高系统控制灵活性的同时，存在系统惯量小、受扰动易失稳等特点，使得微网孤岛运行时控制变得更为复杂。

以高压环网孤岛运行时的稳定性为分析目标，首先介绍了基于固态变压器（Solid State Transformer，SST）的高压环网模型的具体结构、SST接入环网的等效电路等内容，通过对环网内各个环节状态空间模型的推导，建立了微网小信号模型，并对微网系统状态矩阵进行了特征值和灵敏度分析，最后确定了影响系统稳态运行的环节和参数范围。

1 微网模型

未来可再生能源的传输和管理网络是基于固态变压器的新型高压环形网络。环网模型包括环网和SST的具体结构，然后通过对环网内各环节状态空间模型的推导，最后建立整体微网的小信号模型。

高压环网可实现分布式电源的并网，满足用户双向供用电需求，各分布式电源、储能装置和负荷通过固态变压器的低压交直流母线接入环网系统，如图1所示，这样方能实现供用电设备的即插即用。

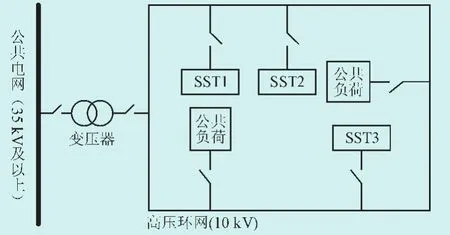
图1 基于SST的高压微网结构Fig.1 The structure of high voltage microgrid based on SST

固态变压器是基于电磁感应原理，将电力电子设备与常规变压器技术相结合的一种新型电力设备。其工作原理为：首先由电力电子装置将原边输入的工频信号变换成高频信号，再通过高频变换单元将信号耦合到变压器的副边，最后由电力电子装置将高频信号变为工频信号。

SST结构如图2所示，主要由高低压变流器和中间的DC-DC变换器组成，以实现固态变压器与环网间功率的双向流动，当低压交直流端需要从环网吸收电能时，高压变流器工作于整流状态，低压变流器工作于逆变状态。相反，当低压交直流端向环网输送电能时，低压变流器工作于整流状态，高压变流器工作于逆变状态。

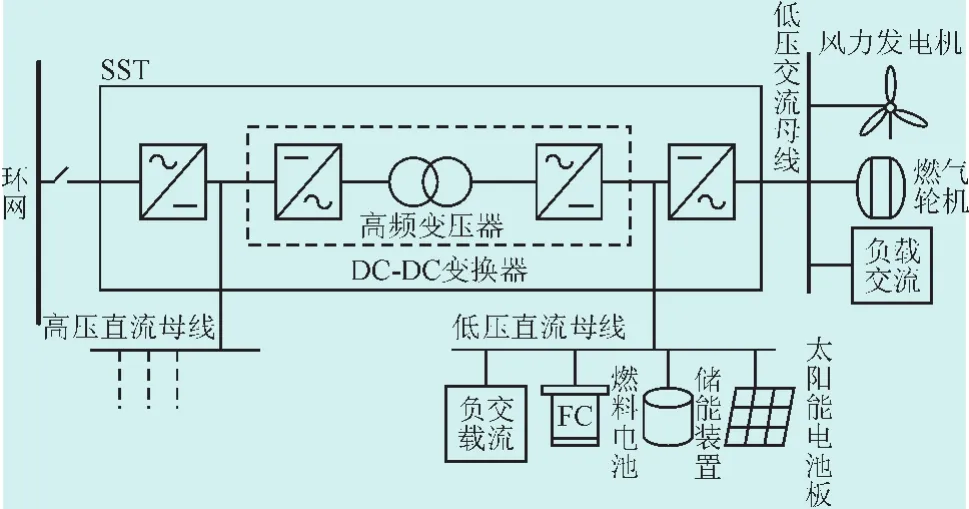
图2 固态变压器（SST）基本结构Fig.2 Basic structure of the solid state transformer（SST）

固态变压器中间的DC-DC变换器由高频变压器、单项全桥逆变器和单相全桥整流器组成，采用PWM控制，中间的高频变压器不仅有电压变换的功能，同时还有电气隔离功能。微网孤岛运行时，环网负载要求分布式电源通过固态变压器升压向其供电，高压变流器处于逆变状态。

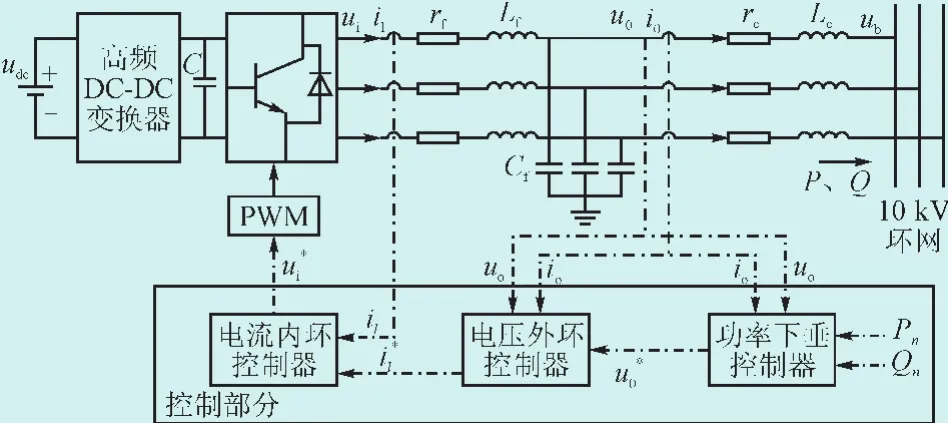
图3 SST接入环网等效电路Fig.3 The equivalent circuit of SST access ring network

系统的数学模型[2]为：

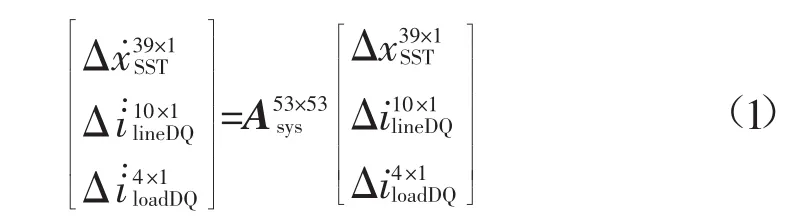
Asys系统状态矩阵表达式：

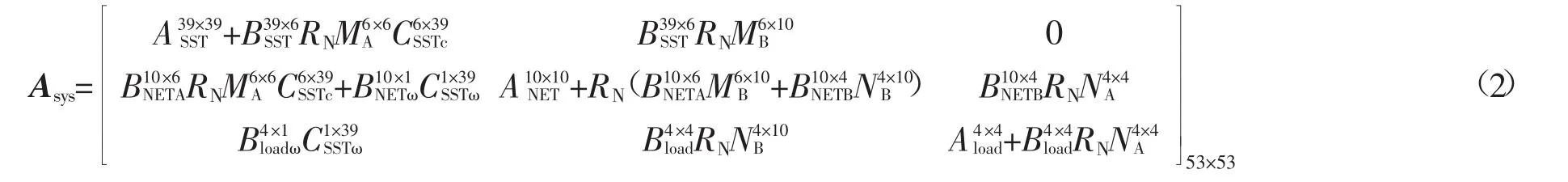
式中：SST下标为SST小信号模型状态变量；line下标为网络线路小信号模型状态变量；load下标为负荷小信号模型状态变量。

2 系统的特征值灵敏度分析

在系统的设计和分析中，确定系统稳定运行是首要任务，需要对系统状态矩阵特征值进行分析，特征值灵敏度分析通过求取系统状态矩阵特征值，计算特征值对状态矩阵元素的灵敏度。

分析状态矩阵特征λi对状态矩阵Asys对角线元素αkk的灵敏度可得到影响系统特征值的状态变量，进而可得到影响系统特征值的系统参数。由于系统状态矩阵特征值数量较大、分布区域较广以及数值接近的特征值对对角线元素的灵敏度较为相近的原因，对特征值灵敏度进行分段计算，并抽取典型分析其对系统的影响。同时，将距离虚轴最近的一对共轭特征值的灵敏度以及下垂控制单元的灵敏度纳为关键因素进行详细分析，将其余特征值作为一般因素进行分析。状态矩阵Asys特征值和特征向量的关系为：

上式对αkj（αkj为状态矩阵Asys中第k行j列的元素）求偏导得：

同时左乘ψiφi，ψi满足ψiφi=1并且ψi（A-λiI）=0两条件，可以将式（4）简化为：

在∂Asys/∂akj中，除了第k行j列的元素等于1以外，其余元素都等于0，因此状态矩阵Asys的特征值对矩阵元素的灵敏度可表示为：

进而可得到特征值对状态矩阵对角线元素的灵敏度：

系统一共包含53个状态变量，见微网系统小信号模型式（2）所示，SST小信号模型包含39个状态变量，网络线路小信号模型包含10个状态变量，负荷小信号模型包含4个状态变量。

3 键特征值灵敏度分析

本次研究的环网额定电压为10 kV，频率50 Hz，环网内包含2个公共负荷和3个SST，微网额定容量1 MW，各分布式电源具备20%的备用容量，线路阻抗根据10 kV典型线路参数计算。

在分析系统稳定性时，对于距离虚轴较近特征值的分析是关键，由于该区域系统特征值阻尼小，所以其变化更容易导致系统不稳定。本节对距离虚轴最近的以及次近的特征值进行了灵敏度分析，得出了能使系统稳定的系统参数范围，并对相应控制环节的控制参数进行了选取。

求取状态矩阵Asys特征值，可以发现特征值全部位于虚轴左半平面，由此可知，微网系统稳定。如图4所示，将分布在距离虚轴最近的特征值区域设为影响区进行分析，将分布在其他区域的特征值设为非影响区进行分析。

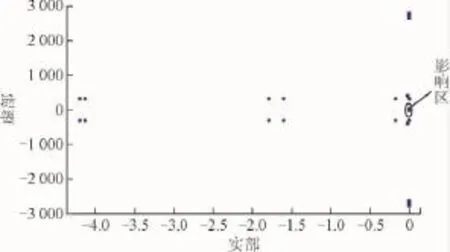
图4 状态矩阵特征值Fig.4 The eigenvalue of state matrix

3.1 距离虚轴最近的特征值灵敏度分析

通过图4得到的特征值可知影响区域中的特征值距离虚轴最近，通过计算得到第47到第52个特征值距离虚轴最近，其中第51和52个特征值共轭，由于这对特征值的分析结果几乎相近，因此以下只对第51个特征值的灵敏度进行具体分析。分析结果如图5所示。

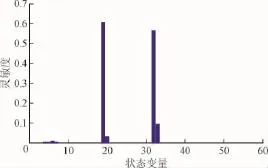
图5 第51特征值灵敏度Fig.5 Fifty-first sensitivity of eigenvalue

由图5知，对系统特征值影响最大的是第6、7、19、20、32、33个状态变量，即电流内环状态变量为Δγd1、Δγq1、Δγd2、Δγq2、Δγd3、Δγq3，具体灵敏度数值见表1。

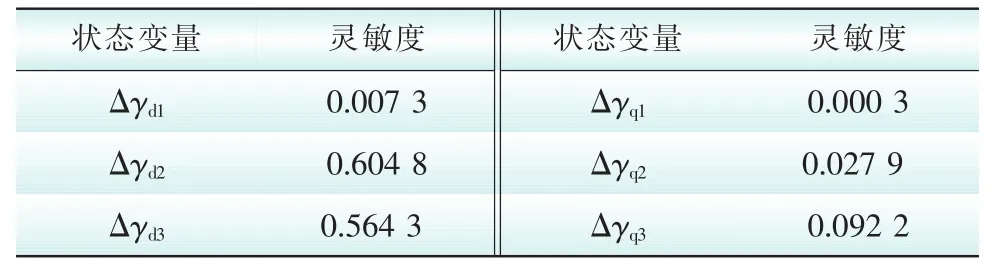
表1 第51个特征值灵敏度Tab.1 The sensitivity of fifty-first eigenvalue

知对应为电流内环状态变量，因此对电流内环PI调节器的比例环节参数Kpc和积分环节参数Kic进行分析。

经分析得到当Kpc从2.069增大到2.069×102时，系统特征值会逐渐趋近虚轴，导致系统不稳定；当积分时间常数Ti（Kic=1/Ti）从1.24减小到1.24×10-6时，系统特征值会逐渐趋近虚轴，导致系统不稳定。由经典控制理论可知，比例系数太大会导致系统失稳，而积分时间常数越大，则积分作用越弱，反之会增强，增大积分时间常数会减慢消除静差的过程，但可减小超调，提高系统稳定性。

由上文选取电流内环PI调节器比例环节参数Kpc=20，积分环节参数Kic=8.04×10-6，能够保证系统的暂态稳定。

3.2 对距离虚轴次近特征值的灵敏度分析

本文中所建立的小信号模型中包含的参数较多，对于系统的影响需要进行多方面因素的考虑，因此有必要对影响区中距离虚轴次近的特征值进行灵敏度分析，以更全面了解影响系统稳定运行的环节和更好地设置系统参数。

对距离虚轴次近的第39-42个特征值进行分析，同上节，选取第42个特征值为研究对象，得到其灵敏度如图6所示。

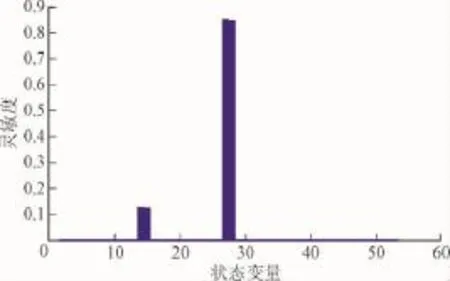
图6 第42特征值灵敏度分析Fig.6 Forty-second sensitivity of eigenvalue sensitivity analysis

由图6知，影响功率下垂控制环节主要是Δδ2、ΔP2、Δδ3、ΔP3的灵敏度较高。具体灵敏度数值见表2，对应为有功功率下垂控制器参数Kp。

表2 第42个特征值灵敏度Tab.2 The eigenvalues of forty-second sensitivity

只有通过控制电压的频率才能控制SST输出电压和并网端电压之间的相位差，从而实现对SST输出有功功率的控制，因此下垂控制系数Kp大小的选取将直接影响SST输出频率的控制。

分析kp1从0.3×10-8变化到0.3×10-5，其他2个SST的下垂控制参数按照功率分配原则成比例进行变化，特征值会逐渐趋近于虚轴，导致系统不稳定。为了能够使系统稳定，所选取的下垂控制参数为kp1= 0.3×10-6。

4 结论

以新型高压环网为研究对象，推导了固态变压器、网络线路以及负荷模型的状态空间方程，建立了微网整体的小信号模型。根据对微网系统进行的特征值和灵敏度分析选择了电流环以及功率下垂控制环节参数，实现了对微网频率的控制，保证了系统的稳定运行。本文对微网系统建立的小信号模型以及通过状态矩阵特征值和灵敏度分析确定控制系统参数的方法对微网稳定性研究有一定的借鉴意义。

本文通过对微网系统的控制结构进行设计，确定了影响系统稳态性的控制参数，并对其进行了分析和矫正，提供了一种控制器参数定量计算的方案。

[1]ZENG Z，YANG H，ZHAO R X，et al．Topologies and control strategies of multi-functional grid-connected inverters for power quality enhancement：A comprehensive review[J]．Renewable and Sustainable Energy Reviews，2013（24）：223-270．

[2]杨新华，雷洋洋，吴丽珍，等.交流型微网指定次电压谐波主动补偿策略[J].电网与清洁能源，2015，31（5）: 21-26.YANG Xinhua，LEI Yangyang，WU Lizhen，et al．Auto-nomous selective voltage harmonics compensation control method in an AC microgirdl[J].Power System and Clean Energy，2015，31（5）:21-26（in Chinese）.

[3]LI Yan，LI Yunwei.Power management of inverter interfaced autonomous microgrid based on virtual frequencyvoltage frame[J].IEEE Trans on Smart Grid，2011，2（1）: 30-40．

[4]PRABHA KUNDUR．Power system stability and control[M].McGraw-Hill Professional，1994：700-825．

[5]HE Jinwei，LI Yunwei.An enhanced microgrid load demand sharing strategy[J].IEEE Tans on Power Electronics，2012，27（9）:3984-3995.

[6]HONG Z J，WANG Y T，WANG Z J，et al.Study on microgrid operation modes switching based on eigenvalue analysis[C]//International Conference on Advanced Power System Automation and Protection.IEEE，2011:445-450.

[7]PAHASA J，NGAMROO I.Coordinated control of wind turbine blade pitch angle and PHEVs using MPCs for load frequency control of microgrid[J].IEEE Systems Journal，2016，10（1）:97-105.

[8]向如意，杨金明.基于小信号模型的永磁直驱风电系统特征值灵敏度分析[J].电网与清洁能源，2015（5）:94-101.XIANG Ruyi，YANG Jinming．Analysis on eigenvalue sensitivity of driven permanent magnet wind power system based on small signal model[J].Power System and Clean Energy，2015（5）:94-101（in Chinese）.

[9]杨永超，向如意.并网型永磁直驱风电系统非线性模型扰动稳定域分析[J].电网与清洁能源，2016（4）:112-118.YANG Yongchao，XIANG Ruyi．Driven permanent magnet wind power system for disturbance stability region based on nonlinear model[J].Power System and Clean Energy，2016（4）:112-118（in Chinese）.

[10]韩强，蒋燕玲，马进．基于STATCOM的双馈风电场无功电压控制的研究[J]．陕西电力，2012（11）：20-25，37．HAN Qiang，JIANG Yanling，MA Jin．Research on reactive power and voltage control in wind farm based on STATCOM and DFIG[J]．Shaanxi Electric Power，2012（11）：20-25，37（in Chinese）.

[11]邵庆华，邵昱，赵波．风速扰动情况下的风电并网电压稳定性研究[J]．陕西电力，2013（3）:15-17，22．SHAO Qinghua，SHAO Yu，ZHAO Bo．Study on voltage stability of regional power grid-connected wind farms under wind disturbance[J]．Shaanxi Electric Power，2013（3）:15-17，22（in Chinese）.

[12]郭涛，秦睿，马呈霞．利用回热抽汽控制参与风电系统调频方法研究[J]．节能技术，2014（2）:108-111．GUO Tao，QIN Rui，MA Chengxia．Frequency regulation method with using steam turbine regenerators in wind power system[J]．Energy Conservation Technology，2014（2）:108-111（in Chinese）.

[13]张赵青，朱建国，王雪．影响风电场电能质量的因素研究[J]．节能技术，2014（6）:516-519．ZHANG Zhaoqing，ZHU Jianguo，WANG Xue．Research on the factors for the quality of wind electric farm power[J]．Energy Conservation Technology，2014（6）:516-519（in Chinese）.

[14]陈达，张玮．风能利用和研究综述[J]．节能技术，2007（4）:339-343，359．CHEN Da，ZHANG Wei．Exploitation and research on wind energy[J]．Energy Conservation Technology，2007（4）: 339-343，359（in Chinese）.

[15]傅旭，李海伟，李冰寒．大规模风电场并网对电网的影响友对策徐述[J]．陕西电力，2010（1）：53-57．FU Xu，LI Haiwei，LI Binghan．Review on influences of large-scale wind farms power systems and countermeasure[J]．Shaanxi Electric Power，2010（1）：53-57（in Chinese）.

（编辑 徐花荣）

Study on the Frequency Controller of Microgrid during Islanded Operation Based on Sensitivity Analysis

LI Ning，WANG Dacheng，ZHANG Hang
（College of Mechanical and Electrical Engineering，Guangdong University of Petrochemical Technology，Maoming 525000，Guangdong，China）

Targeting the stability analysis of microgrid during islanded operation and taking delivery and management of renewable electric energy in future as the research object，this paper，first of all，derives the state space equations of the solid state transformer（SST），network line and load model respectively，and then establishes the small-signal model of the corresponding link，and droop controller，voltage-loop and current-loop controller are introduced to control the voltage and frequency，thus a complete microgrid small-signal model is established.Secondly，the parameters which affect the stability of system are determined according to the key and general eigenvalues and sensitivity of the state matrix analysis.The analysis concludes that both the parameters of the current-loop controller and the droop controller affect the stability of the microgrid system.The eigenvalue value sensitivity analysis is carried out for the state matrix of the micro grid system，providing the theoretical support for the optimal allocation of the frequency controller of the micro grid system.

high-voltage microgrid；solid state transformer；small-signal model；islanded operation；droop control

广东省高等教育学会实验室管理专业委员会基金（GDJ2012068）。

Project Supported by Guangdong Provincial Institute of higher education laboratory management Specialized Committee fund（GDJ2012068）.

1674-3814（2016）10-0109-05

TM712

A

2016-05-20。

李 宁（1976—），男，硕士，实验师，研究方向为频率控制器算法以及设备状态检测与故障诊断。