Riemann-Liouville和Cputo分数阶微积分

周碧波，张润玲，雷 勇

（吕梁学院数学系，山西 吕梁 033000）

Riemann-Liouville和Cputo分数阶微积分

周碧波，张润玲，雷 勇

（吕梁学院数学系，山西 吕梁 033000）

利用伽马函数无穷积分探讨了从整数阶微积分到分数阶微积分的过渡和演绎.通过证明整数阶微积分仅是分数阶微积分的一种特殊情况，拓宽了导数和积分的概念.阐述了Riemann-Liouville和Cputo两种不同分数阶导数定义的区别和联系，给出了Hadamard积分与Riemann-Liouville导数之间的关系.

整数阶微积分；分数阶微积分；伽马函数；Hadamard积分

牛顿和莱布尼茨创立的微积分是变量数学时期最主要的科学成就，微积分的诞生是全部科学史上，也是人类历史上最伟大最有影响的创举.分数阶微积分最早由著名数学家Hospital于1695年提出：

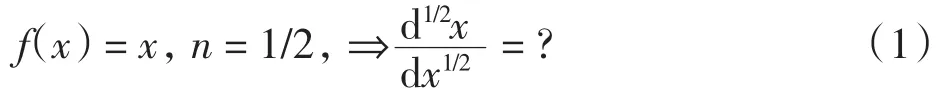
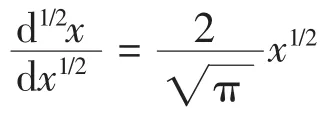
耶鲁大学教授Manderbrot指出：自然界和科学界存在大量的分数维.分数阶微积分已成为研究分数阶微分方程、分形函数等的有力工具，被广泛应用于分形几何、分形函数、分形偏微分方程、函数空间等领域的研究[1-4]，分数阶在量子力学、化学物理、流体学、电力网络、粘弹性、医学等众多领域也有着广泛的应用[5-6].

1 分数阶导数和积分

引理 变上限函数积分具有如下性质：

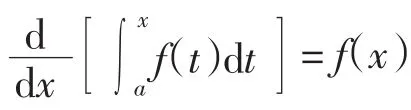
由引理可得

由此不难推出n阶整数阶变上限函数的导数公式

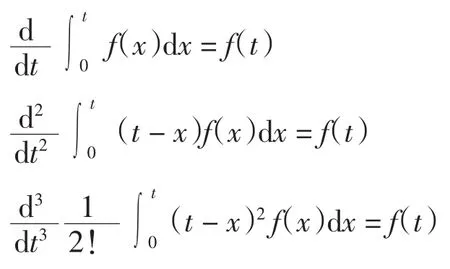
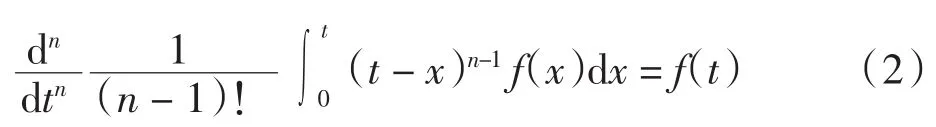
由于整数阶导数和积分在不考虑常数的情况下是互逆运算，对式（2）两边同时求n阶积分，再由伽马函数性质可得

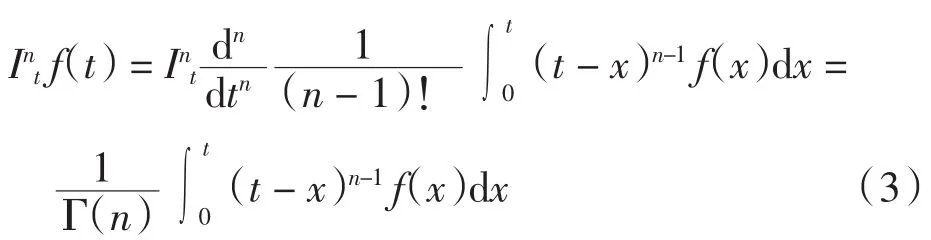
定义1[8]（Riemann-Liouville分数阶积分） 若函数f（t）连续，则f（t）的α次积分为

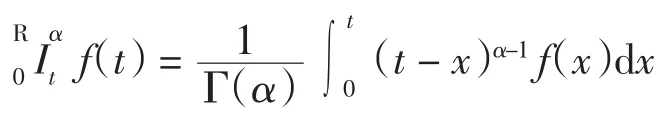
其中：α>0，t>0，f∈L′[0，t].

定义2[9]（Riemann-Liouville分数阶导数） 设函数f（t）连续，当0<α<1时，f（t）的α次导数为

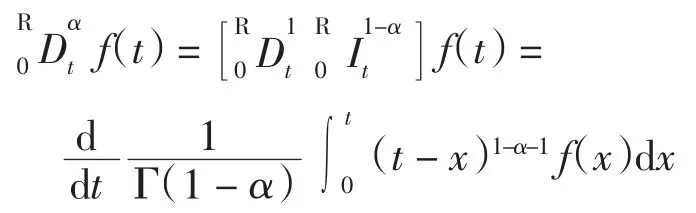
当n-1<α≤n时，则有

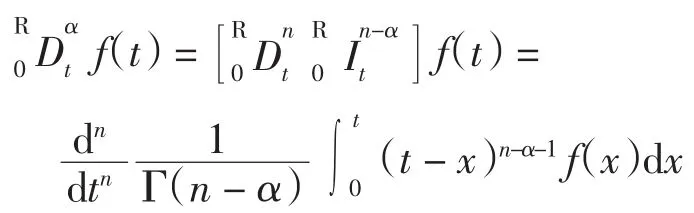
在引入分数阶导数以后，整数阶导数就成为分数阶导数的特殊情况，下面以幂函数为例来说明.

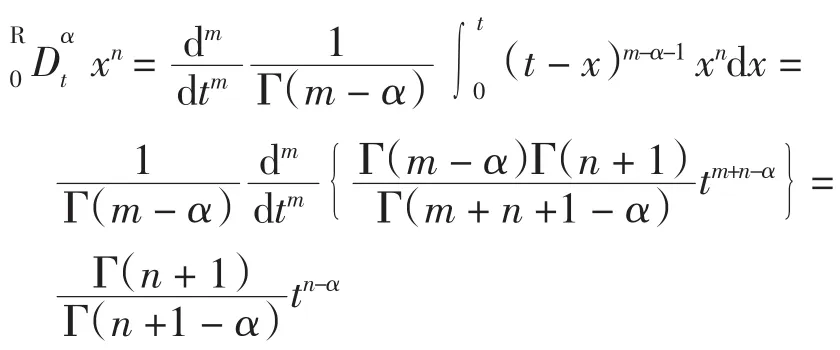
其中m-1<α≤m.当α取整数时结论与整数阶导数结论完全吻合，但是由于Riemann-Liouville分数阶导数具有超奇异性，不便于工程和物理建模中的应用，意大利地球物理学家Cputo提出了弱奇异的分数阶导数，该导数定义解决了分数阶微积分中分数阶初值问题.

定义3[9]（Cputo分数阶导数） 设n-1<α≤n，函数f（t）n阶可导，则f（t）的α次Cputo导数为

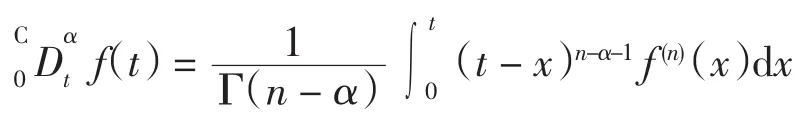
由以上定义可以看出，Riemann-Liouville分数阶导数和Cputo分数阶导数定义的区别在于积分和求导的顺序不同，Riemann-Liouville分数阶导数是先积分再求导，而Cputo分数阶导数是先求导后积分，从数学的角度上来说，Cputo分数阶导数定义的要求更高一些，它要求函数具有n阶导数.Cputo方法的主要优势是使分数阶微分方程的初始条件可以采用和整数阶微分方程相同的形式.

另外，在分数阶导数微分方程数值计算中经常需要构造差分格式，为了方便计算，经常把Riemann-Liouville分数阶导数中的积分部分转化为Hadamard积分，现给出Hadamard积分定义.

定义4[7]（Hadamard积分） 设g（w）足够光滑，0< α≤1，g（w）的Hadamard积分为

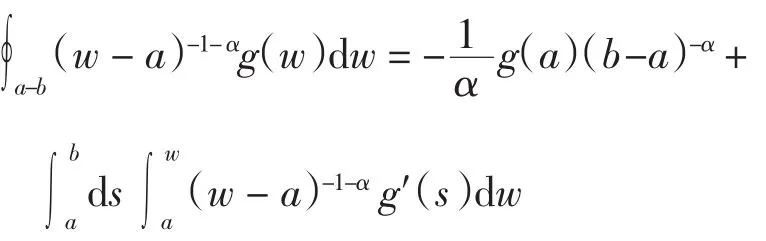
其中：a-b表示积分的上限和下限，a为积分下限，b为积分上限.

2 几个相关结论

定理1 令f（t）=（t-a）k，设α>0，k>-1，则有

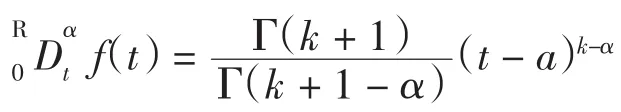
证明 由Riemann-Liouville分数阶导数定义有

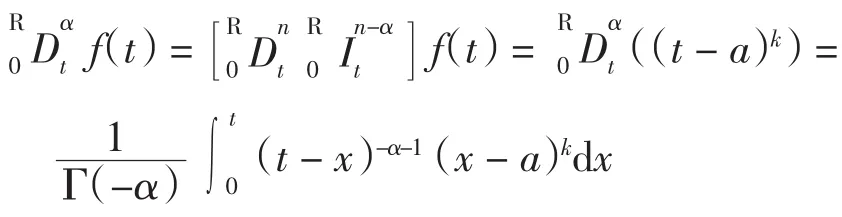
令x=a+u（t-a），则有

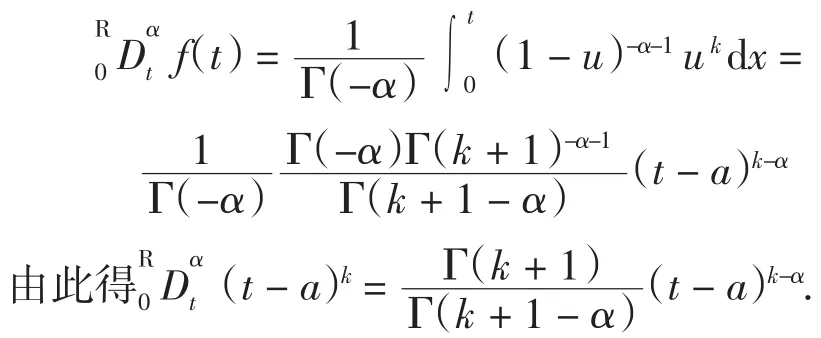
定理2 设f（t）、g（t）为两个函数，λ、μ为常数，则有

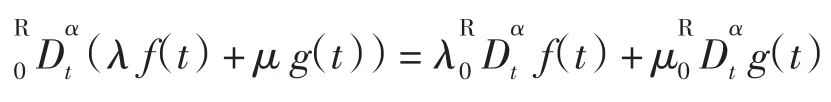
证明 由条件可得

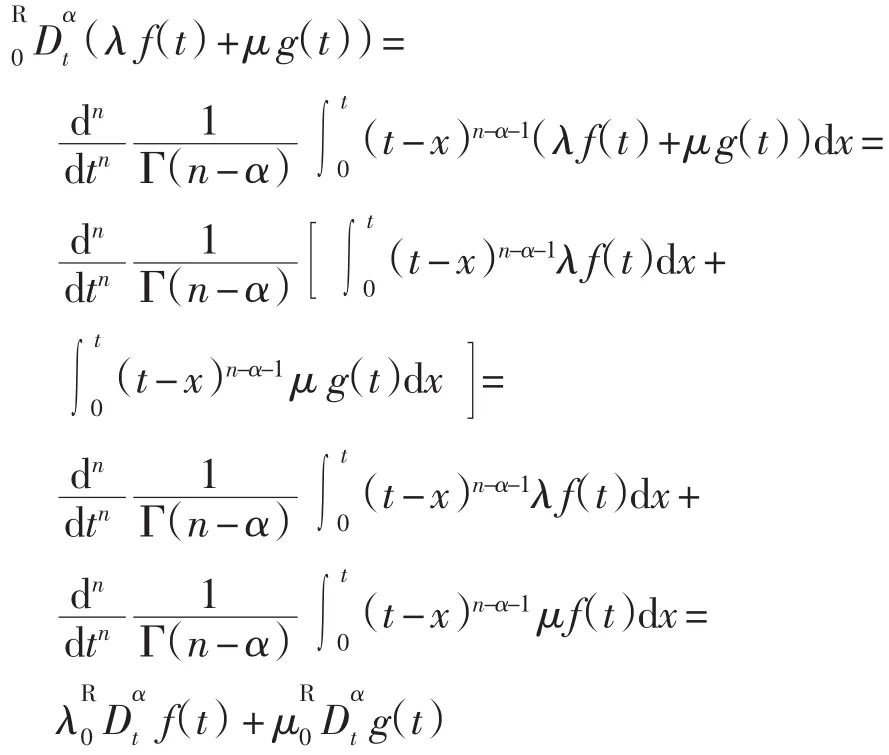
定理3 当0<α≤1时，Riemann-Liouville分数阶导数和Hadamard积分有如下关系

其中

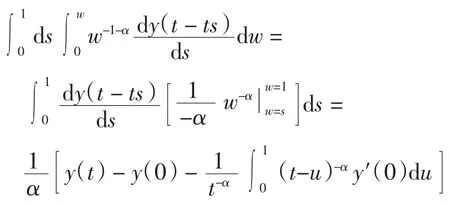
定理3给出了当0<α≤1时，Riemann-Liouville分数阶导数和Hadamard积分之间的关系，这个关系式对于微分方程构造差分格式计算近似值具有非常重要的意义，若m-1<α≤m，依然可以利用Hadamard积分定义和泰勒公式得到类似的Riemann-Liouville分数阶导数展开式.

[1]ZHAI C B，YAN W P，YANG C.A sum operator method for the existence and uniqueness of positive solutions to Riemann-Liouville fractional differential equation boundary value problems[J].Communications in Nonlinear Science and Numerical Simulation，2013，18（1）：858-866.

[2]WANG G T，LIU S Y.BELEANU D，et al.A new impulsive multi-orders fractional differential equation involving multi-point fractional integral boundary condition[J].Abstract and Applied Analysis，2014，DOI：10.1155/2014/932747.

[3]FECKA M，ZHOU Y，WANG J.On the concept existence of solution for impulsive fractional differential equations[J].Communications in Nonlinear Science and Numerical Simulation，2012，17（7）：3050-3060.

[4]ZHOU Y，JIAO F，LI J.Existence and uniqueness for type fractional neutral differential equations[J].Nonlinear Analysis：Theory，Methods and Applications，2009，71（7）：2724-2731.

[5]ZHANG X M，ZHANG M.On the concept of general solution for impulsive differential equations of fractional order[J].Applied Mathematics and Computation，2015（268）：103-120.

[6]常福宣，吴吉春，薛禹群，等.考虑时空相关的分数阶对流-弥散方程及其解[J].水动力学研究与进展，2005，20（3）：34-38. CHANG F X，WU J C，XUE Y Q，et al.The fractional order advection dispersion equation with temporal and spatial correlation and its solution[J].Journal of Hydrodynamics，2005，20（3）：34-38（in Chinese）.

[7]LAKSHMIKANTHAM V.Theory of fractional differential equations[J]. Nonlinear Analysis，2008，69（8）：2677-2682.

[8]LIANG S H，ZHANG J H.Positive solutions for boundary value problems of nonlinear fractional differential equation[J].Nonlinear Analysis, 2009，71（11）：5545-5550.

[9]KIBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and ApplicationofFractionalDifferentialEquations[M].Amsterdam：Elsevier，2006.

（责任编校 马新光）

Fractional order differential and integral of Riemann-Liouville and Cputo

ZHOU Bibo，ZHANG Runling，LEI Yong
（Department of Mathematics，Lvliang University，Lvliang 033000，Shanxi Province，China）

The transition from the integer order differential and integral calculus to the fractional order calculus is discussed by using the gamma function infinite integral.It is proved that the fractional calculus is just a special case of fractional order calculus，and the concept of derivative and integral is broadened.The difference and contact of Riemann Liouville and Cputo fractional derivatives are expounded，and the relation between Hadamard integral and Riemann Liouville derivative is given. Keywords：integer order differential and integral；fractional order differential and integral；gamma function；Hadamard integral

O175

A

1671-1114（2016）05-0020-03

2016-03-02

吕梁学院自然科学青年基金资助项目（ZRXY201306，ZRXY201308）.

周碧波（1978—），男，讲师，主要从事非线性泛函分析方面的研究.

张润玲（1966—），女，副教授，主要从事非线性泛函分析方面的研究.