Smith-Toda谱同伦群中的非平凡元素

刘艳芳，王俊丽，王玉玉

（天津师范大学数学科学学院，天津 300387）

Smith-Toda谱同伦群中的非平凡元素

刘艳芳，王俊丽，王玉玉

（天津师范大学数学科学学院，天津 300387）

考虑V（1）谱的同伦群.首先借助May谱序列得到V（2）谱的上同调群的一些结论，然后用代数方法证明了在Adams谱序列中，是永久循环且不是dr边缘,从而收敛到中的非零元.

Smith-Toda谱；Ext群；Adams谱序列；May谱序列；稳定同伦群

球面稳定同伦群是代数拓扑中的一个重要研究课题，Smith-Toda谱V（n）的同伦群与球面稳定同伦群有极其紧密的联系.Adams谱序列是计算球面稳定同伦群的一个重要工具[1]，其E2项其中为模p的Steenrod代数A的上同调（p≥2），它在Cup积下是一个分次代数，Adams微分为

Smith-Toda谱V（n）的Zp上同调群为H*V（n）≅E[Q0，Q1，…，Qn]，其中Qi（i=0，1，…，n）是mod p Steenrod代数A的Minlor基元，E[]是外代数.由文献[6-8]知，当 n=0，1，2，3且p＞2n时，V（n）可实现.由上纤维序列

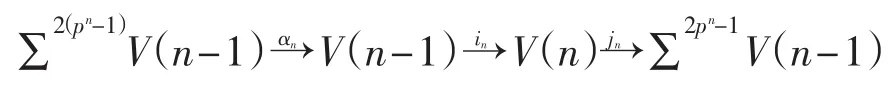
可导出短的Zp上同调群的正合序列，进一步导出如下

Ext群长正合序列

其中V（-1）=S，当n=0，1，2，3时，αn分别为p，α，β，γ.

当t-s＜（p3+3p2+2p+1）q-4时，文献[9]得到Hs，t（U（L））由以下上同调类（乘法）生成

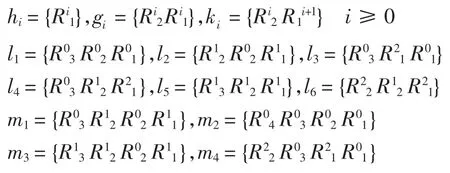
关于加法有

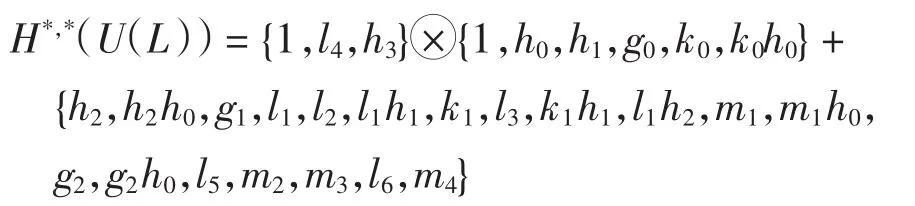
本研究考虑V（1）谱的同伦群，首先借助May谱序列得到V（2）谱的上同调群的一些结论，然后利用Adams谱序列作为工具，证明了如下结论.

以下记全次数为|*|，记第二次数为Sdim.

1 Ext群的相关结论

命题1[10]，其中t-s＜ 2p4-1.

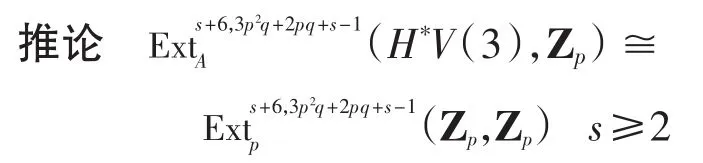
证明 由推论知

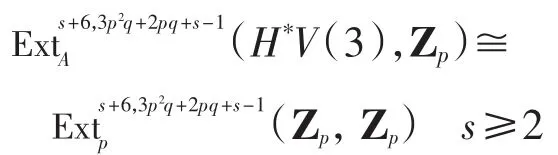
表1 生成元λ及其全次数|λ|（mod pq-2）Tab.1 Generator λ and its degree|λ|（mod pq-2）

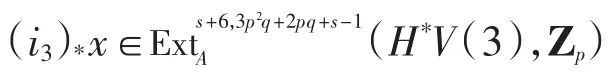
此时（i3）*x的全次数为Q=3p2q+2pq-7=3q+3（mod pq-2）.由表1可知，x可能为其相应的全次数分别为2p2q+2pq+q-5、p2q+3pq+ 2q-5，均与（i3）*x的全次数3p2q+2pq-7不等，故（i3）*x=0.

考虑如下长正合序列

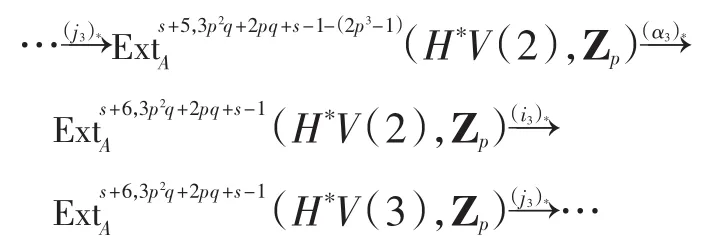
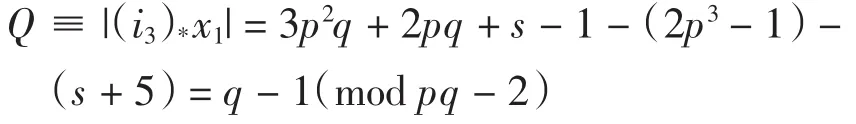
由表1可知x1可能为h0，其相应的全次数与（i3）*x的全次数不等，故

重复上述做法，x1=（α3）*x2其中

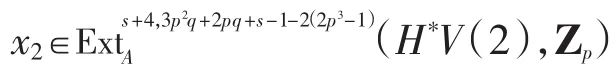
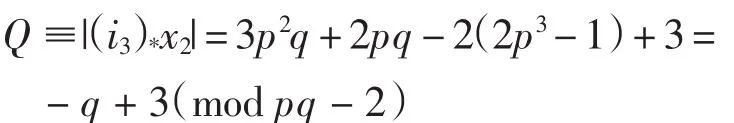
由表1知x2不存在，故（i3）*x2=0.

同理 x2=（α3）*x3，其中（H*V（2），Zp）=0，满足x2=（α3）*x3=0.因此可得x=（α3）*（α3）*（α3）*x3=0，即

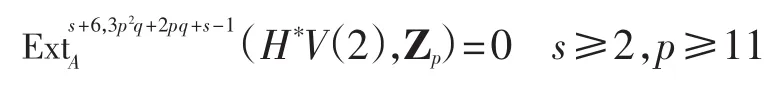
证明 当r≥6时，命题显然成立.下面考虑2≤r≤5的情形.

Sdim（（i3）*y）=3p2q+2pq+1-r≡q+1-r≠0（modq）且当t≠0（mod q）时，Extr，tp（Zp，Zp）=0，由命题1得

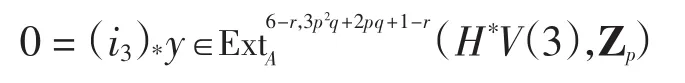
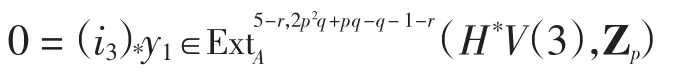
同理（α3）*y3=y2，其中Zp）=0.由|y3|＜0，故有y=（α3）*（α3）*（α3）*y3=0.

2 定理的证明

引理1 当p≥11，s≥2时，有

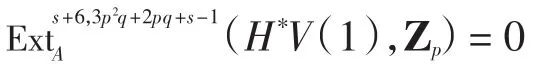
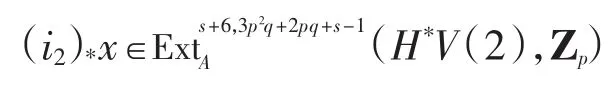
则由长正合序列

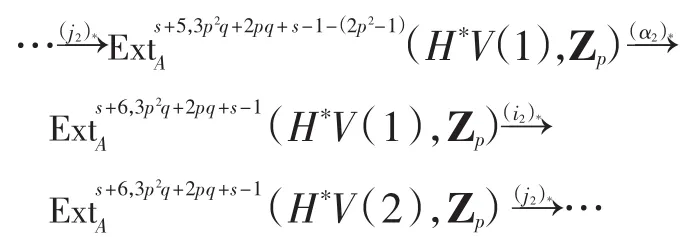
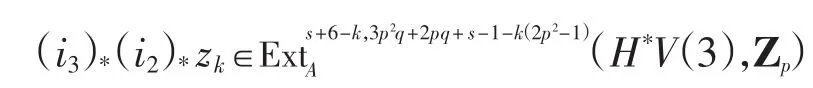
此时

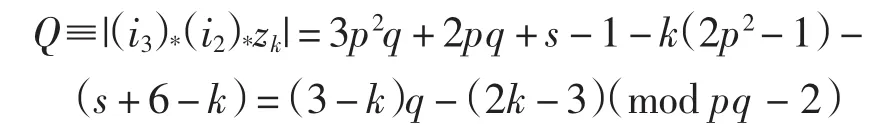
（1）当k=1，2，3时，

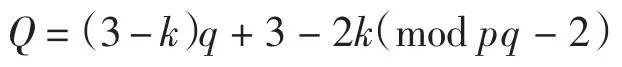
当k=2时，Q=q-1（mod pq-2）.此时λ可能为h0，满足|λ|=q-1（mod pq-2），其全次数为q-1，与（i3）*（i2）*zk的全次数不相等，故（i3）*（i2）*zk=0.

当k=3时，Q=-3（mod pq-2）.由表1可得,无元满足Q=-3（mod pq-2），故（i3）*（i2）*zk=0.

（2）当3＜k＜p-5时，Q=（3+p-k）q-2k-1（modpq-2）或Q=（2+p-k）q+（q-2k+1）（mod pq-2），分别满足

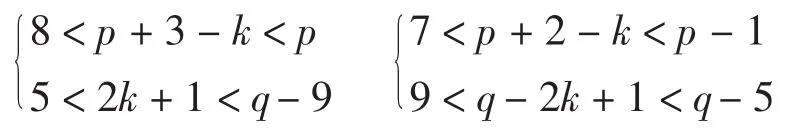
前者显然无对应元.对于后者，由于Q=3p2q+2pq-2kp2-7+2k（k≥1），故在满足|λ|=（2+p-k）q+（q-2k+1）（modpq-2）的λ中，若含有因子或，则与的个数和最大为3.由表1知|λ|=aq+b（mod pq-2），其中a最大为8，若2+p-k=8，则q-2k+1=11，显然满足|λ|=8q+11（mod pq-2）的λ也不存在，即在这种情况下也无对应元.

（3）当k=p-5+s时，Q=（7-s）q+（9-2s）（mod pq-2），其中s=0，1，…，7，满足表1的可能生成元μ及其全次数|μ|见表2.

表2 生成元μ及其全次数|μ|Tab.2 Generator μ and its degree|μ|

当s=0，1，…，7时，（i3）*（i2）*zk的全次数为Q= 3p2q+2pq-2（p-5-s）p2+2（p-5+s）-7，与表2中对应的全次数|μ|均不相等,故此情况下无对应元.

（4）当p+2＜k＜2p-6时，Q=（2+2p-k）q-（2k+ 1-q）（mod pq-2）或Q=（1+2p-k）q+（2q-2k-1）（mod pq-2），分别满足

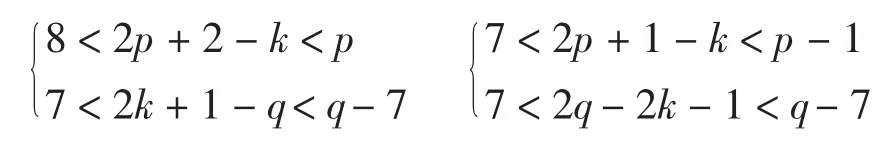
类似于（2）的讨论，此时无对应元.

（5）当k=2p-6+s时，其中s=0，1，…，7，Q=（7-s）q+（7-2s）（mod pq-2），类似于（3）的讨论，此时无对应元.

（6）当2p+1＜k＜3p-7时，Q=（1+3p-k）q-（2k+ 1-2q）（mod pq-2）或Q=（3p-k）q+（3q-2k-3）（mod pq-2），分别满足

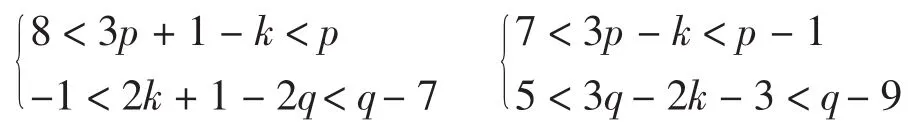
类似于（2）的讨论,此时无对应元.

（7）当k=3p-7+s时，其中s=0，1，…，7，Q=（7-s）q+（5-2s）（mod pq-2），类似于（3）的讨论，此时无对应元.

综上可得

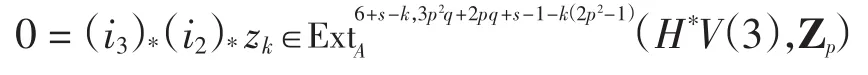
由正合性知存在x4满足（α3）*x4=（i2）*zk，另外，

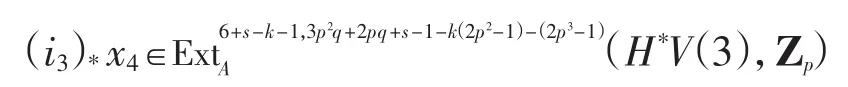
其全次数为

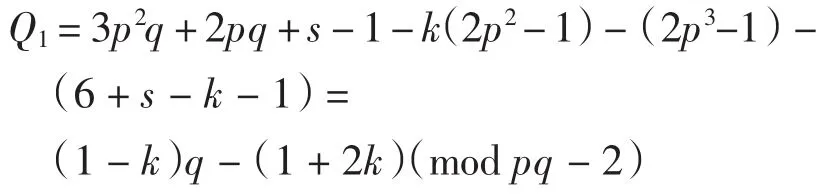
类似于以上对Q的讨论，有

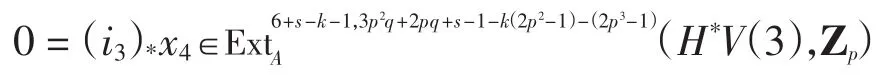
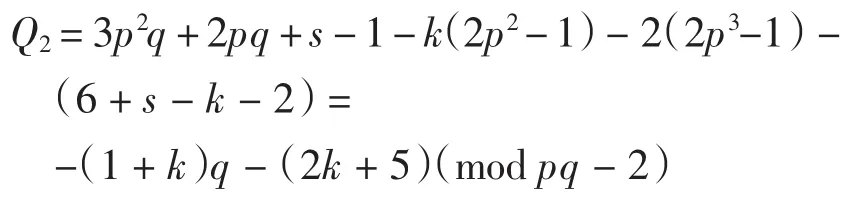
类似于以上对Q的讨论，仍有

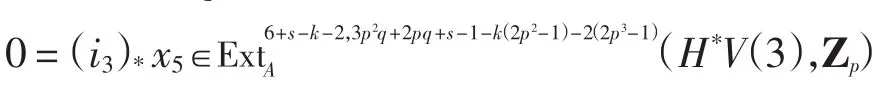
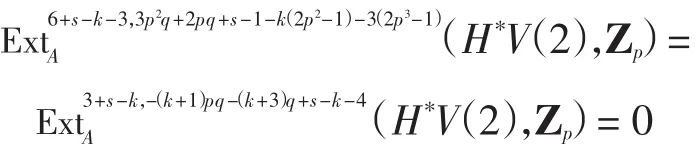
所以x6=0，故x4=（α3）*（α3）*x6=0，即（i2）*zk=（α2）*x4= 0.因此，存在

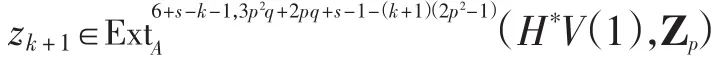
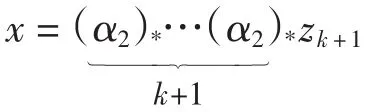
引理2 当p≥11，r≥2时，有

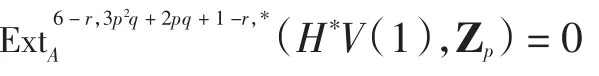
证明 当r≥6时，命题显然成立.下面考虑2≤r≤5的情形.

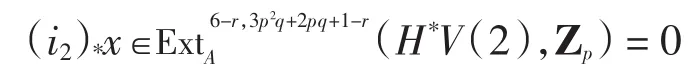
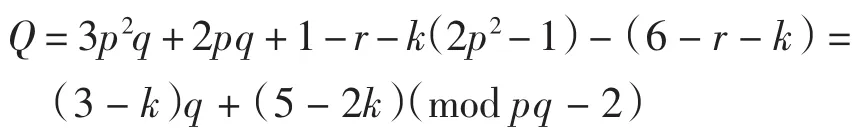
当k=1时，Q=2q+3（mod pq-2）.由表1可知λ可能为，满足|λ|=2q+3（mod pq-2），其相应全次数为2p2q+2pq-3，而（i3）*（i2）*xk的全次数为3p2q+ 2pq-q-5，二者不相等，故（i3）*（i2）*xk=0.

当k=2时，Q=q+1（mod pq-2）.由表1可知λ可能为h2、（b11）h1，满足|λ|=q+1（mod pq-2），其相应全次数分别为p2q-1、2p2q-3，而（i3）*（i2）*xk的全次数为Q=3p2q-2q-5，二者不相等，故（i3）*（i2）*xk=0.

当k=3、4时，Q=-1，-q-3（mod pq-2），由表1可知无对应元，故可得

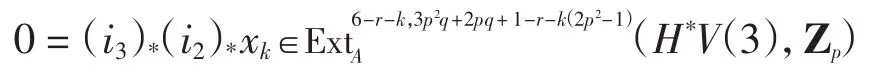
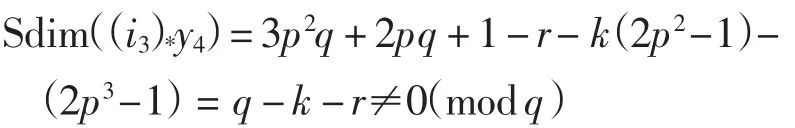
A nontrivial element in homotopy group of Smith-Toda spectrum

LIU Yanfang，WANG Junli，WANG Yuyu
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

The homotopy group of spectrum V（1）is considered，some conclusions about cohomolopy group of spectrum V（2）are obtained by using May spectral sequences.And then it is proved thatis a permanent cycle and can't be hit by any differential in the Adams spectral sequence by using algebra method，this is to say it converges to a notrivial homotopy element in π3p2q+2pq-6V（1）.

Smith-Toda spectrum；Ext group；Adams spectral sequence；May spectral sequence；stable homotopy group

O189.23

A

1671-1114（2016）05-0005-04

2016-01-10

国家自然科学基金资助项目（11301386）.

刘艳芳（1991—），男，硕士研究生.

王玉玉（1979—），女，教授，主要从事球面稳定同伦群方面的研究.