CFRP/GFRP混杂纤维锚杆作用机理及设计理论探讨

朱蓝燕,章雪峰

(1.浙江工业大学建筑工程学院,浙江 杭州 310014；2.浙江工业大学工程设计集团有限公司,浙江 杭州 310014)



CFRP/GFRP混杂纤维锚杆作用机理及设计理论探讨

朱蓝燕1,章雪峰2

(1.浙江工业大学建筑工程学院,浙江 杭州 310014；2.浙江工业大学工程设计集团有限公司,浙江 杭州 310014)

CFRP/GFRP混杂锚杆是旨在利用CFRP良好强度特性和GFRP经济性的一种组合锚杆,如何确定合适的配合比例是混杂纤维锚杆设计的一个重要内容。今根据混杂锚杆的受力性能和锚杆的极限平衡状态得出了不同的承载力理论计算表达式,并与锚杆的受力破坏实验结果进行了比较分析,进而提出了以临界混杂比分阶段计算锚杆承载力的方法。同时,借助BURGERS模型,从理论上分析了碳纤维含量对锚杆蠕变性能的影响。理论分析结果表明：在拉伸强度计算时不能忽略基体的影响；碳纤维的加入能明显提高GFRP锚杆的强度以及改善其蠕变性能,并且可提高锚杆材料的强度利用率；当CFRP含量在0.08～0.30之间时,CFRP/GFRP混杂纤维锚杆具有良好的强度特性和蠕变特性。

单向复合材料板模型；CFRP/GFRP混杂锚杆；BURGERS模型；蠕变性能

混杂纤维复合材料(HFRP)是指由两种或两种以上的纤维增强同一种树脂基体复合而成。HFRP不仅极大扩展了复合材料的性能和使用范围,使材料充分保留单种材料的优点,同时又能弥补单一复合材料的不足,并降低材料成本[1-2]。目前，工程应用的FRP材料主要有GFRP、CFRP、AFRP和BFRP等。不同纤维材料之间可采用不同的方式进行混杂,目前较常用的混杂方式有层间混杂、层内混杂、夹芯混杂三种[3]。GFRP延伸率高而强度和模量低,价格便宜,是目前应用最广的一种纤维,但其单一复合材料使用效果欠佳；CFRP模量和强度高而延伸率低且蠕变性能优良,但价格较高,致使其使用受到限制[4]。由GFRP材料制成的锚杆韧性不好易脆断,在锚杆长期使用过程中易发生蠕变,造成预应力损失,降低锚杆长期耐久性；然而，在GFRP锚杆中混杂CFRP材料能有效提高锚杆强度并改善其蠕变性能,同时提高锚杆材料的强度利用率。

现有文献对HFRP锚杆性能设计理论探讨极少,尤其对其蠕变性能的探讨几乎为空白。本文试图将GFRP和CFRP两种复合材料混杂得到CFRP/GFRP锚杆,并从强度特性和蠕变特性两个角度出发,从理论上探讨CFRP/GFRP锚杆的拉伸和蠕变性能。为CFRP/GFRP锚杆强度及蠕变性能研究作点探索性工作,也可为此类锚杆设计提供理论依据。

1 CFRP/GFRP锚杆材料

CFRP/GFRP锚杆由CFRP和GFRP混杂制成。CFRP/GFRP锚杆由纤维和树脂基体复合而成,基体选用环氧树脂基体。CFRP筋和GFRP筋及基体的基本物理力学性能指标见表1。本研究锚杆材料中纤维所占比例为75%,基体所占比例为25%。

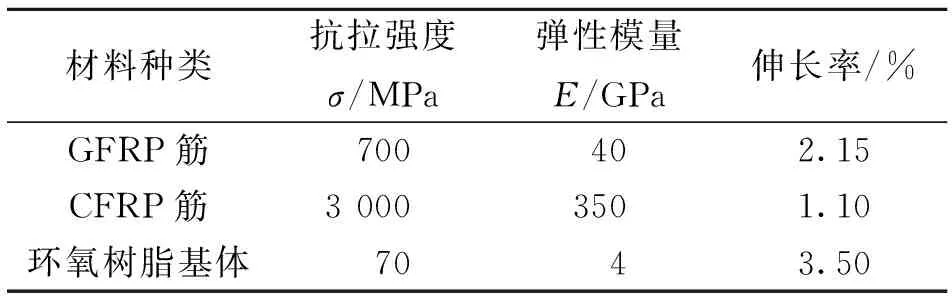
表1 纤维筋基本物理力学性能指标

2 CFRP/GFRP锚杆的强度性能分析

2.1 拉伸性能

为探讨不同碳纤维含量对锚杆性能的影响,作出如下计算假设：

1)碳纤维与玻璃纤维同时达到强度；

2)各种纤维在锚杆件内是均匀分布的。

由假设1)、2),当不考虑基体的强度时,混杂后锚杆极限强度按一般的组合材料方法可简化为：

fu=(σgAg+σcAc)/A

(1)

式中：σg、σc分别为GFRP、CFRP抗拉强度;Ag、Ac分别为GFRP、CFRP所占面积;A为锚杆截面积。

以直径为20 mm的锚杆为例,计算各种配比下CFRP/GFRP锚杆的极限荷载和极限抗拉强度,拉伸强度与碳纤维含量的关系见图1。

混杂纤维复合材料在正常受力时,基体首先因破坏而剥落,且基体的破坏对强度的影响很小,然后低延伸率的纤维材料先发生断裂,由高延伸率的纤维材料继续承载,直到混杂纤维复合材料整体发生破坏[3]。文献[5]将混杂纤维锚杆的受力模型简化成为单向复合材料板模型[6],而单向复合材料板模型的假设条件为：混杂纤维复合材料在受力时,延伸率低的纤维层(如碳纤维)先发生断裂,荷载由剩下的纤维和基体承担,然后延伸率高的纤维层(如玻璃纤维)发生断裂。

借鉴其计算方法,将CFRP/GFRP锚杆的拉伸强度理论计算也简化为单向复合材料板问题。由临界混杂比(混杂比：各纤维相对体积分数之比,一般用CFRP/GFRP中碳纤维含量表示)公式：

(2)

式中：γ为临界混杂比;Ec、Eg、Em分别为CFRP、GFRP、基体弹性模量；σc、σg分别为CFRP、GFRP抗拉强度；λ=(1-Vf)/Vf,λ为基体纤维含量比,其中Vf为纤维含量。

将表1中的数据代入得：γ=0.08,因此,为了达到同时破坏的假设条件,CFRP含量为0.08。当CFRP含量小于0.08时,CFRP先破坏,由GFRP继续承载；当CFRP含量大于0.08时,则混杂纤维锚杆强度主要由CFRP控制。

当Vc<γ时,混杂纤维复合材料拉伸强度为：

(3)

当Vc>γ时,混杂纤维复合材料拉伸强度为：

(4)

根据式(3)和(4)计算CFRP/GFRP混杂复合材料的拉伸强度理论值,拉伸强度与碳纤维含量关系见图1。

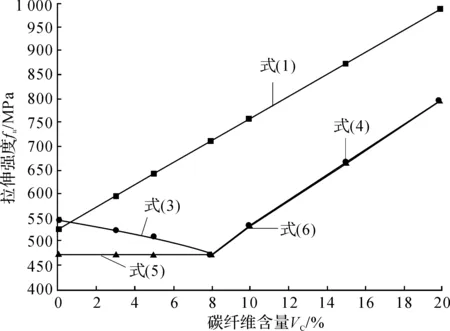
图1 不同碳纤维含量拉伸强度曲线

由图1可知,利用式(1)计算得到的拉伸强度理论值与碳纤维相对含量呈线性关系,随着碳纤维含量的不断增加,拉伸强度不断升高。利用单向复合材料板模型计算得到的拉伸强度理论值随碳纤维含量的增加先下降然后再线性上升,拐点的位置是临界混杂比点。因此,要想获得理想的拉伸强度,碳纤维含量应大于临界混杂比γ。

造成上述两种理论强度计算方法得出的结论不同的原因是，利用式(1)进行理论计算时忽略了基体的影响,而只考虑了两种纤维对锚杆强度贡献的简单叠加;因此，按比例分配两种纤维含量时,随碳纤维含量增加,拉伸强度呈现逐渐上升的线性趋势。而利用单向复合材料板模型,即式(3)和式(4)进行计算时,并未忽略基体的影响。从图1中也可看出,利用式(1)计算得到的拉伸强度与单向复合材料板模型得到的拉伸强度之间相差17%左右。造成两种计算方法不同的根本原因是两者的基本假设不同,前者认为两种纤维同时达到破坏强度,而后者则认为延伸率低的纤维先达到强度而破坏,最终强度由延伸率决定。由于基体强度相对较低,因而对强度的贡献较小,它的存在主要是有利于纤维间的协调工作,提高锚杆的整体强度,因而,基体的影响不能忽略。

由于利用式(1)进行强度计算时直接忽略了基体的影响,利用单向板复合材料模型计算时虽然考虑了基体的影响,但公式冗杂且按式(3)计算时随碳纤维增加导致强度下降,显然是不合理的。因此，两种计算方法都存在一定缺陷。文献[5]将混杂纤维强度的实验结果与理论值进行对比,发现实验数据得到的拉伸强度曲线并未出现临界拐点(即两种纤维同时达到破坏强度的点),由此可以说明纤维混杂后无法达到同时破坏,但两种纤维在基体的作用下相互影响,基本符合单向复合材料板模型所作的假设。于是,将式(1)进行修正,可将CFRP/GFRP锚杆极限拉伸强度理论计算公式表达为

(5)

(6)

式中:σg、σc、σm分别为GFRP、CFRP、基体的抗拉强度；Ag、Ac、Am分别为GFRP、CFRP、基体所占面积；fγ为临界混杂比时混杂纤维锚杆的强度,fγ=470.4 MPa；α为GFRP影响系数,α=0.467；β为CFRP影响系数,β=0.997。

由文献[5]中混杂纤维实验数据可知,在临界混杂比之前,混杂纤维强度没有下降甚至趋于稳定,于是在临界混杂比前修正公式为fu=fγ；在临界混杂比之后,将公式修正为fu=(ασgAg+βσcAc+σmAm)/A形式,根据图1中式(4)所得强度曲线,将每个碳纤维含量所对应的强度代入到上述修正公式中,得到若干组含α、β系数的二元一次方程,再利用MATLAB软件对所得的二元一次方程组进行数值分析求解,得到α、β的值。

利用修正后的强度公式对锚杆进行配比计算,得到修正后的拉伸强度曲线,见图1。

2.2 CFRP/GFRP锚杆的蠕变性能

现有文献关于混杂纤维锚杆蠕变性能方面的研究几乎为空白,但锚杆在长期荷载作用下会产生变形,影响锚杆的蠕变性能,造成预应力损失[7]。因此,对于锚杆蠕变性能的研究显得很有必要。选取编号为1#、2#、3#、4#的CFRP/GFRP锚杆进行分析,具体数据见表2。

表2 CFRP/GFRP锚杆分组

注：极限荷载=σgAg+σcAc+σmAm

近半个多世纪以来,有关研究人员在通过对大量不同性质的材料进行蠕变试验的基础上,总结出了蠕变理论及各种不同性质材料的蠕变粘弹性性质,并提出了不同适用条件下的蠕变本构模型。BURGERS模型被作为GFRP抗浮锚杆的蠕变本构模型[8],BURGERS模型是一个四元件模型,对复杂的粘弹性材料的蠕变性能有很好的表征。其组成方式见图2。

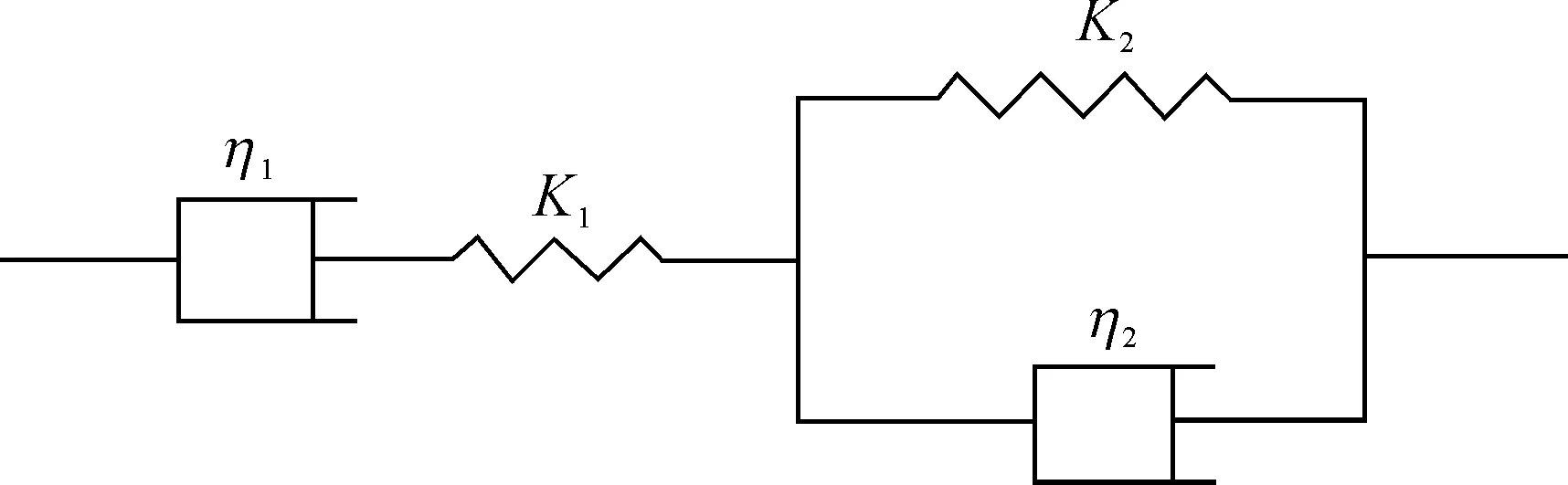
图2 BURGERS模型[9]

Burgers模型的其蠕变方程可表达为：

(7)

式中:u为蠕变位移；F为所施加的荷载；K1为次蠕变模量；K2为主蠕变模量；η1为次蠕变阻尼；η2为主蠕变阻尼。

因本文对锚杆的蠕变性能为纯理论分析,缺少实验数据,无法得到相关参数的值。因此,蠕变模型中CFRP/GFRP1#锚杆各力学参数取值参考文献[8]中的参数数据。文献[8]中的参数通过联立回归分析方程和蠕变本构方程得到,而回归分析方程是通过蠕变试验所得的试验数据得到[10]。蠕变本构模型各力学参数K1、K2、η1、η2主要受碳纤维含量影响,随碳纤维含量的增加,参数取值增大。K1取值范围为60～140 kN·mm-1,K2取值范围为40～100 kN·mm-1,η1取值范围为-1 000～-1 800 kN·d·mm-1,η2取值范围为550～1 100 kN·d·mm-1。考虑同一根锚杆在不同加荷等级下产生变形损伤,因此同一模型在不同受力状态下参数取值不同。

将各力学参数代入蠕变方程,得到4组CFRP/GFRP锚杆时间-位移曲线,见图3～6。其中150 kN荷载作用下不同碳纤维含量CFRP/GFRP锚杆时间-位移曲线见图7。产生蠕变的荷载与碳纤维含量关系见图8。

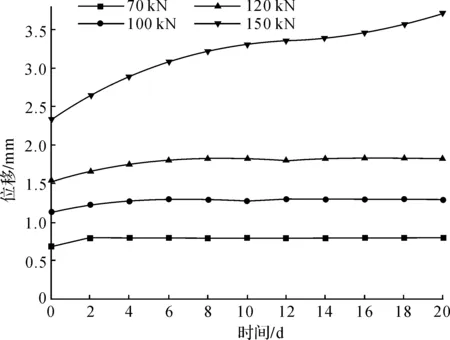
图3 CFRP/GFRP 1#锚杆时间位移曲线

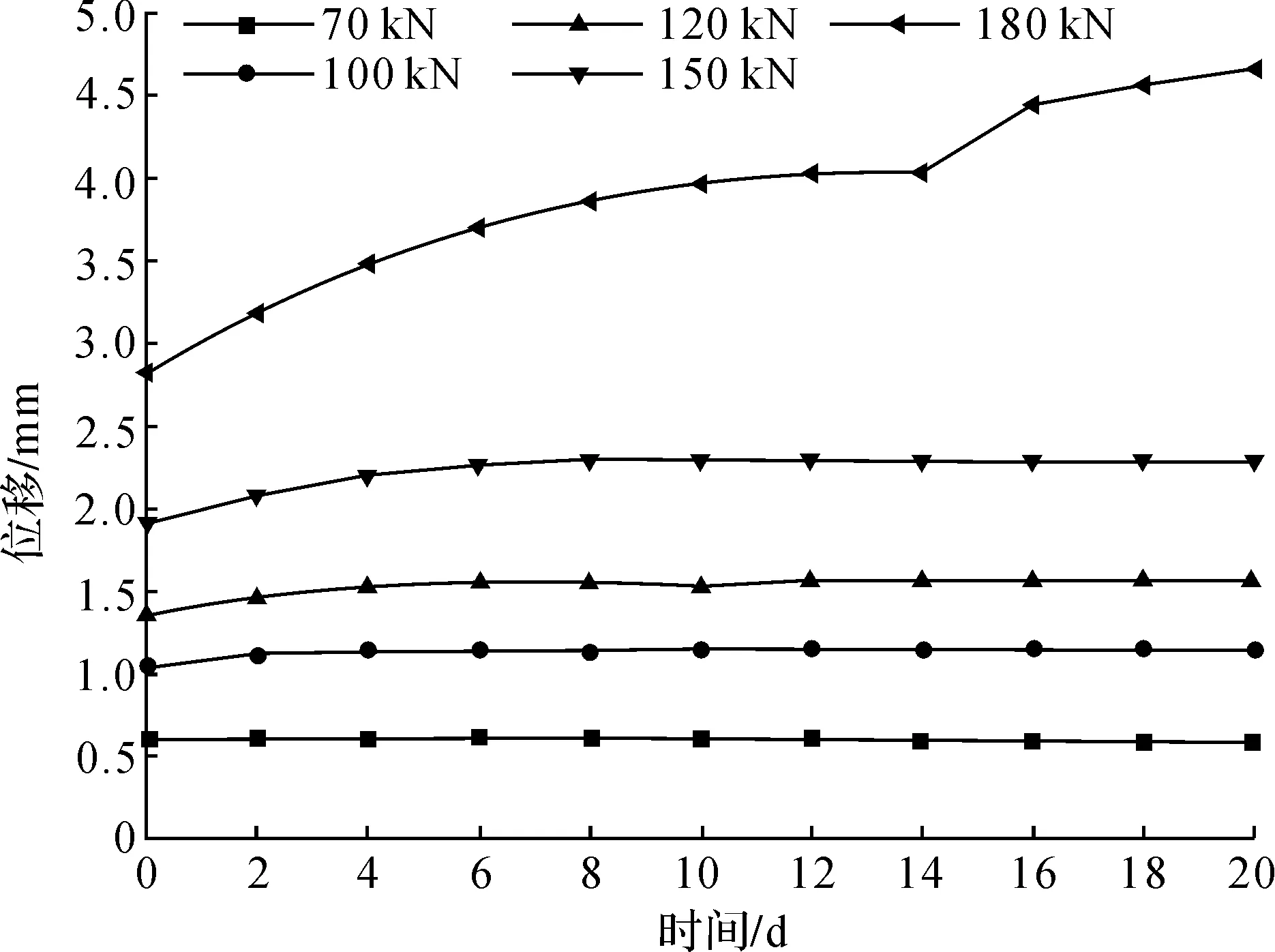
图4 CFRP/GFRP 2#锚杆时间位移曲线

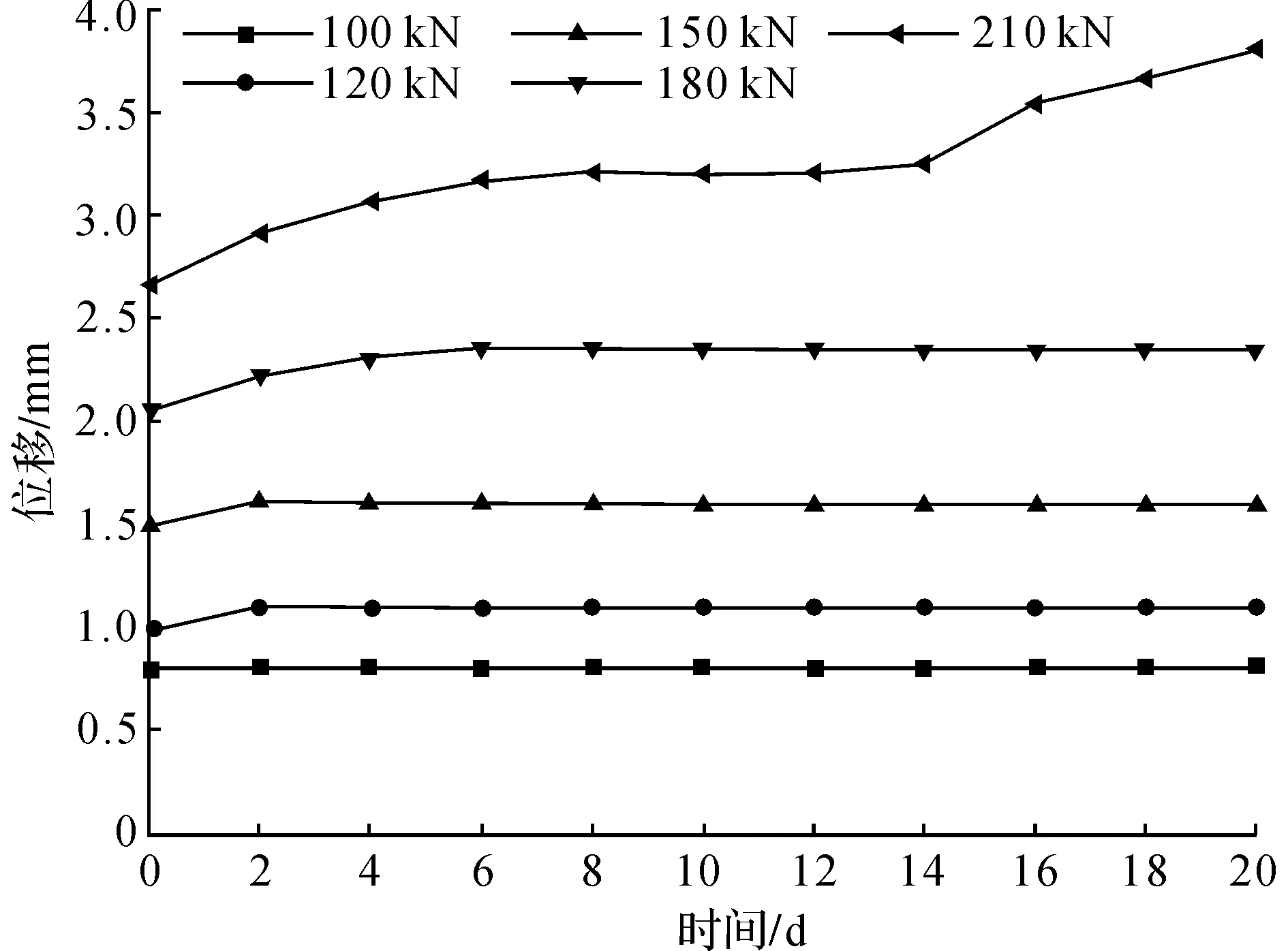
图5 CFRP/GFRP 3#锚杆时间位移曲线

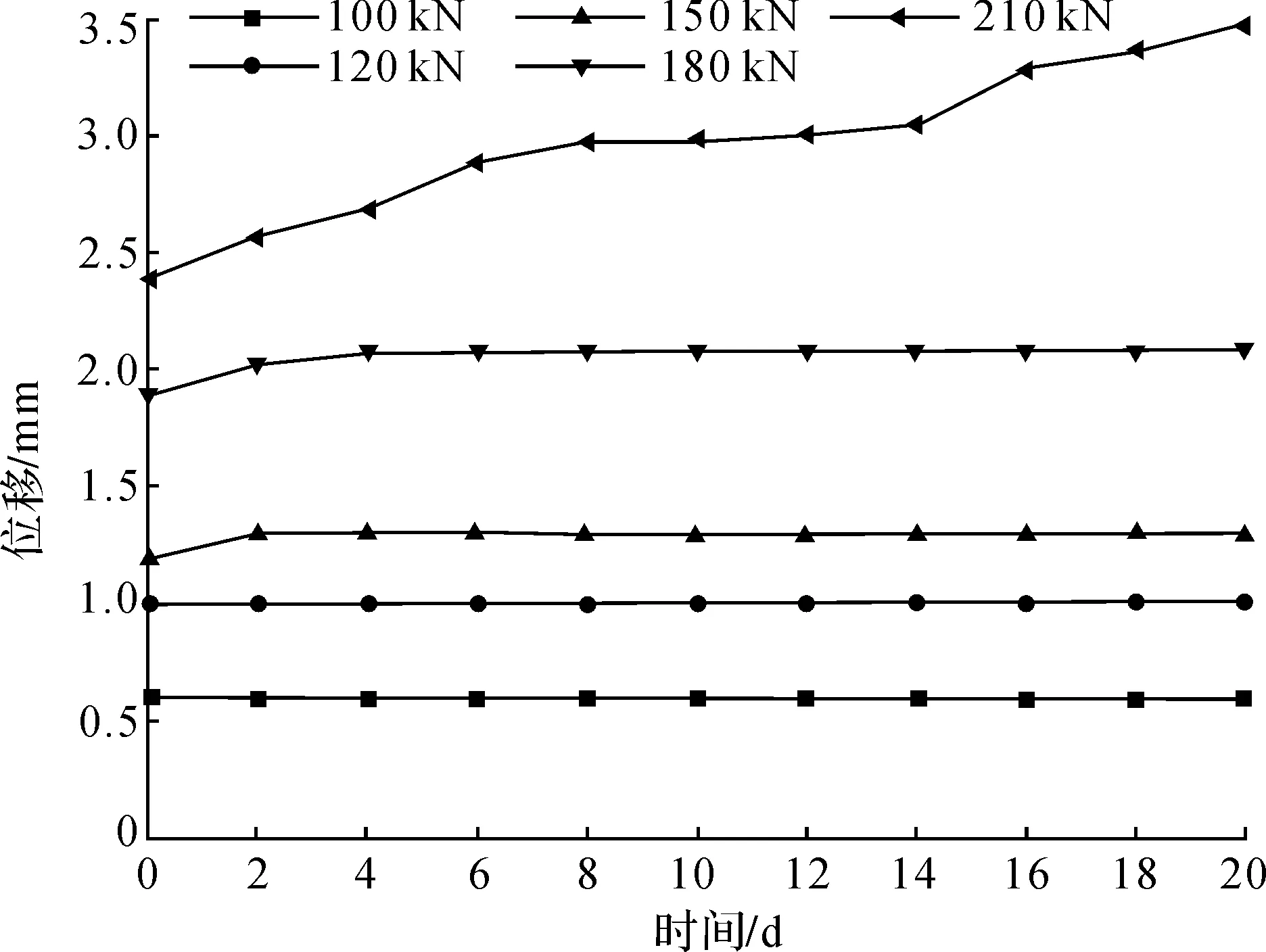
图6 CFRP/GFRP 4#锚杆时间位移曲线

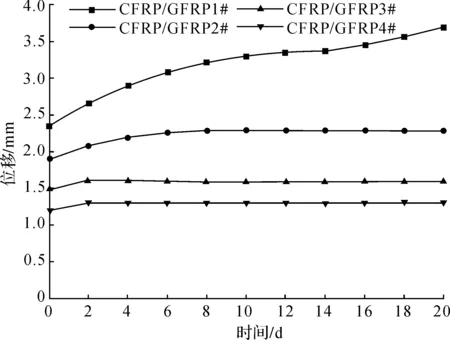
图7 150 kN荷载下不同碳纤维含量锚杆时间位移曲线

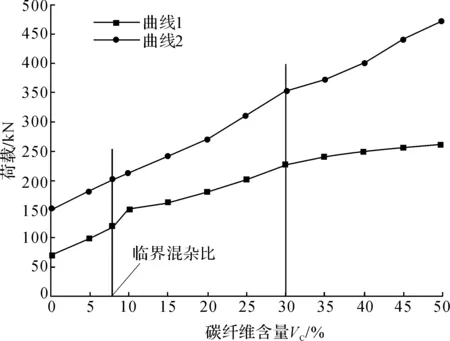
注：曲线1为产生起始蠕变的荷载曲线；曲线2为产生不稳定蠕变的荷载曲线。图8 产生蠕变的荷载与碳纤维含量关系

由图3～6可看出,随着碳纤维含量的增加,1#、2#、3#、4#中锚杆发生蠕变现象的应力水平为70、100、120、150 kN,分别为极限荷载的40%、50%、55%、60%。即GFRP锚杆在40%的极限荷载下就会发生蠕变现象,而CFRP/GFRP混杂锚杆需要至少50%以上的极限荷载时才会发生蠕变现象。

从图7中可看出,在施加同一级荷载水平下,随着碳纤维含量的增加,CFRP/GFRP锚杆蠕变位移逐渐变小且混杂碳纤维的CFRP/GFRP锚杆的蠕变位移比单一GFRP锚杆的蠕变位移减少了40%以上。由此可见,碳纤维复合材料能有效改善GFRP锚杆的蠕变性能。

由图8可知,曲线1以下的荷载范围内不会产生蠕变现象,在曲线1和曲线2之间荷载范围内产生稳定蠕变,超过曲线2的荷载范围则产生不稳定蠕变。因此,在工程中应将锚杆的工作荷载控制在曲线2以下范围内,这一结论也可为CFRP/GFRP锚杆蠕变试验时施加荷载提供参考。由曲线1可知,在临界混杂比之前,碳纤维含量对蠕变性能的影响较为明显,随着碳纤维含量的增加,发生蠕变所需要的荷载变大,说明在此阶段碳纤维含量对蠕变性能影响较大；而在临界混杂比之后,随着碳纤维含量增加,发生蠕变的荷载变化减小且逐渐趋于稳定,说明在此阶段碳纤维含量对蠕变性能影响逐渐减小。由此可知,过多地加入碳纤维只起到增大强度的作用而对蠕变性能影响并不大;因此,在考虑碳纤维利用率以及工程实际成本上,最好控制混杂纤维锚杆碳纤维含量在30%以内。

3 结 语

理论研究表明,CFRP/GFRP混杂纤维锚杆表现出良好的强度以及蠕变性能,能显著改善单一GFRP锚杆易脆断、耐久性差等缺点。根据两种不同锚杆拉伸强度计算方法、不同碳纤维含量对锚杆蠕变性能影响的理论分析,得出以下结论：碳纤维含量能显著提高GFRP锚杆的强度, 且碳纤维含量与

拉伸强度总体呈线性关系。为了得到较高的拉伸强度,碳纤维含量应大于临界混杂比γ；在进行强度理论计算时应考虑基体的影响,修正后的式(5)和式(6)可以作为拉伸强度理论计算公式；碳纤维复合材料能有效改善GFRP锚杆的蠕变性能,可将起始蠕变的应力状态提高,从而提高锚杆材料的强度利用率,同时可减小锚杆的蠕变量值,进而减轻锚杆使用过程的预应力损失。由蠕变的荷载与碳纤维含量关系曲线图,可以得到锚杆工作荷载及蠕变试验的荷载控制范围,有利于实际现场控制锚杆应力及锚杆蠕变试验荷载设计；综合考虑CFRP/GFRP锚杆的强度性能与蠕变性能,碳纤维含量应控制在8%～30%之间比较合适。

[1] ZENG Q D, FAN F Q.A random critical-core theory of micro-damage in interplay hybrid composites :I—first failure and hybrid effect [J]. Composites Science and Technology, 1993,49(3):341-348. [2] 张自荣,朱坤,石桂梅. 碳纤维/玻璃纤维加固钢筋混凝土结构新技术[J]. 长春工程学院学报:自然科学版,2001,2(2)：18-20．

[3] 邓宗才,李建辉.混杂FRP复合材料混杂效应的研究与进展[J]. 玻璃钢/复合材料,2008(1)：9-13．

[4] 何小兵,曹勇,严波,等. GFRP/CFRP层间混杂纤维复合材料极限拉伸性能[J]. 重庆交通大学学报：自然科学版,2013,32(6):1153-1156．

[5] 曾新芳. 新型玻璃钢锚杆的试验研究[D]. 北京：北京化工大学,2011．

[6] 陈汝川. 混杂纤维复合材料受拉构件的最优混杂比研究[J]. 固体火箭技术,2005,28(3):219-221．

[7] 夏建中,潘晓东,钱波. CFRP嵌入式加固钢筋混凝土结构研究及在基坑工程中的应用探索[D]. 杭州：浙江工业大学,2013．

[8] 张舜泉. 长期荷载作用下GFRP抗浮锚杆蠕变性能研究[D]. 青岛：青岛理工大学,2014．

[9] 蒙上阳,唐国金. Burgers模型的参数获取方法[J]. 固体火箭技术,2003,26(2)：27-29．

[10] 许宏发. 多项式回归间接求解岩石流变力学参数的方法[J]. 有色金属,1994,46(4)：19-22．

Discussion on the Action Mechanism and Design Theory of the CFRP/GFRP Hybrid Fiber Anchor

ZHULanyan1,ZHANGXuefeng2

2016-06-27

浙江省科技厅公益技术研究社会发展项目(2015C33019)

朱蓝燕(1992—)，女，浙江衢州人，硕士在读。

TU313

A

1008-3707(2016)11-0024-05