低抖动时钟产生电路设计

江 平，叶宝盛

(中国电子科技集团公司电子第36研究所，嘉兴 314033)



低抖动时钟产生电路设计

江 平，叶宝盛

(中国电子科技集团公司电子第36研究所，嘉兴 314033)

相位噪声和抖动是考量周期信号性能最常用的2个指标。介绍了相位噪声和抖动的概念，详细分析了两者之间的联系，设计了一个低抖动的标频时钟模块，测试结果表明均方根(RMS)周期抖动≤250fs。

时钟模块；相位噪声；抖动

0 引 言

时钟信号是电子系统中必不可少的，其稳定度是影响系统性能的关键指标。随着技术的发展、工作速度的提高，系统对时钟稳定度也提出了更高的要求[1]。本文设计了一个低抖动的标频时钟模块，通过理论计算和实测得到其均方根(RMS)抖动，很好地满足了系统的应用要求。

1 基本概念及理论分析

1.1 相位噪声

理想的振荡器输出为一正弦波，只存在单一频率，其频谱为单一脉冲[2]，如图1所示。而实际的振荡器输出不是理想的正弦波，其幅度和相位都是随时间变化的，可以表示为：

Vo(t)=A(t)cos[ω0t+φ(t)]

(1)

由于A(t)和φ(t)的影响，实际振荡器输出波形的频谱在中心频率两侧存在边带，如图2所示。

图1 理想振荡器输出频谱

图2 实际振荡器输出频谱

相位噪声定义为在某一频偏处，1Hz带宽内单边带噪声谱密度与载波功率的比值，通常对该值取对数，单位dBc/Hz，见公式(2):

(2)

式中：Psideband(ω0+Δω,1Hz)为单边带频谱上与载波频率ω0偏移Δω处1Hz带宽内的噪声功率[3]。

1.2 抖动

相位噪声从频域上描述了信号稳定度，而抖动则从时域上表征了信号的稳定度，反映了周期信号偏离理想位置的程度。按照不同的类型，抖动可以分为周期间抖动、周期抖动和长周期抖动，其中周期抖动较为常用。

周期抖动(Jper)是信号实测周期与理想周期之间的时间差。假设时钟信号的理想周期为T0，第i个周期为Tper(i)，则第i个周期抖动表示为：

Jper(i)=T0-Tper(i)

(3)

(4)

1.3 相位噪声与时钟抖动的关系

相位噪声和时钟抖动是对时钟性能在频域和时域上的描述，本质上是相同的，因此两者之间必然存在内在的联系[1]。

在应用中由于限幅器等作用，幅度随时间的变化通常可以忽略不计，即式(1)可以表示为：

(5)

则第i个周期抖动可以表示为：

(6)

式中：Δφi为第i个周期的相位误差。

(7)

(8)

所以：

(9)

而其中LΔφ(fm)与相位噪声L(fm)存在如下关系：

L(fm)=10lgLΔφ(fm)

(10)

将式(10)代入式(9)，可得：

(11)

式(11)表明了周期抖动和相位噪声两者之间的相互转换关系，通过该式可以在测试出相位噪声的情况下近似计算周期抖动。

2 标频时钟模块设计与测试

2.1 标频时钟模块电路设计

本文设计了一个低抖动的标频时钟模块，提供时钟信号10MHz、92.16MHz、204.8MHz各1路及100MHz2路。模块内部包含二分路单元、三分路单元、102.4MHz锁相分路单元、92.16MHz锁相单元和204.8MHz锁相单元等主要电路，组成框图见图3。

图3 标频时钟模块组成框图

二分路电路将10MHz铷钟信号功分成2路，一路给锁相晶振提供参考时钟，另一路则对外输出。在二分路电路的2个输出支路上加衰减和放大电路，以增大两输出电路之间的隔离。

三分路电路将锁相晶振的输出分成3路，2路放大、滤波后对外提供2路100MHz信号，第3路则作为102.4MHz锁相分路电路的参考时钟。

102.4MHz锁相分路电路用于产生92.16MHz锁相电路和204.8MHz锁相电路所需的参考时钟。本电路采用HMC830锁相环芯片，100MHz参考，4MHz鉴相，整数分频，锁相环产生2 048MHz的频率信号，经芯片内部后级分频器20分频，实现102.4MHz信号的锁相输出，经二分路电路分路、放大、滤波后作为92.16MHz和204.8MHz锁相电路的参考。

92.16MHz锁相电路采用HMC830单环，102.4MHz参考鉴相，整数分频，实现92.16MHz信号的锁相，放大、滤波后对外输出。204.8MHz锁相电路同样采用上述结构，硬件电路可基本移用，只需向HMC830芯片的内部寄存器写入所需频率对应的值即可。

2.2 相位噪声和周期抖动的理论计算

本设计采用的100MHz锁相晶振的相位噪声见表1。其中未能从手册中找到的数据通过理论及常规情况估计。

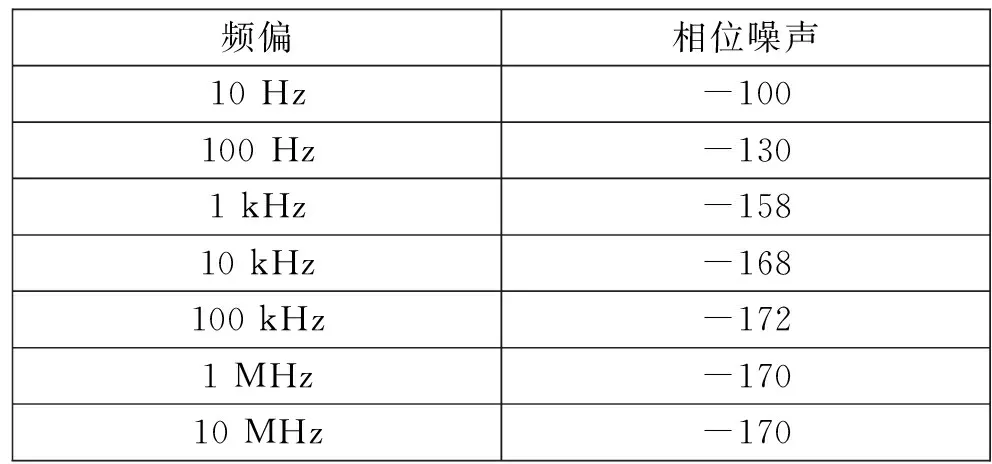
表1 锁相晶振相位噪声

102.4MHz参考时钟采用HMC830芯片搭建锁相环单环实现，环路带宽约200kHz，下面估算其相位噪声。

整数分频工作模式下，HMC830的基底噪声为-230dBc/Hz，可估算其对102.4MHz的带内噪声为：-230+10lg(4 000 000)+20lg(2 048/4)-20lg20≈-135.8dBc/Hz，而带外则由内部压控振荡器(VCO)确定。可得其相位噪声，见表2。

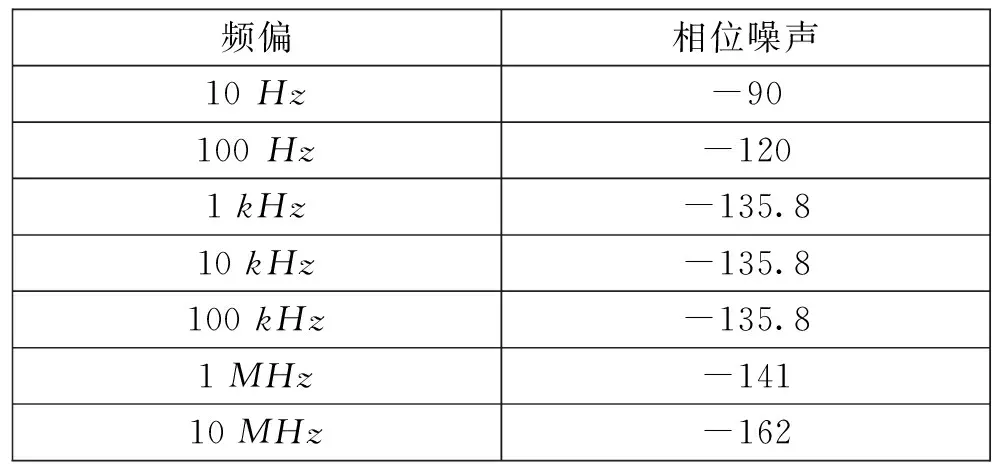
表2 102.4MHz参考信号相位噪声

同理，可以计算得到204.8MHz信号的相位噪声，见表3。

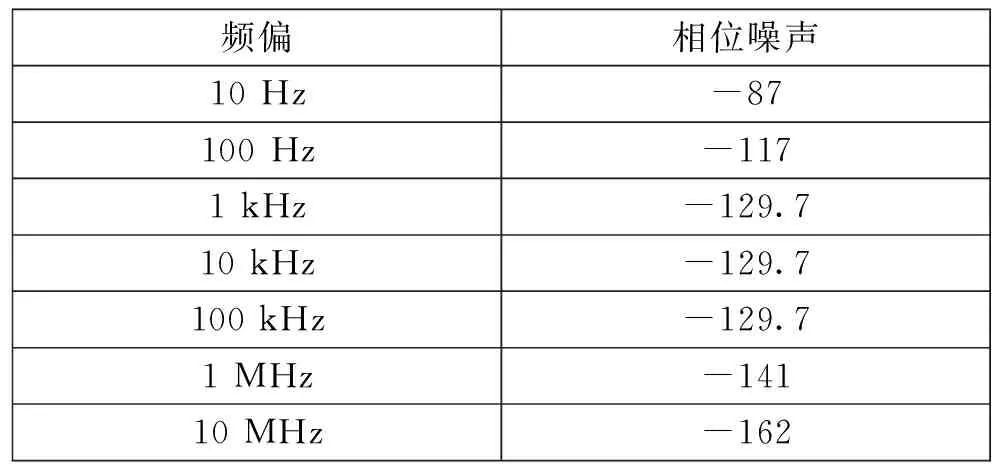
表3 204.8MHz参考信号相位噪声

通常在工程上可以用分段函数来描述相位噪声和频偏之间的关系，则表3中204.8MHz信号的相位噪声如图4所示。那么，L(f)在数学上可以表示为：

(12)

(13)

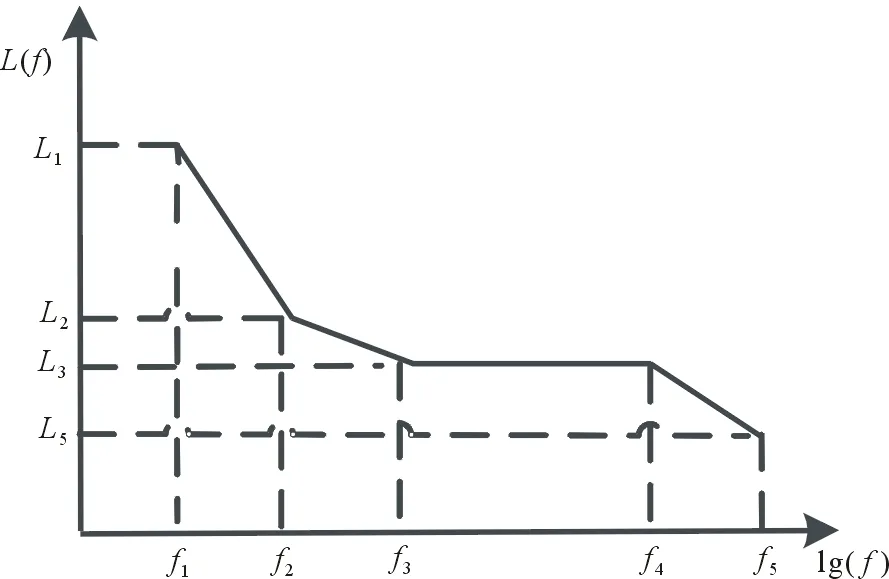
图4 估算的204.8 MHz信号相位噪声曲线

将公式(12)、(13)代入公式(11)，可得:

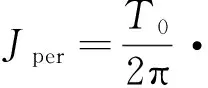
(14)

通过Matlab编程计算，可得204.8MHz时钟信号在频偏10Hz～10MHz范围内的RMS周期抖动为225.6fs。

2.3 相位噪声和周期抖动的测试

理论分析和计算得出了周期抖动的值，以下给出实物测量的结果。标频时钟模块实物见图5。

图5 标频时钟模块实物

首先给该模块加电，用相位噪声分析仪E5052测试204.8MHz端口的相位噪声及RMS抖动，记录测试曲线,如图6所示。由图6可得，频偏10Hz、100Hz、1kHz、10kHz、100kHz、1MHz和10MHz处的相位噪声分别是-83、-120、-128、-133、-131、-146、-169。频偏10Hz～10MHz内RMS周期抖动值为237fs。

图6 实测204.8 MHz信号相位噪声曲线

2.4 计算与实测结果比较

通过比较发现，理论计算的周期抖动值与实测值基本吻合，只存在5%的误差，因此该估算模型能够很好地指导电路设计。而误差主要由以下两方面原因造成：

(1) 相位噪声预估误差。相位噪声的估算不准确，和实测的相位噪声值存在一定的差异。

(2) 相位噪声曲线的分段线性近似。实测相位噪声曲线并不是理想的分段线性函数，而计算中则采用了分段线性函数近似。

3 结束语

本文阐述了相位噪声和时钟抖动这2个基本概念及两者之间的关系，设计了一个低抖动的标频时钟模块，给单机和系统提供10MHz、100MHz、92.16MHz和204.8MHz这几路时钟信号，通过计算和实测结果的比较，验证了相位噪声和抖动之间的关系。测试结果表明该设计能够实现低抖动的时钟信号输出，满足系统应用要求。

[1]ZANCHIA，BONFANTIA，LEVANTINOS，etal．Cycle-to-cyclejitterrelationshipwithapplicationtothephasenoiseinPLL[C]//SouthwestSymposiumonMixed-signalDesign.Austin，Texas,America，2001：32- 37.

[2]RAZAVIB.模拟CMOS集成电路设计[M].陈贵灿译.西安：西安交通大学出版社,2003.

[3]HAJIMIRIA,LEETH.Ageneraltheoryofphasenoiseinelectricaloscillators[J].JournalofSolid-stateCircuits,1998,33(2):179-194.

DesignofLow-jitterClockGenerationCircuit

JIANGPing，YEBao-sheng

(No.36ResearchInstituteofCETC,Jiaxing314033，China)

Phasenoiseandjitteraretwoindexestoevaluatetheperformanceofperiodicsignal.Thispaperintroducestheconceptionsofphasenoiseandjitter,analyzestherelationbetweenthemindetail,designsaclockmodulewithstandardlow-jitterfrequency.Thetestresultindicatesthattherootmeansquare(RMS)periodicjitterisn'tmorethan250fs.

clockmodule;phasenoise;jitter

2015-08-12

TN

A

CN32-1413(2016)05-0117-04

10.16426/j.cnki.jcdzdk.2016.05.029