基于广义模糊函数的低分辨雷达目标识别

陈 辉，丁 宇，焦小辉，徐小川

(解放军95980部队，襄阳 441500)



基于广义模糊函数的低分辨雷达目标识别

陈 辉，丁 宇，焦小辉，徐小川

(解放军95980部队，襄阳 441500)

针对低分辨雷达的特点，提出了广义模糊函数的概念，讨论了广义模糊函数与目标分辨率的关系，通过分析广义模糊函数中3个参数的构成，对编队目标架次识别方法进行了研究，并通过实例进行检验，为实际工程运用提供了参考。

低分辨雷达；广义模糊函数；目标识别

0 引 言

对于低分辨率雷达而言，空中目标为点目标，要求对其进行精细识别是不切实际的[1-3]。低分辨雷达的特点是脉宽较大、频带较窄。脉宽大导致目标径向距离上的分辨率差，基于A显目标回波波形特征的目标识别方法[4]等就是在致力于解决此背景下的目标识别问题；频带窄导致目标多普勒频率上的分辨率差，基于连续小波变换(CWT)的目标识别方法[5]等就是致力于解决此背景下的目标识别问题。

通过研究模糊函数发现，模糊函数集成了目标回波的时域和频域特征，它不但描述了雷达信号时延-频移联合估计最佳处理器输出的全影图像，而且给相邻目标距离-速度联合分辨提供了一个保守的估计[6]。本文提出广义模糊函数的概念，并运用广义模糊函数对编队目标架次识别方法进行分析。

1 模糊函数的定义

定义二维模糊函数A(Td,Fd)∈[0,1]，它是与时间及频率均有关的复合自相关函数：当|A(Td，Fd)|2/A2(0,0)=1时，表示目标无法分辨；当|A(Td，Fd)|2/A2(0,0)略小于1时，表示目标很难分辨；当|A(Td，Fd)|2/A2(0,0)≪1时，表示目标很容易分辨。

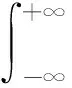
(1)

或写成频率表达式为：

(2)

对于式(2)，当Fd=0时，便得到一维距离模糊函数；Td=0时，得到一维速度模糊函数。

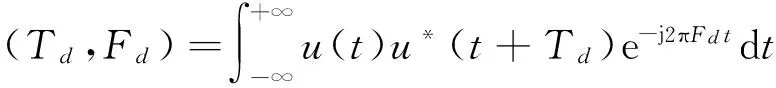
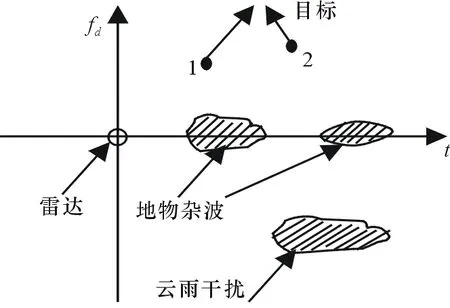
图1 目标环境图

现以目标1为基准，即以目标1为(τ，fd)平面的坐标原点画出信号模糊度图(如图2所示)。“椭圆”区域内为模糊区，如目标2′处于模糊区，此时无法区分目标1与目标2′；“椭圆”区域外为非模糊区，如目标2处于非模糊区，此时能够区分目标1与目标2。因此，模糊函数给相邻目标距离-速度联合分辨提供了一个保守的估计。

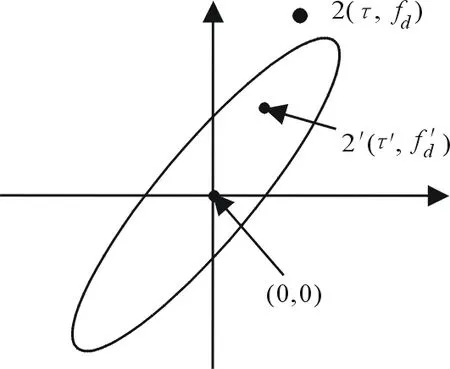
图2 雷达信号模糊度图

2 广义模糊函数及其分辨率的概念

由模糊图概念可知，当|A(Td，Fd)|2/A2(0,0)=1时，表示目标无法分辨；但当两目标时延差Td和多普勒频率差Fd都相同时，而方位上存在差异，认为目标仍可分辨。为此引入方位角β和俯仰角ε来表示目标的位置。

如图3所示，两目标分别以速度v1和v2编队飞行，目标1、2距雷达分别为R1和R2，方位角分别为β1和β2，仰角分别为ε1和ε2。当R1=R2，且v1和v2速率相同时，两目标径向雷达方向飞行，此时虽然Td=0、Fd=0目标在时频域上无法分辨，但目标在仰角上的差异和方位上的差异为目标架次识别提供了可能。

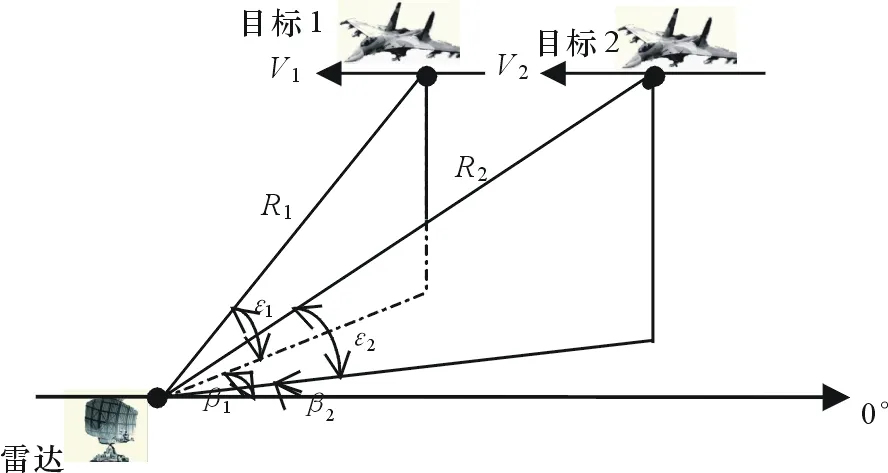
图3 窄带雷达2个探测目标模型

设发射信号包络为u(t)，考虑到目标方位与仰角的作用，定义广义模糊函数为：

(3)

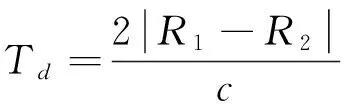
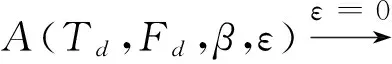
(4)

从物理意义上讲，增加方位角β(β≥0)参量，相当于模糊函数值降低eβ(eβ≥1)倍，这就给目标识别带来得益。

3 广义模糊函数对目标识别的启示

对广义模糊函数A(Td,Fd,β)任意提取3个参数中的2个参数，可得到广义模糊函数的二维切片，即A(Td,Fd)、A(Td,β)和A(Fd,β)，其中A(Td,Fd)是本文第一部分所述的经典模糊函数，而切片A(Td,β)和A(Fd,β)定义为时间-方位模糊函数和频率-方位模糊函数；若提取模糊函数中的每个参数，则可得到它的一维切片，即时间维A(Td)、频率维A(Fd)和方位维A(β)。不难发现，不论是对广义模糊函数本身，还是对其二维切片A(Td,β)和A(Fd,β)和一维切片A(β)，方位因素影响能够独立开来，呈指数下降趋势，即方位角每增大Δβ，相当于模糊函数值降低eΔβ倍。因此，提高方位测量精度，在目标识别上所获得的得益要比在时域和频域上大得多。

雷达PPI显示器上目标图像之所以被展宽是因为目标分布与天线方向图卷积的结果。显示器上目标沿方位上的展宽角度与波束宽度相同。如果两目标角度间隔小于波束宽度，则2个靠近的点目标不能分辨。但在目标探测过程中雷达天线是旋转的，这就为方位角分辨率的改善提供了潜在的可能。其基本思想是：把目标看成1个序列，接收信号是目标序列合天线方向性函数的卷积，采用某种运算把接收序列中天线方向性函数去掉，只剩下目标序列，这样雷达便得到更佳的分辨率，具体方法如下。

图4 去卷积方法原理图

那么，接收机输出视频信号为：

y(n)=x(n)⊗g(n)+N(n)

(5)

根据噪声是否可以忽略可分2种情况：

(1) 假设N(n)=0，则式(5)变为:

y(n)=x(n)⊗g(n)

(6)

在频域上为：

Y(K)=X(K)G(K)

(7)

设计去卷积滤波器，令：

H(K)=1/G(K)

(8)

则：

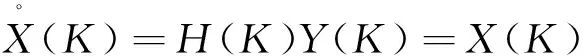
(9)

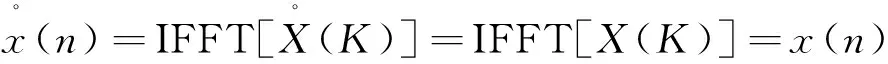
(10)

从上式看出可从y(n)中完全恢复目标x(n)。

(2) 假设N(n)≠0，即不能忽略噪声影响，则式(5)在频域的表达式为:

Y(K)=X(K)G(K)+N(K)

(11)

在维纳准则下，设计最佳去卷积滤波器的滤波方程为：

H(K)=G*(K)/[|G(K)|2+Pn(K)/Px(K)]

(12)

式中：G*(K)为G(K)的复共轭；Pn(K)为噪声N(t)的功率谱密度；Px(K)为x(t)的功率谱密度。

由于Pn(K)和Px(K)是未知的，可以假定Pn(K)/Px(K)等于常数。

雷达P显回波的特点在于它包含了回波方位信息，雷达波瓣较宽导致常规情报雷达方位分辨性能不高，对编队飞机目标，尤其是密集编队情况，其架次识别能力较差。但是波束随天线的转动扫描为识别性能改善提供了可能。以上分析表明，使用周期脉冲、运用信号处理方法，对目标架次识别能够实现较大的得益。所以，在肯定基于P显目标回波图像特征的识别方法有效性的同时，建议先从使用周期脉冲、提高方位分辨率入手，进行架次识别。

4 举例说明

假设雷达天线以6转/min的速度旋转，脉冲重复频率为300 Hz，天线转360°共需要10 s，每转共发射脉冲10×300=3 000个，在PPI显示器上，每个回波脉冲对应的分辨率为360°/3 000=0.12°，而雷达天线水平波瓣宽度通常大于1°(约1.1°)，这样，方位分辨率在理论上提高了近10倍。显然对目标架次的识别使用脉冲识别比使用方向图识别会有较大的得益。

5 结束语

本文研究了模糊函数、广义模糊函数及其与目标分辨率之间的关系。通过分析广义模糊函数中3个参数的构成，认为方位角分辨率的改善会对目标识别效果产生更大的增益，因此跳出天线方向图对方位分辨率的影响，从脉冲积累考虑，采用去卷积的方法，能够还原目标序列，并从实例证明该方法在理论上具有可行性，但其具体的工程实现问题有待于进一步研究。

[1] 王利华．基于低分辨雷达的目标识别方法研究[D]．南京：南京理工大学出版社，2008．

[2] 赵晓平．低分辨雷达目标识别研究[D]．大连：大连理工大学，2010．

[3] 米红妹．低分辨雷达目标识别的应用研究[D]．大连：大连理工大学，2011．

[4] 张汉华，王伟，姜卫东，等．低分辨雷达基于波形特征的飞机架次判别方法[J]．国防科技大学学报，2003(4)：38-52．

[5] 李侠．现代雷达技术[M].北京：兵器工业出版社，2000．

[6] 时银水，姬红兵，王磊．基于CWT的常规雷达目标架次自动识别[J]．现代雷达，2007，29(7)：34-37．

Target Recognition for Low Resolution Radar Based on Generalized Fuzzy Function

CHEN Hui，DING Yu，JIAO Xiao-hui，XU Xiao-chuan

(Unit 95980 of PLA,Xiangyang 441500，China)

Based on the characteristics of low resolution radars,this paper puts forward the concept of generalized fuzzy function,discusses the relationship between the generalized fuzzy function and target resolution,studies the recognition method of formation target sortie by analyzing the composing of three parameters in generalized fuzzy function,and checks the method through practical example,which presents reference for practical engineering application.

low-resolution radar；generalized fuzzy function；target recognition

2016-01-19

TN957.51

A

CN32-1413(2016)05-0046-04

10.16426/j.cnki.jcdzdk.2016.05.011