基于改进变步长自适应滤波的密集假目标干扰抑制方法

周文辉，闵柏成

(1.解放军91404部队，秦皇岛 066001；2.中国船舶重工集团公司第723研究所，扬州 225001)



基于改进变步长自适应滤波的密集假目标干扰抑制方法

周文辉1，闵柏成2

(1.解放军91404部队，秦皇岛 066001；2.中国船舶重工集团公司第723研究所，扬州 225001)

提出了一种基于改进变步长自适应滤波的密集假目标干扰抑制方法。该方法首先采用stretch去斜处理，消去信号的二次项，并在频域上分离目标回波与干扰，从而得到频率不同的信号分量;然后用基于类箕舌线函数的变步长自适应滤波方法，对stretch处理后的回波信号滤波;最后对消密集假目标干扰，将对消后的信号作逆stretch处理恢复目标回波。所提出的类箕舌线函数调节自适应滤波方法中的步长，能有效地抑制距离目标回波较近的假目标干扰。仿真结果表明，改进变步长自适应滤波方法在目标回波与干扰时延差较小时，也可有效地对回波信号滤波，干扰对消效果明显；与基于定步长的滤波方法相比，所提方法在信干比较低的环境下仍具有良好的鲁棒性，并能有效抑制密集假目标干扰。

密集假目标；stretch处理；变步长；自适应滤波；干扰抑制

0 引 言

近年来，数字技术的进步及高性能处理芯片的发展，为数字射频存储器(DRFM)技术打下了良好的基础，形成了DRFM干扰技术[1]。密集假目标干扰基于数字射频存储器，其通过对接收到的雷达回波信号进行高速采样，保存回波信号的实时样本，经多次延迟、叠加和调制，产生大量的假目标干扰[2]，在数量上达到对雷达欺骗的目的，使雷达不能检测出真实目标或者不能正确测量真实目标的参数信息。密集假目标干扰可在频域上与目标的回波重叠，由于线性调频(LFM)雷达通常具有较大的时宽，因而假目标干扰在时域上通常也与目标回波高度耦合[3]。另外，干扰方对目标实施干扰时，目标回波与干扰间的空间角度、相对速度等因素影响都能导致干扰与目标回波的参数发生改变，进而使得干扰的参数随着这些因素的影响而呈现一种动态的变化过程[4]。基于DRFM技术的密集假目标欺骗式干扰成为LFM雷达的主要干扰形式[5]，因而针对密集假目标干扰，进行干扰抑制方法的研究，对电子战理论的丰富和发展具有重要意义。

DRFM密集假目标干扰与LFM雷达接收端的目标回波在时域及频域上高度耦合，因此常规雷达抗干扰措施的性能难以达到最优。针对此问题，目前已有多种欺骗式干扰的抑制方法。文献[6]采用巴克码对雷达发射脉冲进行调制，在雷达接收端经相应的匹配滤波器输出，从而抑制DRFM假目标干扰。然而，若雷达的发射波形不能在脉间进行转换，该方法性能就会退化甚至失效。文献[7]提出基于脉冲分集的有源假目标对抗技术，通过构造特殊的发射信号集，使雷达发射信号和干扰在频域上实现正交化，再在雷达接收端经多路匹配滤波输出，组合或合并匹配滤波后的信号完成干扰对消。由于该方法需要设置多路匹配滤波器，对硬件设备要求较高导致实用性不强。文献[8]利用正交基对雷达发射波形进行调制，使雷达脉冲实现正交化，经匹配滤波输出可抑制假目标干扰。但是此类方法需要对雷达发射脉冲作特殊调制导致普适性不强。采用传统的时频变换方法[9]可在某时域或频域采样点处得到分离的信号分量，然而，当目标回波与干扰高度耦合，尤其是信号的相关参数总是动态变化时，处理后的目标回波与干扰在时频域上依旧存在高度耦合，难以提取目标信息。

针对DRFM密集假目标干扰与LFM雷达接收端的目标回波在时域及频域上高度耦合问题，本文首先采用stretch去斜处理[10]，在频域上分离目标回波与干扰，然后基于一种新的变步长自适应滤波方法对回波信号进行滤波，将滤波前后的信号对消后作逆stretch处理后即可恢复目标回波。利用该方法可有效地抑制密集假目标欺骗式干扰，无需估计干扰的相关参数，并能较好地恢复目标回波。

1 信号和干扰模型

LFM雷达为提高速度测量精度和速度分辨力，其发射信号通常具有较长的时宽与较大的带宽。因此，当干扰方对雷达实施密集假目标干扰时，目标回波与干扰在时域及频域上高度耦合。

设第l个脉冲重复周期雷达发射信号为：

(1)

sR(t,l)=a(l)sl′[t-τ(l)]

(2)

(3)

式中：a(l)为目标回波的幅度；τ(l)为目标回波的时延;fd(l)为目标回波的多普勒频移。

干扰方截获雷达发射信号的分量，并对截获的信号进行一定的幅度、延时等处理，使干扰与目标回波同时进入雷达接收机。其中，DRFM干扰机产生的假目标干扰模型如图1所示。

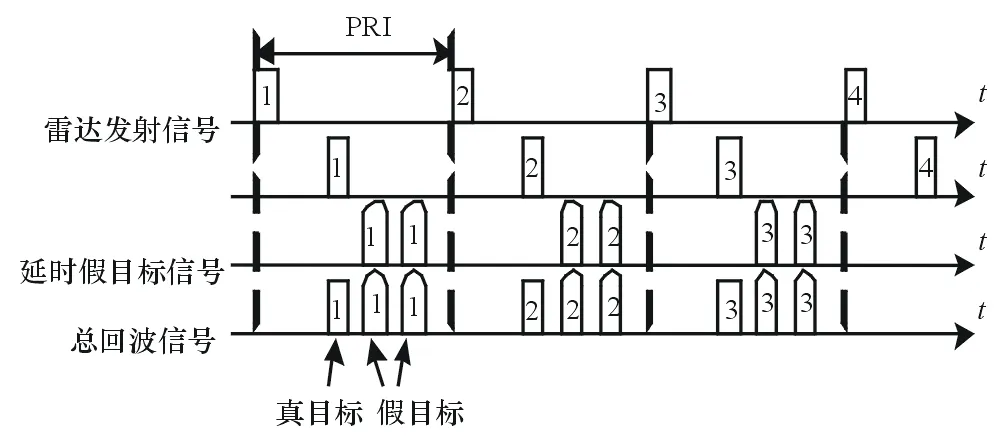
图1 DRFM延时转发假目标干扰模型

根据图1可以看出，若干扰方截获第l+1个脉冲重复周期的雷达发射信号分量，经一定的幅度、延时处理后转发到第l+1个脉冲重复周期，此时，雷达接收机接收到的信号同时包含目标回波与假目标干扰。一般情况下，上述接收信号中包含加性白噪声n(t)，且与n(t)独立。则在第l+1个脉冲重复周期中雷达接收信号的表达式为：

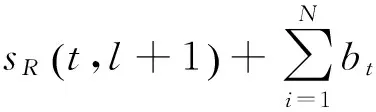
(4)

(5)

式中：bi(l+1)为第i个假目标干扰的幅度；σi(l+1)为第i个假目标干扰的时延;rdi(l+1)为第i个干扰的多普勒频移。

若干扰机将接收到的雷达信号作移频调制[11]，则可通过跨周期方式产生导前假目标干扰。假设干扰机截获了第l个脉冲重复周期的回波信号并作移频调制，则移频干扰的表达式为：

(6)

式中：λ(l)为移频干扰的幅度增益；fd为移频量；χd(l)为移频干扰的多普勒频移。

2 密集假目标干扰抑制算法

针对密集假目标干扰，首先要对干扰进行识别及检测，采用时频特性、统计信息及数字特征等[12]方法识别出假目标干扰，然后再对干扰进行处理。

2.1 stretch去斜及频域分离原理

设第l+1个周期中的雷达接收信号中含有目标回波和假目标干扰，同时包含加性白噪声。由于延时假目标干扰是通过截获雷达发射信号分量，经一定的幅度与时延等处理转发的，因而假目标干扰与加性白噪声独立。为便于推导且不失一般性，此处暂时忽略加性噪声的影响[13]。利用sR(t,l)对xl+1(t)作stretch处理，结合式(2)和式(4)可得：

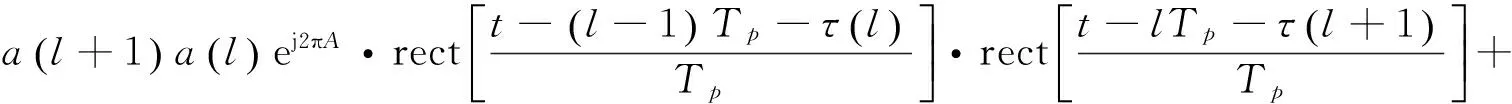
(7)

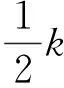
(8)

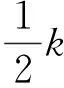
(9)

通过式(6)可得目标回波和延时假目标干扰相应的频率分别为：

ftarget=[fd(l)-fd(l+1)]+k[τ(l+1)-τ(l)]

(10)

fjam(i)=[fd(l)-rdi(l+1)]+ k[σi(l)-τ(l+1)]

(11)

式中：ftarget为stretch处理后目标回波的频率；fjam(i)为stretch处理后延时假目标干扰的频率,i=1,2,…,N。

根据式(6)～(8)可以看出，经stretch处理后的目标回波与假目标干扰均变为单频信号。考虑式(7)的第1项fd(l)-fd(l+1)=-2a/(cfp)，其中c为光速，a为目标加速度，fp为脉冲重复频率。实际中a≪cfp，所以式(7)第1项近似为零，从而ftarget主要由式(7)的第2项决定。当LFM雷达发射的脉冲频率很高时，目标回波在第l+1以及第l个脉冲周期间的时延差τ(l+1)-τ(l)极小，因此，经stretch处理后目标回波的频率ftarget位于接近于零的低频处。干扰方对雷达进行假目标干扰，为防止被雷达识别出来，必须限制干扰的加速度大小，因而式(8)中的fjam(i)主要由第2项决定。另一方面，为保证干扰方能有效干扰雷达目标，干扰方必须使干扰与目标间存在时延差，则有|σ2(l+1)-τ(l)|>|τ(l+1)-τ(l)|，故而经stretch处理后目标回波与假目标干扰的频率大小满足|fjam(i)|>|ftarget|。

如果干扰机对截获到的雷达信号作移频调制，将产生的导前假目标干扰作stretch处理，结合式(2)和式(4)可得：

(12)

式中：C=[fd(l)-χd(l)-fd]t+[fd(l)-χd(l)-fd]τ(l)。

由式(9)可以看出，经stretch处理后移频干扰也变为单频信号，其相应的频率为fyp=fd(l)-χd(l)-fd。通常情况下，干扰方产生移频干扰的移频量fd较大[14]，所以有|fyp|>|fjam(i)|>|ftarget|。

相邻周期间目标回波的时延差极小，而延迟假目标与目标回波间具有一定的时延差，匹配滤波后的延迟假目标滞后于目标回波。移频干扰是干扰机对截获到的雷达信号作移频调制产生的，干扰方可通过改变移频量的大小产生滞后或超前于目标回波的假目标干扰，且在通常情况下移频干扰的移频量较大。因此，采用stretch去斜处理可使LFM雷达回波与假目标干扰消去二次项，从而得到频率不同的信号分量，并在频域上分离目标回波与假目标干扰。

2.2 变步长自适应滤波器原理

频域分离处理后的干扰与目标回波对应的频率满足|fyp|>|fjam(i)|>|ftarget|，且ftarget位于接近于零的低频处。可充分利用这个信息，首先采用单频自适应陷波器[15]对频域分离处理后的回波信号陷波，然后对消密集假目标干扰，最终得到目标回波。单频自适应陷波器如图2所示。

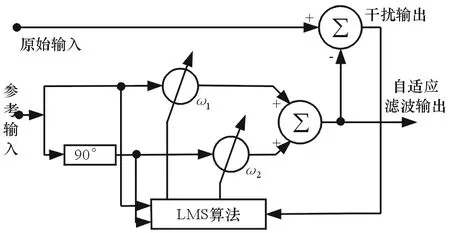
图2 单频自适应陷波器

图2中，原始输入为经stretch处理后的混合信号，混合信号包含经stretch处理后的目标回波和密集假目标干扰以及背景噪声，参考输入为频率为f0的正弦信号。

由原始输入到干扰输出的转移函数可表示为：

(13)

式中：f0为陷波频率；μ为步长；a为参考输入信号的幅度。

经stretch去斜处理后的干扰与目标回波对应的频率满足|fyp|>|fjam(i)|>|ftarget|，且ftarget位于接近于0的低频处，因此可令f0=0，代入式(13)得：

(14)

式(14)表明，此滤波器在单位圆z=1处存在一个零点，单位圆内距2μa2处存在一个极点。因此，滤波器可滤掉(0,ln(2μa2)/2π)范围内的频谱成分，其滤波带宽可通过改变μ的大小进行调整。

图2中自适应滤波算法采用一种新的变步长LMS算法，具体如下：

e(n)=d(n)-cT(n)ω(n)

(15)

(16)

ω(n+1)=ω(n)+2μ(n)e(n)c(n)

(17)

式中：e(n)为第n时刻的干扰输出；d(n)为第n时刻的期望输出信号；c(n)为第n时刻的参考输入矢量；ω(n)为第n时刻的权值；α控制函数的形状；β控制函数的取值范围。

式(15)为本文提出的一种类箕舌线函数的改进函数。图3为自适应滤波算法中定步长函数(Fixed)、sigmoid函数、箕舌线函数(Versiera)及本文所提出的类箕舌线函数(Proposed)对比图。其中横轴为干扰输出e(n)，纵轴为步长μ。

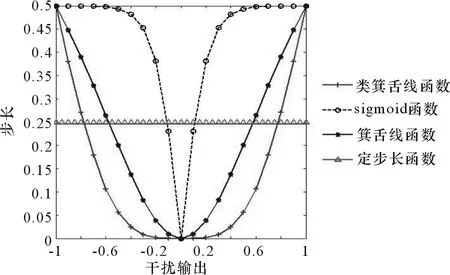
图3 常用步长函数曲线的对比

通过分析式(14)所示的转移函数可知，步长μ控制频域的陷波带宽。由图3可以看出，定步长函数的步长μ为固定常数，即无论干扰输出e(n)怎样变化，步长μ保持不变[16]。 因此,自适应算法在迭代过程中陷波带宽不变；基于sigmoid函数的改进曲线在稳态阶段e(n)的微小变化会引起步长μ较大的变化[17]；箕舌线函数曲线在e(n)的变化过程中步长μ始终在变化[18]，即迭代过程中陷波带宽始终是动态变化的。

步长μ值控制频域的陷波带宽，自适应算法在迭代的初始阶段，较大的步长可以有效地陷掉目标回波，同时消除目标回波由于频谱泄露产生的旁瓣部分。随着迭代次数的增加，过大的步长μ在陷波过程中会同时陷掉距离目标回波最近的干扰。当干扰与目标回波时延差较小时，导致对消后残留干扰的部分分量，使得恢复的回波信号中含有干扰分量。采用本文提出的基于改进函数的变步长自适应滤波方法，在迭代的初始阶段步长较大，从而陷波带宽较大；随着迭代次数的增加，μ随|e(n)|的减小而逐渐减小；达到稳态后μ几乎不变，从而保证了陷波带宽较小，可在目标回波与干扰时延差很小的情况下更好地对回波信号滤波。因此基于改进函数的变步长自适应方法能更有效地抑制密集假目标干扰。

2.3 密集假目标干扰抑制算法的步骤

(1) 通过式(7)、(12)对雷达接收机在第l个周期上的接收信号sR(t,l)与第l+1个周期接收信号xl+1(t)+syp(t,l)作stretch处理，其中l=1,2,…,M。

(2) 通过式(15)～(17)对stretch处理后的信号作滤波处理，并将滤波前的信号与滤波后的干扰输出对消。

(3) 将对消后得到的信号做逆stretch处理即可恢复目标回波。

(4) 将恢复后的目标回波经过延迟处理与雷达接收机在第l+2个周期接收到的信号进行stretch处理，重复步骤(1)、(2)、(3)。

3 仿真实验及分析

3.1 算法的整体实现

仿真条件为：LFM信号的载频f0=10 MHz，带宽B=5 MHz，脉冲宽度τPW=5×10-5s，脉冲重复频率为10 kHz，调频斜率k=B/τPW；距离目标回波信号最近的假目标干扰的时延差Δτmin=5×10-6s；移频干扰产生导前假目标，移频量为fd=2MHz；自适应算法的迭代次数N=2 000；改变目标回波与干扰间的时延差，以间隔Δτ=5×10-6s的时延差产生8个假目标和1个导前假目标干扰。目标回波在假目标干扰下的对比图如图4所示。

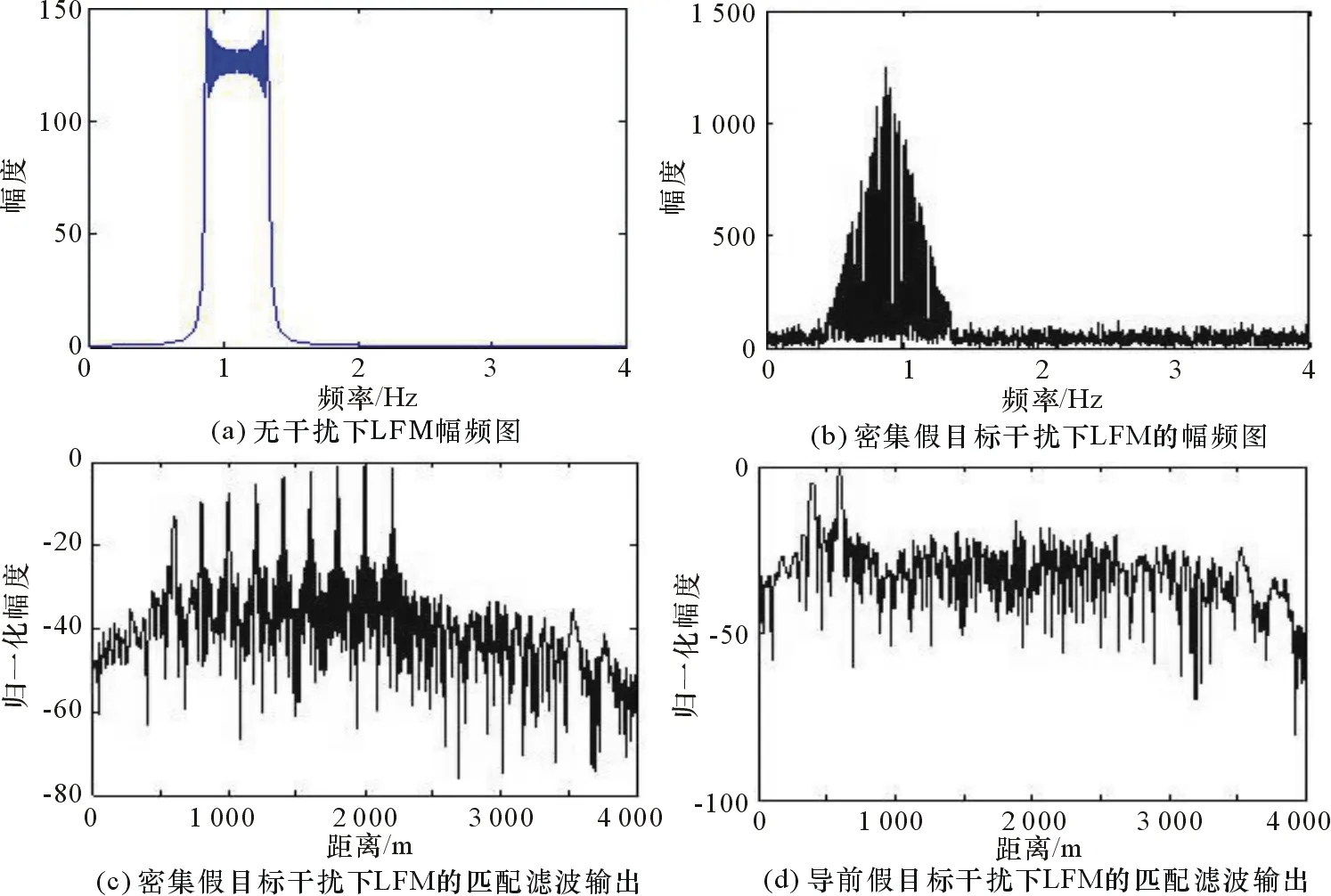
图4 目标回波在假目标干扰下的对比图

图4(a)和图4(b)分别为LFM信号在有无干扰情况下的幅频图，可以看出密集假目标干扰条件下，假目标干扰的频谱完全覆盖了目标回波。图4(c)和图4(d)分别为密集假目标和导前假目标干扰下LFM信号的匹配滤波输出，其中图4(c)中设置距离600 m处为真实目标，然后每间隔200 m产生8个距离假目标。图4(d)在距离400 m处通过移频处理产生一个导前假目标。可以看出干扰和目标回波都能与接收机匹配滤波，获得处理增益。因此，时域的匹配滤波无法判断真实目标的位置，且假目标干扰与目标回波的频谱间严重耦合。

图5为信噪比σSNR=0dB时，假目标干扰抑制前后对比图。图5(a)为假目标干扰下LFM信号的匹配滤波输出，其中距离600 m处为真实目标，每间隔200 m产生8个距离假目标，距离400 m处为导前假目标。图5(b)为逆stretch处理后信号的匹配滤波输出，可以看出仅在距离600 m处存在一个目标，有效抑制了导前假目标和密集假目标干扰。图5(c)为stretch处理后的信号频谱，可以看出目标回波与干扰经stretch处理后变为单频信号，此时，目标回波的频率为0.02 MHz，距离目标回波最近的干扰频率为0.52 MHz，同时导前假目标干扰的频率为39.52 MHz，因此，经stretch处理后的信号消去了二次项，从而得到频率不同的干扰及回波信号分量，实现了干扰分量与目标回波分量间的频域分离。图5(d)为自适应对消后的频谱，可以看出基于类箕舌线的变步长自适应滤波方法不仅可以抑制干扰，还可以消除背景噪声的影响。图5(e)为经逆stretch处理后的频谱，与图5(f)中LFM幅频图相比，可以看出本文所提方法在抑制背景噪声的同时有效抑制了多假目标干扰，并能良好地恢复回波信号。

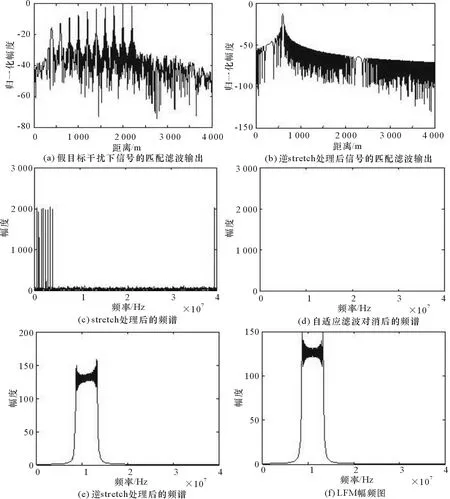
图5 假目标干扰抑制前后对比图

3.2 干扰抑制性能分析

在不同信干比下对本文所提方法的干扰抑制性能进行分析，其参数设置如下：干扰抑制前目标回波与每个假目标干扰信干比分别为σSJR=0 dB,-5 dB,-10 dB，其它参数与3.1相同。通过100次蒙特卡罗实验，得到干扰抑制后信干比随时延差的变化情况如图6所示。由图6可见，随着信干比的增大，其干扰抑制后信干比改善也增大。通常情况下，干扰抑制前的目标回波与每个假目标干扰信干比约为0 dB，在距离目标回波最近的干扰与目标回波之间的时延差为1×10-7s时，干扰抑制后信干比约为20 dB，因此，采用本文所提的改进变步长自适应滤波方法，在目标回波与干扰时延差较小时，也可有效地对回波信号滤波，干扰对消效果明显；在距离目标回波最近的干扰与目标回波之间的时延差大于4×10-7s时，干扰抑制后信干比约为33 dB，此时，本文所提的方法能更好地抑制密集假目标干扰。

图6 干扰抑制后信干比随时延差的变化情况

为了说明背景噪声对干扰抑制性能的影响，引入信干噪比[19]的概念。其中，信干噪比σSJNR=10lg[ps/(pj+σd2)]，其中ps和pj分别表示目标回波和干扰的功率，σd2为背景噪声的方差。参数设置如下：距离目标回波最近的干扰与目标回波之间的时延差τ=0.1,0.2,0.3,1 μs，干扰抑制前的目标回波与每个假目标干扰信干比为σSJR=0 dB，其它仿真参数与3.1相同。通过100次蒙特卡罗实验，得到信噪比的变化对干扰抑制性能的影响如图7所示。由图7可以看出，随着信噪比的增大，背景噪声对stretch处理中二次项去除以及自适应滤波的影响逐渐减小，干扰抑制后的信干噪比增大。结合图7的仿真可知，当τ>0.4 μs时，干扰抑制后信干比约为33 dB。因此，图7中τ3=0.3 μs及τ4=1 μs 2条折线几乎重合。当干扰抑制前信噪比大于-5 dB，τ>0.4 μs时，干扰抑制后信干噪比仍为33 dB。此时本文所提的方法在抑制多假目标干扰的同时，有效地消除了背景噪声的影响。

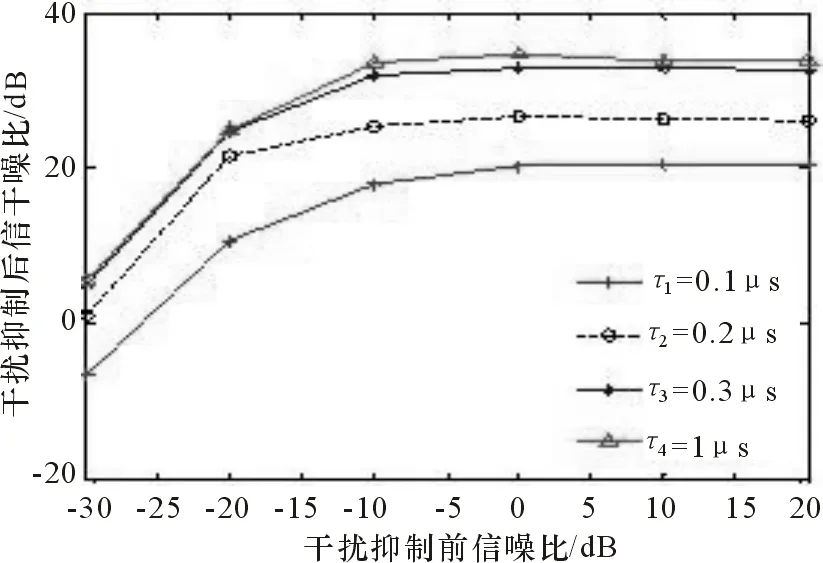
图7 信噪比的变化对干扰抑制性能的影响

接下来比较定步长自适应滤波器和本文提出的类箕舌线变步长自适应滤波器的滤波性能，其参数设置如下：干扰抑制前目标回波信号与每个假目标的干扰信干比分别为σSJR=0 dB，信噪比为-5 dB，迭代次数均为N=2 000，其它参数与3.1相同。通过100次蒙特卡罗实验，得到2种自适应滤波方法的干扰抑制性能比较如图8所示。

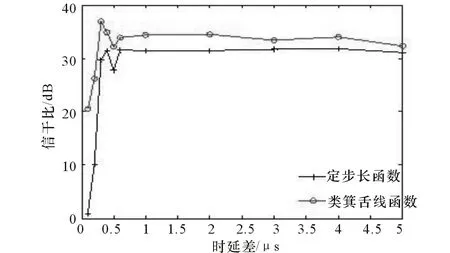
图8 定步长与变步长自适应滤波方法的干扰抑制性能比较

由图8可以看出，在距离目标回波最近的干扰与目标回波之间的时延差为1×10-7s时，采用基于类箕舌线函数的变步长(Proposed)自适应滤波方法干扰抑制后信干比约为20 dB，相比于定步长(Fixed)自适应滤波方法，干扰抑制后信干比不到1 dB；当时延差大于7.5×10-7s时，改进方法处理后信干比约为33 dB，而定步长自适应滤波方法处理后信干比约为30 dB。因此，当干扰与目标回波间存在较小时延差时，采用本文所提方法能更好地抑制密集假目标干扰。当干扰与目标回波之间的时延差很小时，导致对消后残留干扰的部分分量，使得恢复的回波信号中含有干扰分量；当时延差较大时，干扰抑制后信干比几乎不变。因此，随着时延差的增大，自适应滤波器的滤波性能逐渐稳定。当时延差为0.5×10-7s时，2种方法干扰抑制后的信干比出现极小值。

4 结束语

密集假目标干扰对LFM雷达产生较强的欺骗性，在时域以及频域上干扰与目标回波严重耦合，匹配滤波后很难区分真实目标与假目标。针对此问题，本文提出了一种类箕舌线函数的变步长自适应滤波方法，对stretch处理后的信号滤波，并对消滤波前后的密集假目标干扰。仿真结果表明，基于定步长的自适应滤波方法可有效地抑制干扰，但在干扰与目标回波间时延差较小时，其干扰抑制性能严重退化。本文提出的类箕舌线变步长自适应滤波方法可在干扰与目标回波间时延差较小时，更有效地对消干扰，消除了背景噪声的影响，且在目标回波与干扰高度耦合的条件下有效地抑制密集假目标干扰。

[1] 卢刚,唐斌,罗双才,等.LFM雷达中DRFM假目标自适应对消方法[J].系统工程与电子技术, 2011(8):1760-1764.

[2] 黎明也,曹志华,朱宝增,等.对线性调频雷达的密集假目标干扰研究[J].中国电子科学研究院学报,2014,9(3):272-276.

[3] 卢刚.雷达有源假目标抑制方法研究[D].成都:电子科技大学,2008.

[4] PACE P E,FOUTS D J,EKESTORM S,et al.Digital false-target image synthesizer for countering ISAR[J].IEE Proceedings——Radar, Sonar and Navigation,2002,149(5):248-257.

[5] 郝万兵，张军，谢敏.一种密集假目标干扰的建模及其仿真分析[J].火控雷达技术，2005(3)：76-78

[6] LIU Y,ZHANG G Y,HU X L,et al.Fast parameter estimation of LFM-PRBC signal under low SNR[J].Telecommunication Engineering,2014,54(10):1360- 1365.

[7] LU G,TANG B.Deception jammer rejection using pulse diversity in joint slow/fast-time domain[J].Journal of the Chinese Institute of Engineers,2013,36(3):405-410.

[8] SCHUERGER J,GARMATYUK D.Performance of random OFDM radar signals in deception jamming scenarios[C]//IEEE Radar Conference,2009:1-6.

[9] STANKOVIC L,DJUROVIC I,STANKOVIC S,et al.Instantaneous frequency in time-frequency analysis:enhanced concepts and performance of estimation algorithms[J].Digital Signal Processing,2014,35(3):1- 13.

[10]SCHIKORR M.High range resolution with digital stretch processing[C]//IEEE Radar Conference,2008:1-6.

[11]张克舟,李青山,张恒,于卫刚,等.LFM脉冲压缩雷达的随机移频多假目标干扰技术研究[J].电光与控制,2014,21(8):106-109.

[12]BERGER S D.Digital radio frequency memory linear range gate stealer spectrum[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(2):725- 735.

[13]WELSTEAD S.Characterization of diversity approaches for LFM stretch-processed waveforms[C]//International Waveform Diversity and Design Conference,IEEE,2007:418-422.

[14]董创业.基于DRFM的雷达干扰技术研究[D].西安:西安电子科技大学,2007.

[15]王淑艳,董健,关欣,等.基于自适应陷波技术的心电图工频干扰抑制研究[J].生物医学工程学杂志,2008,25(5):1044-1047.

[16]CHANDRA G V P,YADAV S,KRISHNA B A.Study of different adaptive filter algorithms for noise cancellation in real-Time environment[J].International Journal of Computer Applications,2014,96(10):20-25.

[17]CHEN Y,TIAN J,LIU Y.Variable step size LMS algorithm based on modified Sigmoid function[C]//International Conference on Audio,Language and Image Processing,IEEE,2014:627-630.

[18]HUAN Q Y,QIU X H,LIU X F.Variable step LMS algorithm using norm of the hyperbolic tangent function[J].Journal of Signal Processing,2014,30(1):93- 99.

[19]吴晓芳,卢焕章,代大海,王雪松,等.SAR有源相干干扰和非相干干扰功率分析[J].电子对抗,2009(1):1- 6.

Dense False-target Jamming Suppression Method Based on Improved Variable Step Size Adaptive Filtering

ZHOU Wen-hui1,MIN Bai-cheng2

(1.Unit 91404 of PLA,Qinhuangdao 066001,China;2.The 723 Instiute of CSIC，Yangzhou 225001，China)

This paper proposes a dense false target jamming suppression method based on improved variable step size adaptive filtering.Firstly,the stretch de-chirping technique is utilized to eliminate the quadratic term of the signal,and the target echo and jamming can be separated in the frequency domain,thus signal components with different frequencies could be obtained.Next,the variable step size adaptive filtering method based on Versiera-like function is applied to filter the stretch processed echo signal.Finally,the dense false target jamming is eliminated and the target echo is recovered through the application of inverse stretch processing to the eliminated signals.The presented adaptive filtering method based on Versiera-like function is applied to regulate the step size,which can effectively suppress the false target jamming which is close to the target echo.Simulation results show that the improved variable step size adaptive filtering method can effectively filter the echo signal and eliminate the jamming evidently when the time delay difference between the jamming and target echo is very small.Compared with the fixed step size filtering method,the proposed method still has a good robustness in the environment of low signal-to jamming ratio,and can effectively suppress the dense false target jamming.

dense false target;stretch processing;variable step size;adaptive filtering;jamming suppression

2016-06-16

TN973.21

A

CN32-1413(2016)05-0001-08

10.16426/j.cnki.jcdzdk.2016.05.001