水中振动矩形板的附加质量研究

任惠娟, 姚 展, 薛小庆, 刘 婷, 雷 烨



水中振动矩形板的附加质量研究

任惠娟1, 姚 展1, 薛小庆1, 刘 婷1, 雷 烨2

(1.咸阳师范学院 物理与电子工程学院， 陕西 咸阳 712000; 2.西北工业大学 航海学院， 陕西 西安 710072)

从水下振动矩形板的振动响应公式出发，根据附加质量的定义，推导了水下矩形板的附加质量表达式，并进行了数值仿真.研究表明：(1)模态阶数越低，矩形板附加面密度越大.(2)当波数比kw/kmnw<10-1时，矩形板的附加面密度与波数比无关而几乎保持恒值；当kw/kmnw≈1时，除过(1,1)阶模态，各阶模态附加面密度均出现了峰值；之后随着波数比的增大，模态附加面密度迅速衰减.(3)水下矩形板的附加质量不可忽略，研究水下结构的振动与声辐射必须考虑附加质量的影响.

矩形板； 附加质量； 附加阻尼

0 引言

当结构在重质流体中振动时, 由于流体与结构的相互耦合作用[1-6]而使其振动和声辐射变得复杂.流固耦合问题的弱耦合研究法[7]认为流体对结构的影响是以附加质量和附加阻尼的形式体现出来的, 因此围绕各种结构在流体中附加质量的研究很受人们的关注.王基盛等[7]采用弱耦合法分析了流体与结构的耦合作用，探讨了流体环境中影响结构附加质量的因素，并给出了流体动能的计算方法.钱勤等[8]借助Green公式，将结构附连水质量的计算化为一个边界积分，计算了水中圆柱体和球体的附连水质量.于丹竹等[9]通过建立带有附加质量主结构的有限元模型，将其与声流体介质的瑞利积分相互耦合以获得耦合系统的响应.马烨等[10]采用商用计算软件，运用Fluent非常定运动和动网格技术数值计算得到了物体六自由度运动的附加质量.刘莹等[11]在势流理论的基础上，求解了结构刚弹耦合的附加质量.李明等[12]通过建立水下航行体的梁模型，研究了其运动过程中附加质量的变化情况.以上研究针对不同水下结构采用不同方法研究了其附加质量问题，也从不同方面剖析了水下结构附加质量的产生机理，为求解结构在流体中的附加质量提供了很好的帮助.板结构是构成各种复杂结构的基本结构之一，本文则以水中点简谐力激励下的振动矩形板为研究对象，根据弱耦合研究理论, 对其振动响应公式进行修正，结合振动结构附加质量的定义，推导其附加质量的计算方法.本研究为进一步研究水介质对水下振动结构声辐射的影响奠定基础.

1 水中振动矩形板的振动响应

当结构在水中振动时，结构会向水中辐射声场，该声场将反作用于结构本身，从而对结构自身的振动和声辐射产生影响.声场对振动结构的影响体现在两个方面[7,13]：一方面由于结构的振动带动了周围流体的运动，这相当于振动结构自身的质量产生了增量，我们称之为附加质量; 另一方面，由于结构在振动的同时向周围的介质中辐射出声能量从而损耗了机械能，这部分能量的损耗可以用附加阻尼(又称为辐射阻尼)来进行描述.

设长为a、宽为b的矩形板置于水中，板的边界条件为四边简支并且被嵌于无限大障板中(如图1所示).当矩形板受到作用于点(x0,y0)处的简谐力Fejωt激励而发生振动时，考虑到振动过程中矩形板附加质量和附加阻尼的产生，将空气介质中点(x′,y′)的振速幅值表达式[14]中板的密度和阻尼分别进行修正，得到水下矩形板在点简谐激励下的振速幅值表达式为：

(1)

D为板的弯曲刚度.

图1 矩形板积分示意图

2 振动矩形板的附加质量

当矩形板受到作用于点(x0,y0) 处的简谐力Fejωt激励而发生振动时，面圆ds′的振动在ds处产生的声压幅值为

(2)

式(2)中:kw为水中声波波数，ρw为水的密度，cw为水中的声速.将(1)式代入(2)式并对整个辐射面进行积分，得到所有面元的振动在面元ds处产生的声压为

(3)

于是面圆ds受到声场的反作用力为

Fmnw(x,y)=Pmnw(x,y)·ds

(4)

面元ds的辐射阻抗为

(5)

面元ds的附加质量[13]为

(6)

由于板的振动，面圆的附加质量也随之一起振动，于是面元ds的附加质量对应的附加动能为

(7)

将(6)式代入(7)式并对(7)式积分，得到整个板面的附加动能为

(8)

从另一方面看，若令整个板面的(m,n)模态的附加质量为Δmmn，考虑到整个板面的振速均方值为

(9)

则整个板面的附加质量引起的整个板面的附加动能又可写为

(10)

于是由T′=T得

φmn(x,y)·φmn(x′,y′)ds′ds

(11)

(11)式即为水中振动矩形板(m,n)模态的附加质量表达式.

3 数值仿真

图2给出了边长为1 m的四边简支方板前9阶模态的附加面密度随着波数比的变化情况.图中横坐标为辐射声波的波数kw和矩形板(m,n)阶模态弯曲波波数kmnw的比值，即波数比.

图2表明，在双对数坐标系下，水中简支边界方板的附加面密度随波数比的变化关系呈现出以下特点：

(1)模态阶数越低，方板附加面密度越大.

(2)当kw≪kmnw时，方板各阶模态的附加面密度曲线近似为与横轴平行的直线，即方板的模态附加面密度几乎与波数比无关.

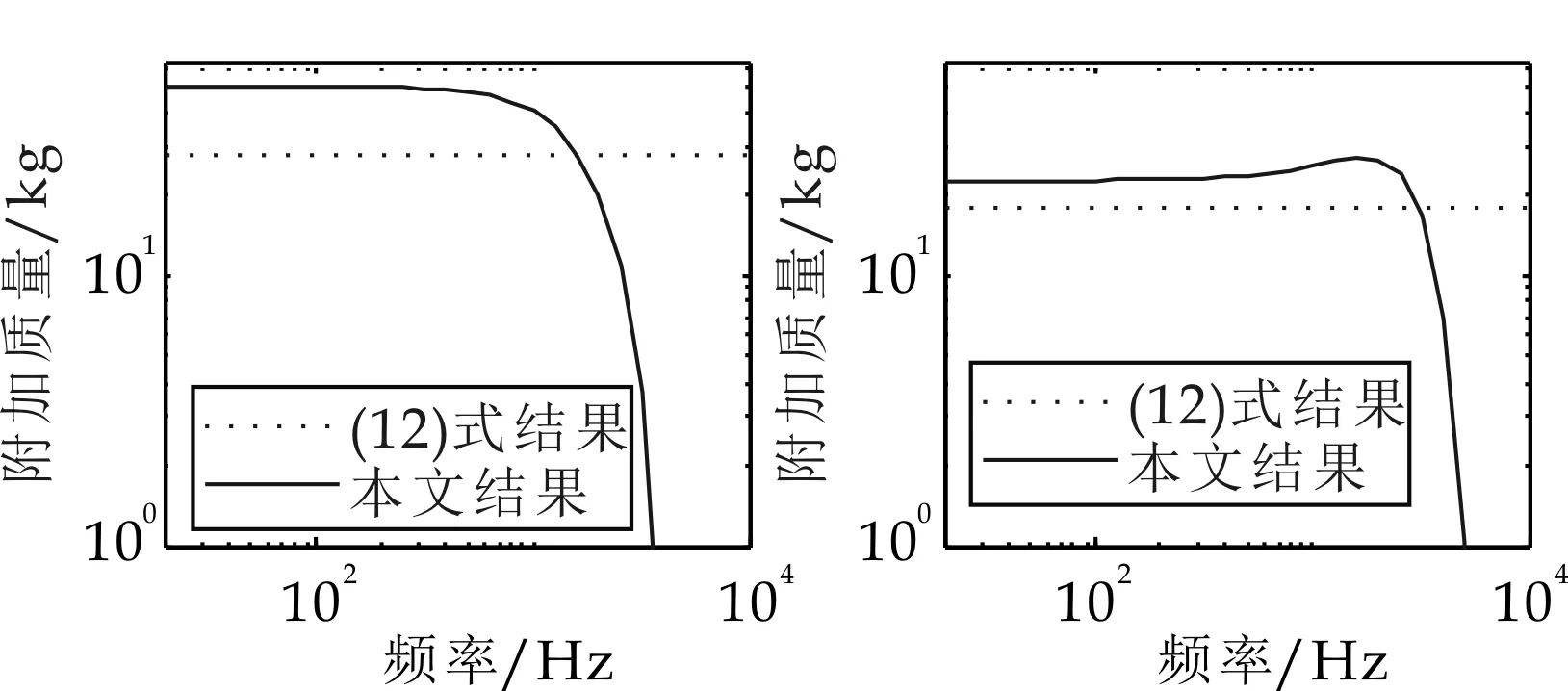
(3)当kw

(4)当kw≈kmnw时，除(1,1)模态外，各模态的附加面密度均出现峰值，且模态阶数越高，峰值越明显.

(5)当kw≫kmnw时，所有模态的附加面密度均迅速减小.

图2 简支边界矩形板前9阶模态的附加面密度

图3给出了边长为1 m的方板在简支边界条件下单面临水及在空气中的附加面密度对比情况.

由图3可以看出，当方板在水中振动时，其附加面密度远远大于其在空气中的情形.另外，对于边长为1 m、厚度为6 mm的钢质方板在空气中振动时，计算表明，其附加面密度远在1 kg/m2数量级以下，远远小于方板自身的面密度(约为47 kg/m2).这说明在空气介质中计算板的振动及声辐射时由于振动板的附加质量远远小于自身质量，因而可以完全不考虑其附加质量的影响.而当该板在水中振动时，其附加面密度在102kg/ m2数量级左右，远大于或接近于其自身的面密度，所以当板在水下振动时，必须考虑其附加质量的影响.

(a) (1,1)模态 (b) (6,3)模态

(c) (4,4)模态 (d) (3,2)模态图3 简支边界方板在空气及水中的附加面密度对比

4 本文附加质量与波数变换法附加质量计算结果对比

文献[15]用波数变换法推导出了临界频率以下频段简支边界矩形板的附加质量,其表达式为：

(12)

文献[15]同时指出，这一表达式适用于计算较高阶模态矩形板的附加质量，当其用于计算较低阶模态的附加质量时将会有较大的误差.这里以边长为0.5 m的方板为例，将本文方法的低阶模态计算结果(如图4所示)及高阶模态计算结果(如图5所示)分别与上式计算结果进行对比.

对于图4的各低阶模态，本文的计算结果均高于(12)式的计算结果，尤其是对于(1,1)阶模态，本文的结果远远高于(12)式的结果.但是图4也表明随着模态阶数的逐步升高，本文的计算结果越来越接近于(12)式的计算结果.对于图5的各高阶模态，本文的计算结果与(12)式的结果一致性良好.

(a) (1,1)模态 (b) (1,2)模态

(c) (1,3)模态 (d) (2,2)模态图4 低阶模态附加质量对比

(a) (4,5)模态 (b) (5,6)模态

(c) (6,7)模态 (d) (7,7)模态图5 高阶模态附加质量对比

以上对比结果与文献[15]中指出的(12)式适用范围相吻合.由于(12)式在推导的过程中做了一定的近似处理，这种近似对于高阶模态是适合的，但对于低阶模态则不适用[15]，因此(12)式仅适用于计算高阶模态的附加质量.本文给出的矩形板附加质量计算公式(11)式是根据弱耦合理论严格推导得到的.(11)式和(12)式是在不同的物理模型下推导的结果，其高阶模态计算结果良好的一致性则表明了本文物理模型的有效性及推导结果正确性.另外，从仿真结果上看，对于低阶模态，随着模态阶数的逐步升高，两种计算结果的差别有逐渐缩小的趋势，到了高阶模态时则达到了完全一致的地步，而这恰恰是(12)式推导过程中所做的近似处理更适用于高阶模态的具体反映.因此，不仅由该模型所推得的高阶模态附加质量计算结果是正确的，而且其低阶模态附加质量计算结果也是可信的.

本文的附加质量计算方法由于既可用于计算高阶模态，又可用于计算低阶模态，因此较(12)式适用范围更广.

5 结论

本文从修正后的水下矩形板振动响应公式出发，推导了其附加质量表达式，并根据该表达式进行了数值仿真，结果表明：(1)模态阶数越低，矩形板附加面密度越大.(2)当波数比kw/kmnw<10-1时，矩形板的附加面密度几乎保持恒值而与波数比无关；随着波数比的增大，附加面密度逐渐波动变化；当kw/kmnw≈1时，除过(1,1)阶模态，其他模态的附加面密度均出现了峰值；之后随着波数比的增大，附加面密度迅速衰减.(3)水下矩形板的附加质量不可忽略，研究水下结构的振动与声辐射必须考虑附加质量的影响.

[1] 沈惠明,赵德有.流固耦合振动问题的特征值解法[J].大连理工大学学报,1990,30(3):369-371.

[2] 吴 芳,赵德有.水对船舶与海洋建筑物结构振动影响的研究[J].中国海洋平台,2007,22(3):22-26.

[3] K.H.Jeong.Free vibration of two identical circular plates coupled with bounded fluid[J].Journal of Sound and Vibration,2003,260:653-670.

[4] K.H.Jeong,K.J.Kim.Hydroelastic vibration of acircular plate submerged in a bounded compressible fluid[J].Journal of Sound and Vibration,2005,283:153-172.

[5] Kyeong Hoon Jeong,Gyu Mahn Lee,Tae Wan Kim. Free vibration analysis of a circular plate partially in contact with a liquid[J]. Journal of Sound and Vibration,2009,324:194-208.

[6] Kenneth D.Frampton.Radiation efficiency of convected fluid-loaded plates[J].J.Acoust.Soc Am,2003,113(5):2 663-2 673.[7] 王盛基,杨庆山.流体环境中结构附加质量的计算[J].北方交通大学学报,2003,27(3):40-43.

[8] 钱 勤,黄玉盈,刘忠族.求附连水质量的一种直接方法[J].力学与实践,1996,18(5):19-21.

[9] 于丹竹,黎 胜.附加质量对于水中平面板振动噪声特性的影响[J].舰船科学技术,2015,37(6):26-29.

[10] 马 烨,单雪雄.数值计算复杂外形物体附加质量的新方法[J].计算机仿真,2007,24(5):75-78,113.

[11] 刘 莹,杨 衡,王毅娜,等.三维结构水中刚弹耦合运动附加质量特性分析[J].江苏船舶，2014,31(5):5-9.

[12] 李 明,尹云玉.水下航行体动态响应计算的附加质量探讨[J].导弹与航天运载技术,2008(4):16-18.

[13] 杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2001.

[14] G.Xie,D.J.Thompson,C.J.C.Jones.The radiation efficiency of baffled plates and strips[J].Journal of Sound and Vibration,2005,280:181-209.

[15] Fahy F.Sound and structural vibration:Radiation,transmission and response[M].London:Academic Press,1985.

【责任编辑：蒋亚儒】

Study on the attached mass of the rectangular plate in water

REN Hui-juan1, YAO Zhan1, XUE Xiao-qing1, LIU Ting1, LEI Ye2

(1.College of Physics and Electronic Engineering, Xianyang Normal University, Xianyang 712000, China; 2.College of Marine, Northwestern Polytechnical University, Xi′an 710072, China)

Starting from the vibration response formula of the rectangular plate in water and according to the definition of the attached mass,the expression of attached mass is derived for a rectangular plate in water,and the numerical simulations are implemented.The results show:First, the lower the modal order,the bigger the attached mass.Second, whenkw/kmnw<10-1,the attached mass almost keeps a constant value.Whenkw/kmnw≈1,the attached mass appears a peak value except the (1,1) mode,then it decays fastly.Third,the attached mass of the rectangular plate in water can not be neglected,and it should be taken into account when vestigating its vibration and sound radiation.

rectangular plate; attached mass; attached damping

2016-09-27

陕西省科技厅自然科学基金项目 (2011JM1017); 陕西省教育厅科学研究计划项目(2013JK0618)； 咸阳师范学院专项科研基金项目(13XSYK016)

任惠娟(1972-)，女，陕西周至人，副教授，博士，研究方向：结构振动与声辐射

1000-5811(2016)06-0183-04

O422.6

A