多线切割机张力控制系统的分析与校正

吴 旭，姜家宏，田洪涛，张为强

(中国电子科技集团公司第四十五研究所，北京100176)

多线切割机张力控制系统的分析与校正

吴 旭，姜家宏，田洪涛，张为强

(中国电子科技集团公司第四十五研究所，北京100176)

针对原多线切割机设计中控制系统稳定性差的问题，建立了张力控制系统的模型，分析了钢丝拉伸变形对于控制系统稳定性的影响，提出了新的用于产生钢丝张力的伺服电机的转矩控制方案，并通过理论分析和实际使用证明，改进后的控制方法有效提高了张力控制系统的稳定性，满足了设备的使用要求。

多线切割机；张力控制；稳定性；极点

多线切割机是一种用于半导体材料及脆硬材料切割的设备，和传统的切片机相比，多线切割机具有生产效率高、材料损耗少的优点，同时，所加工的硅片具有弯曲度小、翘曲度小、表面损伤层浅及表面粗糙度值小等优点，是目前半导体材料加工的关键设备。但同时，多线切割机也是一种复杂的设备，对控制系统的稳定性、可靠性及实时性都有很高的要求，而张力控制系统更是多线切割机控制系统的核心技术，是设备的稳定工作和保证材料加工质量的关键。

张力控制机构广泛应用于材料加工、纺织、造纸及印刷等行业中，张力控制系统具有时变性、非线性及强扰动等特点[1，2]，是工业自动化系统中常见的典型控制系统，也是多线切割机设计中的难点。在多线切割机材料加工过程中若张力控制系统出现故障，造成张力波动过大甚至钢丝断线，会给用户造成较大的经济损失。因此，张力控制技术也是确保多线切割机能够稳定工作的一项关键技术。

1　多线切割机的总体结构

多线切割机的总体结构如图1所示，主要包含了工作台及送料机构、轴辊、收/放线轮、浮辊式张力缓冲机构及相关机构的驱动电机。其中驱动轴辊的电机采用主轴电机，收/放线轮驱动电机采用高动态性能的伺服电机，并分别由变频器或伺服驱动器控制其转速。浮辊式张力缓冲机构由施加张力的伺服电机直接驱动，通过控制伺服电机的转矩来调节钢丝的张力，同时可以通过电机编码器的反馈值测量张力缓冲机构的摆动角度。而工作台由伺服电机驱动，实现送料装置的上下运动。此外，多线切割机还包括线轮布线系统及相关的传感器及温度控制系统等辅助装置。

在设备工作时，首先按照工艺要求由砂浆泵以一定的流量向轴辊区域喷射砂浆，钢丝以螺旋形式缠绕在轴辊上，并且按照切割工艺要求轴辊单向或往返运动，并由收/放线轮同步转动，保证钢丝的持续供给和回收，同时通过伺服电机驱动张力缓冲结构给予钢丝施加一定的张力。工作台驱动的伺服电机使夹持的待切硅棒向下运动，由轴辊区间的钢丝线网带动砂浆对被切材料进行磨削加工，实现对材料的切割。

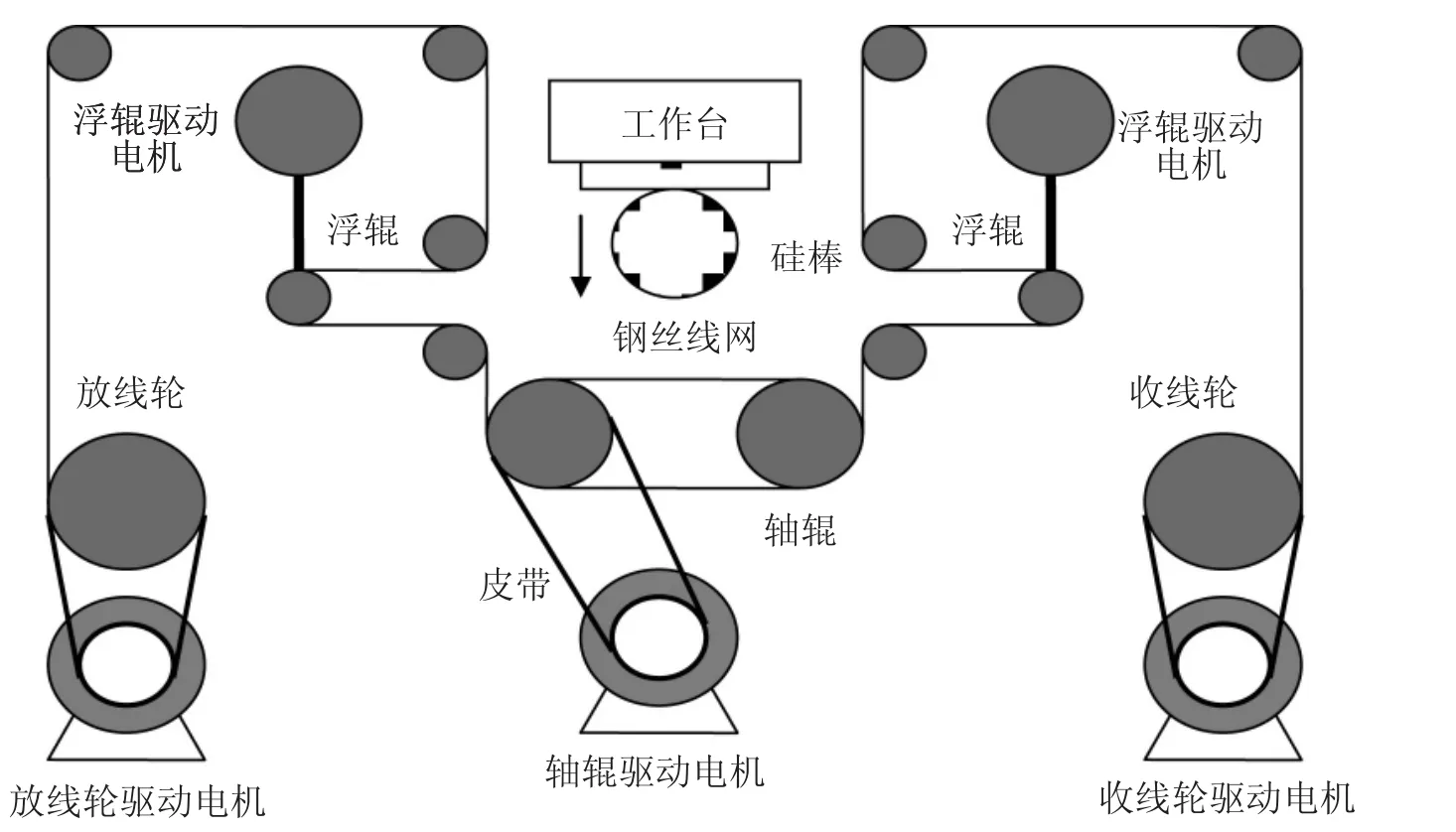
图1　多线切割机总体结构示意图

2　张力控制系统的模型及分析

图1所示的张力控制系统中，通过伺服电机采用力矩控制方式驱动浮辊，对钢丝施加一定的张力，在设备工作过程中，实时检测浮辊的转角，并反馈至控制系统中用于调整收放线轮驱动电机的转速。由于本系统的浮辊与其驱动电机是直连的，因此可以通过检测伺服电机的编码器脉冲数来测量浮辊的转角。

浮辊张力调节机构的示意图如图2。

浮辊的一端O0固定在基板上，并且与伺服电机相连，在设备工作时浮辊以O0为中心摆动，通过分析[3]可知，当轴辊的线速度V0与收/放线轮的线速度V1，不相等时，浮辊的摆角θ将发生变化，并且满足如下关系：

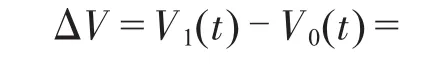
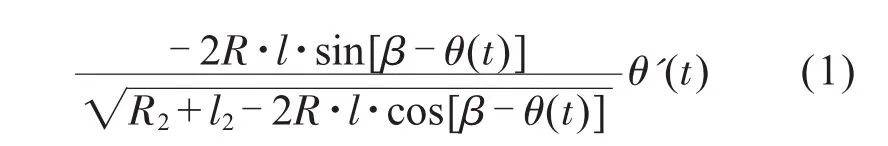
图2　浮辊张力调节机构示意图

其中：R为浮辊固定点到两导轮中心点P的距离，l为浮辊的长度，V0(t)是轴辊的线速度，而V1(t)是收/放线轮的线速度，而β是与设备机械结构有关的固定值。

在设备实际工作过程中，浮辊通常在以垂直方向为平衡位置附近摆动，θ(t)≈0，因此β-θ(t)≈β，并且在浮辊处于垂直方向中心位置时，O1P也与其垂直，根据几何关系，公式(1)可以简化为：

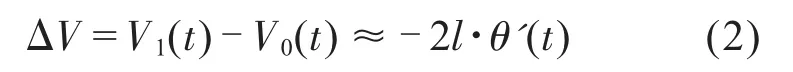
上述公式(1)和（2）是将钢丝作为刚性体来考虑的，实际上由于多线切割机所用的切割线非常细（φ0.1～φ0.2 mm），在浮辊施加张力和摆动过程中由于钢丝所受张力的变化，使得工作区间的钢丝长度发生变化，并引起浮辊摆动角度发生变化。因此，需要根据钢丝的变形情况对上述公式进行修正。

当对钢丝施加张力时，钢丝将发生变形，钢丝长度伸长，引起浮辊摆动角度发生变化。在浮辊处于平衡位置附近且变形量不大时，由于钢丝变形引起的浮辊摆角变化与钢丝张力之间的关系可以表示为：

其中：η为钢丝受到张力拉伸变形引起的浮辊摆角变化量，F为钢丝所受到的张力，而γ为与材料和设备相关的变形系数。

在设备工作时，伺服电机输出转矩M控制浮辊对钢丝施加一定的张力，而在钢丝运动过程中，由于摆动角度θ(t)的变化，引起钢丝所受到的张力F发生变化，根据力矩平衡的关系可以得到：

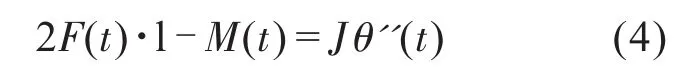
由公式(3)和(4)可以得到由于钢丝张力变化引起的浮辊摆角变化量为：

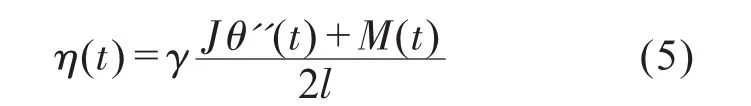
因此，考虑到钢丝张力变形的影响后，因在原公式(2)中由于在V1(t)与V0(t)之差引起的浮辊角度变化量的基础上减去钢丝变形引起的浮辊角度变化量，得到实际的浮辊摆动角度。对公式(2)进行修正后取拉氏变换，并且假设系统初始状态为零，整理后得到：

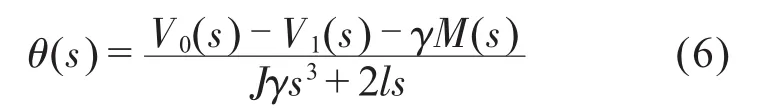
设备在工作时采用前馈与PI控制方式调整收/放线轮的速度V1(t)：

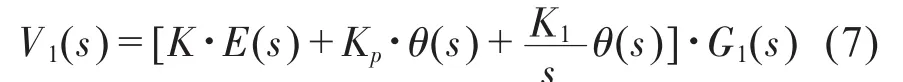
其中E(s)为程序设定的轴辊线速度工作曲线，由运动控制系统按照工艺要求预先设置，G1(s)为收/放线轮电机驱动系统的传递函数，K、Kp与Ki分别为前馈控制系数、比例系数与积分系数，由于在控制系统中是通过调节收放线轮电机的转速V1(s)来控制浮辊的摆角，而轴辊线速度V0(s)和对于浮辊机构施加的转矩都是由程序预先设置的，在分析控制系统稳定性时可以省略，仅考虑线轮速度的影响，于是由公式(6)、(7)可以得到如图3所示的控制系统模型。

由图3所示的方框图可知，系统开环传递函数为：

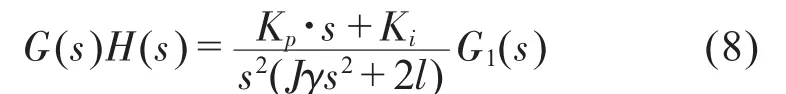
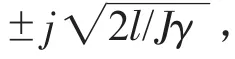
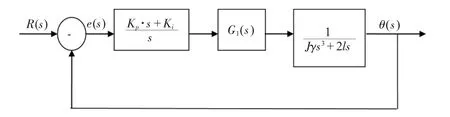
图3　张力控制系统方框图

如果将钢丝看做刚性体，忽略其变形产生的影响（即γ=0），此时收/放线轮速度与浮辊摆角之间为一简单的积分环节，采用适当的PID控制参数时系统可以稳定，但是实际上由于γ≠0，对于控制系统的稳定性产生了影响，而且钢丝越细，工作长度越长，则变形系数γ越大，对张力控制系统稳定性的影响也越大，因此不能忽略其对张力控制系统的影响。

按照原设计采用的控制方案在实际工作过程中，设备运行初期尚未出现较大问题，但是当设备运行一段时间后，经常出现钢丝断线的情况，且故障出现时无明显征兆，设备各子系统也工作良好，重新对系统的控制模型进行分析后，初步确定是由于钢丝变形对于设备稳定性造成的影响，引起控制系统稳定性下降，并且分析在设备工作初期未出现明显的稳定性问题是由于设备工作初期浮辊系统等运动部件未经过磨合，摩擦系数较大，由于摩擦产生的阻尼作用缓解了设备的稳定性问题，但是随着设备工作时间加长，各系统部件的磨合，摩擦系数减小后设备的稳定性逐渐变差并出现钢丝断线的情况。

3　张力控制系统的校正

为满足张力控制系统稳定性的要求，必须对控制系统进行改进和校正。改进的思路主要是考虑到原系统的稳定性主要是由于钢丝变形造成的，在钢丝变形时，钢丝-浮辊机构成为储能元件，如果存储的能量不能及时释放，可能对设备的稳定性造成影响，如果能够在控制系统中添加阻尼元件，增加钢丝-浮辊装置中存储的能量损耗，就有可能提高设备的稳定性，满足控制系统的稳定性要求。

由于原设计机械结构的限制，添加阻尼器等控制元件非常困难，为此，我们考虑对原施加张力的伺服电机的控制方式进行改变。原系统中该伺服电机根据设备工艺要求在设备工作过程中输出固定的转矩M，在设备运行过程中转矩不做任何变化与调整。改进后，该伺服电机的输出转矩变为：

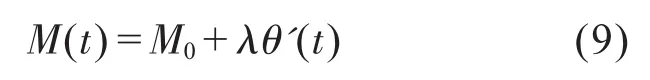
即在原固定转矩之上叠加一与浮辊摆动角速度有关的转矩，通过转矩控制系统的实时调整构成一阻尼装置。

将公式(9)进行拉氏变换并代人公式(6)中，整理后得到：

由公式(7)及(10)，并忽略轴辊速度V1(s)等与系统稳定性无关的因素后，得到改进后的张力控制系统，见图4所示。

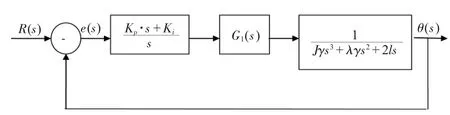
图4　改进后的张力控制系统方框图

由图4所示的方框图可知，系统开环传递函数为：

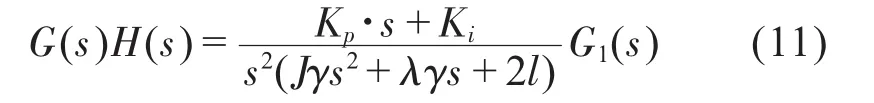
系统在原点具有一个二阶极点，以及一个零点，另外还包括一个二阶振荡环节，以及收放线轮电机驱动系统传递函数G1(s)确定的零极点。

对于二阶振荡环节，可以求出其包含的极点为：

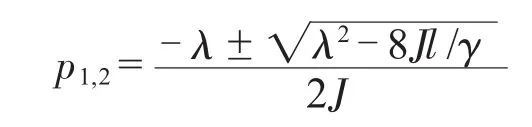
浮辊的转动惯量J、浮辊长度l是由机械结构确定的，而根据目前工艺要求确定了钢丝材料与直径后，钢丝变形系数γ也是确定的，对于电气控制系统而言，只能通过调整阻尼系数λ来调整二阶振荡系统的极点位置。

根据上述二阶振荡系统极点的计算公式可知：

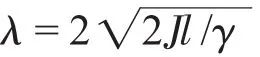
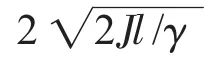
在求的二阶系统的极点位置后，并按照控制系统稳定裕度的要求，设定控制系统的剪切频率为：ωc=10，设置控制系统的零点位置为：z=-Ki/Kp=-1，并由公式(11)可以确定PI控制器的参数为：Kp= Ki=6.6。

确定上述控制系统参数后，可以得到所设计的张力控制系统的开环传递函数为：

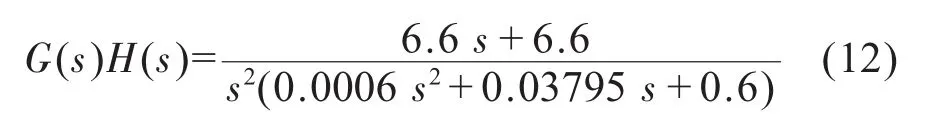
由公式 (12)确定的控制系统全部开环极点位于s平面左半部（包括原点处的极点），用MATLAB软件绘制出其频率响应Nyquist曲线如图5所示[4]，需要说明的是，由于系统开环传递函数中包含有s平面原点处的极点，因此应在图5所示的Nyquist曲线中增补由ω=0-到ω= 0+沿半径为无穷大的顺时针圆弧[5]。显然，图 6所示的Nyquist曲线未包含(-1，j0)点，该控制系统是稳定的。

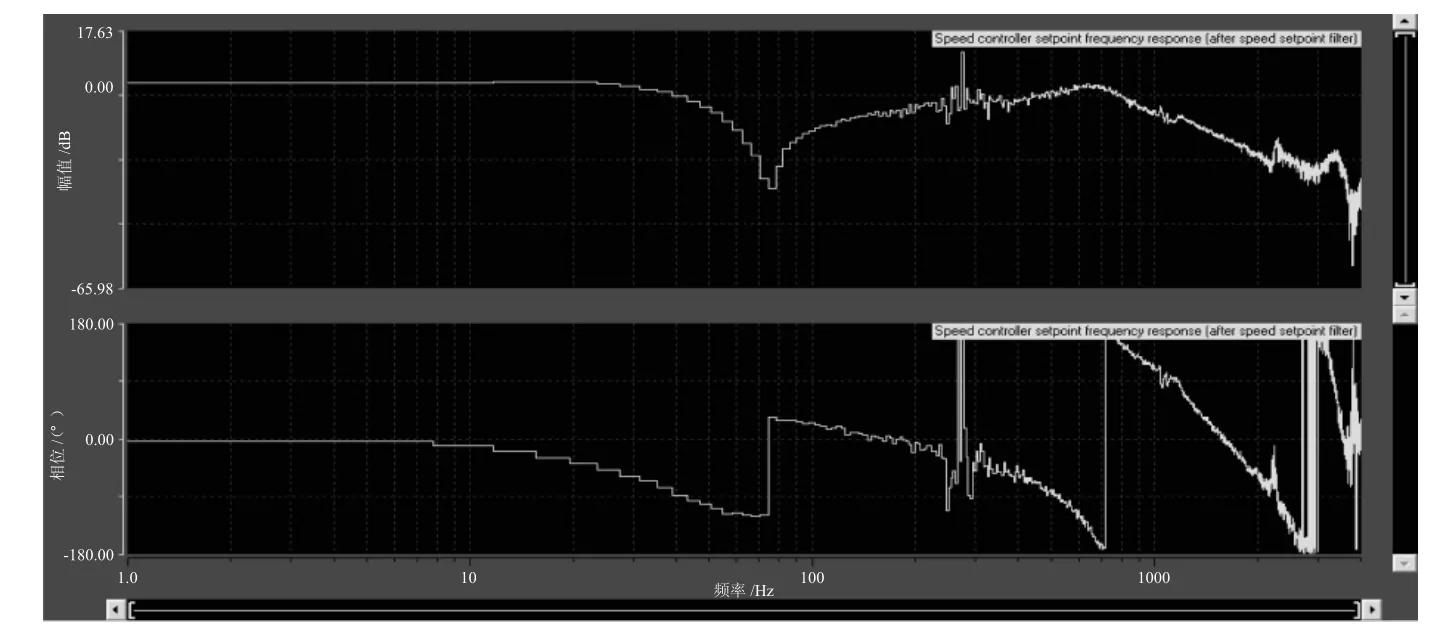
图5　线轮电机速度环波特图

张力控制系统频率响应的Bode图见图7。

根据图6可知，上述控制系统的相位稳定裕度为46.2°，幅值稳定裕度为12.4 dB，满足控制系统稳定性的要求。

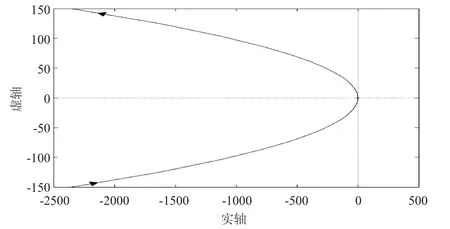
图7　张力控制系统的Bode图

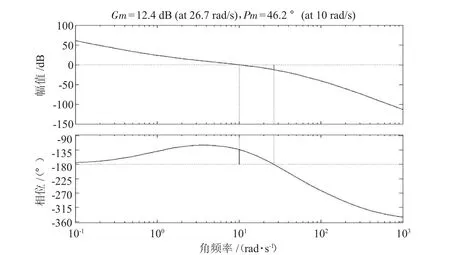
图6　张力控制系统开环频率响应的Nyquist曲线

5　结束语

经改进后，多线切割机张力控制系统经过了用户多次工艺试验、考核和验收工作，设备工作稳定可靠，从未因电气控制系统的问题造成钢丝断线、设备停机等故障，证明我们对张力控制系统的分析和改进工作是有效的。

[1]G.F.Franklin，J.David Powell.Michael Workman，DigitalControl of Dynamic Systems[M].Addison Wesley，1998.

[2]郭帅，何永义，姚志良，等.张力控制试验平台及监测系统的研究[J].工业仪表与自动化装置，2005，(4)：38-41.

[3]吴旭.高速浮辊张力控制系统的研究[J].电子工业专用设备，2007，36(11)：5-7.

[4]黄忠霖.控制系统MATLAB计算及仿真[M].北京：国防工业出版社，2004.

[5]李友善.自动控制原理[M].北京：国防工业出版社，1989.

Analysis and Correction of Tension Control System for Multi Wire-Saw

WU Xu，JIANG Jiahong，TIAN Hongtao，ZHANG Weiqiang
(The 45thResearch Institute of CETC，Beijing 100176，China)

Aimed at improving the stability of original designed tension control system for the multi wire-saw，a model of the tension control system is established and the effect of steel wire's elongation to the system stability is analysed.A new torque controlling method of the servo motor to generate the tension of wire is put forward.The theoretic analysis and practical use of this way has proved that the improved tension control method enhance the stability of the tension control system effectively and the tension control system meet the requirement of the device.

Multi wire-saw；Tension control；Stability；Pole point

TN305

B

1004-4507(2016)11-0011-06

2016-10-19

项目来源：国家02科技重大专项“硅材料设备应用工程”（2009ZX02011-002A）支持项目。

吴旭（1975-）男，硕士研究生，高级工程师，现从事精密测量及运动控制技术研究。