高考中常见的集合问题
2016-12-12山东省东营市广饶第一中学缪永春
山东省东营市广饶第一中学 缪永春
高考中常见的集合问题
山东省东营市广饶第一中学缪永春
集合的概念和运算是历年高考的必考内容.部分同学对于集合的内容掌握不牢固、理解不透彻,导致高考失分.
高考集合概念运算
集合的概念和运算出题形式灵活多样.部分同学对于集合的内容掌握不牢固,犯了不该犯的错误.关于集合在解题中经常出现的问题总结如下:
问题一:概念理解不清
例题1:已知集合A={直线},集合B= {圆},则A∩B=().
A.空集B.{圆}C.{直线}D.{两个点}
错解:选D
分析:本解法的错误在于对于集合的概念理解不清,即集合A∩B表示集合A与集合B中的共同元素而不是两个集合表示图形的相交部分.
正解:因为集合A的元素是直线图形,集合B的元素是圆的图形,显然没有相同的图形,
所以集合A∩B为空集.
问题二:忘记元素的性质
例题2:已知x2∈{0,1,x},求实数x的值.
错解:当x2=0时,解得x=0;
当x2=1时,解得x=±1;
当x2=x时,解得x=0或x=1,所以x的值为0,-1,1.
分析:本解法的错误在于仅仅是抓住了元素与集合的关系求解,而没有考虑集合中元素的性质导致出现错误.
正解:因为x2∈{0,1,x}=A,所以当x2= 0时,解得x=0,此时A={0,1,0}不成立.
当x2=1时,得x=±1,当x=-1时,A= {0,1,-1}成立,x=1时,A={0,1,1}不成立.
当x2=x时,解得x=0或x=1.当x=0时,A={0,1,0}不成立,x=1时,A={0,1,1}不成立.
所以x的值为-1.
问题三:集合的描述法理解不透
A.A哿BB.B哿A
C.A=BD.以上都不对
错解:选C.
分析:本题结论错误的原因在于对于集合的描述法的表示不能正确理解,即没有注意到集合A、B的代表元素的意义.
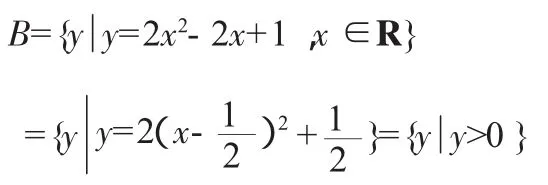
所以B哿A.故选B.
问题四:集合的特点把握不牢
所以ax-2=0的解是负数
分析:本解法错误的原因在于忽视了集合A为空集的情况,由A∩B=覫可知集合A为空集或A中的元素为负值.
当ax-2=0无解时,即a=0;
所以a≤0.
问题五:忽视题目的隐含条件
分析:本题的解法存在两处问题:一是B哿A说明集合B可以是空集;二是m+1≤x≤2m-1成立说明2m-1≥m+1.
正解:由于B哿A,所以当B为空集时,2m-1
