基于小波变换的智能天线波束形成算法

李 娜,殷兴辉,高文昀

(1.宿州学院 机械与电子工程学院,安徽 宿州 234000; 2.河海大学 计算机与信息学院,江苏 南京 211100)



·信息科学·

基于小波变换的智能天线波束形成算法

李 娜1,2,殷兴辉2,高文昀2

(1.宿州学院 机械与电子工程学院,安徽 宿州 234000; 2.河海大学 计算机与信息学院,江苏 南京 211100)

提出一种基于小波变换的智能天线波束形成算法(WL-SMILMS)。该算法采用小波函数将夹杂干扰噪声的来波信号变换在多尺度频域，对高频部分采用采样矩阵求逆算法(SMI)进行权矢量更新，对低频部分采用最小均方误差算法(LMS)进行权矢量更新,用两部分融合后的权矢量更新滤波器抽头权值,实现数字波束形成。该算法克服了SMI算法计算复杂度高、旁瓣偏高的缺点,比LMS算法具有更好的收敛性,实现了收敛率和计算复杂度的高度兼顾。

数字波束形成;小波变换;智能天线;采样矩阵求逆算法；最小均方误差算法

传统的智能天线波束形成算法有最小均方误差算法(LMS)和采样矩阵求逆算法(SMI)。最小均方误差算法具有简便灵活、易于实现、稳定性高的优点,但收敛速度较慢[1]。由于电磁环境的复杂性和日益增长的使用需求,现代电子测量装备需要比传统的探测设备具有更好的快信号目标侦测能力。因此,收敛速度较慢的最小均方误差法的应用受到了限制[2]。采样矩阵求逆算法虽然收敛速度较快、数值特征稳定、抗干扰效果较好,但是计算复杂度较高,当采样较少时,波束图主瓣容易畸变、副瓣过高。主瓣畸变降低了获取期望信号的准确性,副瓣过高则降低系统对干扰信号的抑制力[3]。

因此本文提出一种基于小波变换的智能天线波束形成算法(WL-SMILMS),实现收敛率和计算复杂度高度兼顾，满足在复杂性电磁环境里精确获取目标的需求。

1 智能天线波束形成算法

1.1 基本原理

智能天线由天线阵、模数转换、波束形成网络和自适应数字信号处理这4部分构成[4],如图1所示。

图1 智能天线原理框图Tab.1 Block diagram of smart antenna

假设期望信号Sk(t)从Qk方向入射,干扰信号Sj(t)共J-1个,从Qj方向入射。阵元接收信号矢量可表示为[5]

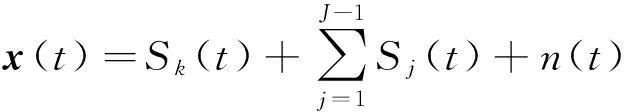
(1)

Sk(t)=sk(t)·V(Qk)，

Sj(t)=sj(t)·V(Qj)。

(2)

n(t)为噪声,V(θ)为信道中的阵元响应。经加权,天线阵的输出可表示为[6]

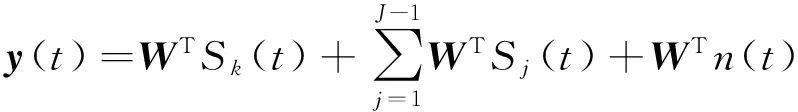
(3)

智能天线波束形成算法的核心就是如何确定最佳权矢量W， 从而提取期望信号、 抑制干扰信号和滤除噪声信号。 经典的算法有最小均方误差

算法(LMS)和采样矩阵求逆算法(SMI)[7]。

1.2 最小均方误差算法

最小均方误差算法的性能函数为

ξ=E{|e(n)|2}=E{e(n)e*(n)}=

E{|d(n)|2}-WHrxd-

(WHrxd)*+WHRxxW=

E{|d(n)|2}-2Re{WHrxd}+WHRxxW。

(4)

若要ξ取最小值,W应满足

(5)

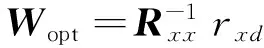
(6)

现通过梯度搜索求解此式。

(7)

μ为步长因子。将式(5)带入式(7)可得

W(n+1)-Wopt=(I-2μRxx)[W(n)-Wopt]。

(8)

用瞬时平方误差|e(n)|2代替均方误差ξ=E{|e(n)|2},代入式(7)可得

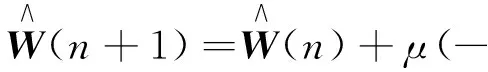
(9)

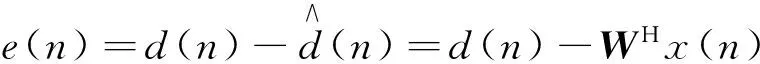
(10)

由式(9)可得LMS算法递推公式[8]

(11)

假设来波信号包括期望信号、干扰信号1和干扰信号2,其参数如表1所示。

表1 信号的各项参数值

计算机仿真LMS算法方向图如图2所示。算法采用直线阵,天线阵元为18,实现了主瓣指向20°,在40°和60°产生零陷。设M为自适应横向滤波器的抽头数目,LMS算法在一次迭代中只需要进行2M+1次乘法和2M次加法,计算复杂度记为O1(M)。可见,LMS算法具有简便灵活、易于实现、稳定性高的优点,但计算机运行LMS算法时间为0.161～0.173s,收敛速度较慢,导致在雷达追踪动态目标的应用上受到限制[9]。

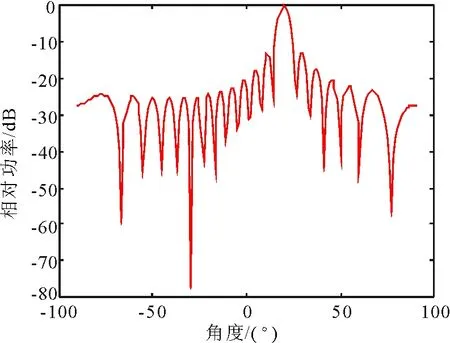
图2 LMS算法方向图Fig.2 Array beam patterns of LMS

1.3 采样矩阵求逆算法

采样矩阵求逆算法根据估计的采样协方差矩阵求逆计算权矢量,最优权矢量表达式为

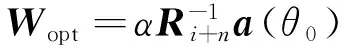
(12)

式中，Ri+n为干扰噪声的协方差矩阵,a(θ0)为期望信号的导向矢量值。因为信号、干扰、噪声往往是先验未知的,Ri+n只能通过采样,再利用最大似然估计为

(13)

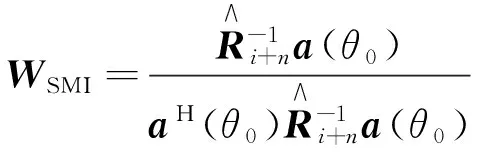
(14)

计算机仿真SMI算法方向图如图3所示。算法采用直线阵,天线阵元为18,实现了主瓣指向20°,在40°和60°产生零陷。设M为自适应横向滤波器的抽头数目,SMI算法在一次迭代中需要M3+M2次乘法和3次除法,计算复杂度记为O2(M)。SMI算法收敛速度较快,数值特征稳定，抗干扰效果较好。但是，计算复杂度较高,当采样较少时,引起波束图主瓣畸变、副瓣过高[11]。

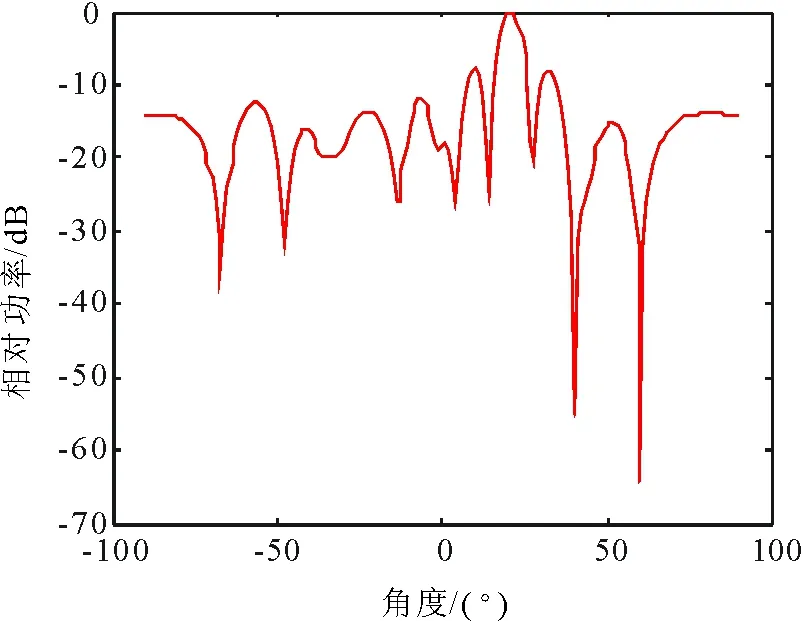
图3 SMI算法方向图Fig.3 Array beam patterns of SMI

2 WL-SMILMS算法

阵列接收信号具有多分辨率特性,这是使用小波理论的依据。预变换信号至多尺度小波域,降低信号的自相关性,可有效改善LMS算法收敛速度慢的缺点。针对不同频域采用不同算法,可相对降低计算复杂度。天线阵列信号难免受高斯白噪声污染，而小波域比时域更易去除这种噪声污染。基于此，文中提出基于小波变换的智能天线波束形成算法(WL-SMILMS)。

2.1 算法结构框图

基于小波的智能天线波束形成算法(WL-SMILMS),其系统由天线阵、小波分解、频率判断、LMS更新低频权矢量、SMI更新高频权矢量、权矢量融合、波束形成这些模块构成，结构如图4所示。

图4 WL-SMILMS算法结构框图Fig.4 Diagram of the WL-SMILMS algorithm structure

2.2 算法步骤

先用天线阵模块接收来波信号,包括期望信号、干扰信号1和干扰信号2。将含有干扰的数字天线阵信号通过db5小波分解到多尺度频域,得到信号的近似部分a3,细节部分d1,d2,d3,如图5所示。然后将信号a3，d1,d2,d3通过由FIR低通滤波器和减法器构成的频率判断模块,得到低频信号和高频信号。在采样率一致的情况下,一个周期内低频信号采样点较多,高频信号采样点较少,因此，针对高频信号采用采样矩阵求逆法进行权矢量更新,针对低频信号采用最小均方误差法进行权矢量更新。最后通过加法器实现各部分信号对应的权矢量求和,用融合后的权矢量更新滤波器抽头权值,实现最终的数字波束形成。

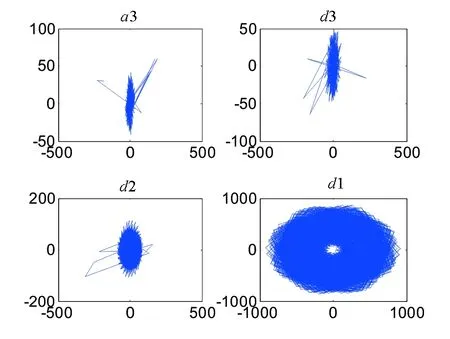
图5 小波分解图形Fig.5 Illustration of wavelet transform

2.3 计算复杂度分析

根据a3,d1,d2,d3能量大致分布,可得WL-SMILMS算法在一次迭代中的计算复杂度约为10%*O1(M)+90%*O2(M), 记为O3(M)。3

种算法的计算复杂度比较如表2所示。表2数据显示,WL-SMILMS算法的计算复杂度O3(M)明显低于SMI算法的复杂度O2(M),约为O2(M)的91%,降低了SMI算法9%的计算复杂度。

表2 LMS，SMI，WL-SMILMS算法的计算复杂度

Tab.2 Computational complexity of LMS, SMI, WL-SMILMS

算法计算复杂度LMS2M+1次乘法,2M次加法,记为O1(M)SMIM3+M2次乘法,3次除法,记为O2(M)WL-SMILMS10%×O1(M)+90%×O2(M),记为O3(M)

2.4 运行时间分析

LMS算法和WL-SMILMS算法在Matlab中运行时间如表3所示。由表3可看出,在相同阵元数目M下,WL-SMILMS算法较LMS算法运行时间短,运行时间提高了16.3%,使得波束形成收敛较快。

表3 LMS，WL-SMILMS运行时间

2.5 方向图分析

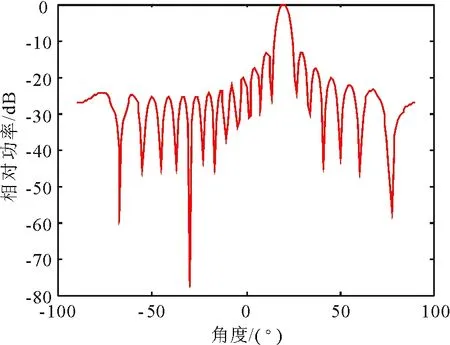
图6 WL-SMILMS算法方向图Fig.6 Array beam patterns of WL-SMILMS

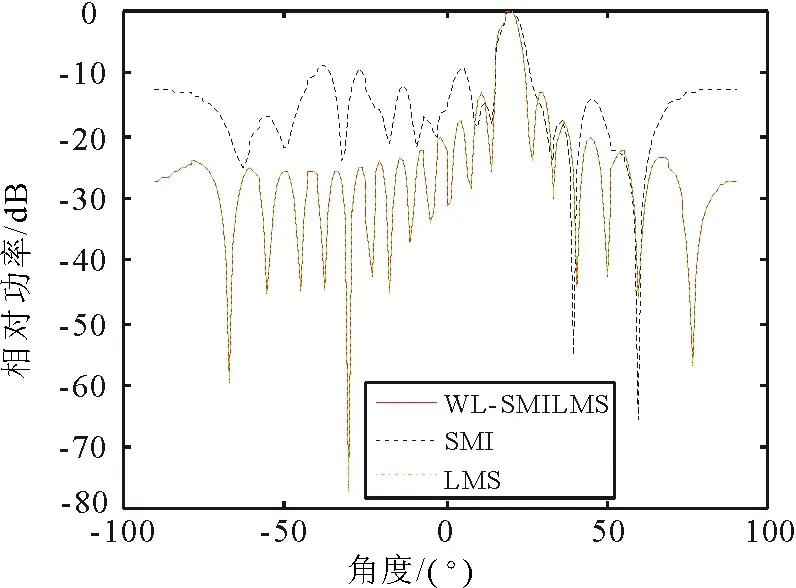
图7 LMS，SMI，WL-SMILMS算法对比图Fig.7 Three algorithms Comparison

计算机仿真WL-SMILMS算法方向图如图6所示。算法采用直线阵,天线阵元为18,实现了主瓣指向20°,在40°和60°产生零陷。相同条件下,LMS，SMI，WL-SMILMS算法对比图如图7所示。可见,WL-SMILMS算法克服SMI算法副瓣较高的缺点,旁瓣幅度平均降低10dB,约降低总幅度的15.2%。副瓣降低,提高了系统获取期望信号的准确性以及对干扰信号的抑制力。

3 结 语

基于小波变换的智能天线波束形成算法克服了采样矩阵求逆算法(SMI)复杂度高、副瓣较高的缺点,降低SMI算法9%的计算复杂度,副瓣幅度平均降低10dB,约降低总幅度的15.2%,同时克服最小均方误差算法(LMS)收敛慢的缺点,运行时间比LMS算法提高了16.3%。该算法实现了收敛率和计算复杂度的高度兼顾,满足复杂性电磁环境中精确获取目标的使用需求。

[1] LITVA J, LO T K.Digital beamforming in wireless communications[M].London:Artech House Publishers, 1996.

[2] GODARA L C.Application of antenna arrays to mobile communications. II.Beam-forming and direction-of-arrival considerations[J].Proceedings of the IEEE,1997,85(8):1195-1200.

[3] WINTERS J H. Smart antennas for wireless systems[J].IEEE Personal Communications Magazine,1998,5(1):23-27.

[4] GODARA L C. Application of antenna arrays to mobile communications. I:Performance improvements,feasibility,and system considerations[J].Proceedings of the IEEE,1997,85(7): 1031-1035.

[5] LIBERTI J C, RAPPAPORT T S.Smart antennas for wireless communications:IS-95 and third generation CDMA applications[M].Upper Saddle River, New Jersey:Prentice Hall PTR,1999.

[6] 赵永波,刘茂仓,张守宏. 一种改进的基于特征空间自适应波束形成算法[J].电子学报,2000,28(6):16-18.

[7] PADGETT J E, GUNTHER C G, HATTORI T.Overview of wireless personal communications[J].IEEE Communications Magazine.1995,33(1):28-41.

[8] RONG Z. Simulation of adaptive array algorithms for CDMA systems[D].United States: The Virginia Polytechnic Institute and State University,1996.

[9] LEE J C,UN C. Performance of transform-domain LMS adpative digital filters[J].IEEE Transactions on Acoustics, Speech, and Signal Processing,1986, 34(2):499-510.

[10] 李洪涛,贺亚鹏,朱晓华,等. 一种低快拍情况下稳健的波束形成算法[J].信号处理, 2011,27(6):808-812.

[11] WIDROW B, MANTEY P E, GRIFFITHS L, et al. Adaptive antenna systems[J].The Journal of the Acoustical Society of America, 1967, 42(5): 1175-1176.

[12] KUMARESAN R, TUFTS D W. Estimating the angles of arrival of multiple plane Waves[J].IEEE Transaction on Aerospace and Electronic Systems,1983,19(1):134-139.

(编 辑 李 静)

A smart antennas beamforming algorithm based on wavelet transform

LI Na1,2, YIN Xinghui2, GAO Wenyun2

(1.College of Mechanical & Electronic Engineering, Suzhou University, Suzhou 234000, China；2.College of Computer & Information, Hohai University, Nanjing 211100, China)

A smart antenna beamforming algorithm (WL-SMILMS) based on wavelet transform is proposed in this thesis. Received signals are transformed into multi-scale frequency domain by wavelet function. After the judgment of frequency, weight vectors of the high-frequency part and low-frequency part are respectively updated by sample matrix inversion (SMI) algorithm and least mean square (LMS) algorithm. Tap weights of filters are updated by the weight vector fusion from two parts for digital beamforming. Taking into account convergence rate and computational complexity, WL-SMILMS improves the complex calculation and high sidelobes of SMI algorithm, upgrades the convergence rate of LMS algorithm.

digital beamforming; wavelet transform; smart antennas; SMI; LMS

2015-07-07

国家自然科学基金资助项目(11173010,U1531101)

李娜，女，安徽宿州人，博士生，从事射频与通信系统研究。

TN911.72

A

10.16152/j.cnki.xdxbzr.2016-05-008