大兆瓦风电制动器闸片静动态多目标结构拓扑优化设计

沙智华,尹 剑,张生芳,刘 宇,马付建

(大连交通大学 机械工程学院,辽宁 大连 116028)



大兆瓦风电制动器闸片静动态多目标结构拓扑优化设计

沙智华,尹 剑,张生芳,刘 宇,马付建

(大连交通大学 机械工程学院,辽宁 大连 116028)

针对目前大兆瓦风电制动器制动过程中的振动与尖叫以及制动闸片在制动力作用下变形产生的磨损不均匀,根据实体各向同性材料惩罚函数的拓扑优化方法,采用折衷优化法定义多目标结构拓扑优化目标函数,在对制动闸片结构设计的同时,提高其静态刚度与动态振动频率,避免了单目标结构优化对问题考虑不周全的缺点,得到最佳拓扑模型.重构闸片模型,比对分析原模型与重构模型,结果表明:优化后的模型满足原模型静刚度且提高振动频率,同时避开尖叫频率,提高摩擦材料的利用率.

大兆瓦风电制动器; 制动闸片; 多目标拓扑优化; 折衷规划

在大兆瓦风力发电机组的安全保护装置中,制动器是保证无人值守风电机组长期安全运行的终端执行结构[1].风电制动器制动时,通过压缩弹簧推动制动推杆给制动闸片施加压力,推动制动闸片与制动盘接触,利用非旋转元件与旋转元件之间的相互摩擦来阻止转动或转动的趋势,最终实现停机.这一过程中,制动闸片为非绝对刚体,施加在其上的压力会使制动闸片自身发生翘曲变形,这会减小制动闸片与制动盘的接触面积,造成制动闸片磨损不均匀,降低摩擦材料的利用率.制动过程中往往伴随着振动与尖叫(高频振动),也会使制动效能有所下降.因此,如能通过结构改进使制动闸片的静态刚度与动态频率都能更好的满足制动过程需求,将对提高大兆瓦风电制动器制动效能、改善制动闸片损耗形式、提高摩擦材料利用率起到积极的作用.本文以制动闸片静态柔度最小化和动态特征值最大化为目标,采用实体各向同性材料惩罚函数的拓扑优化方法[2],对制动闸片的结构进行了多目标拓扑优化.

1 制动闸片工况分析及建模

风电制动器制动时,压缩弹簧推动制动推杆在制动闸片的上表面施加正压力,作用在中心圆形区域上,如图1所示.制动闸片与制动盘的接触会在制动闸片底面产生摩擦阻力.两侧凹槽沿着制动钳上的导轨运动,需要限制其接触面在x与y方向的移动自由度.制动闸片底面与制动盘接触,则需限制底面z方向的移动自由度.

对制动闸片进行模型简化后,划分有限元网格.制动闸片材料为铜基粉末冶金材料.其材料属性见表1[3].

模型上表面圆形区域施加正压力,下表面根据库伦摩擦定律施加相应的摩擦力.模型建立[4]后如图1所示.

表1 铜基粉末冶金材料属性

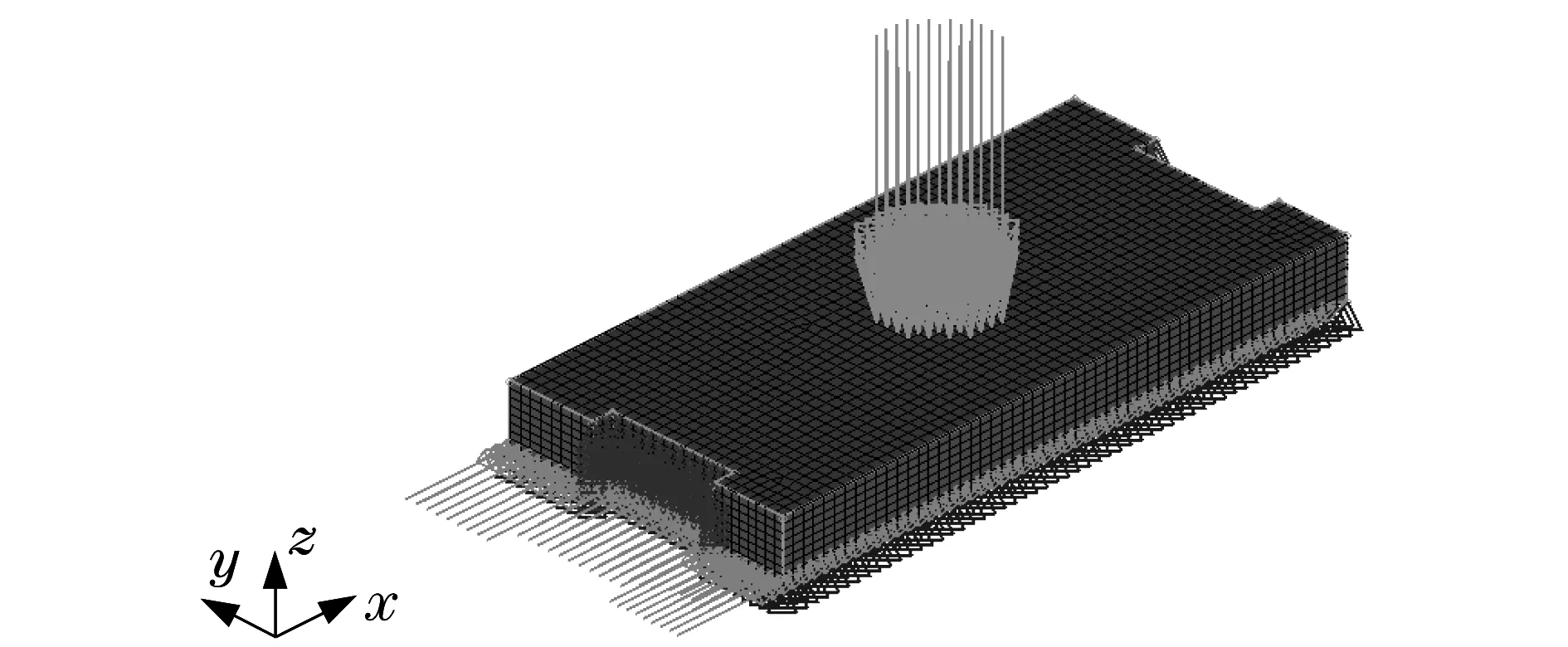
图1 风电制动器制动闸片模型Fig.1 Model of wind turbine brake pad

2 风电制动器制动过程分析

检测风电制动器制动过程中的力矩进行信号分析,得到如图2所示的制动曲线.在该工况下,制动曲线在19.16 s完成制动,制动力矩最大值为10 000 N·m.利用MATLAB软件中的快速傅立叶变换(FFT),对制动曲线进行时域到频域的变换,变换后的曲线如图3所示,其最大振动频率虽为17.66 Hz,但其振动的主要频率都分布在400 Hz以下.

制动过程中除振动外,还伴随着一定频率的尖叫.风电制动器在制动过程中产生的尖叫频率大约为2 100 Hz[5].因此,在对制动闸片的各阶频率进行优化时,需要同时避开振动的低频段与尖叫的高频段.

图2 风电制动器制动过程Fig.2 Braking process of wind turbine brake

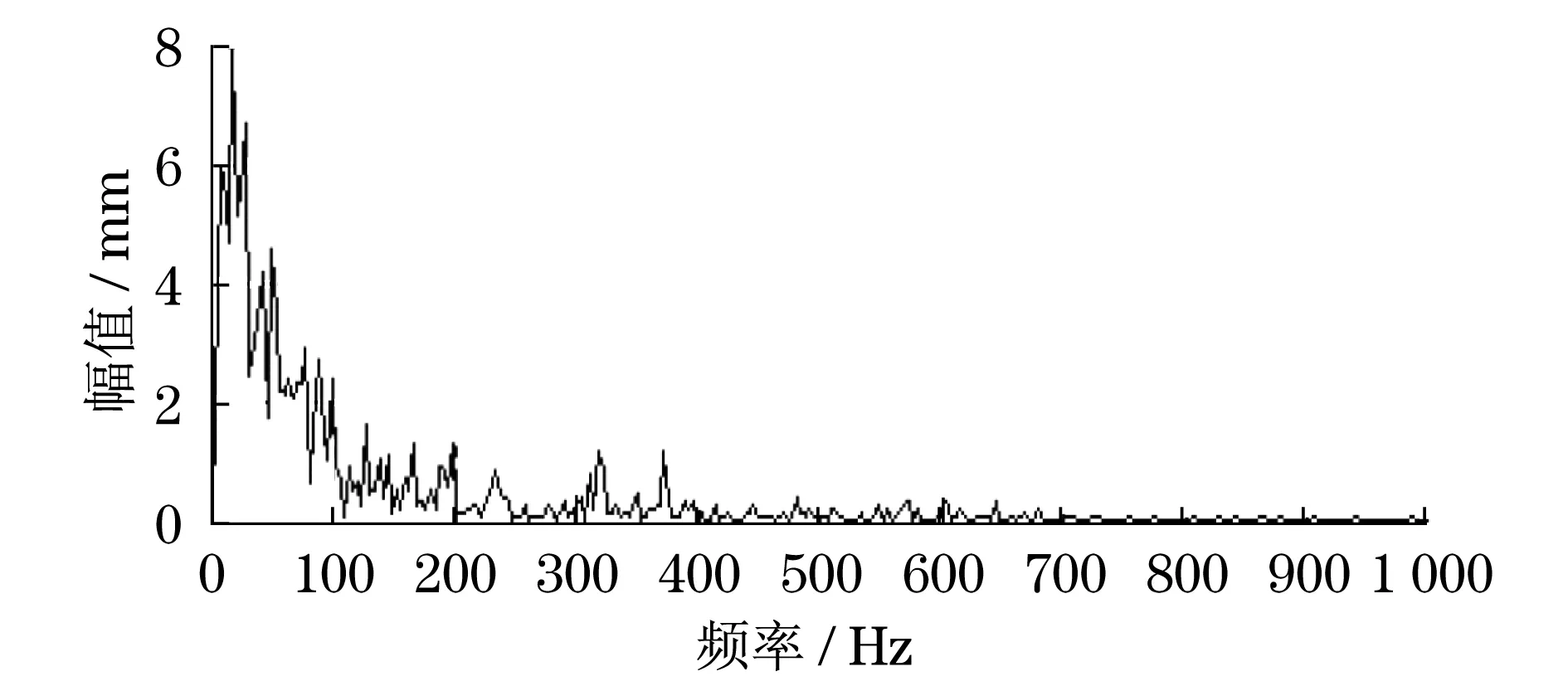
图3 制动过程中主要频率Fig.3 Main frequency in braking process

3 风电制动器制动闸片模态分析

考虑振动问题的研究过程主要侧重低阶模态,在约束条件下对制动闸片进行模态分析,提取其前4阶分析结果如图4所示.前4阶的制动闸片模态频率分别为796.17 Hz,1 629.39 Hz,1 872.54 Hz,2 684.55 Hz.制动闸片的第1阶振型是以xOy平面内沿y轴的弯曲为主,第2阶振型是以xOy平面内沿x轴的弯曲为主,第3阶振型是以xOy平面内沿y轴的扭曲为主,第4阶振型是以xOy平面内沿x轴的扭曲为主.从分析结果可以看出,制动闸片的第1阶模态频率已经大于制动过程中的振动频率,因此需要对高阶模态频率进行优化.

4 多目标结构拓扑优化

4.1 多目标结构拓扑优化目标函数

采用实体各向同性惩罚微结构模型将有限元模型设计空间每个单元的密度ρ设为设计变量,它与结构的材料参数有关,满足:

图4 风电制动器制动闸片有限元模态分析结果Fig.4 Results of FEM modal analysis on wind turbine brake pad

(1)

式中:E为弹性模量;p为惩罚因子,p>1;ρmin为材料每个单元的最小密度值;ρ为每个单元的材料密度[6].

多目标结构拓扑优化是以体积作为约束,同时考虑静态刚度目标和动态振动频率目标的拓扑优化.因此采用折衷规划法,其目标函数可定义为:

(2)

式中:H(ρ)为多目标结构优化目标函数;C(ρ)为静态刚度目标函数;Cmin和Cmax为静态刚度目标函数的最小值与最大值;F(ρ)为动态振动频率目标函数;Fmin和Fmax为静态刚度目标函数的最小值与最大值;ω1为静态刚度目标函数的权重系数;ω2为动态振动频率目标函数的权重系数,满足ω1+ω2=1.

为了使优化结果更理想,需要对优化进行一定约束.为使寻找最优解的范围适当减小,限制优化后模型的体积百分数最少为50%,同时,为使制动闸片不被压溃,限制受正压力处的位移在±0.05 mm范围内.

4.2 多目标结构拓扑优化分析

设置拓扑优化分析中的响应分别为静态刚度响应和动态频率响应,并分别设置优化目标函数为静态刚度最大化、静态刚度最小化、动态频率响应最大化和动态频率响应最小化,进行优化分析后,可得:

(3)

取ω1=0.7,则动态振动频率目标函数的权重系数ω2=0.3.设置多目标结构拓扑优化中的响应静态刚度响应、动态频率响应、体积百分数响应以及约束节点的位移响应.设置体积百分数响应和约束节点位移响应为约束条件,并使用自定义函数将静态刚度响应和动态频率响应设置为目标函数,进行多目标结构拓扑优化.最终在设计可行域中寻求使H(ρ)最小的最优解.

5 拓扑优化结果及其分析

利用工程上常用的拓扑优化软件OptiStruct,在上述约束条件下,优化出制动闸片结构，如图5所示.优化后的制动闸片前4阶模态频率分别为660.92,1384.37,1397.15,3214.15 Hz.

图5 多目标结构拓扑优化结果Fig.5 Result of multi-object structure topology optimization

图6 重构的制动闸片结构Fig.6 Reconstructed structure of brake pad

因此,根据拓扑优化结果设计的闸片结构能够满足大兆瓦风电制动器高能效制动闸片的结构设计的要求.就其前4阶模态频率而言,各阶模态均超过制动过程振动频率分布的400 Hz,而且第2,3,4阶模态频率相对于尖叫频率2100 Hz都有较大幅度的远离.这对制动过程中的振动和尖叫有一定程度的抑制作用.图5a显示的材料密度区间为[0,1],而图5b显示的密度区间为[0.4,1].图5b与图5a比较,沿y轴两侧的网格密度为0.这是由于闸片在制动过程中受到制动推杆的推力,与制动盘接触过程中产生了翘曲变形,使得两侧材料磨损不均匀造成的.图5b中,摩擦力的方向沿x轴正向,制动闸片右侧的部分承受着推杆正压力与摩擦力的合力,因此闸片右侧略宽于左侧.在制动闸片两侧开不同大小的空洞,也是提高各阶模态频率方法.

图7 优化后设计的制动闸片静力刚度分析Fig.7 Static stiffness analysis of optimized brake pad

基于拓扑最佳模型重构制动闸片结构,得到如图6所示的模型.对新设计出的制动闸片结构进行静力刚度检验,得到位移和应力云图如图7所示.

对新设计出的制动闸片结构进行模态分析,得到其前4阶模态频率分别为473.71,1 010.55,1 169.96,3 059.97 Hz.新结构在体积和质量上比原结构减小39.1%,新结构提高了铜基粉末冶金摩擦材料的利用率,降低了闸片的更换频率.前4阶频率均有所提高,其中第4阶模态频率较之前提高了14.0%.

6 结语

本文针对目前大兆瓦风电制动器制动过程中的振动与尖叫以及制动闸片在制动力作用下变形产生的磨损不均匀,利用快速傅里叶变换对制动曲线进行时域谱到频域谱的转换,进而得到容易产生振动的频率范围,采用实体各向同性材料惩罚函数的拓扑优化方法,在满足工作要求的前提下,以制动闸片的静态柔度最小化和动态特征值最大化为优化目标,设计了制动闸片的新结构.新结构在体积和质量上比原结构减小39.1%,提高了铜基粉末冶金摩擦材料的利用率,降低了闸片的更换频率.优化过程中考虑避开制动过程中的振动频率及尖叫频率,使制动闸片的第4阶模态频率较之前提高了14.0%.对优化结构进行计算机仿真检验,仿真结果表明,新结构的静态刚度与动态频率满足实际要求.

[1] 熊维军,晏红文.兆瓦级风电机组机械制动扭矩的计算方法和制动器选型计算[J].机械制造与自动化,2011(5):137-138.

XIONG Weijun,YAN Hongwen.Calculation of mechanical brake torque for mw level wind generating unit[J].Machine Building & Automation,2011(5):137-138.

[2] QING Li,STEVEN G P,QUERIN O M,et al.Shape and topology design for heat conduction by Evolutionary Structural Optimization[J].International Journal of Heat and Mass Transfer,1999,42:3361-3371.

[3] 于潇,郭志猛,郝俊杰,等.风电用铜基粉末冶金制动闸片的制备与性能[J].粉末冶金材料科学与工程,2014,19(1):66-70.

YU Xiao,GUO Zhimeng,HAO Junjie,et al.Preparation and properties of copper-based powder metallurgy brake pad for wind turbine[J].Materials Science and Engineering of Powder Metallurgy.2014.19(1):66-70.

[4] 刘宇,张生芳,宋雪萍,等.动力平板车车架结构的拓扑优化设计[J].中国工程机械学报,2014,12(2):34-37.

LIU Yu,ZHANG Shengfang,SONG Xueping,et al.Topological optimization design on frame structure of power platform trailers[J].Chinese Journal of Construction Machinery,2014,12(2):34-37.

[5] 赵兴华.风电制动器钳体振动稳定性分析与设计[D].大连:大连理工大学,2009.

ZHAO Xinghua.Design and vibration stabilization analysis of the caliper construction in wind-driven generator[D].Dalian University of Technology,2009.

[6] 范文杰,范子杰,苏瑞意.汽车车架结构多目标拓扑优化方法研究[J].中国机械工程,2008(12):1505-1508.

FAN Wenjie,FAN Zijie,SU Ruiyi.Research on multi-objective topology optimization on bus chassis frame[J].China Mechanical Engineering,2008(12):1505-1508.

Topological optimization design on stati-dynamic multi-object lstructure for arge-megawatt wind turbine brake pads

SHA Zhi-hua,YIN Jian,ZHANG Sheng-fang,LIU Yu,MA Fu-jian

(School of Mechanical Engineering,Dalian Jiao Tong University,Dalian China 116028)

To avoid the vibration, screaming and uneven wear from brake pad deformation, the braking force in a large-megawatt wind turbine brake is investigated. According to the topological optimization method for solid isotropic material with penalization, a multi-object structure topology optimization function is defined via compromise programming to design a new structure on brake pad to improve both static rigidity and dynamic vibration frequency. As such, the disadvantages from single-object structure optimization are avoided by multi-object structure optimization for optimal topology model.In addition, this proposed model is reconstructed in comparison with the original model. Therein, it is indicated that the reconstructed model meets the static and dynamic requirements.Meanwhile, this approach avoids the screaming frequency and improves the frictional material utilization rate.

large-megawatt wind turbine brake; brake pad; multi-object topological optimization; compromise programming

国家自然基金资助项目(51475066)；大连市科学技术基金资助项目(2013J21DW011)

沙智华(1973-),女,教授.E-mail:zhsha@djtu.edu.cn

TH 122

A

1672-5581(2016)04-0332-05