多自由度内共振系统的非线性动力学行为分析

李小彭,安镰锤,李加胜

(东北大学机械工程与自动化学院,辽宁 沈阳 110819)



多自由度内共振系统的非线性动力学行为分析

李小彭,安镰锤,李加胜

(东北大学机械工程与自动化学院,辽宁 沈阳 110819)

为了深入研究多自由度内共振系统的非线性动力学行为,通过对切削过程中切削力变化状况的分析,建立了包含工件-刀架子系统的多自由度非线性系统的切削颤振模型以及系统的振动方程.基于Poincare映射和分岔理论,得到了系统随进给速度变化时的全局分岔图以及系统在速度变化过程中的运动状态和系统振幅的变化情况.MATLAB软件在1:2内共振时的数值仿真结果表明:在1:2内共振时,工件子系统运动状态主要为准周期运动和混沌运动,而刀具子系统运动状态主要为准周期运动.通过切削颤振的分析结果可知,当系统发生1:2内共振时,工件-刀具子系统除了产生自激振动外,还出现了比较复杂的单自由度自激振动系统中没有出现的多环运动和混沌运动,表明多自由度或弹性体系统会出现单自由度预测和解释不了的现象.

内共振; 非线性动力学; 切削颤振; 分岔; 自激振动

颤振是金属切削过程中刀具与工件之间产生的一种强烈振动,它不仅降低了工件的加工质量，还会影响刀具和车床的使用寿命,而且还产生切削噪声.关于机床的颤振的研究,国内外学者一般都是始于颤振机理与模型的研究.而切削颤振机理与模型的研究基本都集中在再生型颤振[1-3].ARNOLD第一次提出了摩擦型颤振机理.后来一些学者通过建立刀架或工件的单自由度模型或单弹性体模型进行了颤振机理研究[4].陈花玲等在迟滞非线性理论基础上建立了新的颤振理论模型,并且运用等效线性法得到了模型的稳定阈的近似解以及符合实际的三维稳定性图,解释了颤振振幅稳定性、微幅倾振以及双频旅振等现象[5].GDANIEC等通过采用LuGre摩擦模型来进行单自由度的摩擦振子的研究,发现对于不同的进给速度和摩擦系数会产生摩擦诱发振动中的分岔和混沌现象,而且大部分的运动都为混沌运动[6].MADELEINE研究了一个两自由度的质量-阻尼-弹簧系统在受到间歇加载时的摩擦激振现象[7].刘习军等建立了在非线性动态切削力耦合下的由刀架及工件弹性子系统构成的多自由度理论模型,解释了系统内共振的机理,开拓了速度型颤振研究的一个新思路[8].另外,由于受到模型的限制,许多颤振现象无法进行很好的解释[9].因此,本文建立了刀架子系统与工件子系统构成的多自由度数学模型,然后得到了整个系统的动力学方程,并通过数值计算分析得到了“刀具和工件子系统在1:2内共振时自激振动主要为纯滑动和混沌运动”这样一个结论，该结论在一定的程度上解释了金属切削时摩擦引起颤振的一些现象.

1 切削颤振系统动力学模型的建立

在机床切削过程中,车刀相对工件在切削表面相对滑动,在一定条件下,刀具与工件之间的动态切削力将使车刀或工件产生颤振[10].设机床床身的刚度足够大,则可以将刀具、支架及工件、夹具分别看成为两个弹性子系统,如图1所示.

图1 工件及刀具系统示意图

设w1，w2分别表示刀具的横向位移函数和工件的纵向位移函数;ρ为刀具单位体积质量;E为弹性模量；I为横截面对中心主轴的惯性矩；A为横截面积.结合动力学理论得到刀具子系统和工件子系统的动力学方程:

(1)

(2)

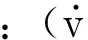
本文采用Stribeck摩擦模型,摩擦系数与相对速度的非线性关系如下:

(3)

式中：μs,μm分别静、动摩擦系数；vm为对应于最小摩擦的速度.

由模态正交性理论,设方程(1)和(2)的解可表示为模态的线性组合:

(4)

式中：H1i(x)，H2j(y)分别为工件、刀具弹性子系统的振型函数；X1i(t)，X2j(t)分别为工件、刀具弹性子系统振动函数的广义坐标;i,j为模态阶段.

运用振型函数和模态阵型的正交性,得到动态切削力作用的工件、刀具子系统构成的多自由度自激振动方程:

(5)

式中：ω1j，ω2j分别为工件、刀具的固有频率；p1i(t)，p2j(t)为非线性模态广义力函数.

对方程(5)进行无量纲化,得到此系统无量纲化的非线性振动方程为

(6)

式中：H1,H2分别为工件、刀具弹性子系统一阶的振型函数；X1,X2分别为工件、刀具弹性子系统位移；N为平均力；a1,b1,c1为试验拟合参数.

2 内共振系统的动力学分析

摩擦自激振动系统中存在内共振关系的振动非常普遍.摩擦系统的内共振振动会使振动表现出区别于一般单自由度非线性系统振动中的动力学行为.因此,本文研究系统可能发生的1:2 内共振行为.

2.1 1:2内共振系统仿真分析

假定参数如下:k1=1,k2=2,工件的广义横坐标X11=0.6m,刀具的广义横坐标X22=0.53m,N=10N,a=0.3,b=0.1,c=0.1,H1=H2=1.

现在利用Runge-Kutta法对整个系统方程进行数值模拟,得到的工件及刀架的位移随进给速度的分岔图,还有其相图、时域曲线图及Poincare截面图如图2，3所示.

图2 以进给速度为参数的系统分岔图

Fig.2 Bifurcation diagram of the system with the feed speed as the bifurcation parameter

图3 v0=0.1 m·s-1时切削系统的时域图、相图和Poincare截面图

图4 v0=0.2 m·s-1时切削系统的时域图、相图和Poincare截面图

图5 v0=0.4 m·s-1时切削系统的时域图、相图和Poincare截面图

由这些特征曲线图可以看出,系统运动可分为以下阶段:

(1) 当进给速度v0>vc1时,工件子系统将稳定在平衡点,此时相对速度即带速度.

(2) 当进给速度满足v0≤vc1时,工件子系统的平衡点发生失稳,系统产生自激振动.并且这个过程又可以分成3个阶段.开始阶段即当进给速度v0

图6 v0=0.54 m·s-1时切削系统的时域图及相图

图7 v0=0.7 m·s-1时切削系统的时域图及相应相图

由分岔图可以看出,进一步分析带速度减小过程中运动的变化.在l:2内共振情况下,工件子系统运动状态主要为周期和混沌运动.实际上,系统平衡点失稳后的纯滑动已经是多环运动,其后进入更复杂的黏-滑自激运动.而刀具子系统的运动状态主要为周期运动.

3 小结

(1) 通过对切削过程中切削力的变化状况进行分析,建立了包含工件子系统和刀架子系统的多自由度非线性系统的切削颤振模型; 然后建立系统的振动方程.最后,基于Poincare映射和分岔理论,得到了系统随进给速度变化时的全局分岔图,得到了系统在速度变化过程中的运动状态,并获得了系统振幅的变化情况.

(2) 运用MATLAB软件得到了机械系统在1:2内共振时的数值仿真结果.在1:2内共振时,工件子系统运动状态主要为准周期和混沌运动,而刀具子系统运动状态主要为准周期运动.通过切削颤振的结果可以发现,当系统发生1:2内共振时,工件和刀具子系统除了产生自激振动以外,还出现了比较复杂的单自由度自激振动系统中没有出现的多环运动和混沌运动,表明多自由度或者弹性体系统还是会出现单自由度预测和解释不了的现象.

[1] 师汉民.影响机床颤振的几个非线性因素及其数学模型[J].华中工学院学报,1984,12(6):101-112.

SHI Hanmin.Several nonlinear factors affecting chatter of machine tool and its mathematical model[J].Journal of Huazhong University of Science and Technology,1984,12(6):101-112.

[2] 吴雅.金属切削机床切削噪声的动力学研究[J].机械工程学报,1995,31(5):76-85.

WU Ya.Dynamic study on cutting noise of metal cutting machine tool[J].Journal of Mechanical Engineering,1995,31(5):76-85.

[3] 罗作国.切削颤振辨识及主动抑制策略的研究[D].武汉:华中科技大学,2007.

LUO Zuoguo.A Thesis submitted in partial of fulfillment of the requirements[D].Wuhan:Huazhong University of Science and Technology,2007.

[4] HANNA N H,TOBIAS S A.The nonlinear dynamic behaviors of a machine tool structure[J],Int.Journal of MT-DR,1969,9:193-207.

[5] 陈花玲.机床切削颤振的非线性理论研究[J].振动工程学报,1992,5(4):335-342.

CHEN Hualing.Nonlinear theoretical study on cutting chatter of machine tools[J].Journal of Vibration Engineering,1992,5(4):335-342.

[6] GDANIEC P,WEIβC,HOFFMANN N P.On chaotic friction induced vibration due to rate dependent friction[J].Mechanics Research Communications,2010,37:92-95.

[7] MADELEINE P.New limit cycles of dry friction oscillators under harmonic load[J].Nonlinear Dynamic,2012,70:1435-1443.

[8] 刘习军.机床速度型切削颤振的非线性研究[J].振动与冲击,1999,18(2):5-9.

LIU Xijun.Nonlinear research on speed cutting chatter of machine tools[J].Journal of Vibration and Shock,1999,18(2):5-9.

[9] SHI Hanmin,TODIAS S A.Theory of finite amplitude machine tool instability[J].Journal of Machine Tool Design and Research,1984,24(1):45-69.

[10] 刘习军,王立刚,贾启芬.一种由干摩擦引起的车床切削颤振[J].工程力学,2005,22(1):107-122.

LIU Xijun,WANG Ligang,JIA Qifen.Cutting chatter of machine tools induced by dry fraction[J].Engineering Mechanics,2005,22(1):107-122.

Analysis on nonlinear dynamical behaviors via multi-DOF internal resonance system

LI Xiao-peng,AN Lian-chui,LI Jia-sheng

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

To further study the analysis on nonlinear dynamical behaviors via multi-DOF internal resonance system, the cutting force variation is first analyzed.Then, the multi-DOF nonlinear system model for cutting chatter, which comprises the artifacts-rest subsystem and system vibration equation, is then established.Based on the Poincare maps and bifurcation theory, the global bifurcation diagram is obtained with changes of feed speed, motion state and amplitude.Finally, it is found from numerical simulation via MATLABTM regarding 1/2 internal resonance that the motion states of workpiece subsystem are mainly the quasi-periodic and chaotic motions, whereas the cutting tool subsystem motions are mainly the periodic motions.By analyzing the cutting chatters, the workpiece-tool subsystem produces the self-excited vibration as well as more complex polycyclic and chaotic motions.Therefore, the self-excited vibration cannot be predicted by the single degree of freedom system but the multi-degree of freedom or elastomer system.

internal resonance; nonlinear dynamics; cutting chatter; bifurcation; self-excited vibration

国家自然科学基金资助项目(51275079); 辽宁省百千万人才工程培养经费资助(2014921018).

李小彭(1976-),男,教授,博士生导师.E-mail:xpli@me.neu.edu.cn

U 463.51

A

1672-5581(2016)03-0187-06