滑行车运行过程的动力学仿真

朱玉田,郑立辉,刘钊

(同济大学 机械与能源工程学院,上海 201804)



滑行车运行过程的动力学仿真

朱玉田,郑立辉,刘钊

(同济大学 机械与能源工程学院,上海 201804)

根据滑行车轨道形状,计算获得轨道的几何参数.基于轨道几何参数建立了考虑实际车长的滑行车动力学模型,通过Simulink动力学仿真,获得了滑行车上不同位置点运行过程中的行程、速度、加速度、车体姿态等的时间历程曲线,以及滑行车运动参数与轨道位置的关系曲线.同时计算获取了滑行车运行过程中人体的感受情况.通过与ADAMS仿真结果对比检验了此动力学模型的可信度,为轨道类车辆滑行车等的运动参数仿真提供了一种新思路.仿真结果和分析方法可为滑行车的设计、安全性评估等提供参考.

滑行车; 柔性体; 人体感受; Simulink

滑行车类游乐设施如过山车、滑行龙、疯狂老鼠等是各大游乐园必备的设施,通常由车辆和轨道组成,运行时车辆由驱动装置提升至一定高度,然后在重力的作用下沿轨道自由下滑,完成俯冲、急转、翻滚等动作.该类游乐设施速度高,运动形式富于变化,刺激性强,深受青少年的喜爱,其中过山车更素有“游艺机之王”的称号[1].如今,大型游乐设施正朝着更高、更快、采用更多的先进技术、运动形式更加复杂等方向发展.目前,全球最快的过山车最高速度可达205 km·h-1,最大提升高度可达139 m.然而,随着滑行车类游乐设施刺激性的增强,其危险性也在成倍增加,安全事故在世界各地都时有发生[2-4].高速运行游乐设备发生的事故非常严重,社会影响恶劣.因此,对滑行车的动力学设计和安全保障评价也提出了更高要求.近年来,人们基于虚拟样机技术,一般采用多体动力学仿真软件对滑行车的运动学及动力学仿真进行了广泛的研究,取得了一定的研究成果[5-9].如梁朝虎等[1]建立了滑行车的ADAMS仿真模型,仿真获取了滑行车运行时的速度、加速度等运动参数且仿真结果与实测数据比较接近.但此类方法针对轨道、车体等的建模需花费一定时间.

本文将过山车类滑行车作为研究对象,通过计算获得轨道几何参数,把滑行车简化为有限长柔性体并基于轨道几何参数建立其动力学方程,通过Simulink仿真计算,对滑行车运动特性进行了研究,此方法不需建立轨道、车体等三维模型且计算速度优于ADAMS仿真,为轨道类车辆滑行车的运动仿真提供了一种新思路.在本文研究的基础上,可以进一步对滑行车的振动特性进行研究.

1 轨道几何参数

滑行车由多节车厢连接而成,为了计算方便,假设滑行车为有限长的柔性体,长度L=15 m,以某游乐园的大型单环往复式滑行车为对象,其运行轨道采用弧坐标s表示，如图1所示.o点为弧坐标参考原点,图中箭头所指为弧坐标正方向.由于此滑行车轨道只有立环上端c,d,e段为空间轨道,其余各段均为平面轨道故此处将其近似为平面轨道.此轨道由15段直线和圆弧组成,轨道形状特征较简单的描述方法可用θ角来表示,θ角为轨道某点的法线与铅垂线方向的夹角,根据轨道形状可计算得到角度θ随轨道位置(弧坐标s即沿轨道距离原点的距离)变化的关系θ=θ(s),如图2a所示.

图1 某游乐园滑行车运行轨道Fig.1 Track of roller coaster in an amusement park

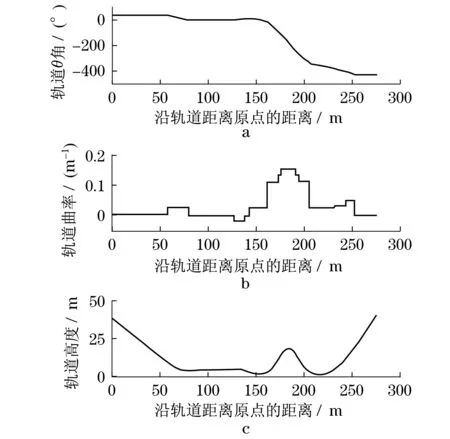
图2 轨道θ角、曲率、高度与位置的关系Fig.2 Relation between θ,curvity and height of the track and position

根据轨道的θ角,可进一步得到轨道任意位置处的曲率1/R,R为轨道的曲率半径,曲率随位置变化的关系1/R=1/R(s),如图2b,假定从滑行车向下看向轨道,凹弧的曲率为正.

同理,根据轨道的θ角,可进一步获得轨道高度与位置的关系y=y(s),如图2c所示.

2 滑行车的动力学仿真模型

2.1 滑行车仿真工况

主要研究车体的滑行工况,滑行车从o点开始在重力作用下按o-a-b-c-d-e-f-g的轨道运行,如图1所示(图1中b点在f点的前面),自由滑行至轨道尾端g点后,短暂静止,由于重力的作用,车体继续按g-f-e-d-c-b-a轨道反向滑行至停车位置a点处.

2.2 滑行车运行的动力学方程

设滑行车沿轨道的切向速度为v,在同一时刻滑行车上任意点的切向速度相同,由动能定理的微分形式[10],建立滑行车的动力学方程,

(1)

式中:m为滑行车质量,m=12 000 kg;δW为元功,即车体所受外力在无限小位移中所作的功,滑行车在运行过程中的受力包括,重力、阻力和轨道对车体的支撑力,因此δW=δWG+δWR+δWH,WG,WR,WH分别表示重力,阻力和支撑作的功,其中支撑力方向与滑行车运动方向垂直,故支撑力不做功,从而δW=δWG+δWR.设滑行车所处位置如图1所示,车尾高度为y1,经过dt时间滑行车以速度v运动到y2(车头高度),在dt时间内重力对滑行车作的功可等效为,微质量ρvdt从y1运动到y2所作的功,其中ρ=800 kg·m-1,为滑行车单位长度的质量,所以,

(2)

阻力与滑行车运动方向相反,故阻力作负功,即,

(3)

式中:fR为阻力.将(2),(3)式带入式(1)后,两边除以dt,得:

(4)

由ds=vdt,上式(4)两边消去v后可进一步化简为:

(5)

初始条件为s(0)=0,另外,式(5)中,fR=fFR+fDR,其中,fFR为摩擦阻力,表示为

(6)

式中:FN(s,l)为滑行车单位长度上的正压力,此处将滑行车平均分成6段,采用每段中点处法向加速度和重力加速度求出每段所受摩擦力,再将6段所受摩擦力相加近似计算出滑行车所受摩擦力,其中μ为轮轨摩阻系数,取0.03,an(s,Li/12)=v2(s)/R(s+Li/12).

(7)

式中,fDR为空气阻力,CD为空气阻力系数与车体形状有关,此处取值为0.6,A为滑行车的迎风面积,A=1.766 m2,ρa为空气密度,一般ρa=1.225 8 N·s2·m-4,vr为相对速度,在无风时即为滑行车的车速v,此处假设滑行车在无风条件下运行,即vr=v[11].

将式(6)和(7)代入式(5)得,

(8)

其中,Δy(s)为运行过程中滑行车的车尾与车头的高度差,即Δy(s)=y1(s)-y2(s)=y(s)-y(s+L).

3 滑行车动力学模型的仿真分析

3.1 Simulink模型及仿真结果

利用Matlab软件中的Simulink组件对式(8)进行仿真计算,搭建的Simulink模型如图3所示.模型中,利用Simulink库中的Matlab Function模块调用m文件以Matlab语言形式表述的θ(s)、Δy(s)函数等以实现对式(8)的求解,图3中的u表示Simulink模块的输入数据.

仿真计算获取的滑行车车尾点行程如图4a,从图中可以看到,运行时间为15.5 s时,车体运行至轨道右端最高点,之后开始反向滑行,车体反向滑行的行程为负值,当行程为105.1 m时,滑行车反向滑行至轨道的停车位置,仿真结束.在同一时刻滑行车上任意点的切向速度,切向加速度,大小相同,图4b为滑行车的行驶切向速度的时间历程,从图中可以看到,滑行车最大行驶速度为23.4 m·s-1,在运行时间为15.5 s时,滑行车的行驶速度降为0,表示此刻滑行车运行到轨道的尾端最高处,之后在重力作用下反向滑行,这时速度为负值.滑行车运行过程中车体的姿态角随轨道位置不断变化,下图5a为车尾点运行过程中的姿态角,此角度为车体在轨道上所在点的法线与铅垂线方向的夹角即图1中的θ角.滑行车的行驶切向加速度小于1 g,见图5b,行驶切向加速度方向与车体前进方向一致时为正.在圆弧轨道上的滑行车上不同位置点的法向加速度大小在同一时刻可能不同见图6,已知法向加速度方向沿轨道法线,指向轨道曲率中心,假定法向加速度由轨道指向乘客的方向为正,滑行车最大行驶法向加速度小于60 m·s-2,满足国标GB 8408-2008,游乐设施安全规范中规定的加速度允许值.

为了检验上述Simulink模型计算的可信度,同时在ADAMS中建立了滑行车的多体动力学模型,ADAMS三维模型包括轨道和滑行车车体,均根据实际物理样机尺寸建立,其中,车体主要由车厢、车架、转向架以及轮架组成,建模过程中忽略了部分对计算结果不带来较大误差的细节,如车轮与车轮轴之间的滚动轴承,轮架与转向架之间的连接螺栓等,轮轨摩擦系数以及空气阻力参数与式(6)和(7)中参数设置相同,ADAMS虚拟样机见图7.ADAMS仿真获取的滑行车行驶切向速度和行驶法向加速度与Simulink模型的计算结果对比如图8,从图中可以看到,Simulink计算和ADAMS仿真的两曲线形状基本相同,所以将滑行车近似为有限长柔性体模型计算其运动参数的方法可行,但二者幅值略有不同,这是由于Simulink模型将滑行车假设为柔性体以及轨道近似为平面轨道带来的误差.但Simulink模型较ADAMS仿真建模更便捷,计算速度快,尤其是Simulink模型中轨道采用弧坐标表示后再建立滑行车运动方程的方法较容易获取其运动参数随轨道位置变化的关系曲线,且此曲线对作为典型运动关联型设备的滑行车的设计、安全性评估等具有重要意义.滑行车运动参数与轨道位置的关系将在下一节中详细叙述.

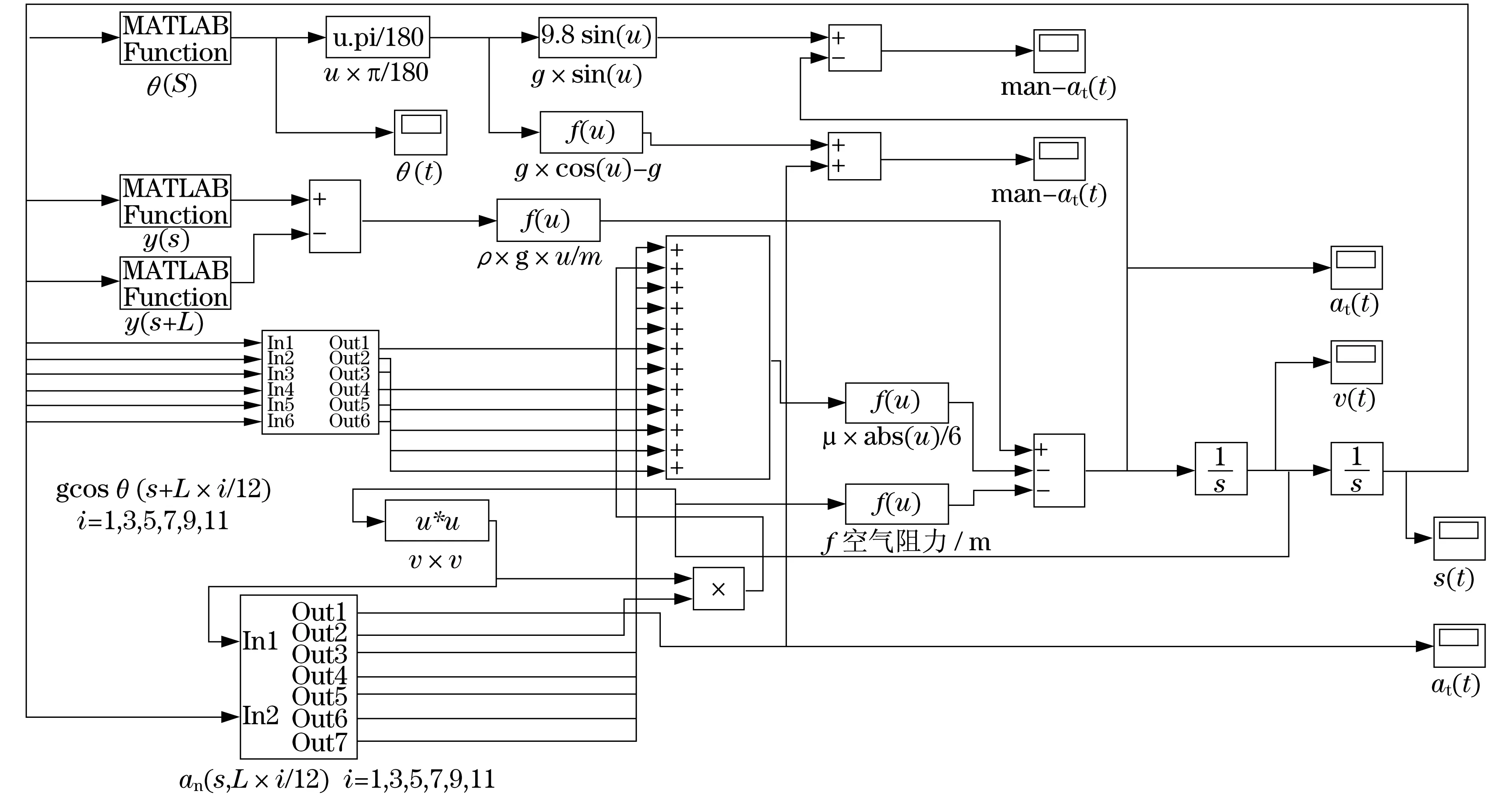
图3 滑行车运动仿真Simulink模型Fig.3 Simulation Simulink movement model of the roller coaster

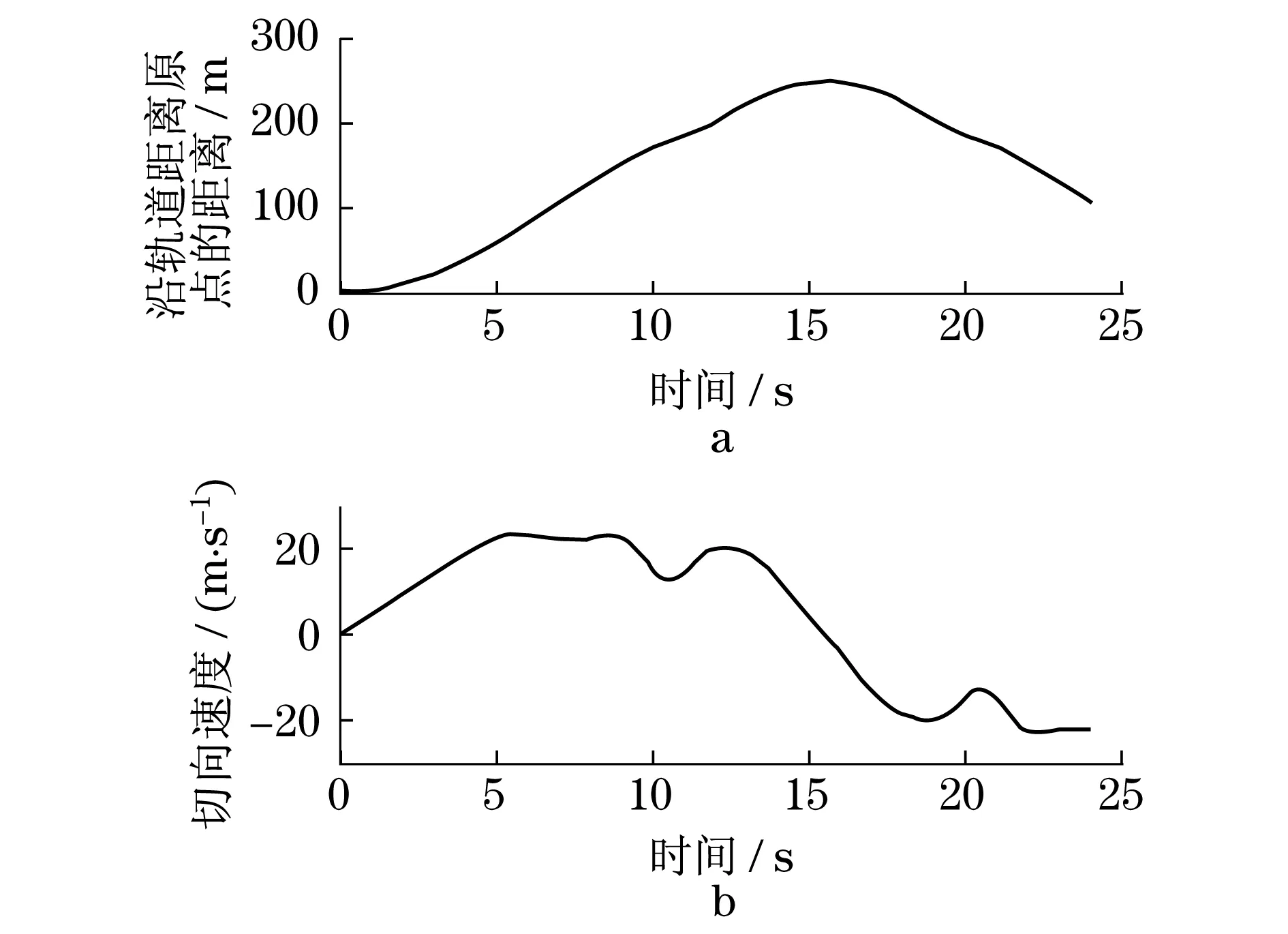
图4 滑行车车尾点行程、行驶切向速度Fig.4 Travel route of the rear point and tangential velocity of the vehicle

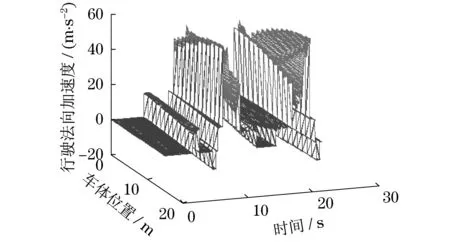
图6 滑行车不同位置点行驶法向加速度Fig.6 Vertical acceleration of different points on the roller coaster

3.2 运动参数随弧坐标s的变化关系

滑行车为典型的运动关联型设备[12],即滑行车车体的高频随机振动与其宏观运动如行驶速度、加速度等运动参数相互关联,如当滑行车的宏观运动随着载重、阻力等因素的变化而变化时,对应随机振动的振幅、频率等时频特性在时域内的分布随之变化.所以滑行车经过轨道某一位置处的运动参数如速度、加速度等,在滑行车的故障诊断与预警中尤其重要.根据滑行车行程以及其运动参数与时间的映射关系可以获得运动参数与行程的关系曲线.在轨道同一位置处,滑行车不同位置的通过速度可能不同,如下图9a为滑行车行驶切向速度与行程的关系,滑行车行驶至s=70.2 m处车尾首先到达最大车速23.4 m·s-1.图9b为滑行车行驶法向加速度与行程的关系,当滑行车运行至s=161.3 m处即滑行车在进入轨道的立环位置之前,车头处的法向加速度达到最大值.

图7 滑行车ADAMS仿真模型Fig.7 ADAMS model of roller coaster

图8 Simulink计算和ADAMS仿真运动参数比较Fig.8 Motion parameters comparison between Simulink and ADAMS model

根据滑行车运动参数与位置的关系,可以进一步获得滑行车运行至不同位置时的受力情况,以滑行车的车尾为例,根据图2a轨道θ角与位置的关系,滑行车运行至图1中的d点时,θ角为-180°,此刻对应滑行车的行程为183.9m,再由图9b滑行车行驶法向加速度与位置关系可知,此行程时滑行车的行驶法向加速度An=3.4 m·s-2,此时滑行车受到的轨道支撑力为N=mw(An-g)=2.4mw,所以当车体运行至d点处时,受到的轨道支撑力仍为正即此处轨道仍受到滑行车向上的压力,这与滑行车的设计初衷相符即为了安全起见,当车身正面朝下此时乘客翻转了180°为头朝下,即使此刻乘客的安全护具出现问题,乘客也不会脱离开座椅出现坠落事故.

图9 滑行车切向速度、法向加速度与位置关系Fig.9 Relation between tangential velocity,vertical acceleration and position for roller coaster

3.3 人体感受情况

滑行车运行过程中,人体感受情况是对滑行车运行过程中车体的行驶加速度和人体自身重力加速度的综合感受.乘坐滑行车时人体的感受情况可分为,超失重和牵拉感.其中超失重感对应在人体坐标系下(即车体的切向和法向加速度所在坐标系见图1中的at和an)人体感受的an方向上的加速度之和,牵拉感对应人体感受的at方向上的加速度之和.

人体感受的超失重感可表示为

(9)

式中:an为滑行车行驶法向加速度.其为正时,人体感受为超重；为负时,人体感受为失重.当重力加速度分量gcosθ指向轨道时,人体感受为超重反之为失重,所以在式(9)中为+gcosθ.当车体静止且姿态角θ为0,即人体只在一个完整重力加速度g作用下时,人体的感受情况表现为正常,所以在式(9)中计算人体感受时需去掉一个重力加速度,式(9)中为-g.图10a为人体感受的超失重感.从图中可以看到,人体感受的最大失重为11 m·s-2(1.1 g),发生在8～8.5 s和22.5～23 s这两个0.5 s的时间段内,此处为滑行车进入立环之前的一段凸弧轨道.人体感受的最大超重小于60 m·s-2(6 g). 人体的牵拉感可表示为

(10)

式中：at为滑行车的行驶切向加速度,其为正时,人体感受为牵引；为负时,人体感受为回拉.当重力加速度分量gsinθ与车体前进方向一致时,人体感受为回拉,反之为牵引,所以在式(10)中为-gsinθ.atm为人体感受的牵拉感,其为正时,人体感受为牵引;为负时,人体感受为回拉.图10b为人体感受的牵拉感,从图中可以看到在滑行车运行过程中,车尾处乘客感受的牵引感最大,车头处乘客感受的回拉感最大,位于车体中点处乘客对牵引和回拉的感受小于车尾和车头.此外,从图10中还可以看到,位于车头处的乘客感受的最大超失重和牵拉感都大于位于中点和车尾位置乘客的感受情况,即在滑行车运动过程中,车头处乘客感受的刺激性最大.同时,atm和anm可反映出人体感受的自身所处姿态情况,如倾斜、水平或翻转的情况.

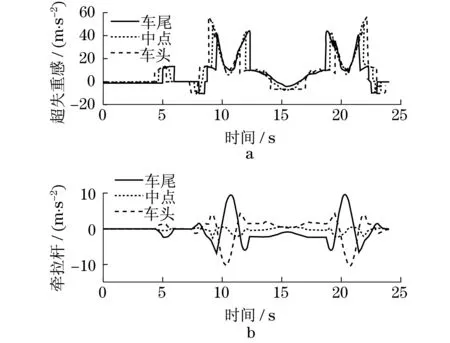
图10 人体超失重感Fig.10 Feeling of overweight and weightlessness

4 结论

根据滑行车轨道几何形状,计算出轨道的倾角、曲率、高度与轨道长度的关系曲线.将滑行车简化为考虑实际车长的柔性体,并建立其动力学方程,通过Simulink仿真计算,获取其行程、行驶速度、行驶加速度的时间历程及其运动参数随弧坐标s的变化关系,同时计算了滑行车运行过程中,人体的感受情况.主要结论如下:

(1) 滑行车轨道倾角θ(s)可较简便地描述轨道的形状特征.轨道采用弧坐标表示,建立滑行车动力学方程的方法较容易获取其运动参数随轨道位置变化的关系曲线,且此曲线对作为典型运动关联型设备的滑行车的设计、安全性评估等具有重要意义.

(2) 获取的滑行车的行驶速度、姿态角以及轨道的几何参数等为后续滑行车的随机振动模型的建立奠定了基础.

(3) 计算得到滑行车运行过程中人体的超失重、牵拉感且计算预测的人体感受和实际乘坐滑行车的感受完全吻合,为滑行车轨道设计和改进提供依据.

[1] 沈勇,刘志学,张宏伟.游乐设施作业与管理[M].北京:学苑出版社,2003.

SHENYong,LIU Zhixue,ZHANG Hongwei.The operations and management of Recreation facility[M].Beijing:Learning Centre Press,2003.

[2] 井科学.特种设备事故分析与对策[J].装备制造技术,2009(8):113-114.

JINGKexue.Accident analysis and measure of special equipment[J].Equipment and Manufacturing Technology,2009(8):113-114.

[3] PELLETIER A R,GILCHRIST J.Roller coaster related fatalities,United States,1994-2004[J].Injury Prevent,2005,11(5):309-312.

[4] BRAKSIEK R J,ROBERTS D J.Amusement park injuries and deaths[J].Annals of Emergency Medicine,2002,39(1):69-72.

[5] 梁朝虎,沈勇,秦平彦,等.滑行车类游乐设施动力学建模与仿真[J].中国安全科学学报,2007,17(9):14-20.

LIANG Chaohu,SHEN Yong,QIN Pingyan，et al.Dynamic modeling and simulating for amusement device as roller coasters[J].China Safety Science Journal,2007,17(9):14-20.

[6] 汪惠群,郑建荣.大型游艺机——过山车的安全性分析[J].中国安全科学学报,2006,16(2),43-46.

WANG Huiqun,ZHENG Jianrong.Safety analysis of roller coaster[J].China Safety Science Journal,2006,16(2),43-46.

[7] 郑建荣,汪惠群.过山车虚拟样机的建模与动态仿真分析[J].机械设计与研究.2004,20(2):74-77.

ZHENG Jianrong,WANG Huiqun.Modeling and dynamic analysis of roller coaster using virtual prototype[J].Machine Design and Research,2004,20(2):74-77.

[8] WANG Hongjun,WANG Hongfeng.The dynamic simulation model of suspended roller coaster based on virtual prototype [J].2010 International Conference on Educational and Information Technology,2010,193-196.

[9] TENG Rumin,WEI Guan,GAO Shunde et al.Dynamic modeling and simulation of Roller Coaster.2010 International Conference on Computer Application and System Modeling.2010,340-342.

[10] 哈尔滨工业大学理论力学教研室.理论力学Ⅰ[M].第6版.北京:高等教育出版社,2002.

Harbin Institute of Technology Theoretical Mechanics Teaching and Research Section.Theoretical mechanics(Ⅰ)[M].6th ed.Beijing:Higher Education Press,2002.

[11] 余志生.汽车理论[M].第3版.北京:机械工业出版社,2000.

YU Zhisheng.Automobile theory[M].3th ed.Beijing:China Machine Press,2000.

[12] AHN H S,CHEN Yangquan,MOORE K L,et al.Stability analysis and control of repetitive trajectory systems in the state-domain:roller coaster application[J].22nd IEEE International Symposium on Intelligent Control Part of IEEE Multi-conference on Systems and Control.2007,220-225.

Dynamical simulation on roller coaster during traveling process

ZHU Yu-tian,ZHENG Li-hui,LIU Zhao

(College of Mechanical and Energy Engineering,Tongji University,Shanghai 201804)

According to the track shape,the geometric parameters of the roller coaster track are calculated.By using SimulinkTMsoftware for a dynamical model,the traveling route,velocity,acceleration,posture in different positions of the roller coaster,together with the relation between kinematic parameter and track position,are simulated.Meanwhile,the reactions from human body are obtained.In comparison with the simulation results from ADAMSTM model,the credibility of the proposed model is verified.Therefore,a new method is postulated on kinematic parameter simulation.Furthermore,the simulation results and analysis method set a reference to design and safety evaluation on roller coasters.

roller coaster; flexible body;human reaction; simulink

朱玉田(1967-),男,博士,教授.E-mail:yutianzhu@tongji.edu.cn

TH 12

A

1672-5581(2016)02-0131-06