无喷管助推器侵蚀燃烧模型对比研究

黄礼铿+杨玉新+霍东兴+马利峰

摘要： 侵蚀燃烧对无喷管助推器的性能有着至关重要的影响。 为了在无喷管助推器设计中准确预测其性能， 在分析侵蚀燃烧机理的基础上， 利用一维非定常变截面内弹道计算程序， 采用几种典型的侵蚀燃烧模型对单燃速锥柱形装药和双燃速串装锥柱形装药发动机的特性进行分析。 研究表明， 文中推进剂在单燃速锥形装药发动机中表现出较弱的负侵蚀效应， 采用无负侵蚀效应的侵蚀燃烧模型的预示结果好于带有负侵蚀效应的侵蚀模型， 其中LenoirRobillard模型的预示精度最高。 而双燃速串装发动机中由于燃气流速较小的范围更大， 负侵蚀效应影响较大， 只有使用具有负侵蚀效应的Greatrix模型才能得到较为准确的预示结果。

关键词： 内弹道计算； 无喷管助推器； 侵蚀燃烧； 双燃速串装药柱

Abstract： Erosive burning has significant influence on the performance of nozzleless booster. In order to accurately assess its performance in the design of nozzleless booster， based on the analysis of erosive burning mechanism， the characteristics of single burning rate grain nozzleless booster and series dual burning rate grain nozzleless booster are analyzed by using onedimensional unsteady internal ballistic simulation and several erosive burning models. The results show that the single burning rate grain nozzleless booster exhibits weak negative erosive burning， thus erosive burning models without negative erosion effect gets better prediction results than those with negative erosion effect， and LenoirRobillard model has the best prediction accuracy. As the low crossflow velocity region of series dual burning rate grain nozzleless booster is much wider， the influence of negative erosion effect is greater， only using the Greatrix model with negative erosion effect can get more accurate prediction results.

Key words： internal ballistic calculation； nozzleless booster； erosive burning； series dual burning rate grain

0引言

整体式固体火箭冲压发动机采用无喷管助推器时， 与有喷管发动机方案相比， 最终飞行速度提高3%～13%， 研制成本降低10%～20%[1]； 且使用无喷管助推器无抛出物， 消除了对载机及阵地的潜在危害， 增加了工作可靠性。 因此， 无喷管助推器得到越来越广泛的应用。

无喷管助推器通常是锥柱形装药， 长径比一般大于5， 气流在通道内依靠加质不断加速， 在通道后部达到音速， 推进剂燃速由于高速燃气带来的侵蚀燃烧而大大增加， 特别是喉道处的侵蚀燃烧非常严重。 推进剂的燃速决定了助推器的推力水平和药柱燃烧时间， 同时也决定了喉部面积的变化趋势， 而喉部面积的变化又反过来影响助推器压强， 影响推进剂燃速。 因此， 侵蚀燃烧在无喷管助推器的工作过程中起着至关重要的作用， 研究无喷管助推器的侵蚀燃烧规律具有重要意义。

目前针对侵蚀燃烧现象已经开展大量研究， 并提出许多侵蚀燃烧模型。 早期的研究认为， 产生侵蚀燃烧的主要原因在于流经燃面的燃气流加速了火焰区对推进剂燃面的传热作用。 横向流速愈大， 燃速也愈大， 从而影响发动机性能。 根据这一规律， Wimpress[2]， Green[3]和Kreidler[4]分别提出以气流速度u及燃气质量流率G=ρu表示的侵蚀函数公式。 King[5-6]把侵蚀燃烧速率与初始燃烧的比值作为压强、 横向流速和推进剂颗粒直径的函数， 再根据压强、 瞬间推力与时间的函数关系直接得出瞬间燃烧速度。 由于侵蚀燃烧效应与发动机尺寸相关， 侵蚀效应随药柱内孔直径增大而减小， 因此Lenoir和Robillard[7]在侵蚀模型中加入药柱内孔直径的影响。 通常固体推进剂的燃速随着压强和燃气流速的增加而增加， 且总燃速只有在燃气速度大于一定阈值时才会大于基础燃速。 Marklund和Lake[8]发现当燃气速度小于阈值速度时， 总燃速可小于基础燃速， 这被称为负侵蚀燃烧。 Sabdenov和Erzada[9-10]研究了负侵蚀燃烧的机理， 并利用理论分析方法对负侵蚀燃烧进行研究， 结果表明降低推进剂初温可以减弱负侵蚀燃烧效应。 张方方等[11]研究了高低温下推进剂侵蚀燃烧效应对发动机性能的影响。 Kulkarni等[12]利用部分燃烧技术对侵蚀燃烧过程进行研究， 并基于试验结果对侵蚀燃烧常数进行改进， 提高了大尺寸发动机的性能预示精度。 Sheikholeslam[13] 利用试验研究分析了长径比对固体推进剂侵蚀燃烧的影响。

航空兵器2016年第5期黄礼铿等： 无喷管助推器侵蚀燃烧模型对比研究由于固体推进剂的侵蚀燃烧与推进剂本身特性和发动机装药结构密切相关， 根据不同侵蚀燃烧理论提出的侵蚀燃烧模型只在各自的适用范围内具有较高精度。 本文针对研究中使用的推进剂和发动机装药结构， 采用一维非定常内弹道性能计算研究推进剂的侵蚀燃烧机理和规律， 将不同侵蚀燃烧模型的性能预测结果与试验进行对比， 以便在无喷管助推器设计中选择合适的侵蚀燃烧模型。 并对双燃速串装锥柱形装药发动机的侵蚀燃烧特性进行分析， 以便为高性能无喷管助推器的设计奠定基础。

1一维非定常内弹道计算

1.1基本方程

无喷管助推器大都采用圆柱内孔燃烧装药， 出口部位有扩张锥。 在无喷管助推器工作过程中， 燃气通道、 喉部面积、 出口面积随时间快速增大， 因此， 准确计算无喷管助推器非定常过程中参数的变化规律是很重要的。

1.3数值计算方法

对于方程（1）的数值求解， 由于加质加热使得方程刚性过强， 为保证求解过程的数值稳定性， 时间方向采用显式迭代需要的时间步长过小， 使得计算代价难以承受。 因此在时间方向采用LU-SGS隐式时间离散格式， 避免方程呈刚性。 空间离散采用Roe格式， 并通过MUSCL插值方法获得高阶空间离散精度， 使方程组的解具有良好的保单调性。

求解的初始条件：

计算初始（t=0）， 整个通道中气体处于静止状态， 气体压强为环境压强， 气体温度为推进剂初温， 气体速度为0。

求解的边界条件：

（1） 上游边界条件（即x=0处）

燃气流速为0， 温度为燃气总温， 密度由外推得出。

（2） 下游边界条件（即x=L处）

当气流速度为亚音速时， 出口压强为环境压强， 流速和密度由外插确定； 当气流速度为超音速时， 全部参数由外插确定。

另外， 对于燃气气体状态的计算，仍采用理想气体状态方程p=ρRT， 但状态方程的气体常数通过化学平衡计算得到， 使其成为温度和压强的函数， 更接近于实际情况。

2侵蚀燃烧模型

通常认为侵蚀燃烧是由传递到药柱表面的热量增加导致的， 热传递的增加导致推进剂蒸发更快， 给火焰区增加了更多的燃料和氧化剂。 为了解释传递到药柱表面热量增加这一现象， 已经提出了很多相关的理论， 主要分为三类： 第一类理论认为侵蚀燃烧是由主流通过火焰区向药柱表面传递更多的热量导致的； 第二类理论认为侵蚀燃烧是由湍流的输运作用， 使得主流或者边界层内的热量更多地传递到药柱表面导致的； 第三类理论认为侵蚀燃烧是由于主流将扩散火焰弯曲到药柱表面， 使热量在离药柱表面更近的地方释放导致的。

根据不同的侵蚀燃烧理论， 发展了很多侵蚀燃烧模型。 Green[3]， Lenoir和Robillard[7]认为侵蚀燃烧是由于从主流向药柱表面传递额外热量导致的， 属于第一类理论的支持者。 Green认为较高的主流速度降低了边界层厚度， 药柱表面的热量来源于主流， 因此边界层越薄， 传递到药柱表面的热量越多， 而完全没有考虑扩散火焰的影响， 其构造的侵蚀燃烧模型表示如下：

3算例及结果分析

3.1发动机参数

由于双燃速串装药柱的无喷管助推器可使压强曲线更为平直， 使壳体强度利用率提高， 提高发动机性能。 因此分别对单燃速装药和双燃速串装药柱无喷管助推器进行试验研究， 并利用一维非定常内弹道计算方法结合不同侵蚀燃烧模型进行发动机性能分析。 两种装药方案均采用圆柱内孔装药， 其中装药燃烧室的主要尺寸为： 药柱外径Φ180 mm， 内孔直径Φ50 mm， 药柱总长1 300 mm（含喷管）； 分段串装结构在药柱后部装填一段低燃速药柱， 尺寸同单燃速装药， 发动机装药为HTPB推进剂。

3.2单燃速装药发动机计算结果

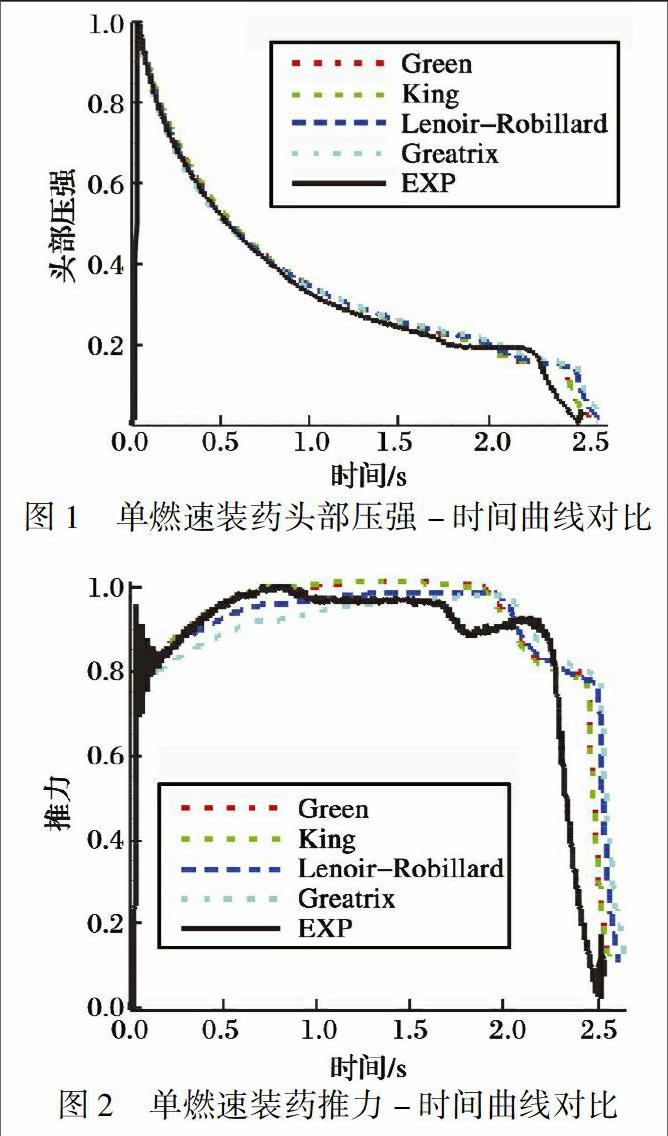
利用一维非定常内弹道计算程序对单燃速装药无喷管助推器性能进行预示， 不同侵蚀燃烧模型与试验结果的对比如图1～2所示， 其中压强和推力均利用最大值进行无量纲处理。 可以看出， 几种模型的预示结果与试验结果吻合较好， 预示的压强峰值较为一致。 由于内弹道计算没有考虑点火燃烧和药柱变形影响， 使得预示的发动机工作时间偏长， 且一维计算不能考虑流动的三维影响， 预示结果不能体现冲压喷管暴露的影响。

单燃速装药燃面退移规律和燃速对比见图3～4。 可以看出， Green模型和King模型给出了相同的侵蚀规律， 其侵蚀燃烧较强， 燃面退移较快， 预示的推力较大。 LenoirRobillard 模型考虑了推进剂的基础燃速、 燃气通道直径、 热传递的影响， 预示的结果与试验结果吻合最好。 Greatrix模型在考虑推进剂基础燃速、 燃气通道直径和热传递影响的基础上， 还考虑了负侵蚀影响， 降低了燃气流速较低时的推进剂燃速， 使得燃面退移变慢， 发动机推力较低， 工作时间变长。 由此可见， 试验采用的单燃速装药发动机没有表现出明显的负侵蚀现象， 在性能预示时不需要考虑负侵蚀影响。

3.3双燃速串装药柱发动机计算结果

可以看出， Green模型、 King模型和LenoirRobillard模型预示的工作后段压强偏高， 推力偏大； Greatrix模型则得到了与试验较为一致的结果。 同样， 由于没有考虑点火燃烧和药柱变形， 预示工作时间偏长。

双燃速串装药柱发动机燃面退移规律和燃速对比如图7～8所示。 可以看出， 双燃速串装药柱的低燃速推进剂燃烧较慢， 形成喉径， 使得压强变化更平缓。 Green模型和King模型预示的燃速和燃面退移规律在工作初始时较为一致， 但King模型燃速降低更快， 在1.5 s时King模型预示燃速小于Green模型。 LenoirRobillard模型预示的燃速在工作初始时较大， 但减小最快。 工作0.3 s时， LenoirRobillard模型预示的燃速最大； 工作0.9 s时， LenoirRobillard模型预示燃速减小至与Green模型相近； 在1.5 s时进一步减小， 与King模型和Greatrix模型预示燃速相近。 由于燃气通道内燃气流速较低， 考虑负侵蚀影响的Greatrix模型预示的燃速在整个工作过程中都最低， 燃面退移最慢。 可见对于双燃速串装药柱发动机， 由于燃气通道内燃气流速较低， 负侵蚀影响较大， 考虑负侵蚀影响的Greatrix模型预示的结果与试验结果吻合最好。

4结论

通过对单燃速装药和双燃速串装药柱无喷管助推器的一维非定常内弹道性能预示对比， 得出以下结论：

（1） 采用的一维非定常变截面流动模型对无喷管固体火箭发动机实际工况描述正确， 数值预示精度满足无喷管固体火箭发动机设计要求。

（2） 由于单燃速装药发动机燃气通道内燃气加速较快， 燃气流速较低， 范围较窄， 负侵蚀燃烧效应的影响不明显， 而双燃速串装药柱发动机燃气流速较低， 范围较宽， 负侵蚀燃烧影响较大。

（3） 研究采用的Green模型、 King模型和LenoirRobillard模型对没有明显负侵蚀燃烧现象的发动机性能预示较为准确， 其中LenoirRobillard模型预示精度最高。

（4） 对于双燃速串装药柱发动机， 考虑推进剂基础燃速、 燃气通道直径、 热传递以及负侵蚀燃烧影响的Greatrix模型能够准确描述推进剂的侵蚀和负侵蚀燃烧现象， 具有较高的精度， 满足双燃速串装药柱发动机设计的需求。

参考文献：

[1] Timnat Y M.Advanced Chemical Rocket Propulsion[M].London： Academic Press， 1987： 107-118.

[2] Wimpress R N. Internal Ballistics of SolidFuel Rockets[M].New York： McGrawHill Book Company， 1950.

[3] Green L， Jr.Erosive Burning of Some Composite Solid Propellants[J].Journal of Jet Propulsion， 1954， 24（1）： 9-15.

[4] Kreidler J.Erosive Burning： New Experimental Techniques and Methods of Analysis[C]∥Solid Propellant Rocket Conference， Palo Alto， California， 1964.

[5] King M K.Erosive Burning of Composite Solid Propellants： Experimental and Modeling Studies[J]. Journal of Spacecraft and Rocket， 1979， 16（3）： 154-162.

[6] King M K.Erosive Burning of Solid Propellants[J]. Journal of Propulsion and Power， 1993， 9（6）： 785-805.

[7] Lenoir J M， Robillard G.A Mathematical Method to Predict the Effects of Erosive Burning in SolidPropellant Rockets[C]∥Proceedings of the Sixth Symposium （International） on Combustion， Elsevier， 1957， 6（1）： 663-667.

[8] Marklund T， Lake A. Experimental Investigation of Propellant Erosion[J]. ARS Journal， 1960， 30（2）： 173-178.

[9] Sabdenov K O， Erzada M.Analytical Calculation of the Negative Erosive Burning Rate[J]. Combustion， Explosion， and Shock Waves， 2013， 49（6）： 690-699.

[10] Sabdenov K O， Erzada M.Mechanism of the Negative Erosion Effect[J]. Combustion， Explosion， and Shock Waves， 2013， 49（3）： 273-282.

[11] 张方方， 侯健， 魏平， 等.存在侵蚀燃烧的发射药高、 低温内弹道性能研究[J].弹箭与制导学报， 2012， 32（1）： 145-148.

[12] Kulkarni A R， Dalal K S， Phawade P A， et al.Erosive Burning and Its Applications for Performance Prediction[J]. Defence Science Journal， 1993， 43（2）： 159-165.

[13] Sheikholeslam M R Z， Kazemi D， Amiri H.Experimental Analysis of the Influence of Length to Diameter Ratio on Erosive Burning in a Solid Tubular Propellant Grain[C]∥Applied Mechanics and Materials， Switzerland： Trans Tech Publications， 2012， 110： 3394-3399.

[14] 潘旭东.无喷管固体火箭发动机内弹道计算[D]. 西安： 西北工业大学， 2006.

[15] Lawrence W J， Matthews D R， Deverall L I.The Experimental and Theoretical Comparison of the Erosive Burning Characteristics of Composite Propellants[C]∥3rd Solid Propulsion Conference， Atlantic City， New Jersey， 1968， 67（5）： 2590-2601.

[16] Greatrix D R.Model for Prediction of Negative and Positive Erosive Burning[C]∥42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit， Sacramento， California， 2006， 53： 13-21.