EGARCH-M模型在证券时间序列分析中的应用

杨世康，邓世权，童汝超，龙见远，吴巧霞

（凯里学院，贵州 凯里 556011）

EGARCH-M模型在证券时间序列分析中的应用

杨世康，邓世权，童汝超，龙见远，吴巧霞

（凯里学院，贵州 凯里 556011）

证券综合指数的对数收益率的折线图反映收益率的波动呈现出在一段时间内波动比较大，一段时间波动比较小，方差随着时间的变化而变化。在对时间序列数据进行研究的时候，通常假设随着时间的变化方差不会发生变化。但是在关注预测的精确程度时，需要了解方差的大小。文章用Eviews软件对上证综指日收盘价的对数收益率建立EGARCH-M模型，对收益率序列呈现出的波动聚集性，杠杆效应、风险与收益的关系等特征进行了分析，最终对波动率进行预测，结果表明EGARCH-M模型充分描述了波动性聚类的特点，只用很少的参数就可以把实际数据拟合得很好。该模型形式简单，容易估计，提高了对方差的预测精度，对收益率波动率建立模型对于宏观经济理论和金融理论有重要的意义。

对数收益率；风险；聚类；EGARCH-M；杠杆效应

1986年Bollerslev[1]提出了广义的ARCH模型（Generalized ARCH Model, GARCH）GARCH模型在实际中有广泛的应用。金融资产的收益率应当与风险成正比，将收益率的条件方差或者条件方差的其他形式加入到其均值方程中，在GARCH模型的基础上，出现了均值GARCH模型（GARCH-M）。相关研究表明，金融资产价格的下跌比相同幅度的价格上涨对资产价格波动的冲击影响更大，即“杠杆效应”，所以人们提出了非对称ARCH模型,指数GARCH模型（Exponential GARCH,EGARCH）就是其中的一种[2]。本文融合了GARCH-M模型和EGARCH模型，在GARCH-M模型中加入非对称项，建立EGARCH-M模型对我国上证综合指数的日对数收益率进行了分析。

1 EGARCH-M模型

1.1 ARCH效应

（1）ARCH效应的描述。金融资产价格或者收益率等高频数据表现出在一个大的波动后面常常会跟着另一个大的波动，而在一个小的波动后面常常会跟着另一个小的波动现象。这种现象称之为ARCH效应[3]。

（2）残差平方相关图。残差平方相关图可以用于检测残差序列是否存在ARCH效应，如果残差在所有滞后阶数上的自相关函数和偏自相关函数统计上都显著地异于零，而且其相应的Q统计量也显著，说明存在ARCH效应，否则说明不存在ARCH效应[4]。

1.2 GARCH-M模型[5]

（1）GARCH模型。当检测到ARCH效应时可以建立GARCH模型来拟合原序列。在GARCH系列模型中一个形式简单且应用广泛的是GARCH（1，1）模型，其形式如方程（1）所示。

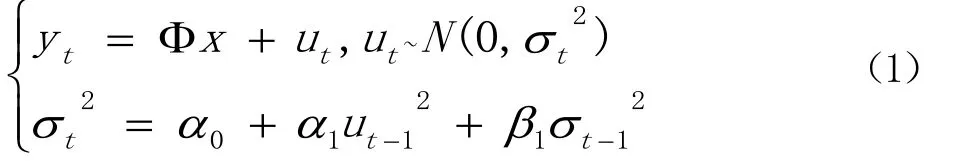
其中第一个方程称为均值方程，第二个方程为条件方差方程。

（2）GARCH-M模型。在一般的GARCH模型中，假设金融序列的条件均值是不变的。但在很多情况下，金融资产的收益率常常与投资风险紧密相连。GARCH-M模型，在GARCH模型的均值方程中加入衡量风险的GARCH项。GARCH-M模型的表达式如方程（2）所示。

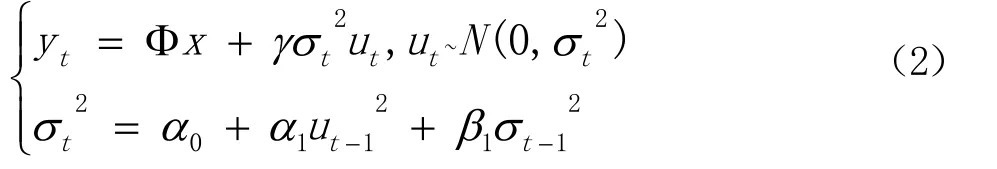
1.3 EGARCH-M模型[6]

为了能够解释金融时间序列经常存在的“杠杆效应”即资产价格的下跌比同样程度的价格上涨产生的波动更大，人们提出了非对称的GARCH模型，EGARCH模型就是其中的一种。EGARCH-M模型即指数GARCH-M模型，其方差等式分析的不是σt2而是1n σt2。

2 实证分析

2.1 建立随机游走模型

首先生成SZZS的自然对数序列。把上证综指序列用“SZZS”表示。求SZZS的自然对数公式为：

对SZZS建立如方程（4）随机游走模型：

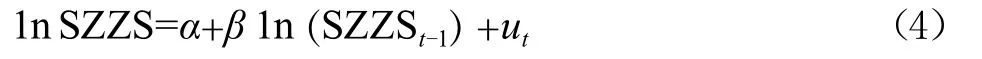
对方程（4）进行估计，方程估计 结 果 显 示， F 统 计量显著表明方程整体上是显著的，R2=0.998 177，表明方程拟合效果比较好。

首先生成残差序列，其折线图回归方程的残差表现出波动聚集性，大的波动后面伴随着较大波动，小的波动后面伴随着较小的波动，该特征表明存在ARCH效应。

2.3 建立EGARCH-M模型

在本文中用SZZS的对数收益率建立模型。在研究过程中，不直接对SZZS建立模型，而是对其对数收益率建立模型，因为人们发现上证综指的日收盘价的序列是不平稳的，但它的对数收益率是平稳的，便于建立模型来进行研究。本文中用rt来表示SZZS的对数收益率。如方程（5）所示：

2.3.1 对数收益率序列特征分析

（1）对数收益率序列相关图。rt.的自相关函数和偏自相关函数绝大多数都在95%的置信区域内时Q统计量的值也不显著，因此可以认为rt不存在自相关。

（2）对数收益率序列的直方图和基本统计量信息。可以看到rt是不对称的，而且其左尾拖得比较长，序列rt的偏度为-0.097 798，也表明序列rt呈左偏分布的。序列rt的峰度为6.961 026，其峰度值大于正态分布假设的3，从而表明其分布呈“尖峰、厚尾”的特点。序列rt的J-B统计量非常大，其相应的概率值非常小，所以可以认为rt不服从正态分布。序列rt的均值为0.000 697，非常接近于0。

2.3.2 EGARCH-M模型估计

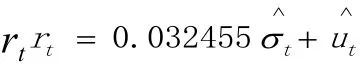
均值方程：

其中假定误差项ut服从t分布，自由度为5.297 290，z统计量为9.388 465。

条件方差方程：

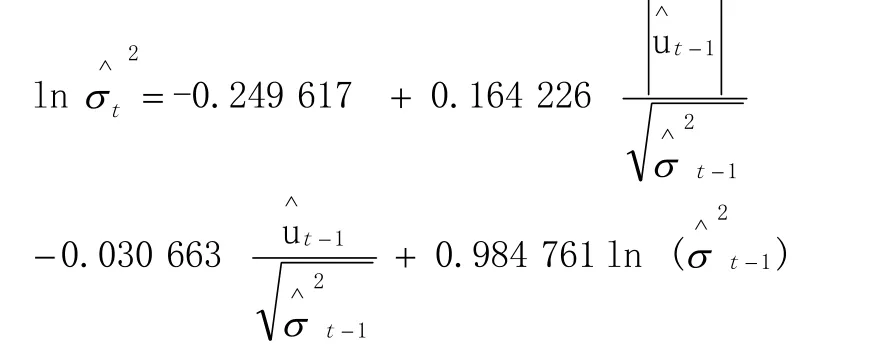
AIC准则=-5.632 146，SC准则=-5.619 789

从所估计的均值方程可以看到，的系数为0.032 455，表明当市场中预期风险增加1%时，会导致预期收益率也相应增加0.032 455%。

条件方差方程中非对称项的估计值为-0.030 663，小于零且显著，从而表明坏消息对波动有杠杆效应。EGARCH-M的信息影响曲线可以看到在0的左边（z＜0）曲线的斜率的绝对值比较大，而在0的右边（z＞0）曲线斜率的绝对值比较小，从而说明负的冲击比正的冲击对波动性影响更大。

3 结语

本文用ARCH模型的变形即EGARCH-M模型对SZZS的波动聚集性、杠杆效应、收益率与风险的关系等进行了很好的描述与分析，可以在时间序列的预测方面有较好的表现。借助EViews软件，可将ARCH模型应用于金融的时间序列问题的研究和预测。然而ARCH模型有很多变形，根据样本的不同，需要选择合适的模型和参数，有时对模型参数的选择得反复尝试，最终选择正确的模型。

[1]BOLLERSLEV T, MEDDAHI N. Realized volatility forecasting and market microstructure noise[J]. Econometrics,2011（160）：220-234.

[2]潘红宇.金融时间序列模型[M].北京：对外经济贸易大学出版社，2008.

[3]张成思.金融计量学：时间序列分析视角[M].北京：中国人民大学出版社，2012.

[4]彭作祥.金融时间序列建模分析[M].成都：西南财经大学出版社，2006.

[5]易丹辉.时间序列分析：方法与应用[M].北京：中国人民大学出版社，2011.

[5]吴怀宇.时间序列分析与综合[M].武汉：武汉大学出版社，2004.

[6]任英华.EViews应用实验教程[M].长沙：湖南大学出版社，2008.

Application of EGARCH-M model in the stock time series analysis

Yang Shikang, Deng Shiquan, Tong Ruchao, Long Jianyuan, Wu Qiaoxia
（Kaili University, Kaili 556011, China）

From the line chart of Logarithmic yield of stock composite index, it can be seen that the fluctuation of yields shown relatively large in a period of time and relatively small in another period, which shows that the variance changes with time changes. In the study of time serious data, it is usually assumed that the variance will not change as time changes. But when we concern about the degree of accuracy of the forecast, we need to know the size of the variance. The article use Eviews software to build EGARCH-M model for the logarithm yield of Shanghai composite index day closing price, to analyze features of volatility clustering showed in yield sequence, leverage effects, the relationship between risks and returns, and finally make a forecast to volatility. The results show that the EGARCH-M model adequately describes the characteristics of volatility clustering. With only a few parameters that can fit the actual data well. The form of the model is simple, easy to estimate, which improves the forecast accuracy of variance. It has a great importance in the building of model of yield volatility and macroeconomic theory and financial theory.

logarithmic yield; risks; clustering; EGARCH-M; leverage effects

杨世康（1988— ），男，贵州凯里，硕士；研究方向：无线通信，个人通信以及认知无线电频谱分配等。