城市暴雨沥涝数学模型的研究与应用
2016-12-09李大鸣胡永文范丽虹
李大鸣,胡永文,王 笑,范丽虹
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
城市暴雨沥涝数学模型的研究与应用
李大鸣,胡永文,王 笑,范丽虹
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
为解决城市沥涝问题,以二维非恒定流方程为基本控制方程,按照水量平衡法改进的有限体积法思想,结合城市复杂的汇流特点,提出了一种分区分层的计算模式,构建了二维城市暴雨沥涝数学模型,包含了社区汇流、路网汇流、管网汇流和河道汇流4个计算模块。以天津市示范区段为研究对象,依次模拟了2009—2015年10次降雨过程,分析对比了验证点积水水位和湘江道的津河液位。模拟结果显示,河道液位模拟值与实测值变化趋势基本一致,两者平均值之间的误差均<10 cm, 表明了模型具有一定的计算精度,可用于城市内涝监测预报,同时也为城市暴雨沥涝数学模型研究提供了新的方法和思路。
暴雨沥涝;水量平衡;有限体积法;分区分层;城市内涝
1 研究背景
天津市位于海河水系尾闾,是九河下梢之地,上游来水面积大,而入海口小,排水不畅。近年来随着天津市的迅速发展,不透水面积所占比重越来越大,地表对雨水的截留和下渗能力降低,雨水产汇流时间缩短,极易造成积水[1]。当积水深度达到一定程度时,就会给城市正常运转造成影响,甚至造成损失[2]。城市暴雨导致的积涝灾害频发和“海绵城市”概念的提出使沥涝问题的解决变得越来越重要。
国外很多城市的雨洪模型已经比较成熟并已在实际中得到应用,其中几个比较有名的应用软件有Mike,Wallingford的Infoworks和DHI的Mouse[3]。我国岑国平等[4-6]、仲志余[7]、周玉文等[8]、徐向阳[9]都对城市雨水径流计算模型进行了研究。当下城市暴雨沥涝数学模型大多基于水动力学模型构建[10-14]。本文采用有限体积法建立了分区分层的城市暴雨沥涝数学模型,分为社区汇流、路网汇流、管网汇流和河道汇流4个模块。4个模块在网格的划分上相对独立,在雨水量交换上耦合成为一个整体。
2 分区分层计算模式
2.1 研究区域概况
模型研究区域位于天津市南开区内,属于著名的季风气候区,全年降雨多集中在7,8月份,易造成内涝积水。地物地貌复杂多变,河网、路网纵横交错,人口相对集中造成了区域内部土地利用类型多种多样,建筑高低不一,易导致局部积水较为严重现象的发生。
2.2 分区分层、立体多重的网格形式
由于研究区域下垫面情况复杂,网格不能进行统一的划分,有针对地把单元划分为三角形、四边形、五边形的网格,使用放宽和加密网格的办法准确地反应其特征。此外,河网、管网、路网以及社区的分布形式多样,这些因素对暴雨径流有着较大的影响。考虑这些因素并对该区域采用分区分层、立体多重的方法进行划分。由于管网地下埋布情况复杂,所以将管网网格划分等同于路网。分区为河网、路网、管网和社区中分区收水,以及各自相对独立的网格划分体系,可以逐区域计算模拟;分层主要指空中雨量分布层、地表河网、路网、社区水量分水层、地下管网水量分布层;立体多重主要指在同一平面空间位置上考虑路网、管网或立体交通、路下暗河等多重网格形式,使单元重叠划分。
模型河道型单元数为104个,道路型单元数为1 116个,社区型单元数为1 081个,计算区域东西宽5.93 km,南北长2.38 km,覆盖面积约为6.56 km2。区域网格划分见图1。
2.3 模块的模化及在水量交换上的耦合
暴雨沥涝模型的计算分为路网、社区、河网、管网4个模块。针对4个模块的特性采用不同的模化方法,模化示意图见图2。
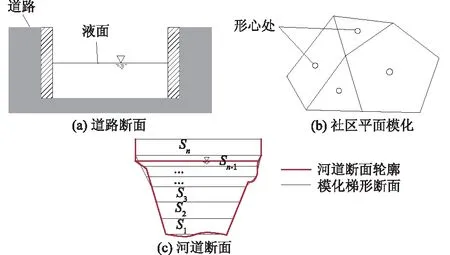
图2 模块模化示意图Fig.2 Sketch map of modeling
路网层模型建设主要以立体路网之间、路网与管网、路网与社区之间的水量交换为目标。水量交换的方式主要有陡坡汇流、垂直井汇或涌水、社区旁侧汇流或分流等。由于道路宽度不同,路网的宽度一般由其所在的网格尺寸所决定。由于路面起伏较小,可以将路网断面模化成矩形断面,如图2(a)所示,可以根据水深及其对应的断面尺寸计算出断面的过流量。
社区层模型主要以社区与管网、社区与路网水量交换为研究重点,如图2(b)所示。水量交换方式主要有整体社区与周边路网水量交换、实时局部社区水量分布、社区与管网区划汇流等。社区内下垫面情况比较复杂,有高层建筑,也有道路、植被、空地等。根据社区地貌资料进行网格划分,形心点处的水位作为单元的平均水位,进一步可得到每一个单元的总水量。
河网层模型以管网和河网之间的水量交换为主要目标。模型建设以限流、控流和调节为条件并建立泵站抽水与自排相结合的排水模式。河网模化是将河道断面模化成若干个小的梯形断面,如图2(c),根据各个部分的过流量得出断面总流量。
管网层模型建设以河网出流口、路网入流口、社区汇流为重点研究目标。路面水体与管道水体的交换会出现2种情况,即下泄和上涌情况,如图3所示。
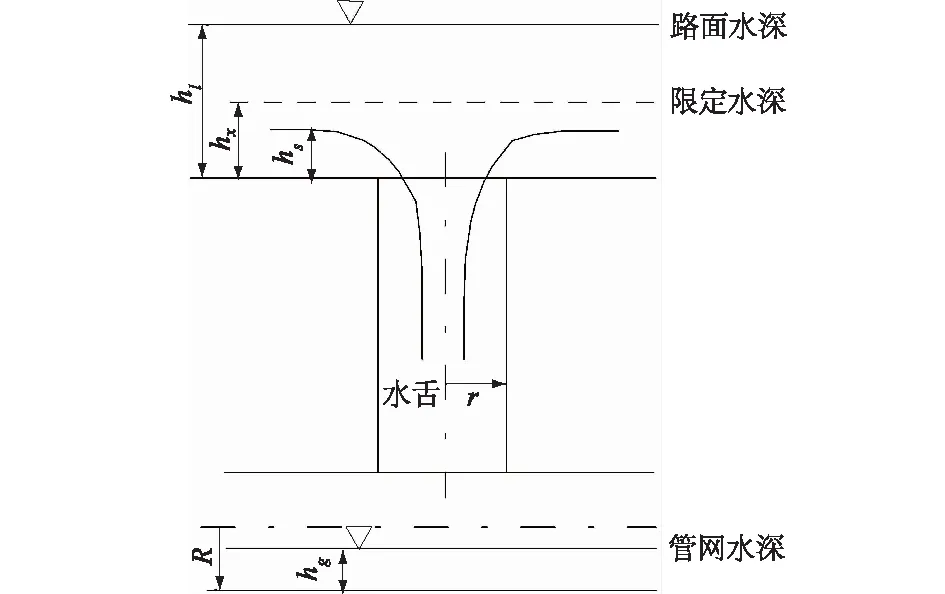
图3 路网管网水量交换示意图Fig.3 Sketch map of water exchange between road network and pipe network
下泄情况:当管道为无压流即2R>hg时,路面水体会通过雨水井口流入地下管网,设路面水深hl等于井口半径r时,此时路面水深等于限定水深hx,对应的水舌厚度为hs。当hl=hs
上涌情况:地下管网为有压流时,水流通过雨水井口上涌到地面,流量采用淹没孔口出流方式计算。地下管网向河网排水有2种方式,一种是自排水,一种是泵排水。
3 数学模型理论
3.1 模型基本控制方程
天津市暴雨沥涝数学模型模拟的对象主要包括河网、路网、管网和社区,基本控制方程为平面二维非恒定流方程,具体公式如下。
水流连续方程:
(1)
水流动量方程:
(2)
(3)
式中:H为水深(m);Z为水位(m),Z=Z0+H,Z0为底高程(m);q为源汇项(m3/s);M,N分别为x,y方向上的单宽流量(m2/s);u,v分别为x,y方向的平均流速(m/s);n为糙率;g为重力加速度(m/s2);t为时间(s);M=Hu,N=Hv。
3.2 水量平衡改进的有限体积法
应用有限体积法进行模型计算的优点在于将方程进行离散时能够保证在任一组控制体内均守恒。但由于计算模式的不足,常常会引起某些单元体出现水量不平衡的现象,即单元体出现入流量与出流量不相等的情况,会引起模型总水量的偏差,本节将对此部分进行改进和提高(时间t单位为s,水深H单位为m,流量Q单位为m3/s)。
模型应用无结构不规则网格进行前期处理,整个模型网格包括三角形、四边形及五边形。以图4为例进行说明,其中单元O为中心网格,与A,B,C,D 4个网格毗邻,整个计算模式以t,t+dt,t+2dt3个时间步长节点为一个单位时间计算过程(依照方程离散时的格式进行选取),整个时间范围内依次重复同一时间层面的处理过程。假定t时刻单元O,A,B,C,D内水深分别为H,Ha,Hb,Hc,Hd。
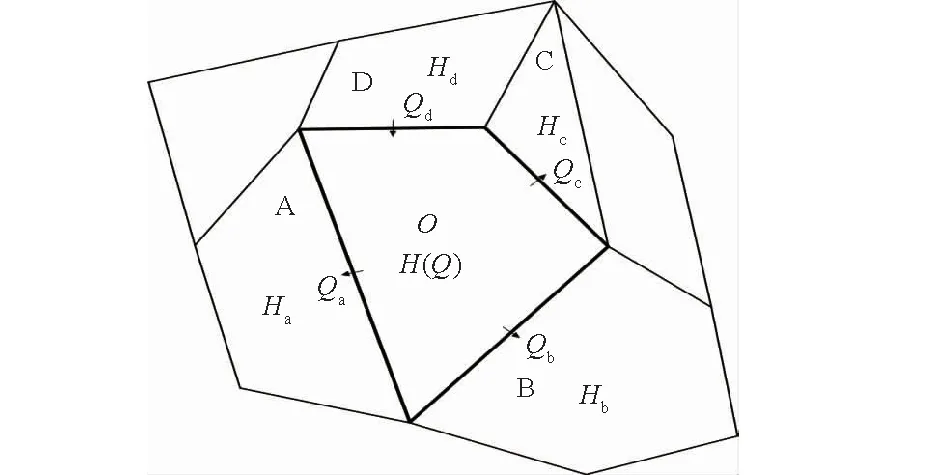
图4 水量交换示意图Fig.4 Sketch map of water change
当单元格内出现负水深时,将水深值赋值为0会增加各单元格之间的水量交换,从而导致不平衡现象的出现,引起虚假流动。对此模式进行改进主要分如下3个步骤。
(1) 当计算t+2dt时刻单元O内水深为负时(假定此时出现的负水深为-H),对计算模式进行修正,重新计算t+dt时刻的出流,由于单元O对单元A,B,C的出流是各个单元之间的水头差(即H-Ha,H-Hb,H-Hc)作为水量交换的比例,所以可以把所得的负水深(-H)按比例分配到出流Qa,Qb,Qc进行水量的缩减,重新得到此时的出流Qa1,Qb1,Qc1,保证单元格O不出现负水深。
(2) 步骤1中只对出流进行修正而未对入流进行处理,在t+dt时间层面上对不同单元格的出流进行修正的同时,相当于对其相邻的单元的入流也进行了修正,假定此时修正后的入流为Qd1,按照此时单元O向A,B,C单元泄流的比例重新分配Qd1到A,B,C单元中,则出流值修正值分别为Qa2,Qb2,Qc2,对流量进行修正时保证Qa2≤Qa,Qb2≤Qb,Qc2≤Qc。
(3) 应用步骤2中得到的出流对单元O的入流重新进行修正,将入流量按比例重新分配给此时单元O的出流,保证其出流量不大于连续方程的计算值,最终达到各个单元之间的水量平衡。
4 结果与分析
模型采用天津市气象局提供的以北京时间为准的2009—2015年10次降雨资料进行模拟。
4.1 模型调试
暴雨造成的内涝灾害可以用积水深度和积水时间来验证。模型采用调试参数的依据有示范段特征点积水深度、河道液位。模型首先采用10次降雨中过程比较典型的2012-07-25T8:00—26T13:00时的降雨过程作为模型调试的参考数据。
模型实测数据采用湘江道津河液位数据以及降雨过程(2012-07-25T8:00—26T13:00)中验证点西南楼地区的实测积水深度,对模型进行调试,模拟结果与实测数据对比如表1所示,相应的积水过程如图5所示。
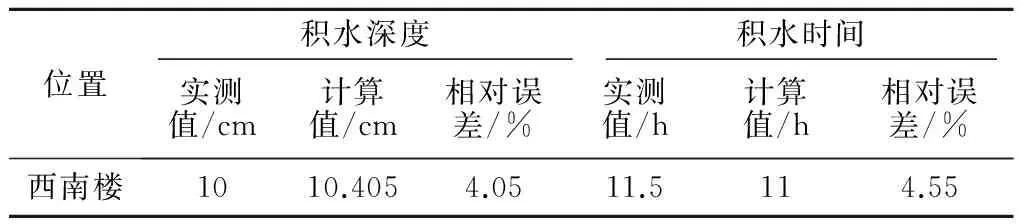
表1 积水深度和积水时间比较
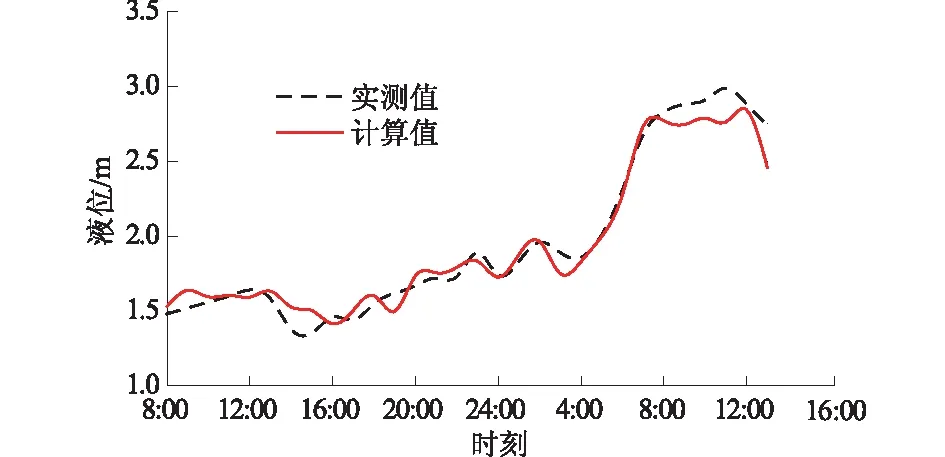
图5 积水过程模拟Fig.5 Process of waterlogging
由计算结果可以看出,积水深度和积水时间的计算值与实测值存在一定的误差,相比于模型参数率定的复杂性(泵站的收水运行规则、闸门的启闭过程等),误差均在可接受范围之内,液位的变化实测值和模拟值在整个积水过程都有很好的拟合度。因此模型具有较高的可信度。
4.2 模型验证
根据降雨过程2012-07-25T8:00—26T13:00调试好的模型对9个降雨过程进行模拟,由于验证点的积水水深及历时资料并不完备,并不能与9次降雨完全匹配,所以选取水量平衡的方法进行模型验证。
4.2.1 湘江道液位模拟结果
模型采用分区分层、立体多重的模式进行计算,雨水径流最终汇集到湘江道附近的河流液位,可以将液位变化作为模型调试的一个依据。为了更直观地显示对比结果,作平均水位的对比结果表(见表2);另外9次降雨过程液位实测值与模拟值对比结果如图6。
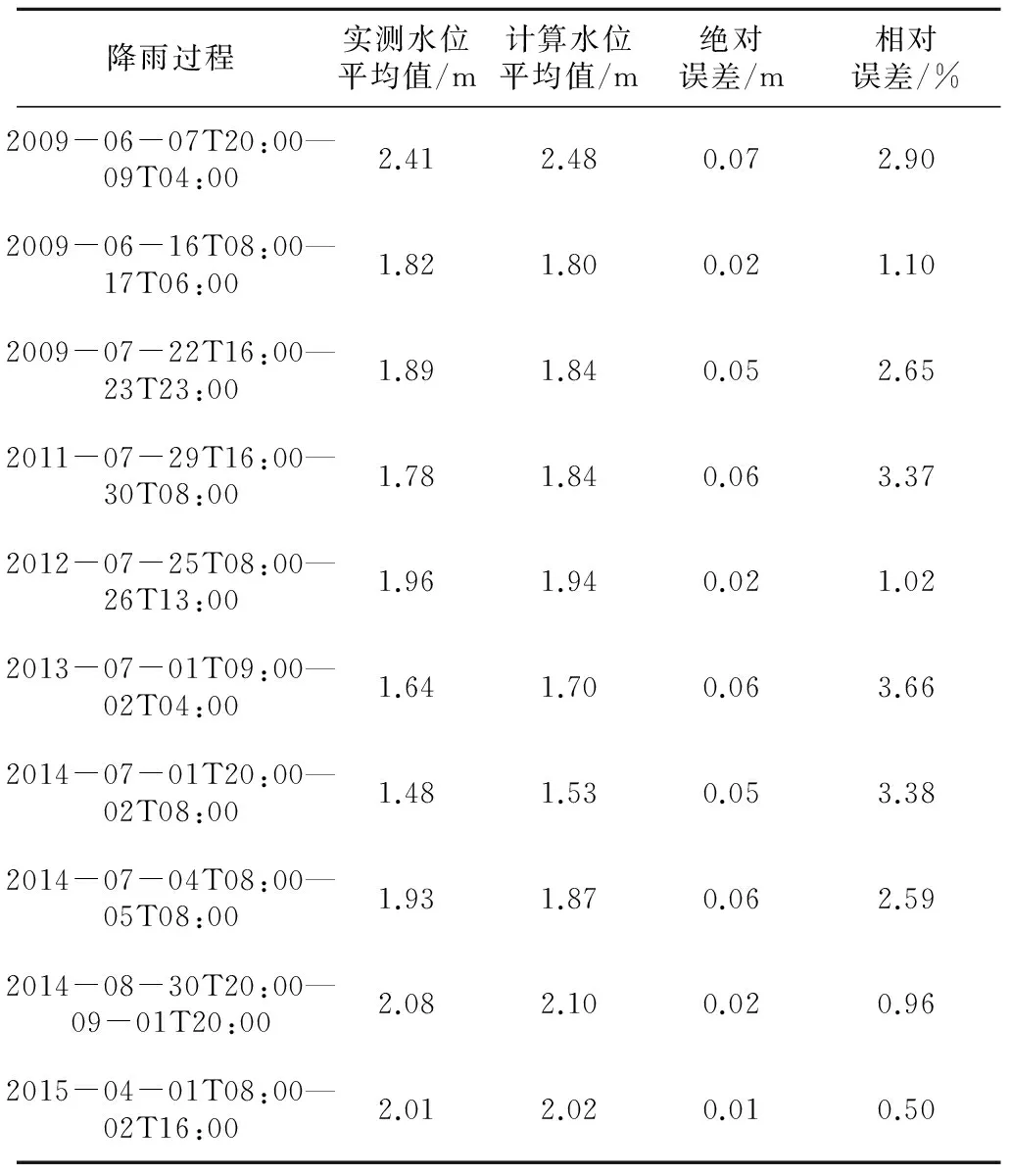
表2 模拟的河道平均水位与实况平均水位对比
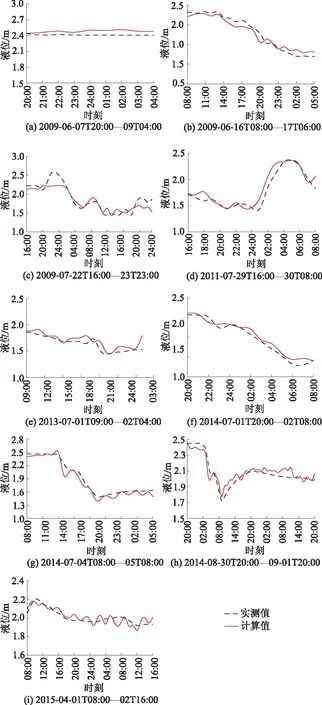
图6 9次降雨过程湘江道液位对比Fig.6 Comparison of liquid level near Xiangjiang road in 9 times of rainfal
从模拟的结果可以看出:9次湘江道液位模拟值的变化要早于实测值,但二者发生变化的时间点相差不多,二者得出的液位变化趋势一致。在降雨初期,液位变化拟合较好的有图6中的(b),(e),(f),(g),(h)过程;在降雨末期,实测液位变化趋于平稳,模拟液位变化波动频繁,原因是湘江道液位数据采样频率较低以及降雨中后期人工排水措施导致的降雨汇流相对集中。平均水位对比结果中,水位相对误差>3%的降雨过程有3次,在模拟误差可接受的范围之内,模型的精度达到标准。
4.2.2 水量平衡的模拟结果
模型液位变化保持一致并不能保证模型在水量上不会引起偏差,在此基础上对10次降雨的总降雨量和总蓄水量进行了水量平衡的计算,计算结果见表3(注:总降雨量=总蓄水量+河网排水量)。
由表3可知,10次降雨过程中降雨总量与雨水径流总量之间的偏差都趋近于0(相差值超过数值精度,近似为0),模型对于水量交换及水量平衡的模拟效果很好,进一步说明了模型精度达到了标准。
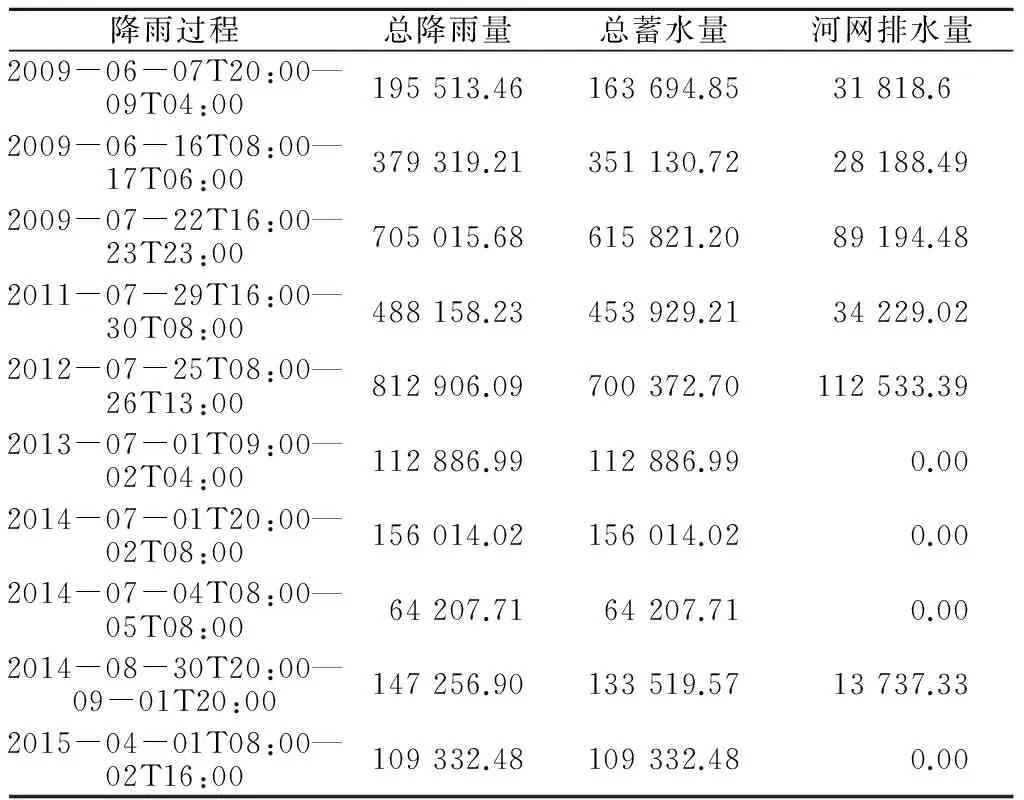
表3 水量平衡计算成果
5 结 论
本文建立的暴雨沥涝数学模型系统地模拟城市降雨、产流、汇流过程,不仅考虑到了降雨的时空分布不均情况,还对研究区域进行分区分层、立体多重化,更好地模拟了各个模块之间的水量交换,大大提高了模型计算精度。模型在缺乏积水水深和积水时间资料的情况下,采取降雨最终汇流位置河网的液位作为验证指标之一,液位的模拟结果与实测的变化趋势一致,平均液位的模拟结果精度也较高,相对误差<3%的过程有70%;同时从模型计算的水量平衡角度验证了模型计算的精确性,总体上,误差在可接受范围之内,为城市暴雨积涝模型研究提供了一个新的思路。
[1] 李 娜,仇劲卫,程晓陶,等.天津市城区暴雨沥涝仿真模拟系统的研究[J].自然灾害学报,2002,11(2):112-118.
[2] 芮孝芳,蒋成煜,陈清锦.论城市排水防涝工程水文问题[J].水利水电科技进展,2015,35(1):42-48.
[3] 胡伟贤,何文华,黄国如,等.城市雨洪模拟技术研究进展[J].水科学进展,2010,21(1):137-144.
[4] 岑国平.城市雨水径流计算模型[J].水利学报,1990,(10):68-75.
[5] 岑国平,沈 晋,范荣生.城市暴雨径流计算模型的建立和检验[J].西安理工大学学报,1996,12(3):184-190,225.
[6] 岑国平.城市雨水径流计算方法研究[D].南京:河海大学,1989.
[7] 仲志余.城市雨水径流计算模型研究[D].南京:河海大学,1989.
[8] 周玉文,赵洪宾.城市雨水径流模型研究[J].中国给水排水,1997,13(4):4-6.
[9] 徐向阳.平原城市雨洪过程模拟[J].水利学报,1998,(8):34-37.
[10]张景国.雨水地面径流模拟的一种方法——运动流理论及其应用[J].环境工程,1994,12(2):58-61.
[11]芩国平.雨水管网的动力波模拟及试验验证[J].给水排水,1995,(10):11-13.
[12]LI Da-ming, ZHANG Hong-ping, Li Bing-fei,etal. Basic Theory and Mathematical Modeling of Urban Rainstorm Water Logging[J]. Journal of Hydrodynamics, 2004, 16(1):17-27.
[13]解以扬,李大鸣,李培彦,等.城市暴雨内涝数学模型的研究与应用[J].水科学进展,2005,16(3):384-390.
[14]解以扬,李大鸣, 沈树勤,等. “030704”南京市特大暴雨内涝灾害的仿真模拟[J]. 长江科学院院报, 2004,21(6): 73-76.
(编辑:姜小兰)
A Mathematical Modeling of Urban Rainstorm Water Logging:Research and Application
LI Da-ming, HU Yong-wen, WANG Xiao, FAN Li-hong
(State key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China)
To solve the problem of urban rainstorm water logging, a partitioned and stratified calculation pattern is used in the model which is established on the basis of two-dimensional unsteady flow theory and finite volume method improved by hydrologic budget. In view of complicated city water runoff, the model mainly simulates urban community, street, network of drains and river flow. Data of 10 rainfalls from 2009 to 2015 in the demonstration area of Tianjin is used in the model to analyze and compare the water levels of verification points and Jinhe river. Results show that both of the average values differ less than 10 cm, indicating that the model is of precision and can be applied to forecasting urban water logging. It provides a new method and idea for the mathematical modeling of urban rainstorm waterlogging.
rainstorm waterlogging; hydrologic budget; finite volume method; partition and stratification; urban waterlogging
2015-08-31;
2015-11-24
李大鸣(1957 - )男,河北枣强人,教授,博士,主要从事水力学及河流动力学方面的研究,(电话)022-87401579(电子信箱)lidaming@tju.edu.cn。
10.11988/ckyyb.20150728
2016,33(10):46-50
TV125
A
1001-5485(2016)10-0046-05
