采煤机整机力学模型的预条件拟极小剩余算法

刘春生， 李孝宇

(1.黑龙江科技大学， 哈尔滨 150022； 2.黑龙江科技大学 机械工程学院， 哈尔滨 150022)



采煤机整机力学模型的预条件拟极小剩余算法

刘春生1， 李孝宇2

(1.黑龙江科技大学， 哈尔滨 150022； 2.黑龙江科技大学 机械工程学院， 哈尔滨 150022)

为了得到不同工况下采煤机各个滑靴的受力状态及其运动特性，在考虑仰俯角和煤层倾角的条件下，建立了采煤机整机力学模型。采用Krylov子空间方法的拟极小剩余法，解算出不同工况下各滑靴受力的最佳逼近值，分析随着煤层倾角和仰俯角的变化采煤机各滑靴受力的变化规律。结果表明：行走轮前一轮齿退出啮合、后一轮齿进入啮合时与销齿啮合区由圆弧段过渡到斜线段时，加速度值会出现两次突变；后导向滑靴受正压力较大，煤层倾角对各滑靴的受力状态影响相对较小。该研究为采煤机整机力学特性的分析提供了参考。

采煤机； 整机力学模型； 拟极小剩余法； 惯性力

0 引 言

采煤机是煤炭生产中主要的机械设备之一。随着大功率、大采高采煤机的发展，整机装机功率的增大，导向滑靴承受的负载力也越来越大，导致采煤机牵引部的一些关键部件因过载而损坏、失效如行走轮非正常断齿、导向滑靴非正常损坏，以及行走轮和销排销齿的异常磨损等问题频繁出现。诸多学者对采煤机行走轮动力学特性，陈伟等[1]利用Pro/E进行摆线行走轮的实体建模，通过ANSYS进行受力分析，证明了MG750/1815-WD采煤机摆线行走轮满足强度。王振乾等[2]给出了行走轮五种齿形的强度和适应性。由于采煤机整机受力的复杂性，很难确定采煤机关键承载部件的参数。刘春生等[3]采用最小二乘解算方法对采煤机的力学模型进行解算，求解出采煤机实际工作过程中各个滑靴的力情况。采煤机在行走过程中，由于行走轮齿轮轮廓与销排销齿齿廓不能形成共轭啮合，行走传动比时刻发生变化，引起采煤机的速度和加速度变化，产生采煤机行走附加惯性力。笔者考虑附加惯性力的影响，建立采煤机整机力学模型，利用QMR算法求解非对称大型稀疏线性系统的计算和存储量均比较小的优势对采煤机整机力学模型进行求解，以期为分析采煤机的力学特性提供参考。

1 整机力学模型

在具有一定的仰俯角和煤层倾角的条件下，建立三维直角坐标系，如图1所示，分析采煤机的力学状态。

图1 采煤机受力分析

由图1可见，沿x、y、z三个坐标轴方向分别列出力平衡方程，ΣFx=0，ΣFy=0，ΣFz=0；以采煤机中心O点列三个力矩平衡方程，ΣFxoy=0，ΣFxoz=

0，ΣFyoz=0，即

(1)

式中：a1=-F1-F2-Gcosαsinβ；

a2=(2T+2FG-Gsinα-Fz1-Fz2)/μ；

a3=Gcosαsinβ-2F-FJ1+FJ2；

a4=-2Th0-2FG-FJ1(lcosθ1+l1+l0/2)-fz1(lsinθ1+h1-h0)-FJ2(lcosθ2+

l1+l0/2)+Fz2(lsinθ2+h0-h1);

a5=2Fb2+FJ2(b0+b1)-FJ1(b0+b1)-F1(lsinθ1+h1-h0)+F2(lsinθ2+h0-h1);

a6=-2Tb2-2FGb2-(Fz1+Fz2)(b0+b1)+

F1(lcosθ1+l1+l0/2+e)-F2(lcosθ2+

l1+l0/2+e);

T——单个牵引机构牵引力，kN；

F——单个牵引机构的垂直分力，kN；

μ——导向滑靴与导轨的摩擦系数，μ=0.18；

γ——行走轮与销齿的啮合角，(°)；

G——采煤机的整机重，kN；

θ1、θ2——前后截割部的几何摆角，(°)；

Ni——前、后支撑和导向滑靴所受支撑力，(i=1,z,…,6)，kN；

FJ1、FJ2——前、后螺旋滚筒截割阻力，kN；

Fz1、Fz2——前、后螺旋滚筒推进阻力，kN；

F1、F2——前、后螺旋滚筒轴向力，kN；

α、β——分别为煤层倾角和仰俯角，(°)；

li、bi、hi——各受力点的主要位置尺寸，mm；

e——轴向力作用位置距螺旋滚筒轴线的偏距，mm；

FG——采煤机行走附加惯性力,kN；

令C41=l0/2-μ(h0+h2)，C42=l0/2-μ(h0+h2)，C43=-μh0±l0/2，C44=-l0/2-μh0，C45=-μh0，C61=-μb1，C63=-μb2，C65=-μ(b3+b2)-l0/2，C66=-μ(b2-b3)-l0/2。

将式(1)写成矩阵的形式：

(2)

即

UX=A。

(3)

对式(3)首先判断其解的存在情况，即独立方程的个数。实际生产实践中，N3的方向具有不确定性，当N3向上时取上行符号，当N3向下时取下行符号。分别对两种情况的系数矩阵U作初等变换，当N3的方向向上是，U的秩是5；当N3的方向下时U的秩是6。N3方向的不确定性直接影响了系数矩阵U的秩。

2 外部载荷的确定

2.1 螺旋滚筒截割的确定

根据文献[4]前螺旋滚筒(截割阻力FJ1，推进阻力Fz1和轴向力F1)可按式(4)进行计算，后螺旋滚筒的按照前螺旋滚筒乘以工作条件系数k1，取k1=0.8。

(4)

式中：PH——单截割电机额定功率，kW；

DC——螺旋滚筒直接，mm；

ηj——截割部的传动效率，ηj=0.85；

J——螺旋滚筒有效截深，m；

n——螺旋滚筒转速，r/min;

Lk——螺旋滚筒端盘部分截齿的截割宽度，m，取Lk=0.2 m；

kq——截割磨损程度系数，取kq=0.6～0.8；

k2——螺旋滚筒端盘部分接近半封闭截割条件的系数，取k2=2。

2.2 附加惯性力的确定

2.2.1 行走轮与销齿轮廓线方程

采煤机在行走过程中，由于行走轮与销齿在啮合时不共轭，会产生惯性力。文中研究的采煤机行走轮齿廓为摆线轮。摆线齿廓的行走轮，一般由齿顶处的外摆线和齿根处的内摆线两部分组成，见2所示。

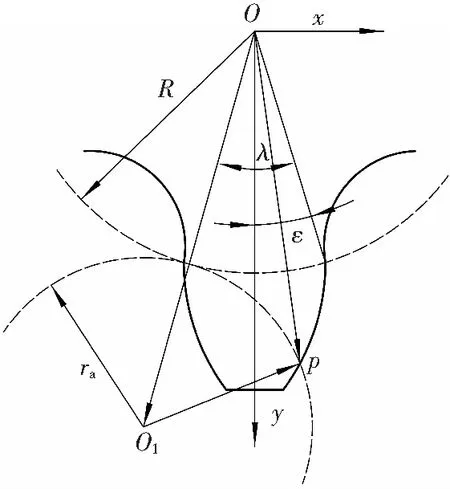
a 外摆线

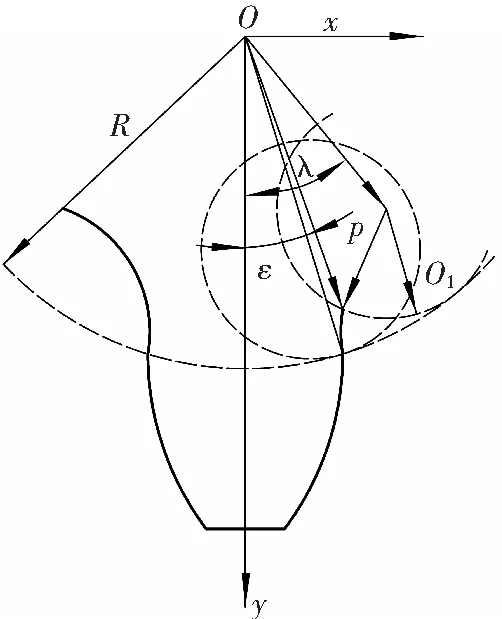
b 内摆线

(1)外摆线齿廓线方程

由图2可见，一个动圆外切与一个定圆作无滑动的纯滚动，动圆圆周上一个定点的轨迹称为普通外摆线，定圆称为基圆，如图2所示，外摆线的矢量-矩阵方程[5]为

OP=OO1+O1P,

即：

r1(λ)=(R+ra)Kτ1j-raKτ2j。

(5)

直角坐标系中的方程为

式中：R——采煤机行走轮节圆半径，mm；

ra——外摆线外滚圆半径，mm；

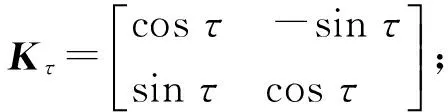
τ1——旋转角，τ1=λ-ε,(°);

λ——滚圆圆心和节圆圆心连线与起始线的夹角，(°)；

ε——行走轮节圆弦齿夹角的一半，(°)。

(2) 内摆线齿廓线方程

动圆内切与一个定圆作无滑动的纯滚动时，动圆上一个定点形成的轨迹成为普通内摆线。如图2所示。普通内摆线的矢量-矩阵方程为

OP=OO1+O1P，

即

r1(λ)=(R-rf)Kτ3j+rfKτ4j。

(6)

直角坐标系中的方程为

式中：rf——内摆线内滚圆半径，mm;

τ3——旋转角，τ3=-λ-ε，(°)；

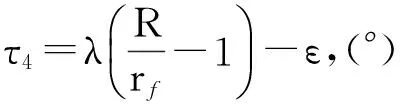
(3) 销齿齿廓线方程

文中与行走轮配套的销齿是截距为147mm的大截距销齿。其齿廓线上面部分采用半径为80mm的圆弧曲线，下面部分采用圆角曲线，中间用相切的直线过渡。上面圆弧段和过渡斜线段是主要的啮合区。代入实际的相关尺寸后，啮合区的矢量—矩阵方程圆弧段为

r2(μ)=Kμri，

(7)

斜线段为

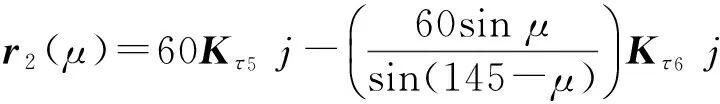
(8)

式中：μ——啮合过程中销齿滚动过的相对角度;

τ5——旋转角，τ1=40°；

τ6——旋转角，τ1=15°。

2.2.2 行走轮与销齿的啮合传动比

采煤机实际行走过程中，销排固定在地面上，行走轮一边转动一边前进。在不改变此实际相对运动关系的条件下，假设行走轮作定轴转动，销排做平移运动。行走轮转过ψ角度，原直角坐标oxy变为ox1y1,销排所在坐标系o2x2y2向前平移了S(ψ)，如图3所示。根据齿轮啮合原理的接触条件和相切条件，行走轮轮齿与销齿的啮合方程为：

(9)

式中：ψ——行走轮转过的角度，(°)；

B——行走轮与销齿啮合中心距，mm。

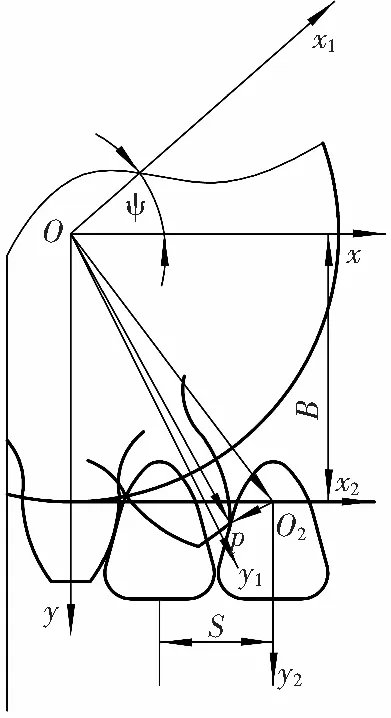
图3 行走轮与销齿啮合矢量

Fig. 3 Vector of meshing between traveling wheel and pin

对行走轮与销齿的啮合方程两边对ψ求导，整理化简后，得到行走轮与销齿圆弧段啮合的传动比：

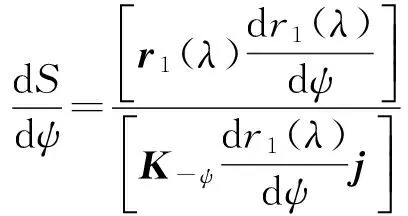
(10)

行走轮与销齿的斜线段啮合的传动比为

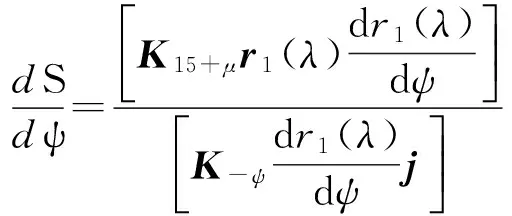
(11)

将式(5)、(7)带入式(10)，整理可得到内、外摆线与圆形齿廓啮合传动比，内摆线为

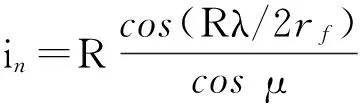
外摆线为

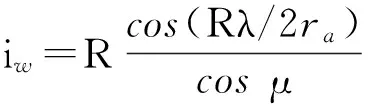
将式(5)和(8)带入式(11)，简化整理，可得外摆线与斜线段啮合传动比：

斜线段

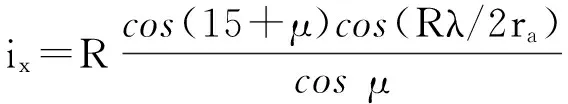
根据传动比即可求解采煤机行走速度以及加速度，进而求解采煤机行走附加惯性力。

v=iω,

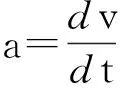
FG=ma，

式中：ω——行走轮角速度，rad/s；

v——采煤机行走速度，mm/s；

a——采煤机行走加速度，mm/s2；

m——采煤机质量，kg。

2.3 牵引力的确定

根据文献[3]，牵引力可按式(17)进行计算：

T=[μ(Gcosα-FJ1+FJ2+F1+F2)+FZ1+

Fz2+Gsinα-FG]k3。

(17)

式中：k3——安全系数，k3=1.20～1.25。

3 解算方法

3.1 拟极小剩余法

采煤机受力力学模型的系数矩阵为奇异阵，因此方程无精确的解[6-10]，但是采用Krylov子空间方法中拟极小剩余法(QMR)可以在求解某预条件下的近似解X。

QMR算法是Krylov子空间迭代法。令x0为初始向量，r0为初始残差，令Kk(A,r0)为k次krylov子空间，即，Kk(A,r0)=span{r0,Ar0，…，Ak-1r0}，构造迭代序列{xk}，使xk∈x0+Kk(A,r0)，令β=‖r0‖2，v1=r0/β，取w1=v1，由Lanczos算法可得Lanczos向量v1,v2,…,vk，则

xk=x0+[v1,v2,…,vk]zk=x0+Vkzk,zk∈k,

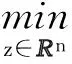
对于线性方程组

AX=B，

(13)

当矩阵A是奇异矩阵式，A-1是不存在的，故选用一个奇异矩阵M作为奇异线性系统的预条件阵可能更合理。设M是奇异的，求解线性系统AX=B可以通过求解下面的预条件方程：

M+Ax=M+B,

3.2 模型的计算

采煤机力学模型的计算需要对式(3)增广矩阵进行初等变换，首先考虑到N3的受力方向，当N3受力向下时，系数矩阵U的秩是6，通过正常求解方式即可求解。当N3方向向上是，系数矩阵U的秩为5，根据上述理论对奇异线性方程组UX=A进行求解。

首先求解两个初等变换阵P和Q，它们分别交换矩阵U的第ik和k行以及第jk和k列，k=1,2,…，r。即

W11=W(i1,i2,…,ir;j1,j2,…,jr)是秩为5的W的子式，然后根据下面式子求解U+

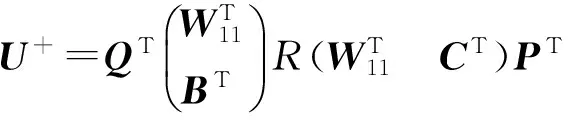
4 算例与结果分析

以某厚煤层采煤机为例，计算不同仰俯角和煤层倾角的工况下，支撑于导向滑靴的受力情况。基本性能参数为：机重约1 460kN，最大牵引力1 391kN，单截割电机功率1 000kW，螺旋滚筒转速25.66r/min，螺旋滚筒直径3.2mm，截深865mm，采煤机主要技术参数和位置尺寸，见表1。

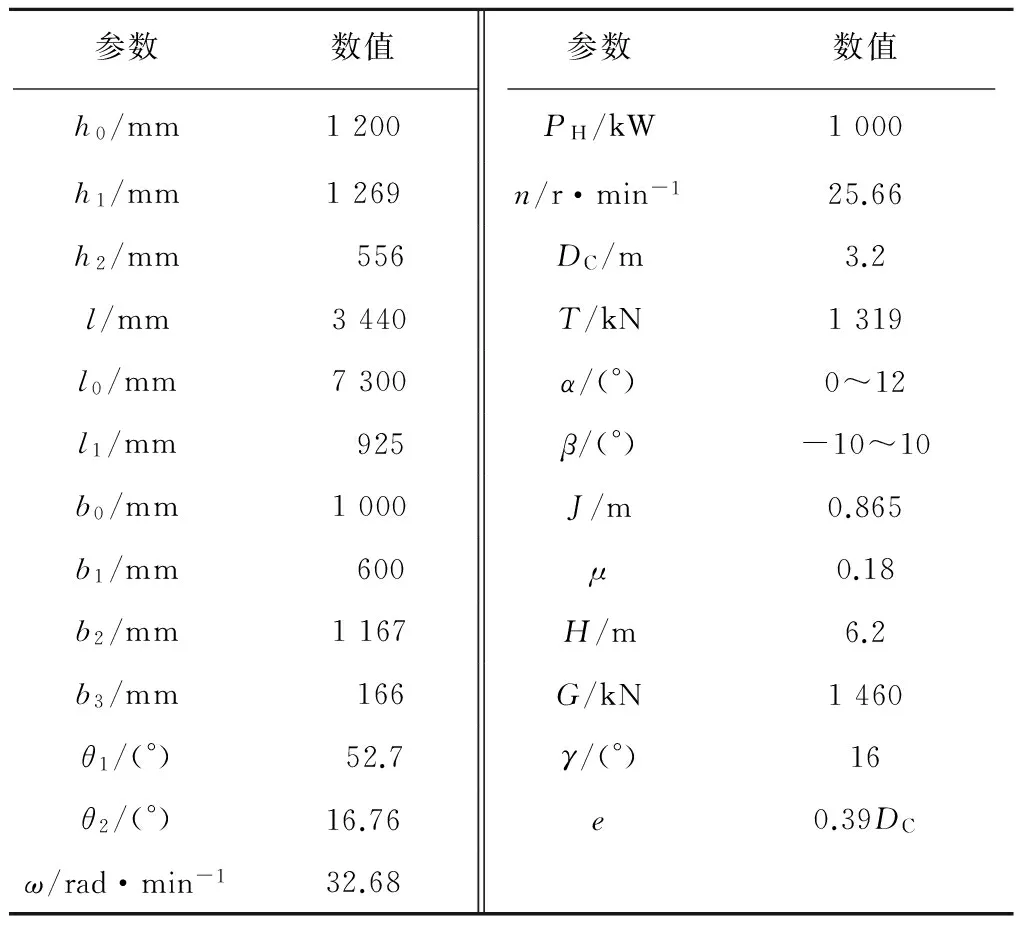
表1 整机技术参数

根据整机技术参数，通过式(4)计算采煤机前螺旋滚筒截割阻力FJ1为197.72 kN，推进阻力Fz1为158.17 kN和轴向力F1为91.43 kN，后螺旋滚筒的截割阻力FJ2为158.17 kN，推进阻力Fz1为126.53 kN和轴向力F1为73.14 kN。通过式(17)计算采煤机牵引力为572.14 kN。根据式(14)和(15)计算采煤机行走速度和加速度，如图4所示。

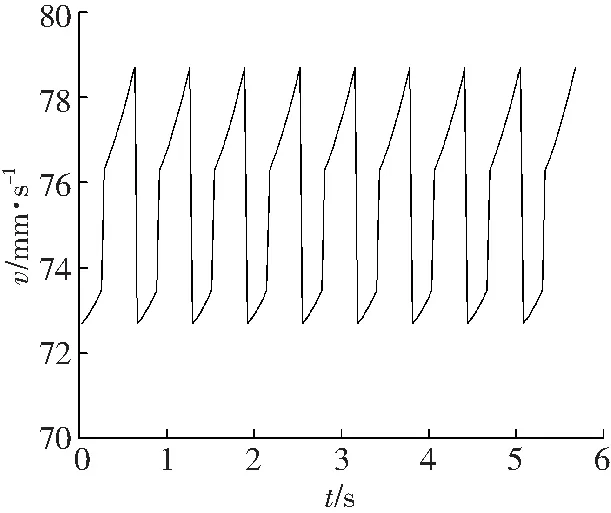
a 速度

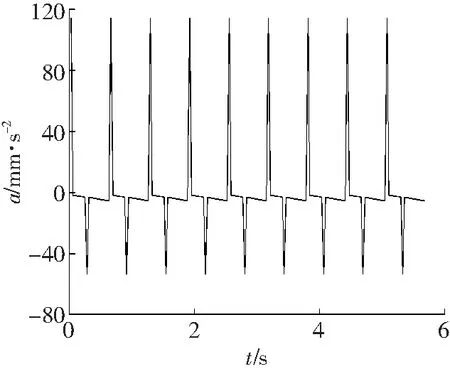
b 加速度

摆线行走轮与啮齿啮合过程中，行走轮内摆线部分基本不参与啮合，行走轮的主要啮合区为外摆线部分。从图4中可以看出，采煤机行走速度在74 mm/s处上下波动，速度的变化主要分为两个阶段：外摆线与销齿圆弧段啮合和外摆线与销齿斜线段啮合。这两个阶段速度的变化都呈递减趋势，外摆线与圆弧段啮合到外摆线与斜线段啮合的过渡区域速度发生突变。加速度变化曲线中出现两个峰值，分别为114.07和-53.25 mm/s2，其中加速度最大值114.07 mm/s2出现在行走轮的前一个齿退出啮合，后一个齿进入啮合的时刻；加速度第二峰值-53.25 mm/s2出现在销齿啮合区由圆弧段到斜线段过渡的时刻。

各滑靴所受变化如图5所示，从图5中可以看出，仰俯角β从-10°～10°变化，N3、N4、N6均有明显增加其余滑靴受力均呈递减趋势， 当α=0°时，大约在β=6°处，N5的受力方向发生改变。当煤层倾角α由0°～14°变化，N3有略微下降，N4的值基本保持不变，其余滑靴受力均呈递增趋势。当β=6°时，大约α=10° 处，N5的受力方向发生改变。

a 实线α=14°,虚线α=0°

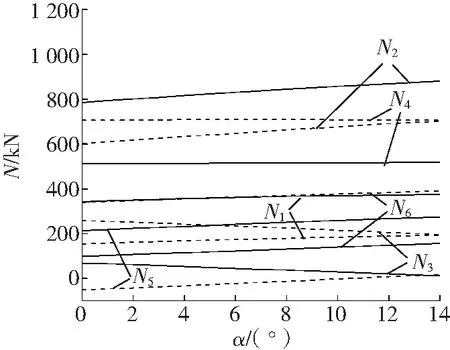
b 实线β=10°,虚线β=10°

5 结 论

(1)对采煤机整机力学模型进行分析时，考虑了采煤机行走过程中，行走轮与销齿啮合时不共轭产生的附加惯性力，采用Krylov子空间方法拟极小剩余法(QMR)对采煤机整机受力模型进行解算，通过迭代方法减小残差，解出各滑靴受力的最佳逼近值。

(2)行走轮与销齿啮合过程中，速度与加速度有两个突变点，第一个突变点发生在前一个轮齿脱出啮合下一个轮齿进入啮合的时刻；第二个突变发生在销齿的啮合区由圆弧段过渡到斜线段的时刻。

(3)随着仰俯角和煤层倾角由小到大，各个支撑反力基本呈线性变化，变化趋势受仰俯角的影响比较大。其中，N1和N2随着仰俯角的增大而减小；N3、N4和N6随着仰俯角的增大而增大；N5随着仰俯角的增大先减小后增大。随着煤层倾角的增大，N3呈递减趋势，其余滑靴的受力均呈递增状态。

(4)N4受煤层倾角影响较小，其数值基本保持不变；N2数值较大，说明后支撑滑靴受力正压力较大，磨损严重；随着仰俯角的增大，N5先减小后增大，大约在β=6°时，受力方向发生改变，由原来滑靴与导轨的正压力变为滑靴下勾处于导轨的拉力，这种受力方式对于滑靴非常不利，严重影响滑靴的使用寿命。

(5)各滑靴的载荷受采煤机仰俯角影响较大。

[1] 陈 伟, 杜长龙, 夏丽建, 等. 采煤机行走机构摆线轮设计研究[J]. 煤矿机械, 2010(1): 1-2.

[2] 王振乾, 周常飞. 采煤机用行走轮的几种齿形曲线初探[J]. 机械设计与研究, 2011(7): 39-42

[3] 刘春生, 田 操. 采煤机整机力学模型的最小二乘解算方法[J]. 辽宁工程技术大学学报： 自然科学版, 2015, 34(4): 505-509.[4] 刘春生, 戴淑芝. 双滚筒式采煤机整机力学模型与解算方法[J]. 黑龙江科技学院学报, 2012， 22(1): 33-38.

[5] 王振乾. 滚筒式采煤机行走机构运动学分级及强度研究[D]. 上海: 煤炭科学研究总院上海分院, 2007.

[6] 张世洪. 我国综采采煤机技术的创新研究[J]. 煤炭学报, 2010, 11(5): 1898-1902.

[7] 吴佳梁, 尹 力, 李 勇, 等. 智能化联合采煤系统及其关键技术[J]. 辽宁工程技术大学学报: 自然科学版, 2014, 33(2): 226-231.

[8] 刘春生, 李德根. 不同截割状态下镐型截齿侧向力的实验与理论模型[J]. 煤炭学报, 2016, 41(9): 2359-2366.

[9] 李庆茹, 申 磊, 李玉标. 新型采煤机行走轮的研究与探讨[J]. 煤矿机械, 2011, 32(12): 158-159.

[10] 张勇涛, 王兴文, 李 英, 等. 采煤机行走部导向滑靴分析[J]. 煤矿机械, 2012, 33(11): 210-211

[11] 郎国军, 苑雪涛, 庹文敏, 等. 采煤机行走轮断齿现象分析[J]. 煤矿机电, 2010(3): 34-35.

(编校 李德根)

Shearer mechanics model preconditioned quasi-minimal residual algorithm

LiuChunsheng1,LiXiaoyu2

(1.Heilongjiang University Science & Technology, Harbin 150022, China;2.School of Mechanical Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

This paper is concerned with a better insight into the stress state of shearer and the motion characteristics of shearer under different working conditions; and the development of the mechanics model of shearer, along with the consideration of the conditions of the elevation angle and the inclination of coal seam. The research involves using Krylov subspace method of quasi minimal residual method, calculating the optimal approximation of slippers under force values due to different conditions, and delving into the mechanism by which the slippers are subjected to varying forces, depending on the variation of coal seam angle and pitch angle of the machine. Results show that there occur two sudden changes in the acceleration value when the engagement area of the pin tooth moves from the arc section to the oblique line segment, the front of the running gear is engaged with the gear wheel, and the rear gear tooth enters the engagement time. Rear guide sliding boots are subjected to a greater positive pressure and coal seam dip angle has a relatively small effect on the stress state of each shoe. This study might provide a reference for the analysis of mechanical properties of coal mining machines.

coal winning machine; force of the whole machine; quasi-minimal residual method; inertial force

2016-08-26

国家自然科学基金项目(51274091)；黑龙江省教育厅科学技术研究项目(12531006)

刘春生(1961-)，男，山东省牟平人，教授，研究方向:机械设计和液压传动与控制，E-mail:liu_chunsheng@163.com。

10.3969/j.issn.2095-7262.2016.05.017

TD421.61

2095-7262(2016)05-0552-06

A