从高考试题看数学素养培养之必要
——浪漫的古代文化情结
2016-12-09宫琼
宫 琼
(西安惠安中学 西安惠安 362100)
从高考试题看数学素养培养之必要
——浪漫的古代文化情结
宫 琼
(西安惠安中学 西安惠安 362100)
在新一轮课改中,高中课程标准提出了各学科的“核心素养”,其中,明确指出要能够“理解数学的科学价值、应用价值、文化价值,形成批判性思维习惯、理性精神”。在今后高考数学的新考纲中也明确提出增加考点“数学文化”。在高考这根指挥棒下,一些普及数学名著的高考试题已经应运而生,本文对部分高考试题进行整理,只是希望能够引起更多的人关注,让数学文化走进课堂,使数学的精神、思想和方法深深地铭刻于学生的头脑之中,使学生数学素养得以提升,终生受益。
高中数学 数学文化 数学素养
何为“阳马”、“鳖臑”?在2015年的高考过后,这两词迅速引起广泛议论。有人说: “这道题不好,因为大多数人不知道阳马为何物,鳖臑该怎么读。在数学这样一个考场中,最终要考的是数学能力,而不是语言基础,数学没必要来越俎代庖。”也有人说:“如果一个人不知道《三国演义》、《水浒传》和《红楼梦》等文学名著,会被认为文化素养不高,但是一个人不知道《九章算术》、《数书九章》等数学名著,却不被看作缺少文化。”上面的说法,其实都涉及到一个问题,就是数学文化。
所谓“数学文化”,狭义指:数学的思想、精神、方法、观点、语言,以及它们的形成和发展。广义上除上述内涵以外,还包含数学家,数学史,数学美,数学教育等等。然而,由于长期受应试教育的影响,我们的数学教育依然存在着某些误区:数学课程过分强调它的“逻辑性”、“演绎性”、“封闭性”;课堂教学中,解题教学占据了主导地位,通过大量练习来学习数学,是当今我国数学教学的主旋律。通过大量模仿性练习,这对提高学生基本运算能力、逻辑推演能力和解题能力的确有效,但他们无法体会到数学的文化价值,更缺乏创新精神,数学素养的缺失,不能不说是数学教育的一个严重的缺陷。
可喜的是,数学文化经过高考这根指挥棒,引起更多的人关注,真是一件幸事。一些普及数学名著的高考试题应运而生,数学名著因这些高考试题而渐入高中数学课堂,这些试题也因普及数学名著而成为经典试题。细数高考历年数学试题,竟然有不少试题背景是我国古代数学文化,举例如下:
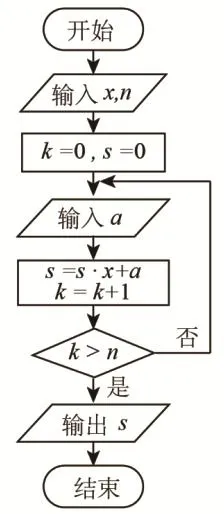
题目1:(2016全国Ⅱ)中国古代有计算多项式值的秦九韶算法,上图是实现该算法的程序框图.执行该程序框图,若输入的依次输入的a为2,2,5,则输出的s=( C )
(A)7
(B)12
(C)17
(D)34
分析:本题是程序框图题,以古代的“秦九韶算法”为素材,目的在于考查学生对程序框图的认识和理解及运算求解能力。
题目2:(2015全国Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有 ( )
A.14斛 B.22斛 C.36斛 D.66斛
分析:本题是以我国古代数学名著《九章算术》为背景,实际上考查了圆锥的体积计算及考生的理解和计算能力。
题目3:(2015湖北)我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534 石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
A.134石 B.169石
C.338石 D.1365石
分析:本题以《数书九章》中的“米谷粒分”为背景,主要考查用样本估计总体,目的在于考查考生运用数学知识解决实际问题的能力。
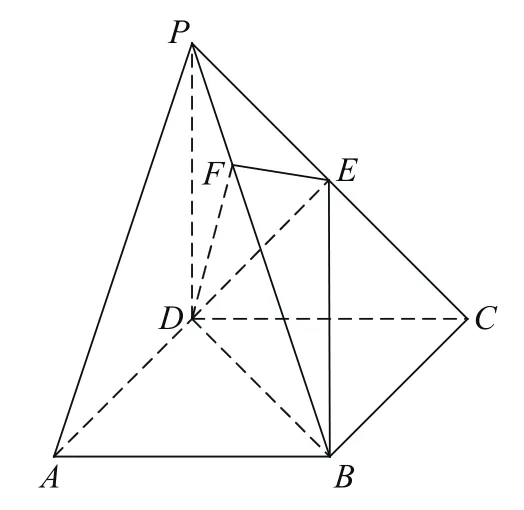
题目4:(2015湖北)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马P−ABCD中,侧棱PD⊥底面ABCD,且PD=CD,过棱PC的中点E,作EF⊥PB交PB于点F,连接(Ⅰ)证明:平 面试判断四面体DBEF是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(Ⅱ)若面DEF与面ABCD所成二面角的大小为,求的值。
分析:本题以《九章算术·商功》中两个特殊锥体——阳马、鳖臑为背景,主要考查数学史中的立体几何问题,四棱锥的性质,线、面垂直的性质与判定、二面角。目的在于考查学生的分析转化能力、推理论证能力、空间想象能力。
我国数学文化历史悠久,有着鲜明特点,注重归纳、强调实用、讲究算法。如古代数学名著《九章算术》,全书采用问题集的形式,收有246个与生产、生活实践有联系的应用问题。它成书于东汉,是当时世界上最先进的应用数学著作,它采用十进位值制记数法,马克思称颂十进位值制记数法是“人类最美妙的发明之一”。
除了上面列举的四道题,高考试题中的以数学文化为背景的试题还有很多,特别是湖北省自2010年以来,几乎每年都有一题,背景涉及古今中外,视角触及天边眼前,蕴含着浓郁的文化意韵,流淌着鲜活的数学思想。
纵观这些试题,构思精巧、内涵丰富,以别具一格的“气质”装点着高考数学卷。从难度上看,均属于容易题和中等难度题。在解答时,首先要求学生能阅读并理解所提供的信息资料,其次在试题营造出来的氛围中发现问题、解决问题,感受数学的思维方式,体验数学的理性精神,用数学的观点认识世界、观察社会、思考问题。
其实,这些试题的意义和价值,已远远超出高考本身。借助高考平台,让考生潜移默化地接受我国古代数学文化的熏陶,自觉形成严谨、务实的治学态度,传承中华优秀传统文化,弘扬爱国主义精神。最后,希望能够让数学文化走进课堂,使数学的精神、思想和方法深深地铭刻于学生的头脑之中,使他们终生受益。
