一种改进的非参数方法对金融价值风险的估计

张淑娟

（1.天津财经大学理工学院，天津300222；2.天津财经大学珠江学院，天津301811）

一种改进的非参数方法对金融价值风险的估计

张淑娟1,2

（1.天津财经大学理工学院，天津300222；2.天津财经大学珠江学院，天津301811）

文章对利用波动率计算价值风险VaR的方法进行了改进，提出了非参数波动率结合非参数条件核密度条件分位数方法来计算VaR，此非参数方法克服了模型误设的问题，不受波动率模型具体形式的限制，不受新息项分布函数的限制，是一种稳健的适应性方法。同时将此方法应用到中小板综指与创业版指进行实证分析，与相应的半参数及参数方法进行比较，发现文中提出的方法在某种程度上比较稳定可靠。

非参数分位数；非参数方差；价值风险

0　引言

伴随着经济全球化和金融市场一体化，金融市场变得越来越复杂，不确定性和风险也伴随而来，为了尽量降低风险带来的损失，金融机构和监管部门提出各种方法来对风险进行预测和控制。在不断的研究探索中，关于金融风险的度量理论和方法得到了极大的丰富和发展，度量工具VaR就是在这样的过程中建立并完善的，目前已成为风险控制行业的度量标准。

关于VaR的研究，国内外已有诸多学者进行了深入的探讨，估计方法主要有局部估值法与完全估值法，方差-协方差方法属于局部估值法的一种。在使用方差方法估计VaR时有两方面的问题：一是如何刻画金融数据的尖峰厚尾、波动簇集的时变特征，二是如何寻找金融数据的分布密度函数。自从engle[1](1982)、bolleslev[2](1986)分别提出ARCH与GARCH模型来描述金融市场的波动率，金融波动理论得到了极大的发展，比如EGARCH，GARCH-M，TGARCH等模型的建立。近年来国内外提出假设金融收益率服从某种固定分布，利用GARCH类模型结合新息项分布函数的分位数来计算VaR的参数方法[3-6]。但是在实际的金融市场中，尤其是像我国这样的金融市场的发展阶段，很难用固定的分布去准确的描述收益率的分布，所以在实际操作时比较容易产生误设的问题，因误设产生的误差是无法通过增加样本数量能够弥补的。针对参数模型的误设问题，本文提出了使用非参数可加GARCH模型来替代参数GARCH模型，非参数波动模型的设定不受模型固定形式的限制，更加灵活，同时可加非参数模型避免了非参数模型中的“维数灾难”问题；另一方面使用非参数条件密度函数的方法代替参数形式的分布函数，非参数条件分布方法完全由数据驱动，不受任何分布形式的限制，适用于任何复杂的平稳金融市场。最后通过失败率检验法，对非参数波动率结合非参数核密度分位数方法来计算VaR的结果，与参数GARCH模型结合参数分位数计算VaR结果进行对比发现，本文提出的非参数方法对VaR的估计在某种情况下具有更好的可靠性，同时具有很好的适应性，可以作为利用VaR进行风险管理的参考方法。

1　VaR估计与非参数核密度分位数、非参数波动模型

1.1VaR的定义、估计方法及检验

VaR就是“价值风险”，它是由J.P.Morgan公司首先提出的用来计算市场风险的产物，它与传统的度量风险手段不同，是完全基于统计分析基础上的风险度量技术。尽管VaR在很早的时候就被提出和使用，但是却一直没有一个严格的定义，Jorion把VaR定义为在有效的市场环境下与给定的时间段内及一定置信水平下，度量某种金融资产或投资组合的价值在未来某一段持有期内的预期最大损失值。从统计的角度，VaR可以看作收益率分布函数的分位数，数学形式可以表述为：

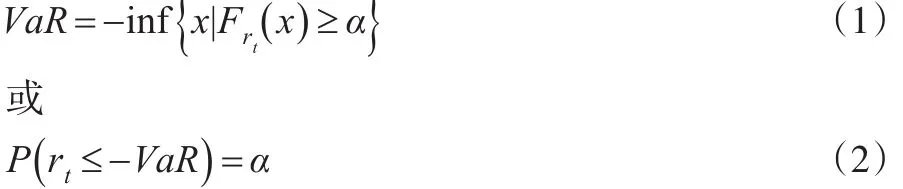
其中rt表示金融资产在t时刻的收益率，当rt是正值时表示收益，rt是负值时表示损失，风险测度关注的是随机变量rt左尾分布函数，用Frt(x)表示随机变量rt的分布函数，在置信水平1下，可以将VaR表示为式（1）或式（2）的形式。

令rt=ut+σtεt，则VaR的计算公式还可以用下式来表示：

式中Ωt为时间t的σ域，为预期收益率；σt为当期资产收益序列的波动率，式中关于新息项的分位数实质上就是分布函数的反函数，可以利用下式来计算：

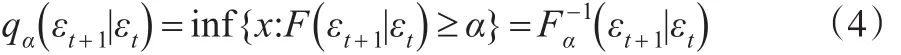
一个模型只有被证明预测的结果较为准为准确时，才有使用价值，因此需要对建立的模型进行检验，文中关于VaR的检验采用1995年Kupiec[7]提出的失败率检验法，也称Kupiec检验法，在置信水平1-α下，令实际共考察的天数为M，失败的天数共为N（实际损失超过VaR的值即称为失败），那么失败率可以记为，期望概率p*=1-α，零假设H0:p=p*，备择假设H1:p≠p*，检验失败率是否会服从零假设。建立的似然比方程为：

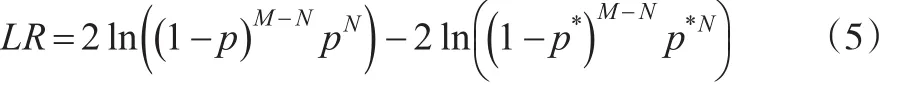
在零假设成立条件下，检验统计量LR则服从自由度为1的χ2分布，当LR越小时，P值会越大，则失败率会越接近α，模型就会越精确，可信度就越高。

由式（3）可知对VaR的估计需计算预期收益率、波动率及新息项的分位数，收益率采用常数收益率，下面分别来介绍波动率及新息项的分位数的相关内容。

1.2非参数核密度条件分位数

对比参数回归模型，非参数条件回归模型受约束少，同时对数据的分布不做要求，形式自由，完全由数据驱动，对非线性非齐次回归函数都有较好的估计效果，而非参数条件分布函数的估计本质上也是非参数条件回归函数的估计。利用设定参数分布函数的方法计算分位数，容易发生误设的问题，因此本文利用非参数方法来计算新息项的分布函数，进而计算出分位数。下面来介绍非参数条件分位回归及非参数条件分位数：

设Y是一维观测随机变量，X是m维观测随机变量，Y对X的条件回归函数为g(X)=E(Y|X)，令为一组独立同分布的样本，则当随机变量X=x时，非参数核回归函数为：

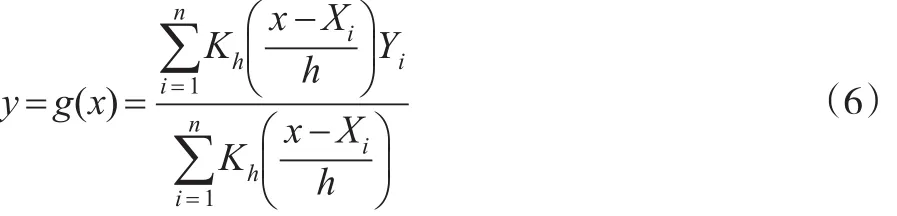
其中，K为核函数，一般核函数为设定的密度函数，h为带宽，本文核函数采用正态核，带宽由交错鉴定法确定。

由分布函数的定义可知，随机变量Y的分布函数的条件回归形式为：

因此利用条件回归的估计形式可得到：

非参数核密度条件分位数为分布函数的反函数，其形式为：

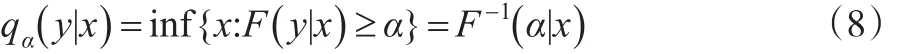
此分位数的估计方法不受数据分布函数的限制，具有良好的适用性与稳健性。

1.3非参数GARCH模型

GARCH类模型是现今主流的计算金融市场波动的工具，目前ARCH与GARCH族模型已得到诸多的扩展。比如GARCH模型不能描述金融市场中的非对称性，即利好与利坏信息对波动影响大小不一致，而EGARCH与TGARCH模型解决了这一问题，ARCH-M与GARCH-M、EGARCH-M模型不仅仅用来描述自回归条件异方差过程，在估计资产的收益时考虑了资产波动因素的影响。但是上述模型都固定了模型的具体形式，在新兴金融市场中充满了不确定性，容易导致模型误设的问题，Bǜhlmann[8]探讨了非参数波动模型模型，通过对比发现某些时候要比参数GARCH模型模型更好的描述金融市场的波动情况，王相宁[9]等研究了非参数可加GARCH模型，可加模型能够克服非参数估计的“维数灾难”问题，使得估计的收敛速度达到与一维的收敛速度一样，本文采用的波动模型的估计方法为非参数可加GARCH模型，下面简述参数GARCH模型与非参数可加GARCH模型。

参数GARCH模型：

均值方程：rt=ut+εtσt

参数GARCH模型通常假设εt服从某种分布，利用极大似然法估计。

非参数可加GARCH模型：

均值方程：rt=ut+εtσt

关于VaR计算的相关内容如上所述，为了验证此方法的有效性，下面利用创业板与中小板股指数据进行估计及检验。

2　实证分析

2.1数据选取及处理

我国中小板与创业板分别在2004年5月与2009年10月启动，中小板主要面向成长期的规模较小的中小企业，创业板主要是为那些处于成长型的、创业期的、科技含量比较高的中小企业提供一个利用资本市场发展壮大的平台，二者都是对主板的有效补充，本文选取了中小板综合指数（399101）与创业板指（399105）进行实证分析，时间范围为2010年8月20日至2016年6月8日共1408组数据，数据从网易下载。收益率采用对数收益率，计算公式为为日收盘价格，数据使用R软件进行处理。

2.2VaR计算结果的检验：KUPIEC检验

对上述两种指数的收益率分别进行ADF检验，由表1的检验结果可知具有平稳性。

表1　ADF检验结果

令rt=u+σtεt，即平均收益为常数收益率，并对两种指数进行ARCH效应检验，通过检验结果说明具有异方差性，而金融数据具有尖峰厚尾性，因此可以应用t-GARCH非参数GARCH模型来描述其收益率的波动。利用t-GARCH模型的估计结果如下：

从估计结果的数值及对应的概率P值可以看出，t-GARCH模型的估计是有效的。本文也利用非参数可加GARCH模型估计波动率，非参数模型只有估计预测的结果，没有模型具体形式，因此不能给出估计表达式。文中用新息项服从t分布与非参数条件分位数两种方法计算出分位数，利用式（3）使用三种方法估计出向前一天VaR的值，分别为非参数GARCH结合非参数条件分位数，参数GARCH结合非参数条件分位数，参数GARCH结合参数t分布分位数，简记：non-non，p-non，p-p，利用似然比检验分别对α=0.05，α=0.025，α=0.01三种情况下来检验三种模型的估计效果，下面具体给出具体的检验结果（见表2），即似然比的P值及对应的失败率（括号内为P值对应下的失败率）。

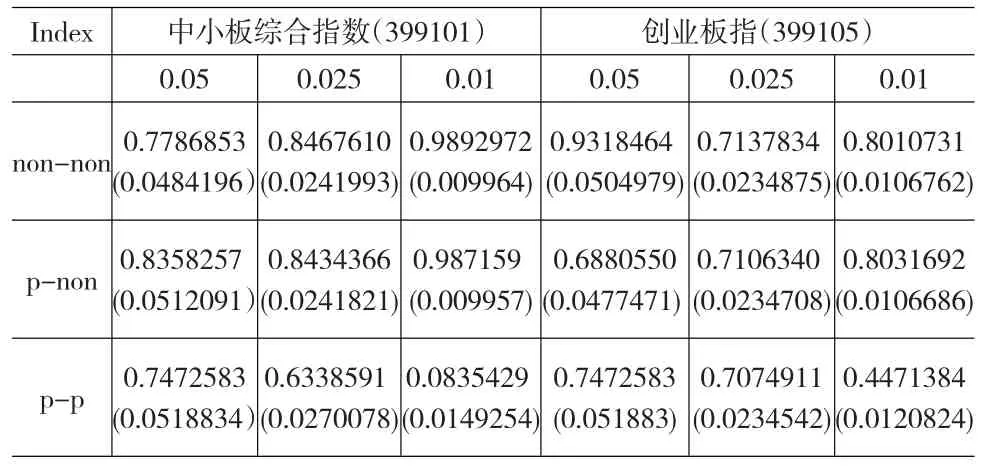
表2　似然比检验结果

从上述检验结果可以看到，三种方法对VaR估计，全部通过了检验，但是运用参数p-p方法时，对应的P值最高为0.7472583，最低为0.0835429，不是很稳定，说明对不同的金融收益序列，不同的置信度，精确度差别较大。并且当α=0.01时，参数方法p-p对应的P值不是很理想，而应用p-non（半参数）与non-non（非参数）的方法，对应的P值几乎都在0.7以上，说明对于不同的收益数据，不同的置信度，p-non（半参数）与non-non（非参数）方法是较稳定的，尤其是非参数方法non-non效果要稍好一些，也就是相对于p-non方法，non-non方法在某种程度上要更加精确一些。目前对于我国的中小板与创业板这样无法达到主板上市要求的市场，尤其创业板市场处于成长阶段，发展不是很成熟，具有较高风险，需要严格监管金融风险，而本文提出的非参数估计方法可以做为在不同置信度下一种可靠的估计方法。

3　结论

由于我国金融市场起步较晚，目前尚在探索发展阶段，随着我国转制过程中金融市场的不断完善，会逐步建立全面的金融风险管理制度与方法，VaR在金融风险管理中也会呈现出重要的地位，因此，需要对VaR进行精确估计。本文提出的非参数方法为得到平稳精确VaR的估计值提供了一种可供参考的方法。VaR能够帮助我们进行风险管理，但是VaR也具有一定的局限性，最明显局限就是不能提供绝对的最大损失额，只能预订在一定置信水平下的损失，在历史形态发生重大变化时，以历史数据为基础的模型就会发生严重问题，一旦发生重大变化，就会发生潜在的错误，现有模型是应对现有风险的，面对转变不再有效，这就产生了转变风险，面对转变风险，无法建立合适的模型来预测，因此利用VaR进行建模时，要对金融市场的突发事件或者异常事件能够充分的估计分析，从此对金融市场进行全面的风险管理。

[1]Engle R F.Autoregressive Conditional Heteroscedasticity With Esti⁃mates of the Variance of United Kingdom Ination[J].Econometri⁃ca.1982,50(4).

[2]Bollerslev,T.Generalized Autoregressive ConditionalHeteroskedastic⁃ity[J].Journalof Econometrics,1986,31(4).

[3]Orhan M,Köksal B.A Comparison of GARCH Models for VaR Esti⁃mation[J].ExpertSystemswith Applications.2012(39),12.

[4]爱民,陈远.我国中小板市场在险价值量的实证研究——基于GARCH-VaR模型[J].南开大学学报(自然科学版).2013.6,46(3).

[5]任继勤单晓彤梁策.中国主板与创业板市场风险比较分析——基于GARCH-VAR方法.《财贸研究》2015,(3).

[6]马薇，卢英，刘月月.大数据条件下金融风险测度的方法[J].统计与决策，2015,(9).

[7]Kupiec P.Techniques Forverifying the Accuracy of Risk Management Models[J].JournalofDerivatives，1995，3(2).

[8]Bǜhlmann P.McNeil A J.An Algorithm for Nonparametric GARCH Modelling[J].ComputationalStatistics&Data Analysis.2002,(40).

[9]王相宁,邹佳，基于广义可加模型的波动率估计方法，中国科学技术大学学报，2008，38（11）.

（责任编辑/刘柳青）

F830.9

A

1002-6487（2016）19-0144-03