基于非平衡面板数据的制造业、服务业与人均收入的统计检验

郭庆然

（河南科技学院经济与管理学院，河南新乡453003）

基于非平衡面板数据的制造业、服务业与人均收入的统计检验

郭庆然

（河南科技学院经济与管理学院，河南新乡453003）

文章选取1980—2011年184个国家制造业、服务业与人均收入水平的非平衡面板数据，利用分位数回归与广义最小二乘法，对三者之间的关系进行实证研究。分位数回归结果发现：随着人均收入水平的逐步提高，人均收入对制造业发展水平产生的创造效应总体上呈现为下降趋势；而对服务业发展产生的创造效应，在服务业发展水平较低时产生的创造效应较大，在服务业发展水平较高时产生的创造效应较小。广义最小二乘法回归结果表明：制造业与人均收入之间存在着显著的负向关系，而服务业与人均收入之间却存在着显著的正向关系。

制造业；服务业；人均收入；分位数回归；广义最小二乘法

0　引言

随着经济的发展和人们生活水平的提高，一个必然出现的现象是劳动力从农业向非农产业转移，随后又会继续出现劳动力从第二产业向第三产业转移，即“配第-克拉克定律”。制造业、服务业作为创造就业的重要产业部门，不仅会影响劳动者收入，而且更会受到劳动者收入水平的制约。近年来，世界各国产业呈现出一种服务化趋势，制造业、服务业的迅速发展和产业结构的演进也由此越来越引起理论界和实践工作者的广泛关注。但现有的大多研究都是从某一国家或地区内部研究制造业、服务业等产业对人均收入的反应，而从跨国家、跨地区视角进行研究、从实证方面进行验证的并不多见。本文则是利用分位数回归与广义最小二乘法，对184个不同发展水平的国家1980—2011年的非平衡面板数据进行实证研究。结果发现：在人均收入提高的过程中，制造业就业比例总体上呈下降趋势，但该下降趋势并不是稳定的。在服务业水平发展的低级阶段，人均收入对服务业产生的创造效应较大；在服务业发展的高级阶段，人均收入对服务业产生的创造效应相对较小。广义最小二乘法回归结果表明：制造业与人均收入之间存在着显著的反向关系，而服务业与人均收入之间却存在着显著的正向关系。

1　指标选取与数据说明

借鉴Fuchs（1980）的做法，选取制造业部门的就业比例为制造业发展的指标，服务业部门的就业比例为服务业发展的指标，人均收入指标选用人均GDP替代。即3个重要指标：制造业就业比例、服务业就业比例和人均GDP，分别表示为：manuratio、servratio和pgdp，并利用消费价格指数对人均GDP进行了修正，转换为1980年不变价格的相应指标。本文数据来源《中国统计年鉴》、《中经网统计数据库》和《国际劳工组织数据库》等1980—2011年184个国家的制造业就业比例、服务业就业比例、人均GDP的数据。但由于部分国家的数据在截面和时间上不能同时获取，故只能采用非平衡面板数据，时间跨度为30年，样本数为2303个。

2　方法选择与样本数据描述

作为截面数据与时间序列数据结合起来的二维数据类型，面板数据有着极其广泛的应用。在利用面板数据对建立的回归模型进行分析时，既要考虑不同时点、不同个体间可能存在着差异，又要考虑不同截面上、不同时点间存在着差异，这在建立模型时就体现为针对不同的时间或截面截距不同。面板数据模型的一般形式为：

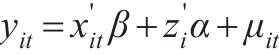
模型中：yit是被解释变量，xit是解释变量，其中i为横截面、t为时间；μit为随机干扰项；为个体或异质性效应，其中zi是包含一个常数项和不随时间变化的一系列变量。

分位数回归（Quantile Regression）是由Koenker和Bassett（1978）提出并引入到经济分析中的，它是对普通最小二乘法（0LS）的一种扩展，提供了解释变量和被解释变量的分位数之间线性关系的估计方法。之后，Bassett (1986)、Powell(1986)和Chernozhukov(2002)等在上述基础上进行了深化研究。与普通最小二乘方法相比，分位数回归存在如下优势：（1）分位数模型比较适合估计具有异方差的模型；（2）分位数回归不需要对模型中的随机误差项作任何分布的假定，当误差项为非正态分布时，其参数估计效果比最小二乘法更为有效；（3）分位数回归参数估计量较最小二乘方法参数估计量更为稳健；（4）分位数回归反映的是解释变量对被解释变量在特定分位数上影响的边际效果，而最小二乘法回归反映的只是解释变量对被解释变量影响的平均边际效果。显然，分位数回归具有最小二乘法回归无法比拟的优势。分位数回归方法的基本模型为：

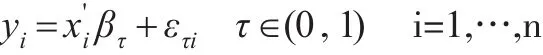
模型中的yi是被解释变量，xi是解释变量，βτ为对应于被解释变量第τ分位数的解释变量的回归系数，ετi是随机干扰项。在给定解释变量xi时，y的第τ个条件分位数为分位数回归的参数估计采用加权绝对离差最小（WLA）准则进行判断。可以通过求解下式的极值得到分位数回归系数的估计量：

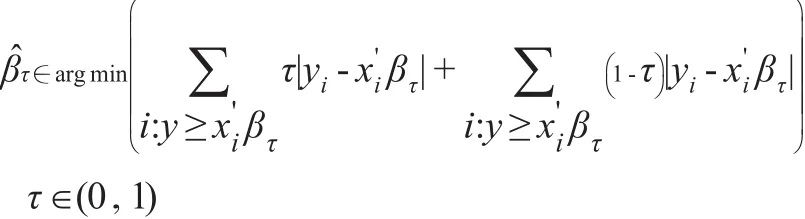
将分位数回归与面板数据模型结合起来对变量之间的关系进行分析，能够较好地在控制个体异质性的基础上研究被解释变量条件分布的不同分位点上变量之间的关系。为了克服原有分位数回归方法中没有考虑固定效应这一缺陷，Koenker提出了面板分位数回归方法，并构建模型如下：

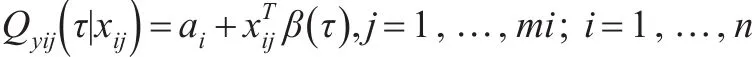
其中，i和j分别代表个体与时期。可以利用下式的优化对这一问题进行求解：

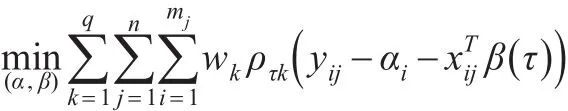
其中，τk代表分位点；wk代表权重；ρτ(μ)=μ(τ-I(μ＜0))。在Koenker模型的基础上，CAR0SLAMARCHE(2006)对PQR估计方法进一步进行探讨，并结合实际数据进了实证分析。本文将分别利用面板数据分位数回归、面板数据广义最小二乘法研究制造业发展水平、服务业发展水平对人均GDP异质性的反应程度及其相关性。制造业就业比例、服务业就业比例与人均GDP的统计性描述见表1。相关变量的统计性描述结果初步表明，184个国家的人均GDP均存在明显差异，最大值和最小值之间相差较大。可以认为，解释变量人均GDP相差悬殊决定了各个国家的制造业就业比例、服务业就业比例存在较大差距。

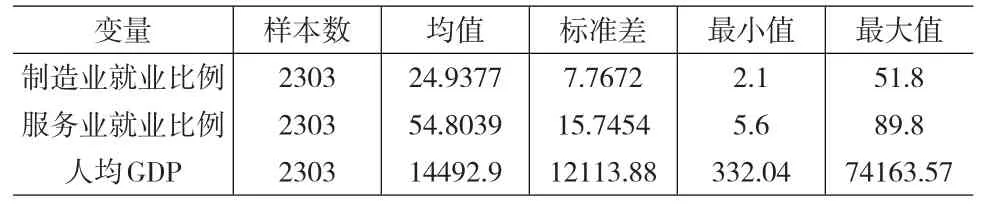
表1　样本数据的统计描述

3　模型检验与模型设定

由于对数据取自然对数并不改变变量之间的面板协整关系，而且可以消除可能存在的异方差，所以对manuratio、 servratio和pgdp进行自然对数变换。本文分析工具采用计量经济分析软件Eviews7.2和stata12.0。（1）变量平稳性检验。对变量manuratio、servratio、pgdp以及lnmanuratio、lnservratio、lnpgdp分别进行平稳性检验，结果发现所有变量均为一阶单整，即I（1）；（2）面板协整检验。利用E-G两步法对lnmanuratio、lnpgdp进行协整检验，结果发现lnmanuratio和lnpgdp之间存在协整关系。同理，可检验出lnservratio和lnpgdp之间也存在协整关系。根据所要研究的问题，本文设定如下计量模型：

模型（3）：ln manuratioit=αi+β1ln pgdpit+εit

模型（4）：ln servratioit=αi+β2ln pgdpit+εit

其中，模型（1）、模型（2）为面板数据分位数回归模型；模型（3）、模型（4）均为面板数据固定效应模型。模型中i代表国家，为184个国家，t表示样本观测时期，为1980—2011年，τj为分位数，为0～1之间的分位数。ln manuratioit为制造业就业比例的自然对数，ln servratioit为服务业就业比例的自然对数，ln pgdpit代表人均GDP的自然对数。

4　实证分析

与最小二乘方法相比，分位数回归方法放宽了对随机干扰项分布假设的限制，约束条件大大减少，对异常值更具包容性，估计结果更具稳健性。对面板分位数回归模型（1）、模型（2）分别进行估计，分位数取0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，回归结果见表2所示。

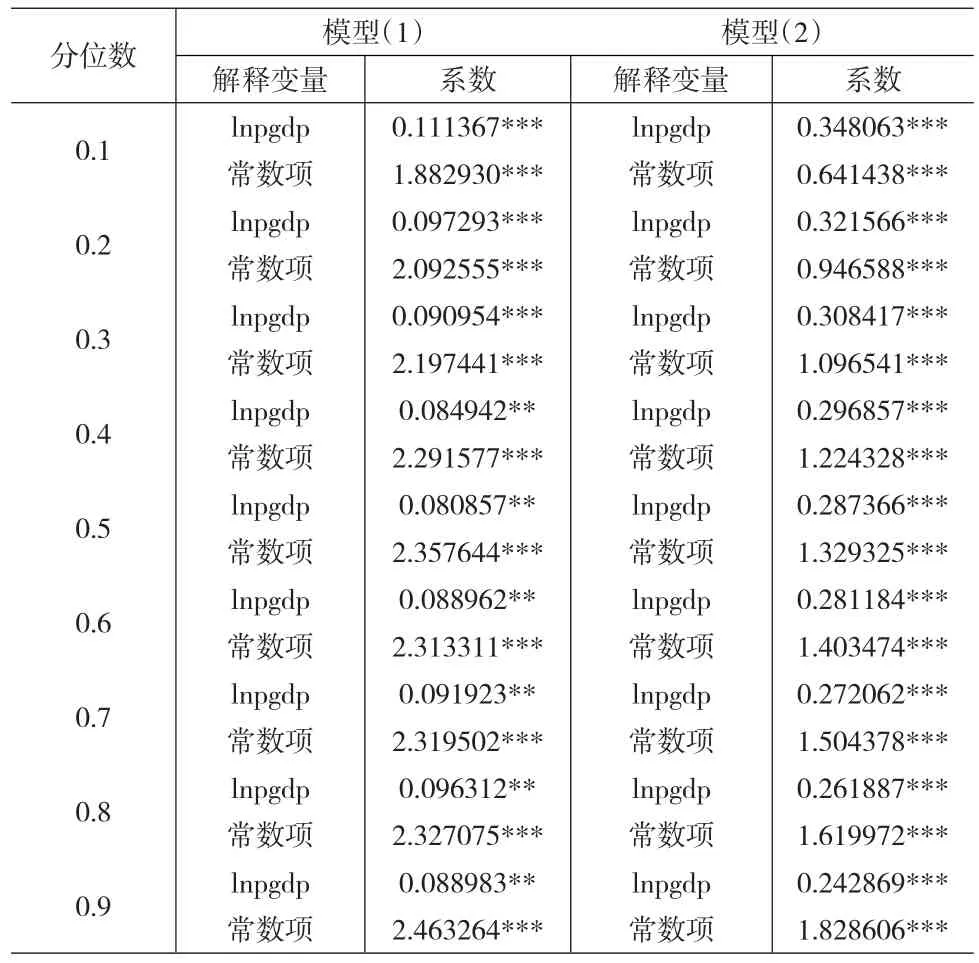
表2　制造业就业比例与人均收入的回归结果

表2中的结果显示：对于模型（1），lnpgdp的回归系数全部为正值，并且随着分位数的持续增加，lnpgdp的系数变化规律为先减小后增加再减小（见图1）。分位数回归系数表示解释变量对被解释变量的某一特定分位数的边际效果，即在制造业就业比重的某个分位段上，制造业就业比重对人均GDP的反应。表2中的回归结果显示，制造业发展水平较低的国家与制造业发展水平较高的国家人均GDP的创造效应有明显差异。0.1分位数对应的是制造业就业比重相对较低的国家，当它们的人均收入增加1%时，制造业就业比例将增长0.11个百分点；而0.9分位数则对应一些制造业就业比重相对较高的国家，当其人均收入增加1%时，制造业就业比例将增长0.09个百分点。即制造业的就业比重对人均GDP的反应随着分位数的提高呈现出先减小后增加再减小的曲线变化，但总体上看呈递减趋势。这意味着人均收入变动对制造业产生的创造效应，随着制造业的变动先减小、后增加、再减小。即总体趋势是减小的。这恰好显示了贫穷国家、发展中国家和发达国家的制造业发展水平随人均收入水平的变化轨迹。对于贫穷国家，最可能的解释是自己制造不如进口；对于大部分发展中国家，随着人均收入水平的提高，制造业发展水平也越来越高；而对于发达国家，随着人均收入水平的提高，制造业发展水平会逐步下降。该结果对英国、美国等发达国家以制造业为主的第二产业所占比例越来越小而发展中国家第二产业所占比例越来越大的现象给予了有力的解释。

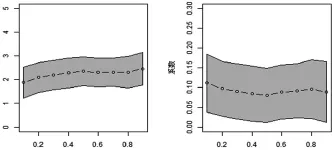
图1　ln manuratioit不同分位点下的变量系数

模型（2）中，lnpgdp的回归系数全部为正值，且随着分位数从0.1到0.9，lnpgdp的回归系数从0.35减小到0.24（见图2）。显然，与模型（1）相比，lnpgdp的系数随分位数的增加而持续下降。即在分位数回归框架之下，服务业就业比重对人均GDP的反应随着分位数的提高逐渐减小，人均收入增加对服务业产生的创造效应随着服务业发展水平的提高而逐渐降低。该结果与Fuchs（1980）、解栋栋（2009）的结论相一致。

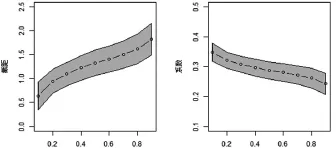
图2　ln servratioit不同分位点下的变量系数

对于面板数据模型来说，普通最小二乘法（0LS）估计会导致偏误。因此，在选择估计方法之前，必须通过检验进行固定效应模型、随机效应模型的筛选。这里运用Hausman检验进行模型的选择，Hausman检验的结果发现，选择面板数据固定效应模型进行估计更为合适。考虑到时间跨度较长、个体较多，故需要考虑相关性、异方差等问题，经过检验发现模型（3）、模型（4）的误差项无论在时间维度，还是截面维度上均存在相关性，因而采用广义最小二乘法进行估计，并对误差进行了修正。回归结果见表3所示。

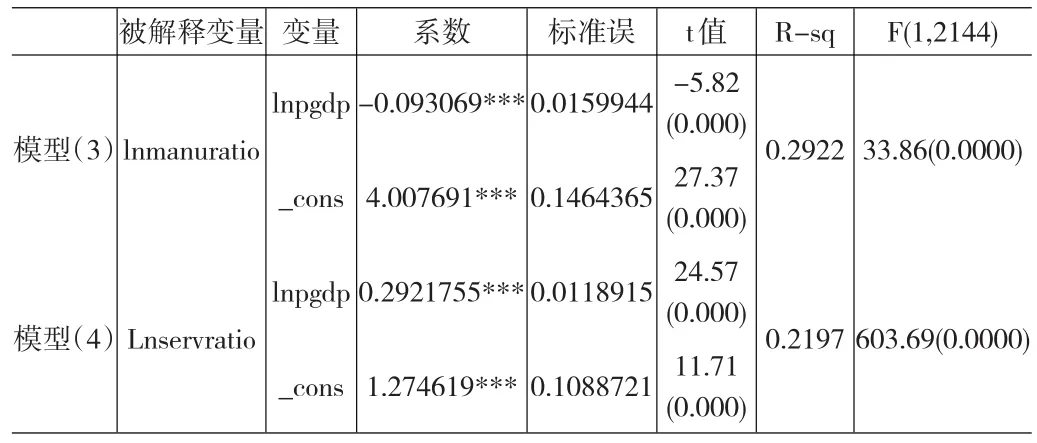
表3　制造业、服务业就业比例与人均GDP个体固定效应回归结果

模型（3）、模型（4）为面板固定效应模型采用广义最小二乘法估计的结果。利用最小二乘法估计出的系数与分位数回归估计的结果是截然不同的。由于个体较多，故模型（3）、模型（4）的截距不是被关注的对象。模型（3）中，lnpgdp的系数为-0.09，即人均GDP每增加1%时，制造业就业比重将平均减少0.09个百分点。这与表2的分位数回归结果中，人均收入增加对制造业发展产生的创造效应总体趋势是减小的结果基本一致；模型（4）中，lnpgdp的系数为0.29，即人均GDP每增加1%时，服务业就业比重将平均增加0.29个百分点。即制造业就业比重、服务业就业比重的人均GDP弹性分别为-0.09和0.29。显然，都是缺乏弹性的。

图3　分位数回归拟合曲线

图3中虚线为ln manuratioit对lnpgdp的0LS拟合线，其它为分位数回归的拟合线。各拟合线从下到上对应的分位数分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9。图3表明了在一定的人均收入水平上制造业就业比重随人均收入的变化。不同分位数回归直线之间的间隙中间窄、两边宽，中位数回归直线（τ=0.5）与0LS拟合直线相交：（1）在交点右侧，中位数回归直线处于0LS拟合直线的下方，这说明该部分制造业就业比重是左偏的；（2）在交点左侧，中位数回归直线处于0LS拟合直线的上方，说明该部分制造业就业比重是右偏的。图3还显示，中位数回归直线与0LS拟合直线的位置明显不同，说明了条件密度并不对称。

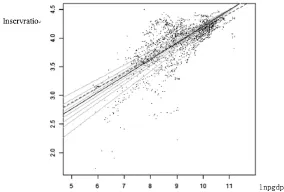
图4　分位数回归拟合曲线

图4中虚线为0LS拟合直线，其他为分位数回归拟合直线。各拟合线从下至上对应的分位数分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9。图4表明了制造业就业比重随人均收入增长而变动的趋势。不同分位数回归直线之间的间隙中间窄、两边宽，中位数回归直线（τ=0.5）总体上位于最小二乘拟合直线之下，说明服务业就业比重是左偏的。处于两侧的分位数回归直线之间的间隙较宽，说明了该部分数据点比较分散；处于中间的分位数回归直线之间的间隙较窄，说明了该部分数据点比较密集。图4还显示，中位数回归直线与0LS拟合直线的位置基本相同，说明条件密度基本对称。

5　结论

利用1980—2011年184个国家制造业、服务业与人均收入水平的非平衡面板数据，利用分位数回归与广义最小二乘法，对三者之间的关系进行实证研究。基本结论可以归纳为：

（1）制造业部门就业比例与人均收入之间大体上呈现负相关关系

制造业部门就业比例与人均收入之间并非总是存在着稳定的负相关关系，但大体上呈现负相关关系。该结论不但与“配第-克拉克”定律不矛盾，也恰好从实证方面证明该定律的正确性，广义最小二乘法回归结果也同样证实了这一点。随着人均收入水平对制造业就业水平的影响可以分为三个阶段：在人均收入水平较低时，制造业部门就业比例逐渐下降，这最有可能是因为这些地区的劳动者技能水平不高、技术水平落后等引起的，或者是由于收入水平太低引起消费需求不足引起的，处于工业化前期、初期的国家大多位于这一阶段；随着人均收入水平的提高，制造业就业比例会有所提高，处于工业化中期、后期的发展中国家大多处于这一阶段。这一结论也解释了包括中国、印度、巴西等发展中国家的制造业发展轨迹；当人们的收入水平提高到一定程度之后，制造业部门的就业比例会趋于下降，处于后工业化社会的发达国家都处于这一阶段。英国、美国、日本等世界制造中心的转移与变迁路径也说明这一点。

（2）服务业部门就业比例与人均收入之间存在着稳定的正相关关系

服务业部门就业比例与人均收入之间存在着稳定的正相关关系，这一结论与Fuchs(1980)、解栋栋（2009）的实证研究结论基本吻合。分位数回归结果显示：人均收入随着服务业发展水平的不同对服务业就业的创造效应呈现出动态变化，表现为不同分位数下的斜率系数存在着显著差异。在服务业发展水平较低时，收入水平带来的需求效应对服务业发展的创造效应较大；在服务业发展水平较高时，收入水平带来的需求效应对服务发展的创造效应较小；服务业发展水平与人均收入在保持稳定正相关的同时，还具有逐渐收敛的倾向。

上述结论虽然是根据184个国家1980—2011年的非平衡面板数据得到的，但对我国制造业、服务业发展的经济政策仍具有一定的借鉴意义。

[1]Koenker GY BRW,Koenker A RW.Strong Consistency of Regres⁃sion Quantilesand Related Empirical Processes[J].Econometric Theo⁃ry,1986（2）.

[2]阿瑟·刘易斯.二元经济论(施炜、谢兵、苏玉宏译)[M].北京：北京经济学院出版社，1989.

[3]姚先国，来君.二元社会结构中的工资决定模型与人口流动[J].财经研究，2005,（8）.

[4]徐佳宾.产业升级中的中国劳动成本优势[J].经济理论与经济管理，2005,（2）.

[5]胡放之.提高初次分配中劳动报酬比例促进经济健康发展[J].贵州社会科学，2009,（6）.

[6]殷庆坎.工资水平对产业结构高级化作用机制的理论评述[J].资料通讯，2007,（8）.

[7]解栋栋.服务业发展与人均收入的关系：基于分位数回归的实证研究[J].当代财经，2009,（8）.

（责任编辑/浩天）

F719

A

1002-6487（2016）19-0122-04

2015年度河南省高校科技创新人才支持计划项目（人文社科类）；河南省高等教育教学改革研究项目（2014SJGLX274）

郭庆然（1972—），男，河南西华人，博士后，教授，研究方向：数量经济与产业发展。