基于层次贝叶斯方法的关键词广告转化率影响因素研究

覃朝勇

（广西大学数学与信息科学学院，南宁530004）

基于层次贝叶斯方法的广告转化率影响因素研究

覃朝勇

（广西大学数学与信息科学学院，南宁530004）

搜索引擎

广告中，如何对

广告效果进行评估是当前的一个研究热点和难点。文章构建了基于层次贝叶斯方法的转化率实证模型，利用马尔科夫蒙特卡洛方法进行参数估计，并将模型应用于某公司3个月的百度竞价数据。结果表明，热门地区的转化率较偏远地区更高；排名位置靠前的广告转化率也更高，排名位置对广告转化率的影响还和企业的知名度（或市场地位）有关；

特性中，

长度、

是否包含商标信息和城市信息都显著影响

广告的转化率。

广告；层次贝叶斯；点击率；转化率；MCMC

0　引言

当前，竞价排名广告服务已经成为了搜索引擎商最大和增长最快的收益来源[1]。搜索引擎商提供的[2,3]。不同于传统的广告，广告商仅在

广告中广告被点击时付费，广告商在广告活动中的主要任务是管理

和每个

的出价，以最大化自己的广告效果。在实际的广告活动中，广告商通常管理着成百上千的

。如在中文百度

广告中，每个广告商管理多个推广计划，每个推广计划由多个推广单元组成，而每个推广单元中都包含着多个不同的

。然而，在众多的

中，有些

被用户搜索的次数明显要超过其余

，有些

的点击率、转化率很低，许多

的转化率甚至为零。如何选择

以及如何对

进行竞价并对

广告效果进行评估，是广告商重点关心的问题，也是当前的一个研究热点和难点。

广告具有很强的针对性，通过搜索

能为企业准确锁定目标客户，

广告已经成为了企业扩大产品销量和提升品牌的重要营销手段

基于以上背景和问题，本文对影响广告效果的相关因素进行了研究，构建了层次贝叶斯转化率实证模型，利用马尔科夫蒙特卡洛(MCMC)方法对参数进行估计，并应用于某科技公司在百度上3月的竞价数据。

1　基于层次贝叶斯的转化率影响因素模型

1.1影响转化率因素分析

影响广告转化率的因素众多，如涉及消费者的因素、涉及广告商及产品的因素、搜索引擎商的因素以及环境因素等等，要将所有的这些因素考虑进来是将是非常复杂的，也是没有必要的。本文从消费者行为角度出发，将考虑的范围限定在与

和链接项所呈现的特性上。百度

广告竞价中，转化是指潜在客户完成一次广告商期望的行动，与广告商的推广目的和对推广效果的定义相关，而不仅仅局限于购买行为。转化可能指潜在客户：在网站上停留了一定的时间；浏览了网站上的特定页面，如注册页面，“联系我们”等页面；在网站上注册或提交订单；通过百度商机中心、网站留言或网站在线即时通讯工具进行咨询；通过电话进行咨询；上门访问、咨询、洽谈；实际付款、成交（特别是对于电子商务类网站）。

排名位置：已有的许多研究表明，用户的点击行为和广告的排名位置有关，但广告排名位置和转化率的关系究竟如何，是否排名位置越靠前，转化率就越高？这些都值得深入研究。

推广区域：在百度推广中，推广区域分热门地区和偏远地区。显然，不同地区的消费者在经济水平、消费习惯和环境等方面存在差异，这些差异是否影响以及如何影响转化率？

特性：用户的搜索习惯还反映在

本身的特性上，

的特性包括了

长度、

是否带有品牌和商标和是否带有城市信息等。这些特性是否对转化率有影响以及如何影响转化率，都是广告商迫切需要了解的。

Ghose等[4]还考虑了页面质量的对转化率的影响，但他们收集的是不同广告商的竞价数据，而本文收集的是同一个广告商的竞价数据，页面质量是固定的。文献Rutz[5]在研究转化率时，还考虑了点击率(CTR)和每点击成本(CPC)的影响。CPC为广告被点击1次广告商所付出的成本。然而我们分析认为，排名位置和CTR及CPC之间存在一定的相关性，排名位置好，位置吸引力强，则CTR应该会高，对应的CPC也会高，因此，排名位置和CTR及CPC间有相关性。对本文搜集的数据进行相关性分析的结果也表明，CTR和排名位置、CPC和排名位置在.01水平（双侧）上都显著相关。

1.2模型建立

以下我们以最大化广告商转化率为优化目标，从排名及特性角度去研究影响转化结果的因素，如前所述，本文暂未考虑诸如广告网页质量和产品特性等广告商本身其它因素对转化结果的影响。

假设某个广告商选定n个wi(i=1，…，n)进行广告竞价，cij是wi在周期j内的点击量，点击率为pij，转化次数为qij。在返回搜索结果页面后，消费者决定是否完成广告商期望的行动可以用消费者离散选择模型来刻画:

其中，Pconv为转化概率，u为消费者效用函数，该效用函数由排名位置、以及特性等决定。i在周期j内被观察到的转化次数服从二项分布：

w

其中，c为被点击次数，q为转化次数。在观测的周期T内，我们有似然函数：

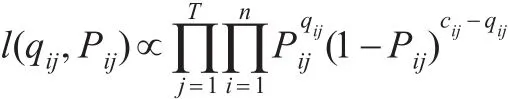
根据以上分析，不同的存在异质性，为了反映这种异质性和随机性，我们使用层次贝叶斯模型来进行拟合。结合所选数据的行业特征，对每个

w，我们构造了如下的效用函数：

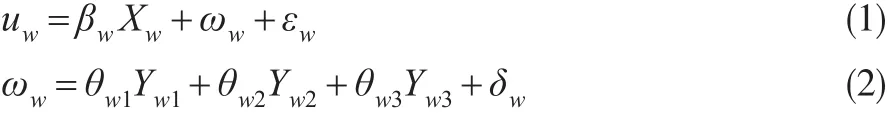
式（1）中，βw为待估参数（包含了截距）且β～N(μβ，vβ)，Xw为变量，包括排名位置以及推广地区，εw为误差项。ωw为关键词本身特性的影响，θw为待估参数（不含截距）且θ～N(μθ，vθ)，关键词特性Yw1～Yw3分别表示关键词长度、是否带有品牌和商标信息（0表示不带，1表示带有）以及是否带有具体城市信息（0表示不带，1表示带有）。δw为关键词误差项。模型中各参数的先验概率分布如下：β～N2(μβ，vβ)，其中μβ～N(μb，Vb)且协方差阵由于先验信息很少，故取θ～N3(μθ，vθ)，其中=1000I3。关键词误差项δw～Gamma(k/2，m/2)

1.3基于马尔科夫链蒙特卡洛模拟的模型参数估计

在建立的模型中，β和θ是待估参数。由贝叶斯理论可知，给定样本数据D后的后验参数分布函数f(β，θ|D)如下：

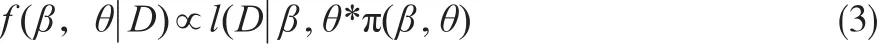
式中，1(D|β，θ)为样本联合概率分布即似然函数，π(β，θ)为参数β和θ的先验概率分布。β和θ的后验分布设计高维积分运算，其解析表达式无法直接给出，因此考虑采用马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)方法来进行参加估计。MCMC抽样方法有多种，而在贝叶斯分析中应用最为广泛的MCMC方法主要有两种：Gibbs抽样(sampler)方法和Metropolis-Hastings（M-H）方法。当全部参数的条件概率分布都可以以解析表达式给出的时候，可以使用Gibbs抽样方法依次迭代取样。当无法推导出各参数的满条件分布时，可以使用比Gibbs抽样更一般的MCMC方法：M-H方法。在本文中，我们将两种方法结合使用，具体算法描述如下：

MCMC模拟抽样迭代算法：

第一步:对每组，计算自然函数；利用极大化自然函数估计效用值。

第二步:对每组，使用M-H算法抽样出新的参数，计算接受概率并判断是接受还是拒绝新参数，初始值β0和θ0取极大似然估计值；

第三步:对每组，计算，其中ωw～N(θwYw，δm)

第四步:使用Gibbs方法对参数μβ和vβ进行抽样：从π(μβ|β，vβ)中产生新的μβ，其中，；从π(vβ-1|β，μβ)中产生新的vβ，其中，

重复步骤1～4。

调整参数，使得接受概率大概为20%左右，然后运行10000次，剔除迭代前2000次，从2000次以后隔100次取样一次，作为估计参数的样本。另外，由于数据原因，在迭代过程中，很容易出现病态矩阵，且矩阵数很大，对系数矩阵很小的扰动都会导致求得的逆矩阵差别很大，不利于参数的估计，本文使用广义逆矩阵来解决该问题。

2　实证分析

2.1数据来源及分析

本文的数据来源于一家在国内最早从事网络服务的公司，该公司自2010年起开始在百度搜索进行产品推广。考虑到节假日因素，我们避开了国家法定节假日较多的月份，收集了公司2011年6～8月份的竞价数据，数据以一个星期为一个统计时间单位。数据包含了每个关键词的竞价时间、推广地区、印象数、点击数、平均排名、每点击成本CPC（点击数/总花费）和转化数。本文只选择了点击数大于0的数据，因为若点击量为0，则转化数以及花费也均为0，对于搜索引擎商和广告商来说，都没有带来直接的利润。结果包含了564个关键词共10301条数据记录中的468个关键词，共5269条记录数据，数据描述性统计如表1。

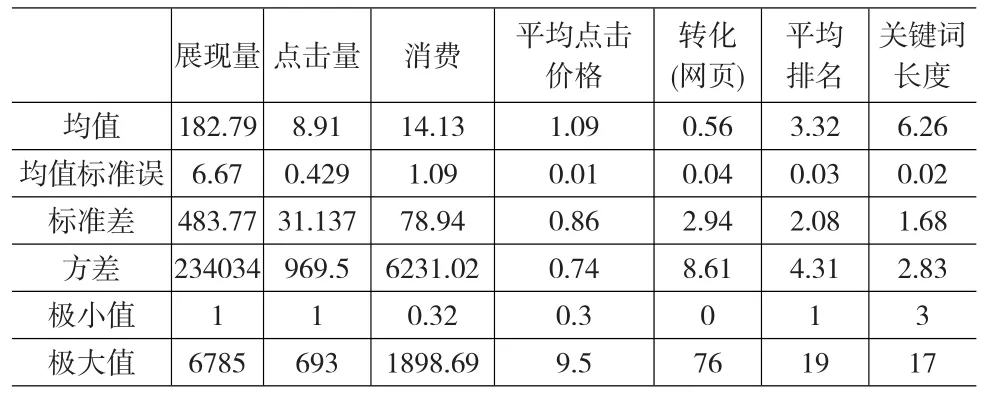
表1　数据统计量

由表1可知，该企业广告的平均展现量(impression)为182.79，平均排名为3.32，的平均长度为6.26，但平均转化只有0.56。在收集的时间周期内，该公司平均323个展现量能得到1次转化，或者是平均每15次对该公司广告的点击能得到1次转化，每次转化的平均价格为25元，每次点击的平均花费1.09元。在本文考虑的周期内，公司在该组产品上的

广告共花费了￥7448。由表中数据可知，所收集的数据在展现量、点击量以及消费上的方差非常大，说明不同的

的广告效果存在较大的差别。在

特性上，我们考虑了

的长度、

是否带有商标和品牌名称以及

是否带有城市信息。在468个

中，30个

带有商标和品牌信息（如“aofax传真服务器”），55个

带有城市信息。

2.2结果分析

利用MCMC模拟方法对本文的层次贝叶斯模型中的参数进行估计，结果如表2所示。由表2可知，截距均值为-12.215且结果是显著的。在所有估计的参数中，截距值是最小的，可知总体的转化率是比较低的，因为截距值越小，效用值也就越小，对应的转化率也就越低，这个结论和前面的统计结果是相符的。

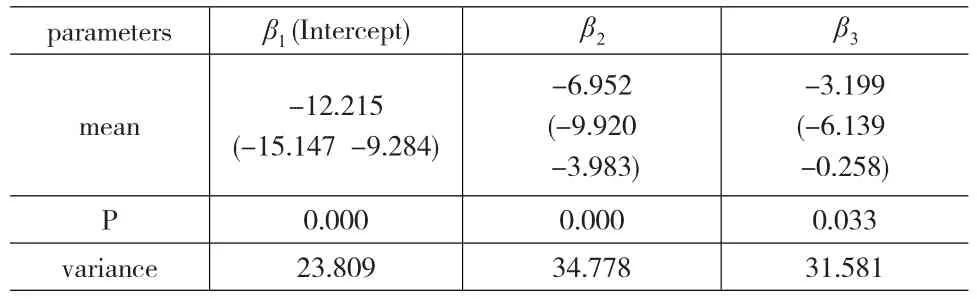
表2　参数估计结果(β)

目前已有的研究中，未见有对推广地区因素的考虑。本模型中，推广地区的影响参数估计检验结果是显著的，均值为-6.952。由于在数据处理时，由热门地区到偏远地区是按升序进行排列，故数值越大说明地区越偏远。因此可以得出结论，热门地区的转化率要高于偏远地区的转化率。同时，由源数据可以看出，热门地区的点击量和转化数都要明显高于偏远地区，本文收集的竞价数据是针对网络办公软件的，可以认为热门地区的办公信息化程度要高于偏远地区，这符合人们的常识。

位置排名对转化率的影响：直观上，排名越靠前，点击率和转化率也越高，Ghose等[4]和Rutz[5]的研究均证实了这一观点，表2中的参数估计结果也支持了这一结论，即排名位置和转化率是负相关的，因为排名位置越靠前则数值也就越低（如排名最前的为1），转化率也就越高。另外由表1可知，该企业的广告平均排名位置较高，达到3.32。位置排名是关键词广告中最重要的一个因素，广告成本、点击率、转化率以致最终的利润都和广告排名位置有关系，国外研究者们在这方面取得了相当多的研究成果。如Ghose等[4]认为竞价排名中位置靠前的广告虽然能带来高的点击率和转化率，但是带来的利润却不如排在中间的广告。Kinshuk等[5]认为一个优良的企业就算竞价排位低于非优良企业（inferior）的广告位置，仍然获得多于非优良企业的点击。本文认为，这种悖论源自于行业品牌认知度。在品牌认知度非常高的行业，知名企业（对应于Kinshuk的superior firms）的广告即使不排在最前，也能获得较高的点击率和转化率。但是要完全探讨排名和转化率的关系则是个非常复杂的问题。广告位置靠前，可能会带来两个不同的影响。首先，从消费者观点出发，位置越靠前，则对该广告产品质量的信任度也就越高。这种影响类似于消费者更信任在中央电视台黄金时段播出的广告，而对其它时间段播出的广告信任度则会下降。因此，这种观点认为位置好的广告就能带来高的转化率。但Agarwal等[7]认为，没有真实购买意向的顾客倾向于点击排名靠前的广告但是并不购买，而那些有真实购买意向买主由于近期偏好则会点击排名中间的广告并购买产品。本文研究对象企业所属的行业，品牌认知度并不是非常高，不存在少数寡头企业垄断市场的现象（如智能手机行业），所以第一种影响大于第二种影响，即排名位置越靠前，转化率也就越高。

除了以上讨论的影响因素外，本身的特性也会影响到转化率，若忽略这些参数的影响，将会造成对别的参数估计的偏差，参数估计结果如表3。

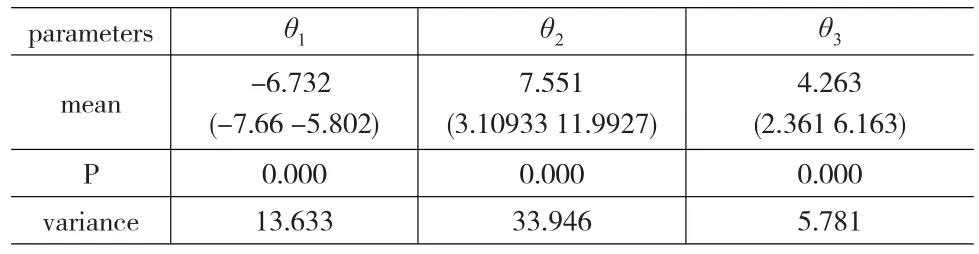
表3　参数估计结果(θ)

源数据中核心词长度为4，最低值为3，最高值为17，均值为6.26。1值为-6.732，且结论显著。该参数结果说明[5]认为，长的

能带来更高的点击率，但并未带来高的转化率。这些研究结论上的差异可能源自于数据本身的差异性，因为前者搜集的是多个行业的竞价数据，而后者仅为酒店行业的数据。

的长度显著影响转化率，

长度越长，转化率就越低。这说明如果用户输入较长的

，则很可能是用户想了解同类产品的价格、功能以及如何使用该类产品，用户的这些行为最终并未带来转化。而在Ghose的研究中，

长度对于转化率的影响并无显著统计意义。Rutz

长度影响参数θ

广告推广的是否带有商标（参数θ2）显著影响着转化率，参数值高达7.551，且结论具有显著的统计意义。说明该公司的产品在行业中具有很强的影响力，这和现实相符合，因为该公司是最早成功研发出该产品的公司之一。该结论与Rutz[5]的研究结论一致，但与Ghose等[4]所得结论相反，究其原因，我们认为该不同源于收集数据的行业存在差异，因为我们收集的是特定公司产品的竞价数据（Rutz也如此），而并未跨行业和跨公司，但Ghose的研究并不是针对某类特定行业和产品的。同样，3）显著影响转化率，参数值达到4.263，说明有真实购买意向的用户在搜索时倾向于使用带有城市信息的

。

是否带有城市信息（参数θ

2.3研究结果对于广告商管理广告的意义

正如前面提到，考虑本身特性对转化率的影响是必要的，若忽略这些参数的影响，将会造成对别的参数估计的偏差。为了更好的说明这个问题，假设我们在模型中不考虑3由负值变为正直，排名位置和转化率正相关，显然和实际情况相悖。这表明了当不考虑

特性时，本应是

特性对转化率带来的影响效果被强加到各参数上，使得参数估计值被放大。由此可见，

特性因素在评价

转化率效果中具有重要的作用，可以帮助广告商更好的从

层面上去优化广告活动。

特性，而其它参数及设置均不变，参数的估计结果如表4所示。对比表2可知，不考虑

特性时，各个参数值均变大，其中β

*95 percentconfidence interval

parameters mean P variance β2β30.600 (-2.860 4.061) 0.417 0.173 β1(Intercept) -8.905 (-12.067-5.743) 0.000 6.449 -3.812 (-6.692-0.932) 0.009 4.461

本文研究结论的重要意义在于：可以从层面对转化率进行评估，而这对广告商是非常有益的。为了评价

并预测转化率，广告商通常的做法是选择部分

（包括引擎商推荐的

）进行竞价广告，通过一段时间后对

广告效果进行评估，然后再调整

集合中

的组成并进行竞价广告，然后再评估调整，该过程需要不断重复。显然，这种做法通常会花费更多的资金和人力，且效果也受到质疑。利用本文的研究结论，可以缩短寻找最佳

集合的时间并减少花费。

具体来说，本文的研究对广告商具有如下指导意义：

(1)在考虑转化率为目标时，应考虑在热门地区竞价排在第一页的，且

长度不宜太长（6个字以内），

最好是带有城市信息和商标信息。

(2)在进行竞价时，应根据所属的行业特性来考虑目标理想排位。在人们对品牌认知度非常高的行业，如果属于知名度非常高的企业，则无需对排名最靠前的几个位置进行竞价也可获得相同的广告效果；如果企业属于非知名企业，排名越靠前广告效果越好。而在品牌效应一般或者是人们对该行业品牌认知度不是很高的行业，企业应竞价获取排名靠前的广告位置。显然，本文所研究的行业属于后者。

(3)引擎商在给广告商提供广告时，会向广告商推荐

，但并不公布推荐的具体依据。结合本文研究结论，以

可观测到的特征对

转化率进行预测和评估，广告商就能更好的理解

广告并能更准确的选择

进行竞价。

3　结束语

本文从角度对影响广告转化率的相关因素进行了分析，包括推广地区、排名位置以及

特性，构建了层次贝叶斯转化率影响因素分析模型，利用马尔科夫蒙特卡洛(MCMC)方法对参数进行估计。对某企业网上办公软件广告3个月的竞价数据进行了分析，研究结论为广告商更好的管理

广告提供了借鉴。

本文研究的数据和结论是针对互联网中的一个特定行业，结果也仅局限于类似行业中，如何拓展到更多不同的行业是作者下一步的研究方向。此外，本文在选择关键词时，以周为统计单位，将在一周内转化率为0的关键词都排除在外，但该关键词按月统计的转化率可能大于0，如何考虑及评价这类关键词的广告效果值得进一步研究。

[1]阳成虎,杜青龙.基于保留价格的竞价模型研究[J].西南交通大学学报(社会科学版).2009,10(4).

[2]Jansen B J,Mullen T.Sponsored Search:An Overview of the Concept, History,and Technology[J].International Journal of Electronic Busi⁃ness，2008,6(2).

[3]Ghose A,Yang S.An Empirical Analysis of Search Engine Advertis⁃ing:Sponsored Search in Electronic Markets[J].Management Science. 2009,55(10).

[4]Rutz O J,Bucklin R E,Sonnier G P.A Latent Instrumental Variables Approach to Modeling Keyword Conversion in Paid Search Advertis⁃ing[J].JournalofMarketing Research.2011,49(3).

[5]Jerath K,Ma L,Park Y,et al.A“Position Paradox”in Sponsored Search Auctions[J].Marketing Science，2011,30(4).

[6]Agarwal A,Hosanagar K,Smith M.Location,Location and Location: An Analysis of Profitability of Position in Online Advertising Markets [J].Marketing Research，2011,48(6).

（责任编辑/易永生）

F224

A

1002-6487（2016）19-0064-04

国家自然科学基金资助项目（71462002）；广西自然科学基金资助项目（2013GXNSFAA019340）

覃朝勇（1975—），男，广西河池人，博士，副教授，研究方向：决策分析和运营管理。