联接性学习：促成数学学习的有效建构

2016-12-08顾小龙

考试周刊 2016年92期

顾小龙

数学学习总是以一定经验和知识为前提，在联想的基础上更好地理解和掌握新知，这里的联想指知识的联结过程，教学中总是会出现学生对新知识理解不够，不能运用知识解决实际问题的现象，很重要的一个因素是老师没有组织学生进行有意义的学习，没有找到新旧知识之间的内在联结，没有帮助学生建立有效的、稳固的认知结构，这里讲到的认知结构，就是学生通过自己积极主动的认识在头脑里建立起来的数学知识结构。数学学习过程本身就是一种认识活动，数学教学的根本任务是发展学生数学认知结构，而数学认知结构是由数学知识结构转化而来的，要建立学生数学认知结构，必须以学生数学知识结构为基础，进行开发和利用，从而生成新的数学认知结构，实现对知识的内化，达到对知识本身的深刻理解甚至超越。本文以《解决问题的策略：画图》一课对数学联结性学习做一些初步探索。

一、找准学生的认知起点，引发学生的内在需求

环节1：引入部分。

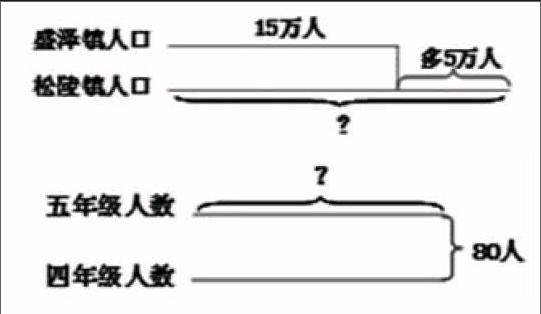
1.师：解决问题的策略大家学习过吗？现在有两个问题请大家看一下。出示图1，学生观察，问：从第一张图中你看到什么条件和问题呢？

学生答：松陵镇人口比盛泽镇多5万人；盛泽镇有5万人；松陵镇有多少人？师：刚才大家从图中找了条件及数量之间的关系，很快解决了。

2.出示图2，问：从中你看到了什么条件和问题呢？

学生答，并列式：（80÷2=40人）

师：为什么可以用80÷2呢？学生答：因为两个年级的人数一样。师：也就是说80人和五年级人数之间有怎样的关系呢？（80人是五年级人数的两倍）

小结：刚才我们从图中找到了条件、问题和数量之间的关系，顺利地解决了问题。

认知心理学认为：新的学习是在原有学习根基上产生的，新的知识总是通过与学生原有认知结构中相关知识相互联系和作用后获得意义的。在课堂教学中，我利用学生已有的学习经验正视学生的学习起点，设置前置性练习，勾起学生对画图的记忆，为新知学习做好必要的铺垫，例1中，通过让学生自主审题，整理条件和问题或让学生对直接列式解答的理解，使他们意识到面对多而复杂的信心，应该运用某种方法、策略整理信息以帮助我们更快地看懂题目，这时画图策略的选择自然成了学生的内在需求。

二、数学思想方法的渗透

数学思想是数学的灵魂，数无形时少直觉，形无数时难入微，本课内容画图策略是数形结合思想的重要体现，本课之前，学生已经积累不少画图的具体经验，不过以前画图目的是使题目更直观和形象，今天画图策略的作用是帮助分析数量关系，确定解决问题的思路，找到解决问题的有效方法，从一开始引导学生把题目中相应的问题和信息在图上标出来，把抽象化的文字、形式化的数据逐步转化成形象的图形，帮助学生理清条件和问题之间的关系，最后在计算过程中让学生指着示意图说出每一步的思路等，有效发挥形象思维和抽象思维的协同作用，使学生在潜移默化中感受数形结合的思想，体会策略的价值。

三、加强数学知识的整体联系

环节2：学习新知后回顾相关知识。

师：其实画图对我们来说并不陌生，在以前学习内容中已经悄然存在了。

图1：师：课一开始的这两题，我们借助图形看清楚了其中的条件、数量之间的关系。

图2：（先圈出来）问：你能说说苹果和梨之间的关系吗？

师：我们以前就是借助图一知道了之间的倍数关系。

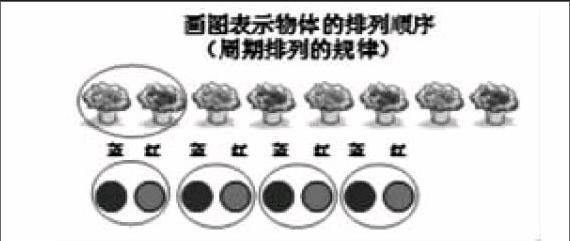
图3：问：这是什么现象？（周期现象中的规律）你是怎么找到其中规律的？

师：借助图形通过圈一圈，我们很快找到了规律。

数学是一个有机整体，各知识之间相互联系，教师要引导学生关注知识的生长点和延伸点，把每堂课教学知识置于整体知识体系中，注重知识的结构和体系，处理好局部和整体的关系，引导学生感受数学知识的整体性。

四、拓展和变式，引发认知冲突，形成有效联结，提升思维能力

教育心理学认为：在学生内部认知结构中，刚获取的知识点与整个系统的联系还处于松散状态，在这些新知识点之间并未形成有效联结，只有通过知识之间的相互碰撞，引发出能暴露问题本质的各种信息数据，再由学生自主完成信息数据的收集、整理、分析，把问题本质反映出来，才能实现知识之间的有效联通。

环节3：拓展和变式。