从混凝土历史发展长河中学习理解A定则B公式之三

王永逵，王健，耿加会，余春荣，冯立艳

（1.上海奇齐科技开发公司，上海　201600；2.河南舞阳县惠达公路工程公司，河南　舞阳　462400；3.建筑材料工业技术情报研究所，北京　100024；4.四川德阳明鸿商品混凝土有限公司，四川　德阳　618099）

从混凝土历史发展长河中学习理解A定则B公式之三

王永逵1，王健1，耿加会2，余春荣3，冯立艳4

（1.上海奇齐科技开发公司，上海201600；2.河南舞阳县惠达公路工程公司，河南舞阳462400；3.建筑材料工业技术情报研究所，北京100024；4.四川德阳明鸿商品混凝土有限公司，四川德阳618099）

人的认识在不断实践中，从未停止在一个平面上，并力图以新的认识指导混凝土技术的发展。上世纪的40年代后，随着水泥工业和混凝土技术的发展，人们发现水泥标号或强度不同，也应是混凝土抗压强度不可忽视的另一重要影响因素。90年代后随着对混凝土耐久性的重视，矿物掺合料的普遍应用，人们总是力图以新的形式对混凝土强度做新的表达。这是B公式发展演变的必然规律，没有改变的是对随机变量的数理统计原理。

水泥强度；强度等级；矿物掺合料；发展与演变；高效减水剂

1　保罗米公式的演变与发展

1.1在 B 公式中引入水泥标号

早在1955年我国混凝土技术的奠基人，前工程院资深院士吴中伟先生，在撰写的《混凝土配合比简易法》[1]一文中认为，“混凝土的强度和其它性能﹙如耐久性﹚是灰水比和水泥标号的函数，灰水比愈大，强度愈高”并以式（1）表示。

混凝土强度：

式中：

Rη——为水泥强度等级。

我国1985年6月出版的电视大学教材《建筑材料》[2]，也指明混凝土强度应与水泥强度等级（Rc）和灰水比成正比关系。

式中：

Rc一为水泥强度等级；

A，B ——为回归方程式系数。

湖南省高速公路公司的苏格兰1999年5月撰写的《法国混凝土配合比设计方法及应用》[3]一文中介绍，法国水泥混凝土配合比设计中的强度计算理论，除强调继承了 B 公式的模式外，也引入的是水泥强度等级，而不是水泥的实测强度，其公式为∶

式中：

σ28′——为28d 的混凝土设计抗压强度， 计算时考虑1.15的强度系数，MPa。

σc'——水泥强度等级，MPa；

G ——骨料参数；

C ——水泥用量，kg/m3；

E ——用水量， kg/m3。

在 B 公式中引入水泥强度等级或实测强度，两者的意义是不同的。水泥强度等级是确定性数据，是事先可以控制或精确量测的普通变量。而水泥的28d 实测强度在进行配合比设计时，谁也不知道是多大。以我国P·O42.5为例 ，它可以是43.0～52.0MPa 之间的任何值，是一个连续型随机变量。我国现阶段在普通商品混凝土生产中普遍使用的是 P·O42.5水泥，而 P·O52.5水泥很少用，使用 P·O62.5和 P·C32.5强度等级的水泥甚是罕见。本文之二（II）中拟合的 B 公式（26）（下文称作式2-26），就是以现阶段普遍使用 P·O42.5水泥而积累的自变量（xi）和因变量（yi）数据拟合出来的。在原有B公式中引入水泥强度等级，可估算变换水泥强度等级或水泥強度等级时对 C/W 或强度的影响，但此引入水泥强度等级后的公式，对采用 P·O42.5水泥无实际意义。这是因为 B 公式本身就是广泛使用 P·O42.5水泥拟合的，再引入水泥强度等级的公式是重复因子，已失去独立因子的意义，而对不同标号（强度等级）的水泥还是有实际意义的。

1.1.1在 B 公式中引入常用的 P·O42.5水泥

在B公式中引入水泥强度等级的方法，应在原有普遍使用 P·O42.5水泥统计得到的式2-26的基础上，以原有 K0＝-19.324，K1＝26.529，用等量取代的方法引入水泥强度等级后的B公式，只是变换了两新的回归系数， 仍为一元线性回归方程。原有的两回归系数 K1，K0转换成 A1和 A0如下：

则B 公式2-26变换为：

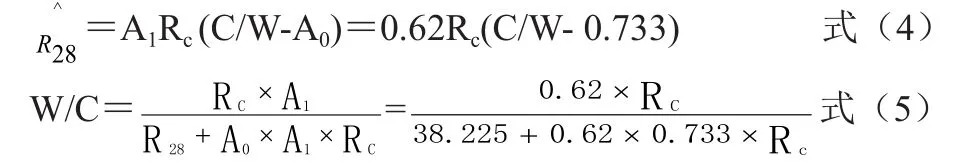
用本文之二中的3.2章节 C30实例，试用 P·O42.5水泥，估算和 W/C。

（2）已知：C30混凝土水胶比 W/C＝0.46，用式（4）估算 C30混凝土28d 抗压强度

结果表明都与本文之二中的3.2的用 C30混凝土实例中计算结果相同。说明：式2-26和式2-27本来就是在我国现阶段普遍使用 P·O42.5基础上拟合的，现在式（5）中仍引入的 Rc是 P·O42.5，是重复因子，无实际意义，与式2-26和式2-27计算的，无论是水灰比或混凝土28d 强度完全相同是不奇怪的。再引入 Rc只是变换了两回归系数。但对生产中采用不同水泥强度等级时，就会发现混凝土强度和灰水比会随水泥强度等级的升降而升降，其升降的变化规律是给予应关注，试看以下计算：

1.1.1仍以本文之二3.2中的 C30为例，用 P·O52.5水泥时，和 W/C的计算

（1）保持原水灰比 W/C＝0.46，即灰水比 C/W＝2.174不变，代入式（4）计算 ：

计算结果表明原水胶比不变， 与水泥强度等级有近似正比关系，达到接近提高两个强度等级接近 C40配制强度的水平，效果相当显著。

结果表明用 P·O52.5水泥配制 C30混凝土时，保持原水灰比（0.46）不变，混凝土 R28显著提高， 与水泥强度等级有正比关系，增强效果显著；保持 C30配制强度不变，混凝土的水灰比只是随水泥强度等级增大而提高，但两者没有比例关系，0.52≠0.46×(52.5/42.5)＝0.57。但是表明提高水泥强度等级对配制高强度混凝土时，水灰比可相对地放宽，会给生产带来显著的方便。

1.1.2仍以本文之二中的3.2C30为例，用 P·C32.5水泥，估算和 W/C

（1）用 P·C32.5水泥的灰水比 C/W＝0.46保持不变的估算。 已知原灰水比 C/W＝2.174，代入式（4）

说明水灰比不变，混凝土强度随水泥强度等级降低而降低，并近似成正比关系，将达不到 C30混凝土的配制要求。如满足配制强度要求，必须将水胶比降低。

（2）用 P·O32.5水泥配制 C30混凝土的水灰比估算

说明用32.5水泥配制 C30混凝土只要适当降低水灰（胶）比，完全可生产出合格的优质混凝土。这在缺乏矿物掺合料的偏远地区生产优质混凝土，无异是一个可行的方法，只是需将原0.46的水灰比降到0.38就可以了。水泥强度等级与混凝土配制强度等级的与灰﹙胶﹚水比成正比，与水胶比只是随有水泥强度等级的降低而降低，但并没有严格的反比关系（反比为0.35）。W/C＝0.38是一个略小于或接近原用 P·O42.5水泥配制 C40混凝土的水胶比（0.39）。

说明B公式中代入不同的水泥强度等级（强度等级）还是有明显的意义的，对胶水比（水胶比）和估计值有显著的影响。在没有适当矿物掺合料的偏远地区，有了高效减水剂，采用 P·C32.5复合水泥也可配制生产合格的混凝土，掺不掺矿物掺合料不是现代混凝土的必要条件。了解这一规律在生产中对调整配合比是很有用的。

2　在 B 公式中引入水泥28d 实测强度 fce的演变

在保罗米公式中引入水泥28d 实测强度，是B公式中引入水泥强度等级后的又一个发展。60年代初前苏联的专家来华讲学时，介绍了他们为考虑水泥强度不同对混凝土强度和水灰比计算的影响，而将 B 公式改造成下式（6）的形式[4]：

式中：

fcu,o——混凝土28d 强度期望值，MPa；

fce——混凝土28d 实测强度，MPa；

αa，αb——两回归系数。

这一改变为我国编制《普通混凝土配合比设计规程》以来较早釆用，一直沿用到 JGJ55－2000“规程”，并较为广泛的被纳入我国各有关专业的高校教科书影响深远。“规程” 推荐回归系数如表1所示。

表1　J GJ55一2000“规程” 推荐回归系数

“规程” 所推荐的包罗米公式（6），是以大量塑性混凝土试验基础上采集样本（Xi，Yi），通过最小二乘法一元线性回归而成的。以笔者对回归分析的学习理解，它应该只适用于塑性混凝土 fcu,o和 W/C 的期望值估算，因釆集样本的原因，本来就不适用于当时已经在蓬勃发展的大流动商品混凝土。当时在商品混凝土生产中应用式（6）和式 （7）出现较大的偏差，应该是很正常的。不同质的问题应该用不同的方法去解决，世上不存在放之四海而皆准的真理。B 公式应用场合与样本数据的釆集范围有不可回避的直接关系。本文之（一）表1中以 C30为例，美国标准 ACI211.1推荐的配合比设计引气型与非引气混凝土的W/B（0.45与0.54）差别之大，足以说明这一问题。但在同一类型的混凝土配合比设计中用式（7）计算 C15～C50与ACI211.1非引气混凝土推荐的 W/C 比较，两者还是很相近的，且很有规律性。如表2。

表2　“规程”计算 W/C 与 ACI211.1推荐 W/C 的对比

两者执行的年代相近，标准条件相似，应具有一定的可比性。它们间的少许差别，与样本取自不同国家、原材料和标准的差异以及本来 A 定则 B 公式就是近似关系有关。这种同一设计强度的 W/C 相似性不是偶然的巧合，是不确定数据运算法则和生产实际的客观反映，说明我国的 JGJ55－2000“规程”推荐的碎石混凝土 B 公式用于塑性混凝土是可信的。可是在过去的年代这是一个广受争议的问题。这一问题的误判，说明了“混凝土界的科技人员应该具有必要的数理统计知识”，否则将可能导致无意义的争执。其次，ACI211.1有关混凝土配合比设计时，W/C 的选择不是按碎石、卵石分类，而是按引气型与非引气型分类，这对我国今后标准的修订，也是值得参考的。

2.1引入水泥实测强度在现代混凝土中的应用

在数理统计中，B 公式中引入水泥28d 实测强度与引入水泥强度等级的数据性质是不同的，后者是确定性数据，而水泥28d 实测强度是一连续型随机变量。它的实测值在生产和配合比设计时无法事先控制和量测的。以 P·O42.5水泥为例，一般可在43～52MPa 之间波动。利用式（6）和式（7）估算混凝土强度和水灰比，不能用一个随机变量去估算另一个随机变量。JGJ55－2000“规程” 是如何解决这一问题的未见介绍。对现代大流动多组分混凝土如何拟合 B 公式，笔者设想可以的采取变连续型随机变量为水泥28d 强度平均值，即变随机变量为确定性变量的方法，，仍以等量取代的方法代入式2-26，不必将水泥实测强度作为除 W/C 以外的另一自变量进行二元线型回归的公式拟合。原因是在式2-26的公式拟合中，因变量（Y）水泥实测强度，已在每个子样 yi中得到直接反映，再在拟合 B 公式作为另一个自变量，将是重复的、无效的。直接将代入式2-26，可得到比用水泥强度等级更为细致估算 R28和水灰比的 B 公式表达式，用以反映水泥实测强度对混凝土强度和水灰比估算的影响。

以笔者十几年来在几个省市商品混凝土生产一线的统计，现阶段广泛采用的 P·O42.5水泥的平均实测强度约为48.0MPa，可用此值代入式2-26中，建立式（8）和式（9），其结果也只是改变回归方程的两系数 ， 项，在方法上与代入水泥强度等级（Rc）类似。具体方法如下：

式中：

fcu,o——混凝土配制强度值，MPa；

fce——水泥实测强度，MPa；

αa，αb——两回归系数，αa＝0.55，αb＝0.732。

（1）以本文之二中的3.4C30为例，用 P·O42.5的平均值估算和 W/C。

已知：C30混凝土配合比胶水比 B/W＝2.174，用式2-26估算 C30的配制强度 fcu,o＝38.2MPa

①用 P·O42.5水泥28天强度平均值，估算 C30混凝土强度：

与用式2-26估算的38.2MPa 两者基本相等，与 B 公式相比没质的变化。

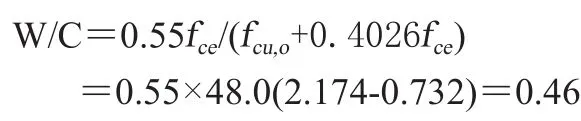
②用 P·O42.5水泥28天强度平均值，估算配制 C30混凝土水灰比（W/C）说明用式（8）和式（9）与用式2-26和式2-27估算C30混凝土强度和水灰比与用 B 公式没有两样，只是改变两回归系数。

（2）以 C30为例，当水泥实测强度在 fce＝43～52MPa之间波动时，计算对混凝土抗压强度和水胶比影响

这是一种最常见的状况，变是绝对的，不变是相对的，即使是同一个水泥厂，原材料和工艺不变，水泥实测强度也不会完全相同。有了上面用水泥的28天强度平均值48.0MPa）建立了式（8）和式（9），再估算水泥实测强度的和 W/C就变得很简单了。只需把 fce的实测值代入式（8）和式（9）即可。fce＝44～52MPa 之间的波动，其波动大小与水泥厂管理水平有关，且服从正态分布。弄清因水泥实测强度波动对混凝土抗压强度和水胶比影响是很有实际意义的，见表3数据。

表3　P·O42.5水泥强度波动对 C30混凝土水胶比和抗压强度影响

由表3数据可以说明：

（1）若配制强度一定，混凝土的水灰（胶）比随水泥强度而增加，灰（胶）水比随水泥强度提高而减小，从而确立了水泥实测强度是配合比中水灰（胶）比选择的重要参数；另外，从表3中可看出，配合比设计中的水灰比并非确定值，以 C30为例，由于水泥实测强度的波动，水灰比（W/ C）可以在0.426～0.482之间变化，而0.46只是一个平均值；在水灰比一定，如 W/C＝0.46时，因水泥实测强度的波动可使 C30混凝土强度在34.1～41.8MPa 波动，它们都是随机变量，且应服从正态分布。因之，控制进厂水泥质量对确保混凝土质量有重要意义。

（2）灰（胶）水比一定混凝土的实测强度与水泥的实际强度有正比关系；

（3）在配合比设计与试验中，由于水泥的实际强度是未知数，混凝土的28d 强度估计值和合理水胶比实际上是算不出来的，可取投入试验前的估计值（如 P·O42.5×1.16），或结合已往自己常用水泥的平均强度作相应调整，真正能满足95% 保证率的水胶比，是靠试验结果最终决定。

（4）用式（8）估算不同强度等级的水灰比与 C20～C50的实际生产常用的基本一致，而 C10～C15、C55～C60有一定的略有偏差，这是由于 B 公式把本来属于双曲线的试验线型简化成直线的结果。对常用的水泥一般偏差都较小（在0.01～0.02）。了解这一规律，在试配中作适当调整即可，本来只是估算值，无须像某些专家提出的将胶水比—强度直线分成三阶段[10]。

但在实际生产中，对不同工程要求和不同的原材料品质，没有一成不变的水胶比，也没有一成不变的配合比。必须依据原材料的具体技术性质和工程实际参照公式（8）和表3，除对初步选择的水胶比（W/B）试配外，按三点法根据28d 强度试验结果，选最接近配制强度的那个水胶比做最后决定。设想靠本本上记下的几个配合比或只是靠以往的经验“吃遍天下”是要碰壁的。

2.2用 P·O52.5的水泥配制 C30，水泥实测强度对混凝土估算和 W/C的影响

（1）已知 P·O52.5水泥实测强度 fce在53～62MPa 之间波动，代入式（8）和式（9），试估算 C30混凝土的和 W/C。

表4　P·O52.5水泥实测强度波动对 C30水胶比和抗压强度的影响

表4计算结果表明：

（1）保持 C30配制强度不变，水胶比随 P·O52.5水泥实测强度增加而增大；胶水比随 P·O52.5水泥实测强度增加而显著降低；

（2）保持原 C30水胶比不变，混凝土强度与水泥强度成正比，可用 P·O52.5水泥配制出 ＞C40的混凝土，水胶比可提高两个等级以上。表明配制高强度混凝土用 P·O52.5水泥，可带来显著的方便。

2.3用 P·O52.5配制高强度等级混凝土估计其水胶比

在商品混凝土生产中，习惯把 C10～C20；C30～C45；C50～C60分别称之为低强度等级、中强度等级和高强度等级。用 P·O52.5水泥配制中、低强度等级的很少，而用P·O52.5水泥配制高强度等级混凝土者常有之。试以 P·O52.5水泥实测强度估计值 fce＝52.5×1.15＝60.4MPa，估算 C50、 C55、C60的水胶比和可能达到的，见表5。

表5　P·O52.5水泥配制 C50、C55、C60的水胶比和

表5　P·O52.5水泥配制 C50、C55、C60的水胶比和

混凝土强度等级C50C55C60C80配制强度 (MPa)59.964.969　　88用 P·O52.5水泥式（9）估算 W/B0.390.370.360.29用式（8）估算 （MPa）60.765.368.0　91.52用 P·O42.5水泥式（9）估算 W/B0.330.310.290.25

表5结果显示用 P·O52.5水泥配制高等级强度商品混凝土，水胶比与用 P·O42.5水泥约可提高两个等级以上，给生产带来显著的方便，并且对一般混凝土公司，在原材料选择上注意，配制 C80要求水灰（胶）比＜0.29，只要具备配制C80高强混凝土所要求的优质砂石等原材料，在掺用高效减水剂的条件下也不是难事。另外，笔者认为：即使用 P·O52.5水泥配制中等强度商品混凝土，在矿物掺合料供应不短缺的地区也是经济合算的。这样可减少水泥厂生产 P·O.42.5水泥掺入那部分混合材的重复运输费用，并有利于节能减排。

2.4用 P·C32.5水泥配制本文之二中3.2C30配合比混凝土，预测其 W/B 和抗压强度

用 P·C32.5水泥强度波动对 C30混凝土抗压强度和水胶比影响试验数据详见表6。由表6可知：

（1）用P·C32.5水泥配制 C30混凝土要依据实测强度，降低水胶比，这在普遍使用高效减水剂的今天完全是可能的；

（2）保持P·C32.5配制 C30的水胶比0.46不变， 不可能配制出满足95% 合格的 C30混凝土，必须依据水泥的实测强度降低水胶比；

（3）有了高效减水剂的帮助，用 P·C32.5水泥不必另掺矿物细粉料，可配制出 C30～C50的优质混凝土是可能的，在没有矿物掺合料的偏远地区，不失为一种较好的选择。

表6　P·C32.5水泥实测强度波动对 C30抗压强度和水胶比的影响

3　A 定则 B 公式在现代混凝土中新的发展和演变

3.1保罗米公式在现代混凝土中新的演变的探讨

进入上世纪90年代后，混凝土耐久性和可持续发展问题引起人们的广泛关注，从而普遍掺用矿物掺合料成为现代混凝土的重要标志之一。B公式在现代混凝土中的应用随掺用矿物掺合料对胶凝材料强度的影响，而尝试以新的形式反应这一变化。为此在 JGJ55－2011“规程”[5]编制中以胶凝材料强度代替原来的水泥28d 实测强度，并引入了掺合料影响系数（γf）对 JGJ55－2000的式（7）、式（8）作了新的表述，这是 B 公式应用上在新的条件下一个新的尝试。表述如下：

式中：

αa，αb——为常数项，在使用碎石时 αa＝0.52，αb＝0.2；

fb——胶凝材料强度，fb=γfγsfce；

γf和 γs——分别为粉煤灰和高炉矿渣粉影响系数。

掺合料影响系数（γf、γs）的引入给此条件下的常数项αa、αb的确定带来新的问题。原因是 fce和 γf、γs的取值都是随机变量，从数学关系上在此状况下，αa、αb不可能保持常数。即使以常用水泥 P·O42.5的平均强度代入，在 γf和 γs技术性能、掺量、组合方式都是随机变量的条件下，αa、αb两回归系数也难以保持为常数项。JGJ55－2011“规程” 解决这一数学问题的办法未见介绍，只是给出了（表7）γf和 γs的取值范围[5]。

表7　粉煤灰和高炉矿渣粉影响系数的取值范围

笔者也试用表7矿物掺合料的推荐值，对 C10～C60普通商品混凝土常用配合比进行检验，在规定的范围内试选γf、γs值，可得到与生产实践中统计 W/C 基本一致的结果，只是在 C55和 C60时有一定的差异（见表8）。而混凝土28d预测强度值 C10～C60可以在推荐的 、 范围内，用式（10）和式（11）都能得到较为接近配制强度的值，这一点还是很难得的。笔者认为“规程” 的编制不失为一个伟大的尝试，只是还有待进一步完善。

表8　C10～C60水胶比和的估计值计算

表8　C10～C60水胶比和的估计值计算

0.70/16.650.55/24.150.46/37.90.37/49.20.33/67.10.32/65.9按 B 公式大本文之二式（27）计算 W/B0.730.570.460.390.330.31《商品混凝土》03年3期王元从实用际生产的统计值－0.570.460.380.33＜0.31混凝土强度等级C10C20C30C40C50C60粉煤灰掺量(%)50～5530～4020～3015～2510～2010～15高炉矿渣粉掺量(%)－1011141517γf/γs取值0.53/1.00.58/1.00.77/1.00.78/1.00.95/1.01.0/095按 JGJ55－2011“规程”估算 W/B和预测 R28

但因在生产实践中矿物掺合料的品种、活性、掺量以双掺时的组合比都非确定值的随机变量。按“规程”表7推荐的影响系数的取值，也有较大幅度的变化。以本文之二3.2C30实例：高炉矿渣粉掺量10%，γs＝1.0是无疑义的，但粉煤灰掺量为26%，γf为可在0.69～0.79之间随意取值，在0.01的数位上有10个数可取，具体是多大不知道。表8中的选择 γf＝0.77，是笔者在0.69～0.79之间逐个试算确定下的，这就带来取值的不确定性。在利用式（10）和式（11）估算fcu,o或 W/C，用 γf和 γs两个随机变量去推算另两个随机变量，必然给应用也带来困难，给应用也带来困难，必须通过逐个试算才找到与实际生产中统计的接近的水胶比和混凝土强度估计值。这对科研和生产中配合比的拟定初选水胶比带来很大的盲目性。

另有在本文之一前言中有“作者”[8]提到的－个 C35工程实例，对2011“规程”提出疑议的原因就在于此。该工程的 C35配制强度 fcu,o=43.225MPa，配合比中水泥为 P·O42.5实测强度 fcu,o＝50.0MPa，Ⅱ 级粉煤灰掺量45%，S95矿粉10%，W/B 取0.42，R28实测达45MPa。以此工程实例如按“规程”表7推荐的矿物掺合料影响系数的取值， γf＝0.55，γs＝1.0，代入“规程”式（11）：

这显然与实际所用的 W/B＝0.42出入很大，“规程”引入的矿物掺合料影响系数，试图把不同的矿物掺合料影响因素都考虑进去，用意虽好，不仅没有给初学配合比设计的人提供方便的办法，也不符合数理统计的运算法则。这是“规程”编写前进中的问题，提出来供参考。

3.2对这一问题的建议

笔者认为，在现代混凝土中掺用的矿物掺合料多样性、复杂性的情况下，无法具体用影响系数考虑其影响，在“规程”编写的 B 公式中可不急于引入影响系数（γf、γs），它不同于水泥强度等级和水泥实测强度，是更复杂的随机变量。B 公式的演变和发展暂保持引入水泥实测强度的式（8）、式（9）形式即可。矿物掺合料、外加剂等诸多的影响皆“隐藏”于因变量“Yi”中，并非忽视其影响。现代混凝土配合比设计中如何考虑高效减水剂和矿物掺合料的影响，应遵循数理统计的原理。回归分析的方法，就是建立在大量可量测、可控的胶水比自变量 Xi和因变量 Yi的基础上，利用最小二乘法原理，通过回归分析拟合的 A 定则—B 公式，已知胶水比 B/W 估算，或已知 fcu,o估算 W/C。在 B 公式的发展演变中虽引入了水泥的28天实测强度 fce也是在根据以往累积数据，已知 fce的基础上估算和 W/C。在 B 公式应用中不能用一个随机变量去估算另一个随机变量。

本文（一）中作者试配的 C35[11]混凝土 W/B 取0.42，与笔者在本文之二的公式（27）计算的水胶比（本文之二表6）相同，也与王元的调查统计一致。

考虑水泥实测强度用式（8）估算“作者”试配时应达到的混凝土强度：与“作者”用水胶比0.42达到的混凝土试配强度 fcu,o＝45.1MPa 基本一致。实际上如用“作者”试配时水泥实测强度50MPa 估算此 C35的配合比设计中需要的水胶比：

结果说明，不必用0.42，只需0.44，就可达到 C35配合比满足强度95% 保证率的要求。当然，作者也可用0.42的水胶比，只是保证率更高些。

另外，“作者”拟定的这一 C35配合比可能是用于降低水化热的缓凝型大体积基础筏板混凝土或用于减少混凝土自收缩的高墙、长墙、薄壁结构，应属于特种混凝土或高性能混凝土一类。这一点也颇有启示，表明大掺量矿物掺合料的混凝土 B 公式可不必另拟引入掺矿物掺合料系数的，直接用式（8）、式（9）即可得到符合工程实践的结果。这是由于式（8）拟合时，自变量 W(Xi) 和因变量 (Yi) 取自广泛使用大掺量矿物掺合料的现代混凝土，利用式（8）计算混凝土强度期望值与实际一致的结果是不奇怪的。实践证明引入水泥实测强度的 B 公式仍可用于现代混凝土的合理性。相反，由于引入矿物掺合料影响系数属随机变量，很难选准 γf和 γs的确定值，不是更接近实际，而是渐行渐远。

“规程”编写的作用是给初进入混凝土技术工作的人员，给予进行配合比设计的基本原理、原则和方法、步骤，从而得到试配时水胶比估计值，并依此 ±0.05分别计算出水泥、砂、石用量的三个配合比，最后从得到的两段水胶比－混凝土强度值的折线，用内插法找到最接近配制强的水胶比。有实践经验混凝土技术工作的人员在进行配合比设计时，多是根据经验用类比法初步拟定水胶比进行混凝土试配，但28d 混凝土试配强度必须 fcu,o≥fcu,k+1.645σ，如低于fcu,o须适当调低水胶比。

“规程” 充其量只能给出根据全国范围采集的样本（xi，yi）拟出的 B 公式，根据此 B 公式估算的水胶比，也只是全国范围的平均值，虽有重要参考价值，但不一定贴合每个混凝土公司实际，更不能适用于所有的混凝土品种。式（8）和式（9）是基于当前较普遍使用的单掺或双掺粉煤灰、矿渣粉的商品混凝土生产统计得到的，它用于塑性或干硬性混凝土也会有较大的误差。真正贴合实际的是靠自己积累的数据，导出符合自己实际 B 公式的 αa、αb值。不能全靠“规程”。对于一个关系国家基本建设的混凝土行业，没有“规程” 是绝对不行的，它的任务是根据一个阶段混凝土技术的发展水平，针对混凝土的配合比设计给出依据的基本理论和方法、步骤以及平均水平的参考。但“规程”不能完美解答所有的问题，能担负的任务是有限度的。

4　从不同国度，不同年代样本建立 B 公式中的启示

（1）依据上世纪70年代的英国的一组塑性混凝土水灰比一强度数据[6]（表9）拟合的 B 公式。

表9　上世纪70年代英国的四组份塑性混凝土[8]

上世纪70年代的英国的混凝土灰水比一强度数学模型图1。

用式（14）估算混凝土强度等级 C30的 W/B：

图1　上世纪70年代的英国的混凝土灰水比—强度数学模型

（2）我国上世纪80年代（四组分塑性混凝土）一组胶水比—强度数据[3]（表10）拟合的 B 公式。

根据表10灰水比—强度数据电脑拟合的 B 公式：

用式（17）估算混凝土强度等级 C30的 W/B：

表10　上世纪80年 代灰水比一强度数据

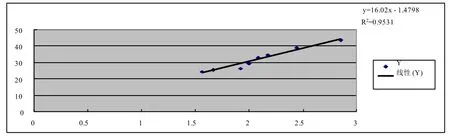
图2　80年代的我国的混凝土灰水比—强度数学模型

（3）已知现代多组份大流动性混凝土的强度—胶水比公式，用公式估算混凝土强度等级 C30的W/B：

用上述不同国度与年代混凝土的 B 公式计算 C10～C50的 W/B，见表11。

表11　上世纪80年代的 B 公式估算 C20～C50的水胶比

上述结果表明：

（1）不同国度、不同年代、不同的强度水灰比公式表明，改变的只是 B 公式的两常数项，而保罗米米公式表达的在标准条件下，“对给定原材料，混凝土强度与灰水比可近似成正比” 的关系没变，变的仅是两回归系数。

（2）用我国80年代塑性混凝土与英国70年代塑性混凝土的 C30水灰比相比，当时我国 C30混凝土的水灰比要低到0.40，同样的抗压强度等级英国的水灰几只要0.48就可以了。说明当时我国的常用水泥活性似乎比英国的水泥低的多，这可能与当时科技发达国家多用纯硅水泥有关。

（3）从80年代混凝土 B 公式（17）与现代混凝土的式2-27C30的W/B（0.404∶0.46）比较，表明早些年四组混凝土强度较低，C40混凝土已是高强混凝土了，生产 C50水灰比要低到0.26，在当时高效减水剂还很少使用的情况下几乎不可能，平均强度也就是在 C25上下，进一步提高强度是困难的。同时，还表明改革开放以来，高效减水剂的发展与应用，使混凝土的技术进步有了很大的变化。现在不仅能在一般条件下生产从 C10～C60的大流动性混凝土，而且生产 C80混凝土已不是难事。现在 C30混凝土的水胶比只需要0.46就可以了，且可为大流动性可泵送混凝土，更适应当前基本建设高速发展的需要。

（4）现代混凝土与上世纪混凝土技术水平相比，事实表明：高效减水剂的发明，具有里程碑的意义，使混凝土技术发生质的飞跃，影响是巨大的。

5　高效减水剂对 B 公式的影响

高效减水剂是一种表面活性剂对水泥有打开絮凝结构，分散、渗透作用， 增加与水的接触面，加速水化；并且多为复合型高效减水剂，从来就不只是单纯的减水作用。以一般萘系高效减水剂而言，在成分中合成工艺带来的硫酸钠常在8%～12%。无水硫酸钠是一种典型的早强剂，对混凝土早期和后期强度都有明显的增强作用，它不可能对强度没影响。它的影响主要表现在对 B 公式中两回归系数 αa、αb的大小，而 A 定则－B 公式所表达的在标准条件下“对给定的原材料，强度只决定于水胶比一个因素”的论断没有变化。

6　结束语

（1）历史是现实的源头，回顾历史是为了更好地了解现在展望将来，不忘记历史的民族是有希望的民族。在五千多年来混凝土历史发展的长河中，混凝土的技术发展是漫长的、绶慢的，有时甚至会倒退，但总是在前进，人们在生产生活实践中总是会有新的发现发明，对自然王国的认识永远不会停止在一个平面上。混凝土世界是物质的、有规律的运动，或早或晚总可为人们所不断加深认识，那种只能是瞎子摸象的看法是不符合辩证法的。

（2）在混凝土技术发展中始终离不开“数”，科技活动中更是强调用“数据说话”，明确“数据”的性质很重要。对“非确定性数据”的运算，只能是期望值的估计值平均值，充其量是出现机率最大的值，认识这一点十分重要。从事混凝土行业的科技人员，必须具有数理统计知识，从区分“数” 的性质上的不同，去寻求合理的解决方法，否则你的认识会产生误判，甚至看不懂别人的文章。

（3）从1896年费雷特建立了著名的普适公式；到1918年美国伊利诺斯大学的达夫·阿勃莱姆斯建立的非线回归方程A定则，再到1930年瑞典科学家的保罗米建立一元线性回归称为 B 公式，直到在 B 公式基础上引入水泥实测强度，都是在实践中对不确定性数据运算的认识的一种发展演变，随着混凝土技术的发展，还会有更反映实际的新的表达式，认识永远不会停止在一个水平上。

（4）在现代混凝土普遍使用高效减水剂和矿物掺合料的今天，对 A 定则 B 公式的影响，主要表现在相应的两回归系数，对A定则 B 公式的各自数学关系没有变化。

（5）此文的编写过程也是笔者的重新学习过程，因涉及“规程”，为慎重起见曾请教过母校西南交大的高芳清教授和兰州交大的一些教授等，编辑部荣誉主编的丁老等他们都曾给过一些指点帮助，对笔者很有启发，在此表示深深的谢意。但有些建议并未完全接受，好在写出来了文责自负，对的与他们帮助指点分不开，错的是由于笔者的水平有限，重在参与，全当信口胡说，有不妥之处，盼高人指点，从不同观点的争论中，再进一步学习有关问题，那也是很好的事。

（完）

[1] 吴中伟．混凝土配合比筒易设计法[N]．土木工程学报，1955,12．

[2] 建筑材料，王世芳主编．北京：中央广播电视大学出版社出版，1996．

[3] 苏格兰．法国混凝土配合比设计方法及其应用[J]，国外公路，1999(5)：48-53.

[4] [加]西德尼·明德斯，[美] J·弗朗西期·杨，[美]戴维·达尔文．吴科如，张雄，姚武，等译．北京：化工出版社，2005,1．

[5] JGJ55－2000．普通混凝土配合比设计[S]．

[6] JGJ55－2011．普通混凝土配合比设计[S]

[7] 马克思主义基本原理概沦[M]．北京：高等教育出版社，2009．

[8] 梁文泉．保罗米公式还能用来确定现代混凝土的水胶比吗？[J]．商品混凝土，2013(3)：5-7．

[9] 王永逵，陆吉祥，著．材料试验与质量管理的数学方法[M]．北京：中国铁道出版社，1990．

[10] 杨文科．现代混凝土科学的问题与研究[M]．北京：清华大学出版，2015,5．

［通讯地址］上海松江区荣乐中路228弄北九峰小区152号302室（201600）

王永逵（1934—），前兰州铁道学院土木系建材室主任。