电磁测深数据地形影响的快速校正

薛国强， 闫述， 陈卫营

1 中国科学院矿产资源研究重点实验室， 中国科学院地质与地球物理研究所， 北京 100029 2 江苏大学计算机科学与通信工程学院， 江苏镇江 212013



电磁测深数据地形影响的快速校正

薛国强1， 闫述2， 陈卫营1

1 中国科学院矿产资源研究重点实验室， 中国科学院地质与地球物理研究所， 北京 100029 2 江苏大学计算机科学与通信工程学院， 江苏镇江 212013

地形起伏会对电磁法的数据产生一定影响，尤其会影响浅部地层电性结果的准确性.本文通过对地形影响基本规律、经典比值校正原理的分析, 认为可以用实测标准电阻率替代数值模拟中均匀半空间电阻率，提出一种新的地形影响快速校正方法，即采用小极矩直流电阻率法获得无地形影响的表层电阻率值，作为地形校正的标准电阻率，以此构造一个新的校正公式.分别对CSAMT和TEM仿真和实际测量资料进行地形校正处理，效果较好.说明新的比值校正公式，是一种快速、有效和实用的校正算法.

电磁法； 地形影响； 校正； CSAMT； TEM

1 引言

在山地电磁法勘探中，地形起伏不仅使观测点偏离水平位置，还使大地中电磁场的分布发生变化，导致观测数据中包含了目标体异常和地形异常，对推断解释造成干扰(Jiracek G R，1990；王绪本等, 1999；Hördt and Scholl，2004；Tang et al.，2011).消弱地形影响，是提高山地勘探精度、取得良好地质效果的关键问题之一.地形影响解决方案中，经典的方法是比值校正法(李金铭，2005)，该方法先通过一定手段获得纯地形异常，然后用地形造成的异常倍数乘或除以实测数据达到消弱地形影响的效果.在早期，获得纯地形异常的手段有水槽、土槽、导电纸等物理模拟方法，直流电法还可利用场的解析解通过保角变换获得.随着计算机和计算技术的发展，二维和三维纯地形正演模拟成为获得纯地形异常的主要方式(Wannamaker et al., 1986; Leppin, 1992; 闫述等, 1996; Xu and Zhou, 1997; 孙怀凤等, 2013).进一步地，将地形作为二维、三维地质构造的组成部分代入反演也取得了大量的研究成果(Tong and Yang,1990；Yi et al., 2001；吴小平, 2005；肖怀宇, 2006；Haber et al., 2007；雷达, 2010；刘云, 2012；Yang and Oldenburg, 2012；董浩等；2014).二维、三维纯地形影响正演和带地形的反演具有强大的仿真能力，但对计算机内存容量和速度要求极高.在人工源野外勘探中，除必要的点位测量外，发收之间及周边的广大区域还须有相当密度的测地工作.因此，在数值正反演向实用化发展的同时，从各个不同的方向消除地形影响(Yi et al., 2001)，对电磁勘探数据处理解释的多样性是有意义的.本文通过对地形影响基本规律及经典比值校正原理的分析，用实测标准电阻率替代数值模拟中均匀半空间电阻率，利用地形影响随频率降低(或早到晚期)逐渐减弱的特征，以频点间或时间道间变化速率作为校正系数(闫述， 2015)，实现了依赖实测数据进行地形校正的方法.新的比值校正方法增加的工作量很小，为山地探测野外实时数据处理解释提供了快速简便的手段.仿真CSAMT和实测TEM校正实例表明，新的比值校正公式是有效的.

2 地形影响分析

造成地形影响的有几何因素和物理因素，主要包括(Hördt and Scholl., 2004)：(1)接收装置高于水平地表；(2)山体作为导电体置换了空气，或空气作为绝缘体置换了原属水平大地的一部分；(3)接收装置处于非水平状态，接收的不仅有磁(电)场的垂直(水平)分量，还有水平(垂直)分量的成分；(4)山体和地下构造的耦合.

2.1 地形影响的基本规律

对以电压值为基本观测量的电和电磁法勘探来说，实测电压或感应电动势与地形的变化反相，即地势高处降低，地势低处增高；地形对频域(CSAMT或MT)高频段数据影响较大，对时域(TEM)早期数据影响较大，随着频率降低或观测时间进入晚期，地形影响逐渐减弱.还有，地形变化剧烈处场变化剧烈，地形变化较平缓处场变化平缓；高阻表层地形影响小，低阻表层影响大.这种现象可由电流线在地形作用下的聚集和发散机理解释：在导电的大地中，随地势的起伏，山峰处电流线发散(密度小)，山谷处电流线聚集(密度大).电场强度与电流密度成正比(如图1所示)：

J=σE,

(1)

电压与电场强度成正比：

V=∫lE·dl.

(2)

因此实测电压值幅度的变化与地形的高低变化反相.

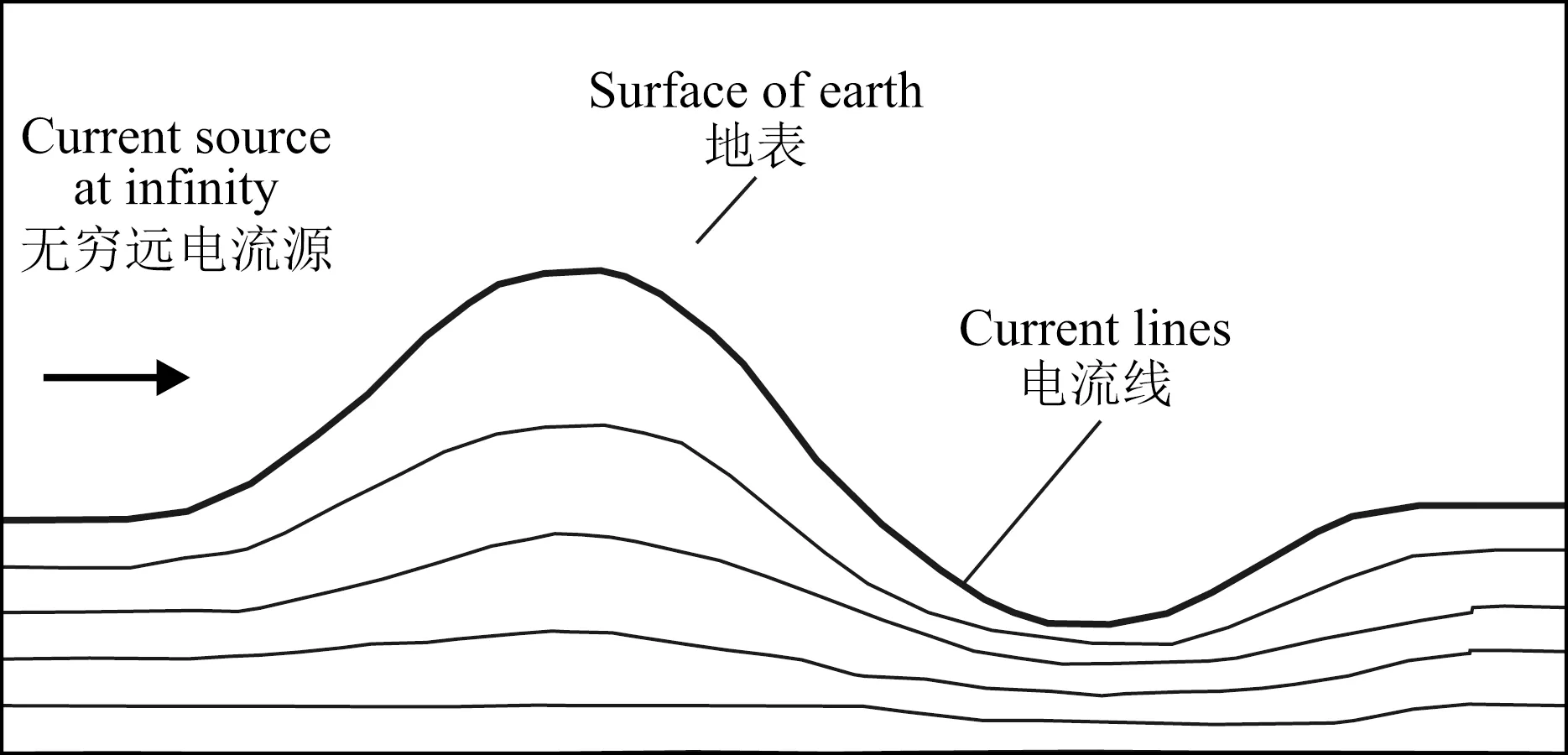
图1 地形对电流的聚集与发散作用Fig.1 The gathering and diverging effect of topography to current

地形影响的电流聚散机理无论对直流电法还是时域、频域的电磁法勘探都是相同的.时域的早期，相当于频域的高频或直流的小极距情况.但是，直流和频域中的视电阻率与电压(或电场)成正比，因此视电阻率变化与地形起伏仍然是反相的.时域瞬变场在低阻体中激发起较大的涡旋场，观测电压，也就是感应电动势EMF(Electromotive Force)随之增大；在高阻体中激发的涡旋场较小，EMF随之减小.这种特性在视电阻率上的反映就是其值与EMF值的大小变化相反，即视电阻率的变化与地形同相，地势高处视电阻率值增高，地势低处视电阻率值降低，表现出与频域和直流电法勘探不一样的特点.但这在本质上是相同的，都是地形对电流线的发散与汇集作用造成观测电压(电场)幅值的改变.地形影响的基本规律，是判断观测数据是否受到起伏地形影响、和影响程度的准则.

图2 边界元CSAMT电场地形影响模拟(a) 斜坡地形高程; (b) 斜坡地形视电阻率剖面.Fig.2 Boundary element modeling results of CSAMT(a) Slope model; (b) Apparent resistivity profile.

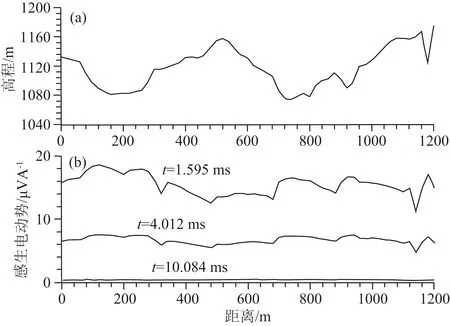
图3 陕西黄陵14线中心回线TEM实测地形影响(600 m×600 m)(a) 地形高程; (b) 实测EMF测道图.Fig.3 The topographic influence on central loop TEM data (600 m×600 m)(a) Topography; (b) Measured EMF curves.

2.2 地形起伏情况下数值模拟与实测数据

图2是二维纯地形CSAMT边界元模拟结果.其中图2a为地形，图2b是代表近、中、远区的3个频率沿线剖面图，源置于坐标原点.图3a是陕西黄陵煤矿中心回线TEM勘探L14线的地形剖面，图3b是代表早、中、晚期的实测EMF测道图.对照两图中地形起伏和电场或EMF沿线的变化，大致规律是：地形下凹处，EMF上凸；地形上凸处，EMF下凹；地形变化剧烈处EMF变化剧烈，随着频率的降低，或者从早期向晚期的时间过渡，地形影响逐渐减弱.因此，山地电磁法勘探中，接收点应尽量布置在地形较平缓处，减小地形异常对有用异常的干扰.但山势起伏总的影响仍然存在，校正是必要的.

3 比值校正方法

3.1 经典的比值校正公式

直流、频域或时域经典比值校正公式有相同的形式，均以视电阻率为校正参量(李金铭, 2005)：

(3)

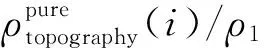
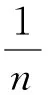
则实测值除以1/n(即乘以n)恢复正常值.

为避免比值校正时二、三维数值正演的巨大计算量，不因地形校正增加野外勘探工程的测地工作量，根据前述地形影响的基本规律，依据经典公式(3)的校正原理，给出新的比值校正公式利用实测数据本身达到校正的目的.

3.2 快速比值校正公式

新的频域CSAMT和时域TEM比值校正公式为

(4)

式中频点或时间道序数i从高频(早期)向低频(晚期)增加.公式(4)与经典比值校正公式(3)的不同之处为：

① 在各测点采用小极矩直流电法或通过岩土实验室测试，获得表层标准电阻率ρstandard，并用其替代公式(2)中均匀半空间电阻率ρ1.当表层较厚，如为巨厚黄土层，地表电阻率相差不大时，也可以用测区内的电测井资料作为各测点的标准电阻率.

小极矩观测的目的是避免地形影响，提供校正的标准.可先选适当极矩观测，当极矩缩小后测得的电阻率变化可忽略时，即认为地形影响可忽略.

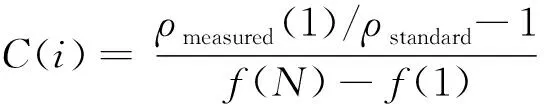
(5)

其中f(j)为频率，从高频到低频编号1～N.

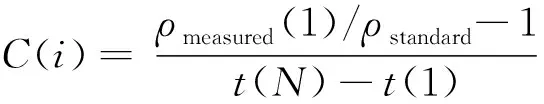
(6)

其中t(i)为时间道，从早期到晚期编号1～N.

为提高系数C(i)精度，可加密频点或时间道.需要说明的是，校正系数C(i)也可以是非线性的，这就需要通过钻孔、地质资料、地下挖掘等其他手段确定不同层位的标准电阻率，此时校正结果的精度更高.

3.3 快速地形校正适用范围

如果起伏地表下，目标地层平缓稳定，后续数据解释中可作为一维情况处理，那么新的、快速简便的地形校正是有意义的.如果探测深度范围内地质构造不能作为一维地层近似，采用带地形的三维反演就是必要的.巨大的计算工作量和测地工作量，是复杂地质构造勘探取得良好地质效果的必要代价.

快速校正法假设低频或晚期视电阻率已不受地形影响，并以此和标准电阻率一同作为校正的基准.若极端情况下，未能观测到不随地形变化的最低或最晚数据，或者低频端、特别是晚时间道信噪比不够，无法利用时，公式(4)的校正效果下降.如对探测有较高的精度要求，仍需采用公式(3)校正，数值模拟不可避免.

4 校正实例

4.1 CSAMT数据校正

图4a是较图2斜坡地形变化更为剧烈的正弦地形，图4b显示了典型的地形影响特征.对CSAMT仿真数据校正时，公式(3)中的ρstandard即为均匀半空间电阻率ρ1=100 Ωm.表1是所用的全部频率列表，校正后的结果示于图4.众所周知，CSAMT单分量远区视电阻率是大地真电阻率，是近区视电阻率的2倍，中区视电阻率随频率降低从远区过渡到近区(陈明生和闫述, 1995).将图4与图2较后可以看到，代表远区的f=7355 Hz视电阻率剖面为100 Ωm的直线，这是大地真实电阻率；代表中区的f=81.45 Hz视电阻率剖面成一斜线，代表近区的f=1.274 Hz视电阻率剖面为50 Ωm的直线.这表明，地形响应被消除，快速校正公式(4)对仿真的地形影响是有效的.

图4 仿真CSAMT地形影响校正(a) 地形剖面; (b) 校正前的CSAMT视电阻率剖面; (c) 校正后的CSAMT视电阻率剖面.Fig.4 Topographic influence correction for synthetic data of CSAMT(a) Topography profile; (b) Apparent resistivity curves before correction; (c) Apparent resistivity curves after correction.

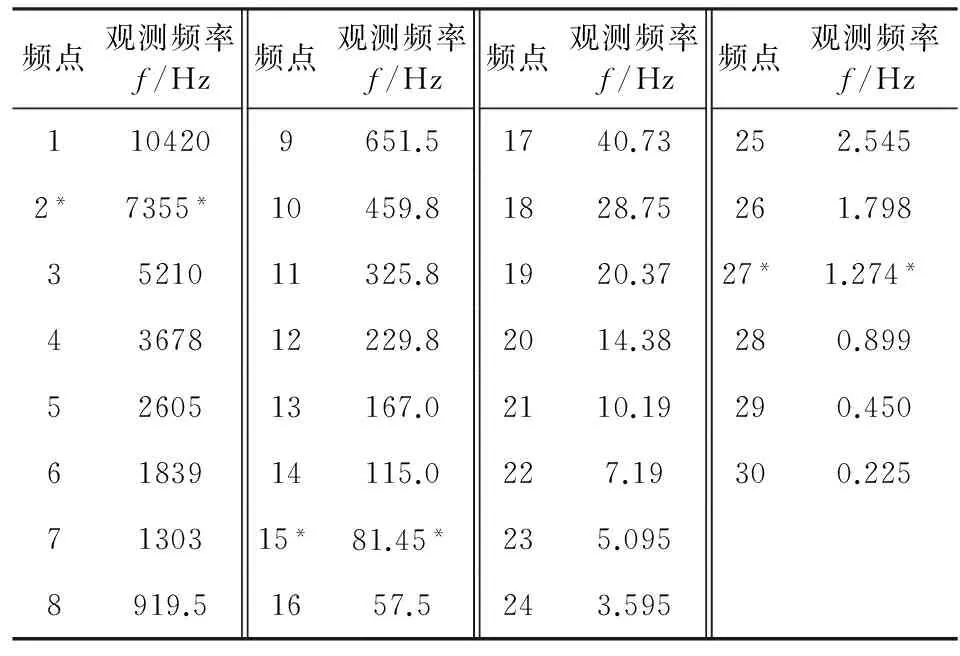
频点观测频率f/Hz频点观测频率f/Hz频点观测频率f/Hz频点观测频率f/Hz1104209651.51740.73252.5452*7355*10459.81828.75261.7983521011325.81920.3727*1.274*4367812229.82014.38280.8995260513167.02110.19290.4506183914115.0227.19300.2257130315*81.45*235.0958919.51657.5243.595

注：加*数字为实例采用的频点和频率.

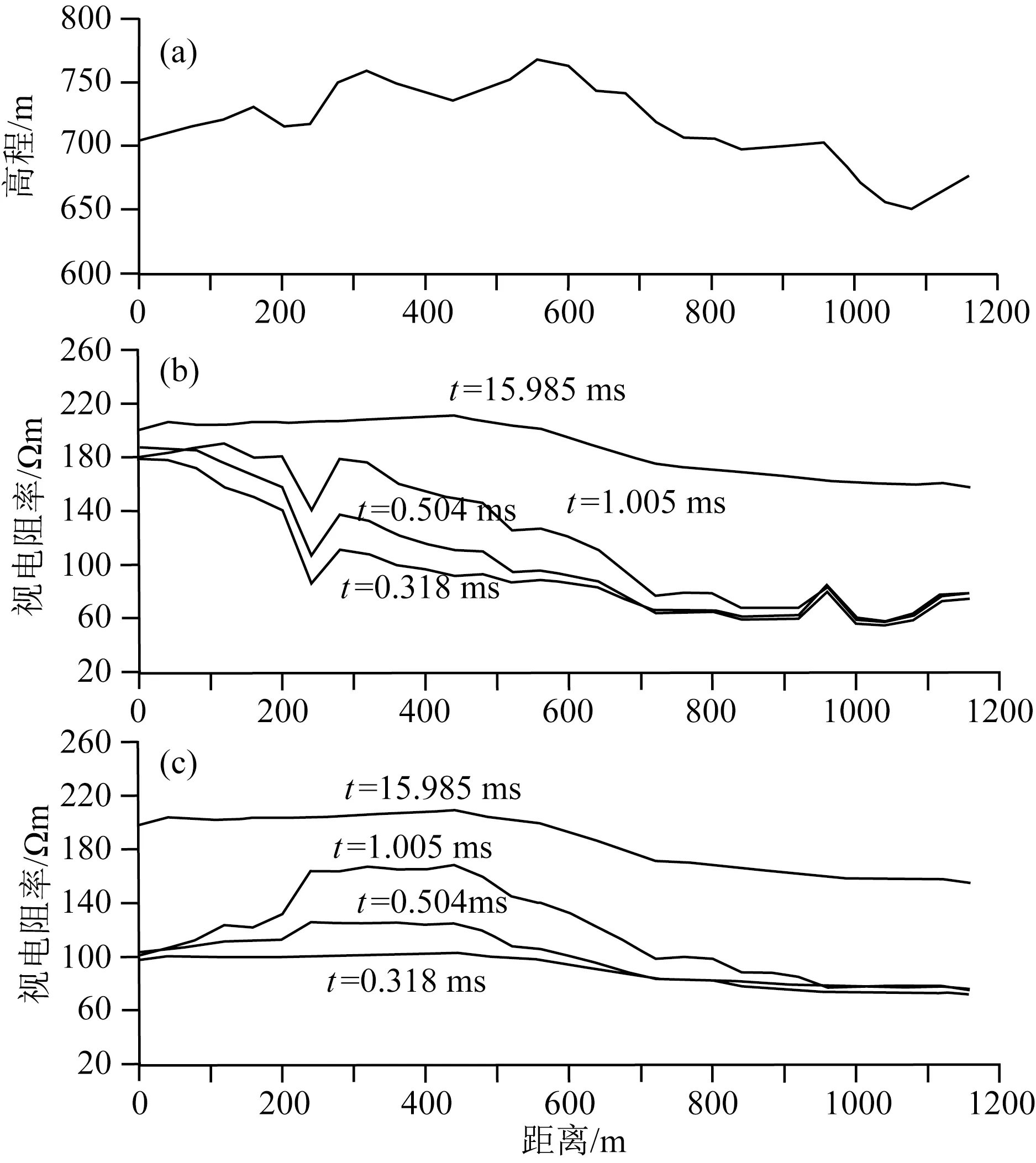
图5 实测TEM地形影响校正(a) 沿TEM测线的地形剖面； (b) 校正前的TEM视电阻率剖面； (c) 校正后的TEM视电阻率剖面.Fig.5 Topographic influence correction of field TEM data(a) Topography profile; (b) Apparent resistivity curves before correction; (c) Apparent resistivity curves after correction.

4.2 TEM实测数据校正

陕西黄陵煤矿地表为黄土冲蚀地形，下伏地层平缓、稳定，倾角在5°以内，符合快速地形校正的适用条件.所用中心回线TEM发射线框600 m×600 m、接收线圈等效面积100 m2，观测时长30 ms、20道.图 5a是沿线地形剖面，为表示清晰起见，图5b的实测TEM视电阻率剖面用了其中的t=0.318 ms、t=0.504 ms、t=1.005 ms、t=15.985 ms等4个时间道.表3列出了通过小极矩直流电阻率法获得的各测点地表电阻率值，作为公式(4)中的标准电阻率ρstandard.时域TEM视电阻率和地形(图5a)呈同相变化，即地形下降时视电阻率下降、地形上升时视电阻率上升，地形变化剧烈时(如图5b中的240 m、960 m处)视电阻率的变化也剧烈.根据地形的时域TEM响应特征，可以判断t=15.985 ms时刻地形影响消失，故取t(1)=0.318 ms、t(N)=15.985 ms，连同实测数据和表3作为标准电阻率的地表电阻率值代入公式(4)和(6)后，得到校正后的TEM视电阻率剖面(图5c).由图5可知，实测TEM视电阻率除了纯地形响应外，还耦合了地质结构本身的变化.但是地形影响校正仅去除地形影响，并保留地质结构响应，这种新的校正方法取得了较好的效果.

表2 实测TEM山地勘探时间道

注：加*数字为实例采用的时间道和观测时间.

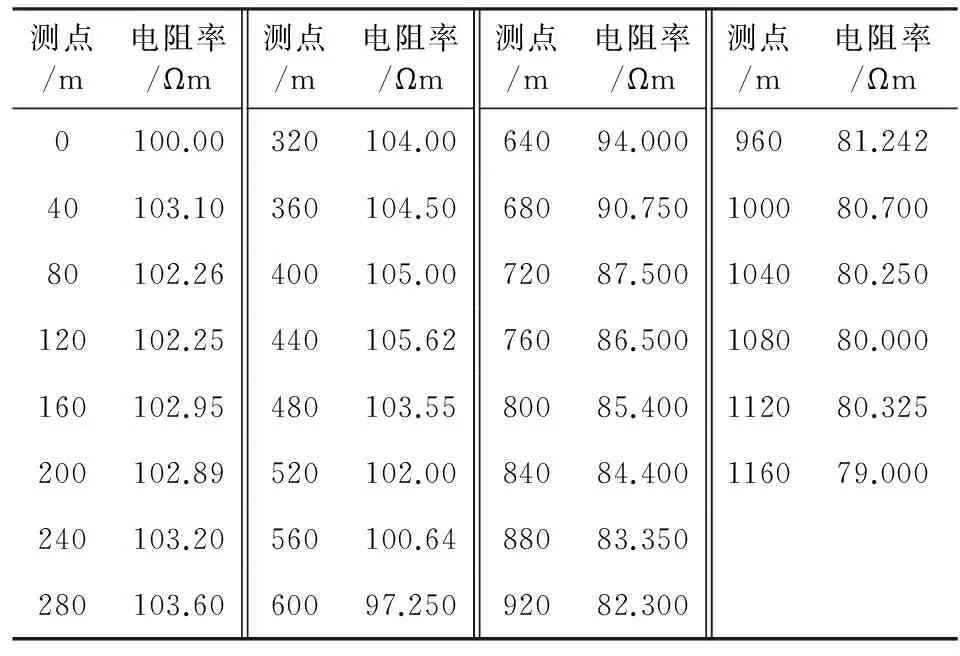
表3 小极矩直流电阻率法获得的各测点标准电阻率值

5 结论

本文通过对地形影响基本规律、经典比值校正原理的分析，用实测标准电阻率替代数值模拟中均匀半空间电阻率，利用地形影响随频率降低(或早到晚期)逐渐减弱的特征，以频点间或时间道间变化速率作为校正系数，针对地形对电磁法数据的影响提出了一种新的快速校正公式.本文提出的校正方法在实施过程中，除了测点以外，无须额外的地形高程测量，实现了依赖实测数据进行地形校正.同经典比值校正法一样，仅校正地形影响，保留了地质结构的响应.新的比值校正方法增加的工作量很小，为山地探测野外实时数据处理解释提供了快速简便的手段.仿真CSAMT和实测TEM校正实例表明，新的比值校正公式是有效的.

Chen M S, Yan S. 1995. Problems in Frequency Electromagnetic Soundings (in Chinese). Beijing: Geology Press.

Dong H, Wei W B, Ye G F, et al. 2014. Study of three-dimensional magnetotelluric inversion including surface topography based on finite-difference method.ChineseJ.Geophys. (in Chinese), 57(3): 939-952, doi: 10.6038/cjg20140323. Haber E, Oldenburg D W, Shekhtman R. 2007. Inversion of time domain three-dimensional electromagnetic data.GeophysicalJournalInternational, 171(2): 550-564.

Hördt A, Scholl C. 2004. The effect of local distortions on time-domain electromagnetic measurements.Geophysics, 69(1): 87-96.

Jiracek G R. 1990. Near-surface and topographic distortions in electromagnetic induction.SurveysinGeophysics, 1990, 11(2-3): 163-203.

Lei D. 2010. Studies and applications of 2-D CSAMT modeling and inversion with a dipole source and topography.ChineseJ.Geophys. (in Chinese),53(4): 982-993, doi: 10.3969/j.issn.0001-5733.2010.04.023.

Leppin M. 1992. Electromagnetic modeling of 3-D sources over 2-D inhomogeneities in the time domain.Geophysics, 57(8): 994-1003.

Li J M. 2005. Geo-electric Field and Electrical Exploration Methods (in Chinese). Beijing; : Geology Press.

Liu Y. 2012. Two-dimensional numerical modeling for topography Magnetotelluric/time-domain transient electromagnetic and direct inverse method [Ph.D. thesis] (in Chinese)., Chengdu: Chengdu University of Technology. Sun H F, Li X, Li S C, et al. 2013. Three-dimensional FDTD modeling of TEM excited by a loop source considering ramp time.ChineseJ.Geophys. (in Chinese), 56(3): 1049-1064, doi: 10.6038/cjg20130333.

Tang X G, Hu W B, Yan L J. 2011. Topographic effects on long offset transient electromagnetic response.AppliedGeophysics, 8(4): 277-284. Tong L T, Yang C H. 1990. Incorporation of topography into two-dimensional resistivity inversion.Geophysics, 55(3): 354-361. Wang X B, Li Y N, Gao Y C. 1999. Two dimensional topographic responses in magneto telluric sounding and its correction methods.ComputingTechniquesforGeophysicalandGeochemicalExploration(in Chinese), 21(4): 327-332. Wannamaker P E, Stodt J A, Rijo L. 1986. Two-dimensional topographic responses in magnetotellurics modeled using finite elements.Geophysics, 51(11): 2131-2144.

Wu X P. 2005. 3-D resistivity inversion under the condition of uneven terrain.ChineseJ.Geophys. (in Chinese), 48(4): 932-936. Xiao H Y. 2006. Three-dimensional numerical modeling considering the topography of TEM [Master thesis] (in Chinese). Beijing: China Universiity of Geosciences (Beijing).

Xu S Z, Zhou H. 1997. Modelling the 2D terrain effect on MT by the boundary-element method.GeophysicalPprospecting, 45(6): 931-943.

Yan S. 2015. One ratio method for correcting the topographic effect in electromagnetric exploration (in Chinese). Chinese Patent, ZL201310039614.6.

Yan S, Chen M S, Li Z M. 1996. Boundary element for method forward solution of two dimensional topography effection electromagnetic frequency sounding.ComputingTechniquesforGeophysicalandGepochemicalExploration(in Chinese), 22(4): 4533-4842, 47.

Yang D K, Oldenburg D W. 2012. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit.Geophysics, 77(2): B23-B34.

Yi M J, Kim J H, Song Y, et al. 2001. Three-dimensional imaging of subsurface structures using resistivity data.GeophysicalProspecting, 49(4): 483-497.

附中文参考文献

陈明生, 闫述. 1995. 论频率测深应用中的几个问题. 北京: 地质出版社, 1995.

董浩, 魏文博, 叶高峰等. 2014. 基于有限差分正演的带地形三维大地电磁反演方法. 地球物理学报, 57(3): 939-952, doi: 10.6038/cjg20140323.

雷达. 2010. 起伏地形下CSAMT二维正反演研究与应用. 地球物理学报, 53(4): 982-993, doi: 10.3969/j.issn.0001-5733.2010.04.023.

李金铭. 2005. 地电场与电法勘探. 北京: 地质出版社.

刘云. 2012. 起伏地形大地电磁、时间域瞬变电磁二维数值模拟及直接反演法[博士论文]. 成都: 成都理工大学.

孙怀凤, 李貅, 李术才等. 2013. 考虑关断时间的回线源激发TEM三维时域有限差分正演. 地球物理学报, 56(3): 1049-1064, doi: 10.6038/cjg20130333.

王绪本, 李永年, 高永才. 1999. 大地电磁测深二维地形影响及其校正方法研究. 物探化探计算技术, 21(4).: 327-332.

吴小平. 2005. 非平坦地形条件下电阻率三维反演. 地球物理学报, 48(4): 932-936.

肖怀宇. 2006. 带地形的瞬变电磁法三维数值模拟[硕士论文]. 北京: 中国地质大学(北京).

闫述. 2015. 一种校正电磁勘探中地形影响的比值方法. ZL201310039614.6.

闫述, 陈明生, 李志民. 1996. 频率测深二维地形影响的边界元素法正演模拟. 物探化探计算技术, 22(4): 4533-4842, 47.

(本文编辑 汪海英)

A fast topographic correction method for electromagnetic data

XUE Guo-Qiang1, YAN Shu2, CHEN Wei-Ying1

1KeyLaboratoryofMineralResources,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China2SchoolofComputerScienceandTelecommunicationEngineering,JiangsuUniversity,JiangsuZhenjiang212013,China

Topography generally affects the electromagnetic data and will mislead the results of shallow layer′s resistivity. In this paper, by analyzing the basic law of topography effect and classic ratio correction principle, it is feasible to replace the resistivity of uniform half space from numerical simulation by standard measured resistivity. We proposed a new fast method to correct the topographic effect in electromagnetic data. We obtain the surface resistivity without topography by using a small DC configuration, and then take it as standard resistivity to construct a new correction formula. Both synthetic and field data of CSAMT and TEM were processed using this method. Results show that the new method is a fast, effective and practical tool for topographic correction of electromagnetic data.

Electromagnetic method； Topographic effect； Correction； CSAMT； TEM

10.6038/cjg20161202.Xue G Q, Yan S, Chen W Y. 2016. A fast topographic correction method for electromagnetic data.ChineseJ.Geophys. (in Chinese),59(12):4408-4413,doi:10.6038/cjg20161202.

国家自然科学基金(41474095)，中国科学院矿产资源研究重点实验室开放课题，国土资源部煤炭资源勘查与综合利用重点实验室开放课题资助.

薛国强，男，1966年生，研究员，主要从事瞬变电磁法理论与应用研究. E-mail: ppxueguoqiang@163.com

10.6038/cjg20161202

P631

2016-02-04，2016-10-09收修定稿

薛国强， 闫述， 陈卫营. 2016. 电磁测深数据地形影响的快速校正. 地球物理学报，59(12):4408-4413,