非线性机电换能器混沌系统的分数阶控制及其电路仿真
2016-12-07王献锋王震张善文惠小健
王献锋, 王震, 张善文, 惠小健
(西京学院 应用理学系, 陕西 西安 710123)

非线性机电换能器混沌系统的分数阶控制及其电路仿真
王献锋, 王震, 张善文, 惠小健
(西京学院 应用理学系, 陕西 西安 710123)
通过数值分析计算一类自激机电换能器耦合系统的分叉、最大Lyapunov指数等混沌特性,并运用分数阶稳定性理论及Gershgorin圆定理证明并构造两个反馈控制器.采用所提方法,运用Multisim软件对机电控制系统进行电路实验仿真验证.实验结果表明:所设计的分数阶控制器对机电换能器的混沌控制是有效的,同时,电路设计具有可行性和可实现性.
机电换能器; 分数阶控制器; Vanderpol-Duffing振子; 混沌控制; 电路仿真
在电力系统等工程实际应用中,存在大量耦合Vanderpol-Duffing振子,其表现出来的混沌复杂性问题已成为研究的热点.为了研究耦合振子的动力学及分叉行为,奇异性理论、平均法、谐波平衡法等方法[1-2]被提出并利用.文献[3-4]考虑具有自动频率跟踪功能的电磁振动给料机的机电耦合系统的余维2动态分叉.张永祥等[5]研究振动筛系统余维3分岔行为.随着人们对机电耦合混沌系统的深入研究,大量的复杂非线性现象及系统的内在混沌动力学行为被揭示,同时,基于不同策略的混沌控制与同步方法在实验和应用中得到广泛验证.王从庆等[6]对三连杆空间机械臂系统,给出了鲁棒Proportional-Derivtive(PD)补偿控制、延迟反馈控制和模态力最优控制策略.文献[4-8]就一类机电耦合Vanderpol-Duffing系统,分别给出自适应反步控制及无源化控制方案.文献[9-11]对耦合Vanderpol-Duffing振子分别提出广义同步、延迟反馈控制、双Hopf分叉控制等方法.Arena等[12]研究低于2阶的分数阶非自治Duffing混沌系统;Li等[13]研究阶数小于3阶的分数阶混沌振荡电路的同步理论.由于分数阶导数的物理意义和几何意义还不清楚,尤其是在非线性系统理论中,分数阶混沌系统理论还非常不成熟,所以,目前分数阶混沌系统理论主要以数值仿真实验为主.因此,本文运用分数阶系统稳定性判据[14]对一类耦合Vanderpol-Duffing振子机电系统,即
(1)
设计了两种分数阶微分反馈控制器,并通过电路仿真对控制策略进行了验证.
1 分叉动力学
选取ε2=0.009 87,ε1=2.466,ω2=1,c=0,p=3.518,q=0.808,系统发生逆向倍式分叉,如图1所示.相应的最大Lyapunov指数图,如图2所示.由图2可知:随着参数的减少,系统状态经过周期运动进入混沌运动.

图1 参数ω1的分叉图 图2 参数ω1的最大Lyapunov指数图Fig.1 Bifurcation diagram with ω1 Fig.2 Largest Lyapunov exponent diagram with ω1
2 分数阶控制
引理1[15]假设x=0是自治系统dαx/dtα=A(x)x的一个平衡点,如果A(x)的任意特征值λ满足|arg(λ)|>απ/2,则系统平衡点渐近稳定.

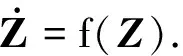
(2)
由文献[13]可知式(2)各局部动力学行为,为了对式(2)进行控制,取控制系统为
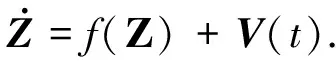
(3)
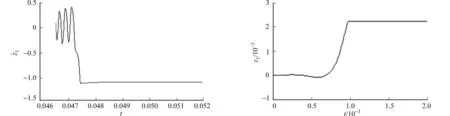
定理Ⅰ 当l1>1,l2>M2+pε2+ε1+1>0,l3>2,l4>1+M4-ε2>0,0 定理Ⅱ 当式(2)在常点Z0处的Jacobian矩阵不存在正实特征值时,可经过控制器稳定到常点. (4) 2) 如果Z0是式(2)的常点,则式(3)变为 (5) 且Z0为式(5)的平衡点,式(5)与(2)在Z0点处有相同的Jacobian矩阵,根据定理条件,则存在0<α0<1,且|arg(λ)|≥α0π/2,故0 图3 1/s0.9的单元电路Fig.3 Cell circuit of 1/s0.9 为了便于进行仿真实验,取与文献[14]相同的参数值,此时式(2)只含有一个零平衡点,即Z0=(0,0,0,0)T,取α=[0.9,0.9,0.9,0.9]T,分数阶1/s0.9的单元电路,如图3所示,其相应的电路方程为 图4 式(4)的电路原理图Fig.4 Circuit diagram of system (4) 图5 式(4)的稳定状态 图6 式(5)的稳定状态Fig.5 Stable state of system (4) Fig.6 Stable state of system (5) 运用分数阶微积分理论及Gershgorin圆定理,结合反馈控制法对一类Vanderpol-Duffing耦合机电系统设计了两个分数阶微分反馈控制器.同时,给出了严格的数学理论证明.运用模块化设计方法对控制策略进行电路设计与实验,证实了分数阶微分反馈控制器的可行性及可实现性. [1] LAMPART M,ZAPOMEL J.Dynamics of the electromechanical system with impact element[J].Journal of Sound and Vibration,2013,332(4):701-713. [2] YAMAPI R,FILATRELLA G,AZIZ-ALAOUI M A.Global stability analysis of birhythmicity in a self-sustained oscillator[J].Chaos,2010,20(1):013114. [3] 韩清凯,秦朝烨,闻邦椿.自同步振动系统的稳定性与分岔[J].振动与冲击,2007,26(1):31-34. [4] 张琪昌,田瑞兰.一类机电耦合非线性动力系统的余维2动态分岔[J].工程力学,2009,26(1):216-220. [5] 张永祥,孔贵芹,俞建宁.振动筛系统的两类余维3分岔与非常规混沌演化[J].物理学报,2008,57(10):6182-6187. [6] 王从庆,吴鹏飞,周鑫.基于最小关节力矩优化的自由浮动空间刚柔耦合机械臂混沌动力学建模与控制[J].物理学报,2012,61(23):230503. [7] WANG Zhen,WU Yuntian,LI Yongxin,et al.Adaptive backstepping control of a nonlinear electromechanical system with unknown parameters[C]∥Proceedings of the 4th International Conference on Computer Science and Education.Nanning:IEEE Press,2009:441-444. [8] 王震.非线性机电换能器混沌系统的无源化控制[J].控制理论与应用,2011,28(7):1036-1040. [9] KADJIA H G E,YAMAPI R.General synchronization dynamics of coupled Van der Pol-Duffing oscillators[J].Physica A,2006,370(2):316-328. [10] LI Xinye,CHEN Yushu,WU Zhiqiang,et al.Response of parametrically excited Duffing-van der Pol oscillator with delayed feedback[J].Applied Mathematics and Mechanics,2006,27(12):1585-1595. [11] MA Suqi,LU Qishao,FENG Zhaosheng.Double Hopf bifurcation for Vanderpol-Duffing oscillator with parametric delay feedback control[J].J Math Anal Appl,2008,338(2):993-1007. [12] ARENA P,CAPONETTO R,FORTUNA L,et al.Chaos in a fractional order duffing system[C]∥Proceedings of the European Conference on Circuit Theory and Design.Budapest:Technical University of Budapest,1997:1259-1262. [13] LI Chunguang,LIAO Xiaofeng,YU Juebang.Synchronization of fractional order chaotic systems[J].Physical Review E,2003,68(6):067203. [14] 王震,孙卫,惠小健,等.非线性机电换能器混沌系统的动力学分析与控制[J].制造业自动化,2014,36(10):25-30. [15] 张江源,林福泳.基于离散元的多分辨率信号去躁新方法[J].华侨大学学报(自然科学版),2013,34(3):130-133. [16] GERSCHGORIN S.Über die abgrenzung der eigenwerte einer matrix[J].Izv Akad Nauk USSR Otd Fiz: Mat Nauk,1931(6):749-754. (责任编辑: 黄晓楠 英文审校: 崔长彩) Fractional Order Control and Circuit Simulation for Nonlinear Electromechanical Transducer Chaotic System WANG Xianfeng, WANG Zhen, ZHANG Shanwen, XI Xiaojian (Department of Applied Science, Xijing University, Xi′an 710123, China) The chaos feature of the bifurcation and the largest Lyapunov exponent for a self-sustained electromechanical transducer coupled system are obtained by numerical analysis in this paper. According to the theories of fractional order calculus and the Gershgorin cycle theorem, two fractional order feedback controllers of this system are designed. The circuit implementation is simulated using Multisim for electromechanical control system by the proposed methods. And the simulation results demonstrate the effectiveness of the proposed fractional order controller for the chaos control of electromechanical transducer. Meanwhile, the circuit design is feasible and can be realized. electromechanical transducer; fractional order controller; Vanderpol-Duffing oscillator; chaos control; circuit simulations 10.11830/ISSN.1000-5013.201606020 2016-10-13 王献锋(1965-),男,副教授,主要从事非线性系统模型控制与优化的研究.E-mail:williamwangz@yeah.net. 国家自然科学基金资助项目(61473237); 陕西省自然科学基础研究计划项目(2016JM1024); 陕西省教育厅科研计划项目(15JK2181); 西京学院科研基金资助项目 (XJ130244) TP 273; TM 346 A 1000-5013(2016)06-0762-04
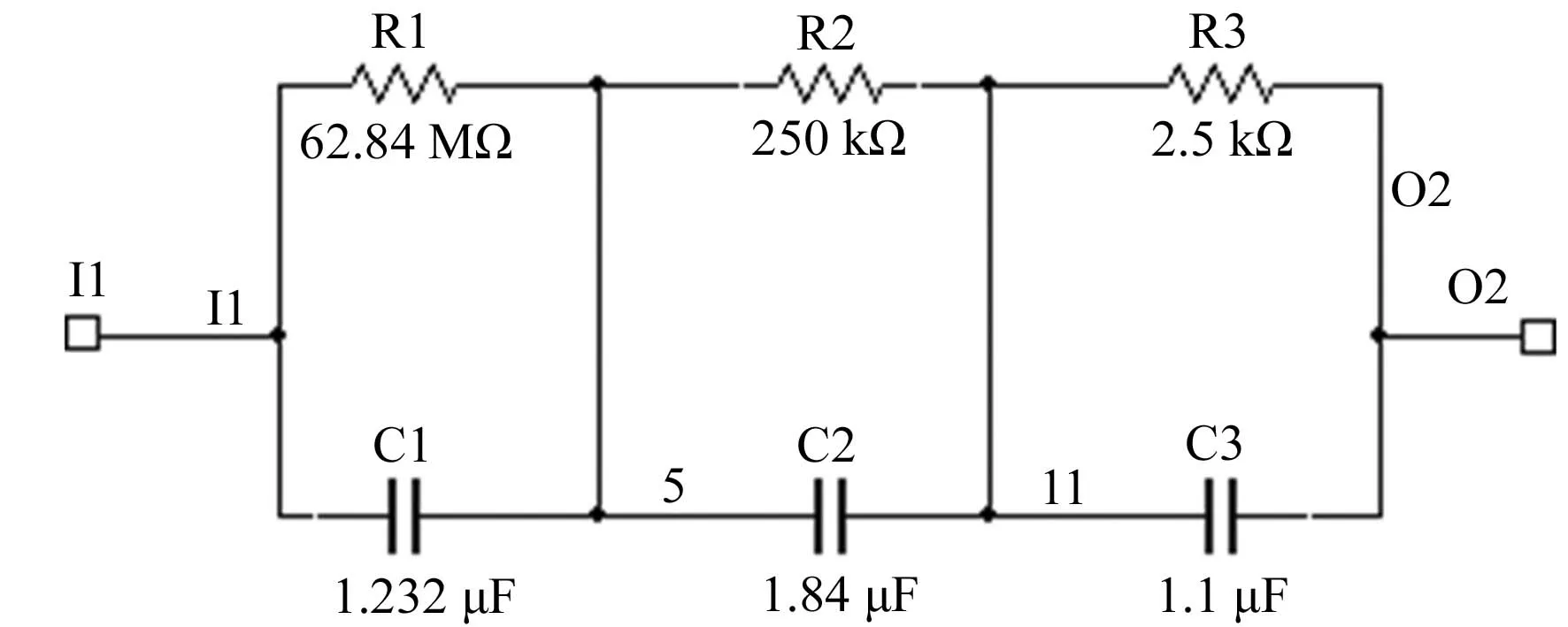
3 电路仿真
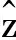

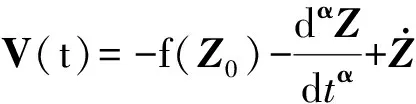
4 结束语
