全国10个地区城市建设情况的模糊聚类分析
2016-12-05高汉君
曹 丹,高汉君
(成都纺织高等专科学校建筑工程学院,四川成都 611731)
全国10个地区城市建设情况的模糊聚类分析
曹 丹,高汉君
(成都纺织高等专科学校建筑工程学院,四川成都 611731)
近几十年来我国土木工程建设飞速发展,全国各地区城市建设情况参差不齐,将全国10个具有代表性的地区城市建设情况的数据,通过Excel表格进行模糊聚类分析,将这些地区进行分类,找出建设发展进程相似的地区,为将来城市建设的进一步研究提供理论依据。
城市建设 模糊聚类 Excel 计算
0 引言
随着我国经济的飞速发展,全国各地区的城市建设也在加快脚步进行着,但毕竟每个省市的具体情况不同,因此发展的速度与进程都有相当大的差异。运用模糊聚类的方法,对全国31个省市自治区中的代表地区的数据进行处理,分析之后,再将其分类,便可以对全国各地的建设发展情况有一个更加深入的了解,对于今后的建设规划和经济投资都有一定的指导意义。
1 原始数据
1.1 数据来源
从中华人民共和国统计局的统计年鉴中,收集到了全国31个省市自治区2011年的建设情况。
1.2 数据说明
如表1所示,相关参数有:城区面积、建成区面积、城市建设用地面积、征用土地面积,以及城市人口密度。
该表格根据地域排序,由于数据过多,后面我们会用到Excel进行数据处理,因此我们抽取每个地域的前1-2个省市自治区,且由于该统计数据中,上海市缺失“城市用地面积”和“征用土地面积”两项指标,故去掉上海市。因此我们用来模糊聚类分析的对象最终确定为10个。

表1 全国10个地区城市建设情况 (2011年)
2 模糊聚类原理
设Z = { x1, x2, …, xn} 是n 个对象集合,每个对象的特征数据表示为
xi= ( xi1, xi2, …, xim) , i = 1 ,2 ,…, n ,利用标定方法,可以得到2 个对象xi和xj的模相似程序rij,于是就得到模糊相似矩阵
(1)
其中rij= 1 , rij= rji, j = 1 ,2 , …?, n.
定理[1]设R 是模糊相似矩阵,则存在一个最小自然数k ≤n ,使t ( R) = Rk ,并且对一切大于k 的自然数q ,均有Rq=Rk。
该定理说明了从一个Fuzzy 相似矩阵R 通过求R 的传递闭包,可构造一个Fuzzy 等价矩阵,并且运算有限次,即不超过n次.为了提高运算速度,可以用平方法R→R2→R4→…R2k→…,经过有限次运算后,一定有一个自然数(2k≤n),使R2k=R2k+1,于是t(R)=R2k。利用截关于对R2k进行等价分类,从而得到诸对象的评价结果[2]。
3 运用Excel和Matlab实现模糊聚类
3.1 计算均值和标准差
首先,在Excel中运用AVERAGE()和STDEV()[3],对各列数据计算其均值与标准差,结果如表2所示。

表2 全国10个地区建设情况均值与标准差
3.2 取得标准化数据矩阵
选取A13单元格,输入公式=(A1-A$11)/A$12,并在全数据区域内进行数据填充,得到表3,即用第1个至第10个地区的数据减去均值再除以标准差。

表3 标准化数据矩阵
3.3 求取模糊相似矩阵
(2)
3.3.1 计算
选取A23单元格,输入公式=SQRT((A$13-A13)^2+(B$13-B13)^2+(C$13-C13)^2+(D$13-D13)^2+(E$13-E13)^2),得到d12,同样,选取B23单元格,输入公式=SQRT((A$14-A13)^2+(B$14-B13)^2+(C$14-C13)^2+(D$14-D13)^2+(E$14-E13)^2),得到d12,以此类推,填充矩阵内的所有数据,将所有的d算出,得到表4。
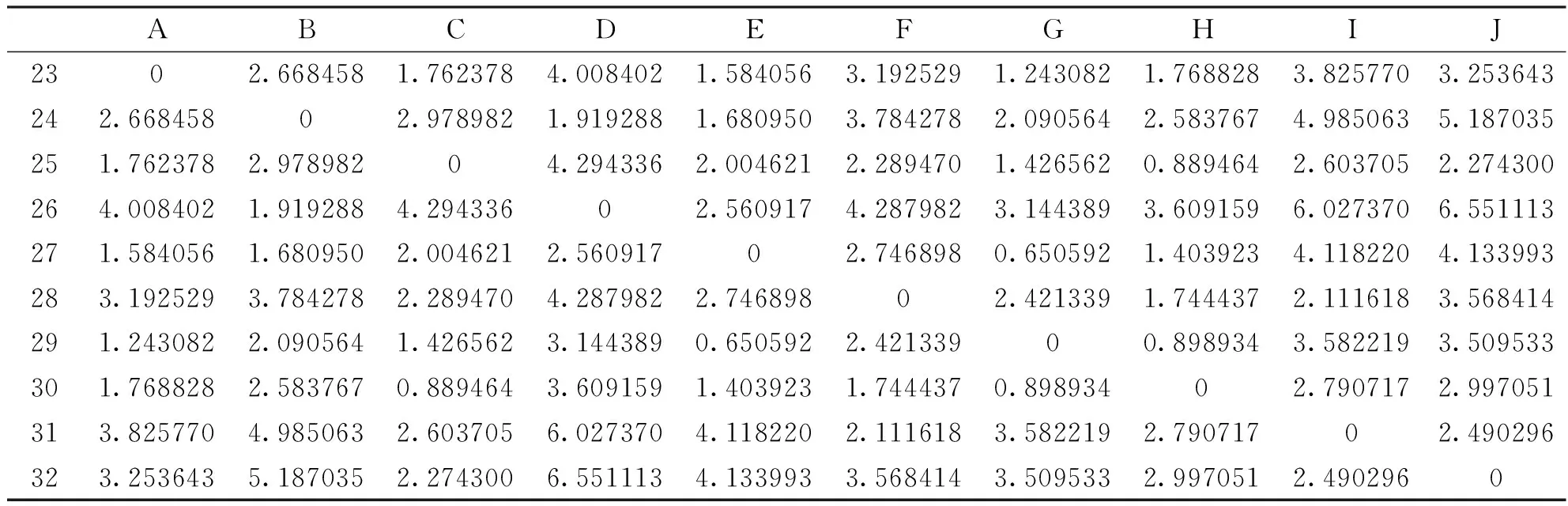
表4 d值
3.3.2 建立模糊相似矩阵
选取A33单元格,输入公式=1-A23/MAX($A$23:$J$32),求得 r11,然后在A33至J42区域中数据填充得到模糊相似矩阵R,如表5。

表5 模糊相似矩阵
3.4 求取模糊等价矩阵
在上述模糊相似矩阵的基础上进行模糊等价矩阵的求取。在单元格A43里输入公式=MAX(MIN($A33,A$33), MIN($B33,A$34),MIN($C33,A$35),MIN($D33,A$36), MIN($E33,A$37),MIN($F33,A$38),MIN($G33,A$39),MIN($H33,A$40), MIN($I33,A$41),MIN($J33,A$42)),然后相应地进行数据填充,得到R2,如表6,重复执行操作,即可得到R4、R8、R16……,直到出现Rk=R2k,则为模糊等价矩阵,即传递闭包,如表7。
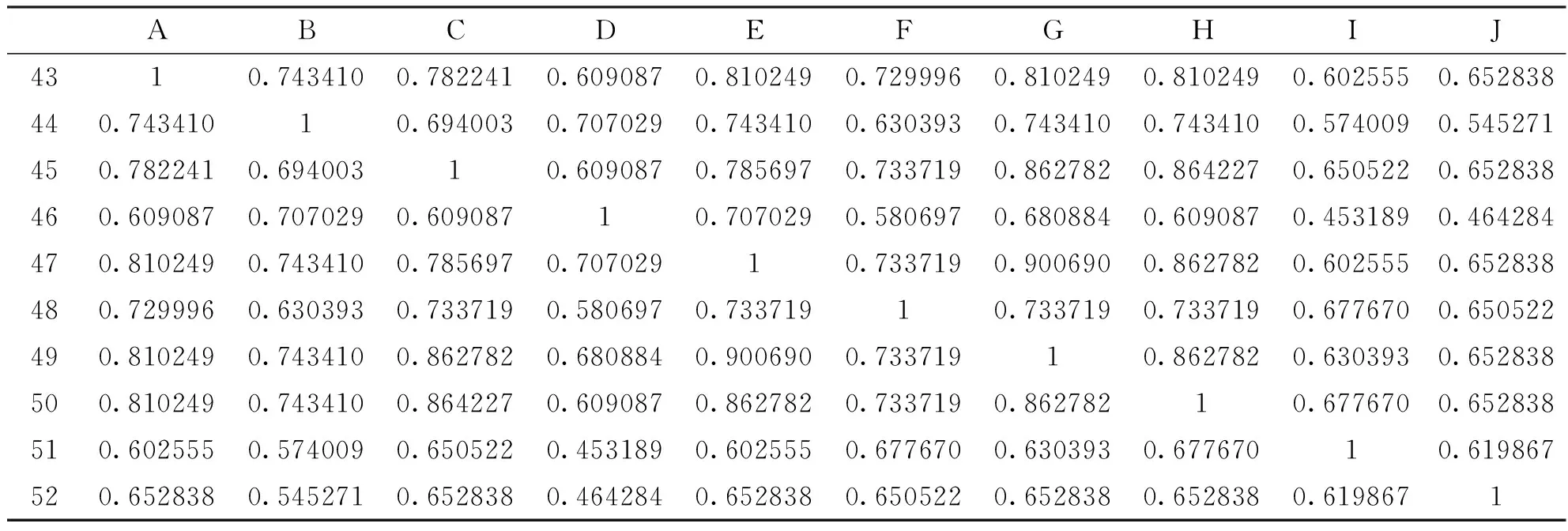
表6 R2
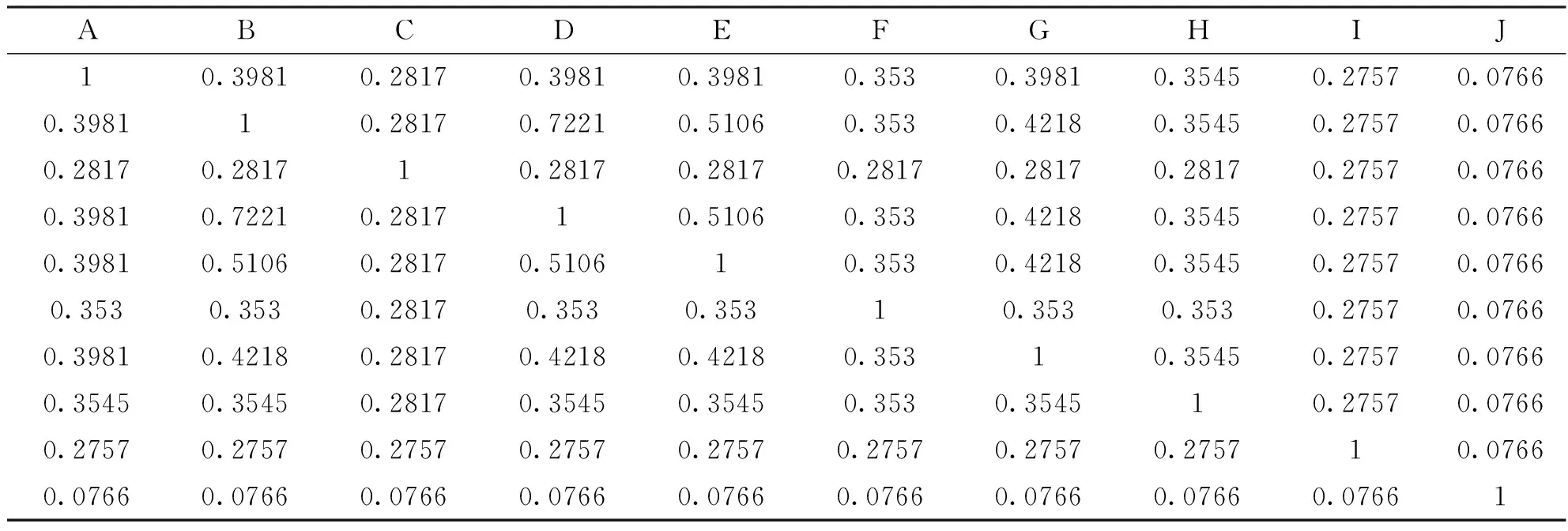
表7 模糊等价矩阵
(表7为MATLAB软件得出)
3.5 模糊聚类
由MATLAB进行模糊聚类,得到动态聚类图,如图1。

图1 动态聚类图
由图1可见,最先聚类的是2和4,故根据2和4最先聚类由大到小选择阈值λ,进行模糊聚类。新建一个表格,在A11单元格中输入=IF(A53>=λ,1,0),则得到模糊等价矩阵的截距阵。如λ=0.7,则2和4聚为一类,如表8

表8 模糊等价矩阵的截距阵(λ=0.7)
当λ=0.5时,则2、4、5聚为一类,如表9

表9 模糊等价矩阵的截距阵(λ=0.5)
当λ=0.4时,则2、4、5、7聚为一类,如表10

表10 模糊等价矩阵的截距阵(λ=0.4)
当λ=0.38时,则1、2、4、5、7聚为一类,如表11

表11 模糊等价矩阵的截距阵(λ=0.38)
当λ=0.354时,则1、2、4、5、7、8聚为一类,如表12

表12 模糊等价矩阵的截距阵(λ=0.354)
当λ=0.35时,则1、2、4、5、6、7、8聚为一类,如表13
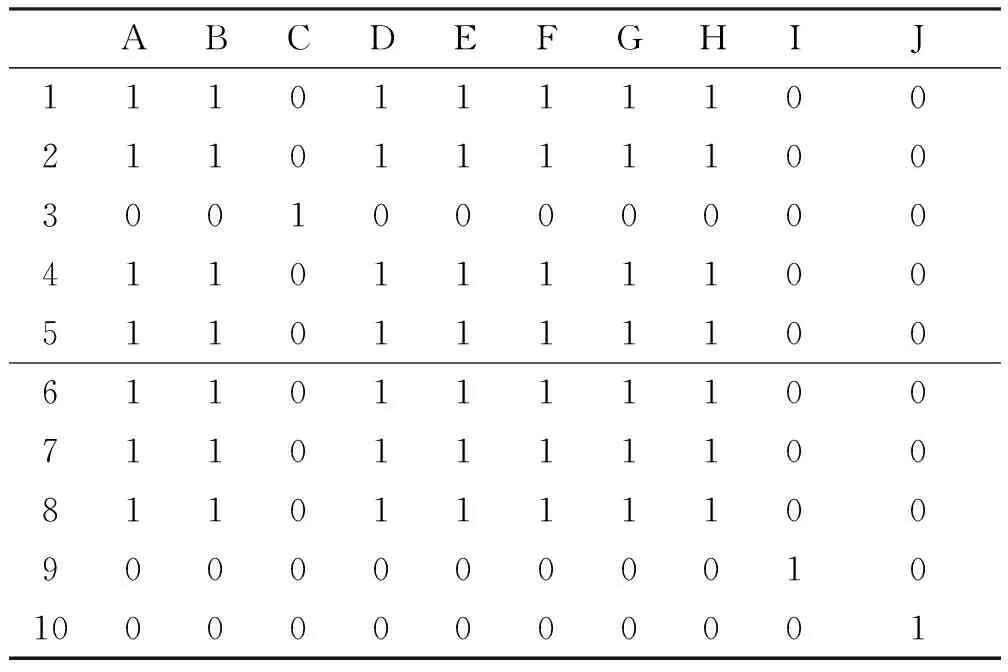
表13 模糊等价矩阵的截距阵(λ=0.35)
当λ=0.28时,则1、2、3、4、5、6、7、8聚为一类,如表14
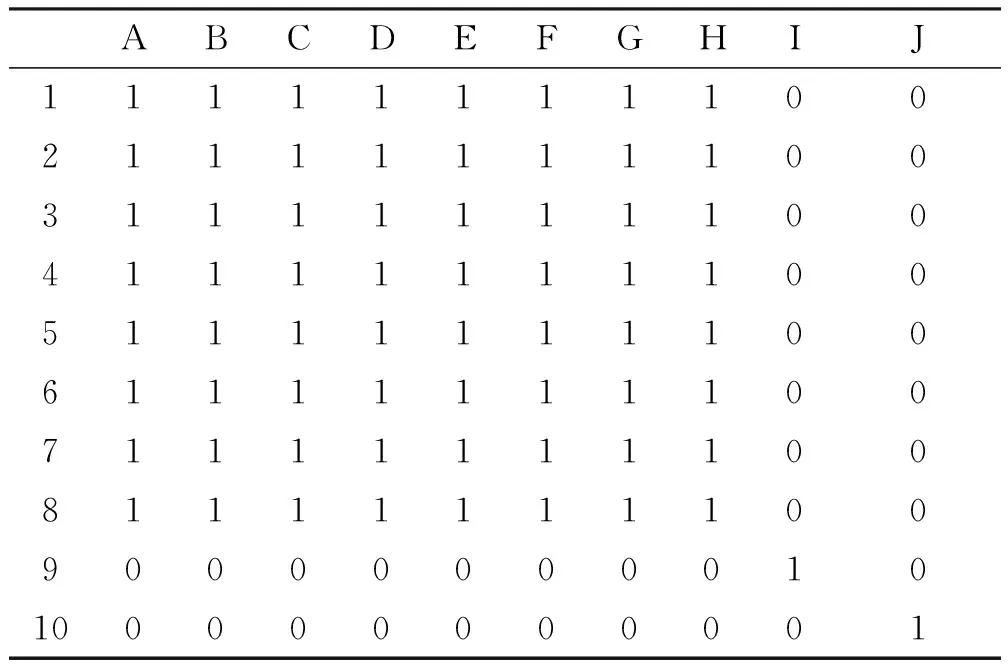
表14 模糊等价矩阵的截距阵(λ=0.28)
当λ=0.2时,则1、2、3、4、5、6、7、8、9聚为一类,如表15

表15 模糊等价矩阵的截距阵(λ=0.2)
当λ=0.05时,则全部聚为一类,如表16

表16 模糊等价矩阵的截距阵(λ=0.05)
4 模糊聚类分析及结论
由上面的各个模糊等价矩阵的截距阵得到以下结论:
以上聚类的各个地区,在不同λ值范围内分为同一类的地区,为城区面积,建成区面积等5个指标的情况相似的地区。
[1] 李洪兴,汪培庄. 模糊数学[M].北京:国防工业出版社,1993:86-291.
[2] 寇业富.大学生素质评价的模糊聚类分析[J].辽宁师范大学学报(自然科学版),2003(6):130-133
[3] 许永安,徐恒玉.用Excel实现模糊聚类分析[J].安徽农业科学,2005(1):740-742
2015-11-25
曹丹(1987-),女,硕士,助教,研究方向:管理科学与工程。
C931
A
1008-5580(2016)04-0242-05
