基于自适应流形去噪的视频运动分割算法

杨章琼

(宜宾职业技术学院， 四川 宜宾 644000)



基于自适应流形去噪的视频运动分割算法

杨章琼

(宜宾职业技术学院， 四川 宜宾 644000)

针对现有运动分割算法的不足，提出一种新的运动分割算法，通过自适应流形去噪实现刚性和非刚性对象的运动分割。首先，引入一种自适应核空间，如果2个特征轨迹属于同一刚性对象，则将其映射到相同点上。然后，采用一种基于自适应内核的嵌入式流形去噪算法分割出刚性和非刚性对象的运动，证明了对内核空间进行流形去噪等价于在列空间进行流形去噪。结果表明，该自适应流形去噪算法适合于刚性和非刚性运动分割，在多种当前最新算法均失效的场景下，算法仍然具有优异性能。

视频运动分割； 计算机视觉； 自适应流形去噪； 核空间

0 引 言

视频运动分割问题[1-2]是计算机视觉和图像理解领域的一个重要研究课题，其目的是通过一组图像或视频序列来预测并估计对象在一段时间内的运动。它也是许多实际应用中一个重要的计算机视觉处理步骤。传统的视频运动分割方法[3-5]将视频序列中的每一帧图像分离为相干二维或三维运动的不同区域(光流)。然后，研究人员将包含不同运动对象的场景综合起来，试图将每个对象及其运动作为一种相干实体进行识别。这些研究可以分为仿射算法和透视算法[6-9]。文献[7]中提出一种多特征稳健主成分分析(MFRPCA)算法，文献[8]中提出一种基于时空信息的运动对象分割算法。文献[9]中提出一种基于全局运动补偿和核密度检测的动态场景下视频运动对象分割算法。然而，之前的研究均假设同一对象的关键点位于严格的仿射子空间上，该假设在许多实际应用中尤其是出现非刚性对象时并不成立。更糟糕的是，类似对象在带噪流形上往往具有共同的区域或子空间，使传统算法难以用于对象分割。

本文提出一种新的运动分割算法。该算法假设对象点的轨迹位于平滑流形上，并通过自适应流形去噪获得分割结构。实验结果表明，本文算法对刚性和非刚性运动分割均具有优异性能。在部分场景下即使当前其他算法失效，本文算法仍然有效。

1 多人体视频运动分割

本文从多个仿射角度分析了三维运动分割问题的几何特征，并证明该问题等价于对高维空间的多个低维线性子空间进行聚类。这一问题可表述如下：假设运动点轨迹对应于相对摄像机进行C种不同刚性人体运动的C个对象，在该条件下，根据C个运动对轨迹进行聚类。此外，大多数真实应用场景既需处理刚性对象又需处理非刚性对象。例如，机器人需要从刚性环境中采集信息，又需识别人体等非刚性对象。先前算法[6-9]并不能同时处理刚性和非刚性对象。

1.1 刚性人体运动的运动子空间

摄像机变换往往为仿射变换，对于帧f中图像点Xp∈P3的非均匀坐标xfp∈R2，满足如下投影方程：

(1)

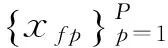
(2)

1.2 多对象刚性人体运动的运动子空间

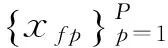
(3)

(4)

其中:S表示分块对角矩阵，有多种方法可实现上述分解[10-11]。本文重点研究假设通过热传播过程由平滑低维流形生成B后的直接聚类算法，即B图像的子空间可被认为是R2F中Grassmannian空间上的点。

2 自适应流形去噪

自适应流形去噪的目的是删除传感器、关键点匹配和非刚性效应带来的噪声。然而，先前的流形去噪算法[12]无法直接应用于运动分割问题，本文提出一种新的基于流形去噪的运动分割算法。

2.1 流形去噪

文献[12]中的流形去噪模型假设数据点位于带有噪声的未知p维流形M上，其中维度p为数据中的独立参数数量。更具体地讲，假设数据从平滑流形M:i→Rd映射到特征空间Rd上，其中d表示数据的初始维度，且数据受到噪声干扰，形式如下：

(5)

(6)

(7)

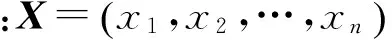
(8)

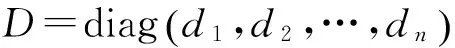
(9)

其中:σ表示模型参数。为了求解式(7)中的微分方程，本文采用隐式欧拉算法[13]，可得：

(10)

(11)

为了将核矩阵作为输入进行处理，求解如下问题：

(12)

其中:

φ表示从x到内积为〈·,·〉H的希尔伯特空间H的核映射，对元素x,y可以通过核函数

进行评估。

2.2 嵌入式流形去噪

(13)

下面证明基于式(12)和(13)进行更新从理论上来说可以获得等价结果。具体来说，有如下定理：

(14)

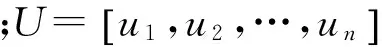
(15)

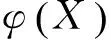
(16)

由于相同的原因，

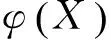
(17)

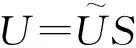
证毕

定理1表明，在其PCA子空间和在核空间进行流形去噪是等效的。本文中，已知核矩阵K后，进行特征值分解：

(18)

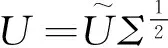
2.3 面向运动分割的自适应内核

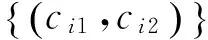
(19)

很显然，如果：

(20)

则：

(21)

这表明：

(22)

依据上述分析，对投影P，来自同一对象的点被投影到同一点上。然后，利用如下投影作为新映射：

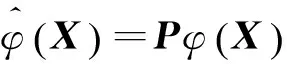
(23)

采用投影后，投影后的核函数可表示为：

(24)

证明

其中：

证毕

综上所述，局部增强内核的构建方法如下。

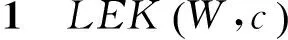
输入：特征轨迹数据X，约束集合c。

K=W

Sij=Kci1ci2-2Kci1cj2+Kcj1cj2,对c中的每个i,j

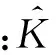
2.4 局部子空间内核

(2) 局部子空间估计。对每个点i，利用向量间的角度或其欧氏距离作为度量来计算点i第k个最近邻。然后，就局部子空间Bi对点及其近邻进行拟合。子空间Bi的维度di取决于运动类型(比如普通运动，完全平移运动，等等)及三维点的位置(比如普通位置，所有点均位于同一平面上，等等)，利用模型选择方法来确定维度di。

(3) 相似度图形构建和谱聚类。将成对点i,j=1,2,…,P间的相似度矩阵计算为：

(25)

然后对相似度矩阵W执行文献[9,7]中的谱聚类操作。

2.5 自适应流形去噪算法

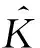
输入：轨迹数据X，聚类数量C。

步骤1：利用式(25)计算K=W。

步骤2：对W中的非对角线元素排序，选择最前列的αC对数据作为集合c。

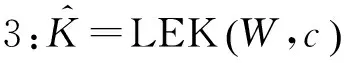
步骤4：

fort=1:Tdo

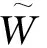
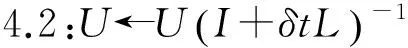
endfor

步骤5：通过谱聚类将数据点划分为U上的C个类别：π1,π2,…,πC。

3 仿真实验

3.1 实验设置

本文利用2个数据集评估本文算法。第一个数据集是文献[4]中的Hopkins 155数据集，它包括155个动作序列(120个二运动序列和35个三运动序列)。该数据集是运动分割标准数据集，包含刚性和非刚性运动对象，但是分辨率较低，且序列中存在错误匹配关键点。第2个数据集(在结果表中表示为Nonrigid(非刚性))包含3个视频运动序列，用于测试流形去噪算法的性能。这些视频序列的分辨率较高，且用手动方式删除被错误匹配的关键点。丢弃错误匹配的关键点的目的是将非刚性运动效应之外的所有扰动删除。我们采集视频的分辨率为(1 280 × 720)，并仔细选择轨迹关键点，以便主要扰动来自于非刚性运动而不是非匹配关键点或其他噪声。所以，这些序列适合于测试流形去噪的性能。为了验证本文算法的有效性，将本文算法与目前较为典型的广义主成分分析法(GPCA)、LSA算法(本文采用LSA的两种配置：5个最近邻算法和4C个最近邻算法)[14]、随机样本合意算法(RANSAC)[9]、投影因式分解(PF)算法[10]和多阶段学习算法(MSL)[15]进行了比较。

3.2 结果评估

用3种标准指标比较上述各算法的性能：聚类精度，正规化互信息(NMI)和纯度。结果见表1(Avg表示平均测量值，Med表示中位数)。从表1可以看到，对于精度、NMI和纯度等各个指标，本文算法的性能均优于其他各种算法，如表1黑体所示。对非刚性运动序列(交通和非刚性序列)，本文算法的性能远优于其他算法，对非刚性序列尤其如此。之所以实现性能提升，是因为采用了流形去噪过程。只要对象为平滑对象(从流形角度)，则流形去噪便能取得显著效果。LSA5和LSA4n的平均精度为74.25%和74.30%，低于本文算法(97.09%)。对非刚性类别，本文算法在其他两个指标上的性能几近完美，而其他算法的表现远低于本文算法。

AMD的总体聚类精度为98.42%。我们还在表2中单独总结了二运动和三运动的聚类精度(包括非刚性对象)。对二运动和三运动序列，本文算法的总体聚类精度分别为98.94%和97.92%。在各种情况下，本文算法的性能均优于当前其他最新运动分割算法。

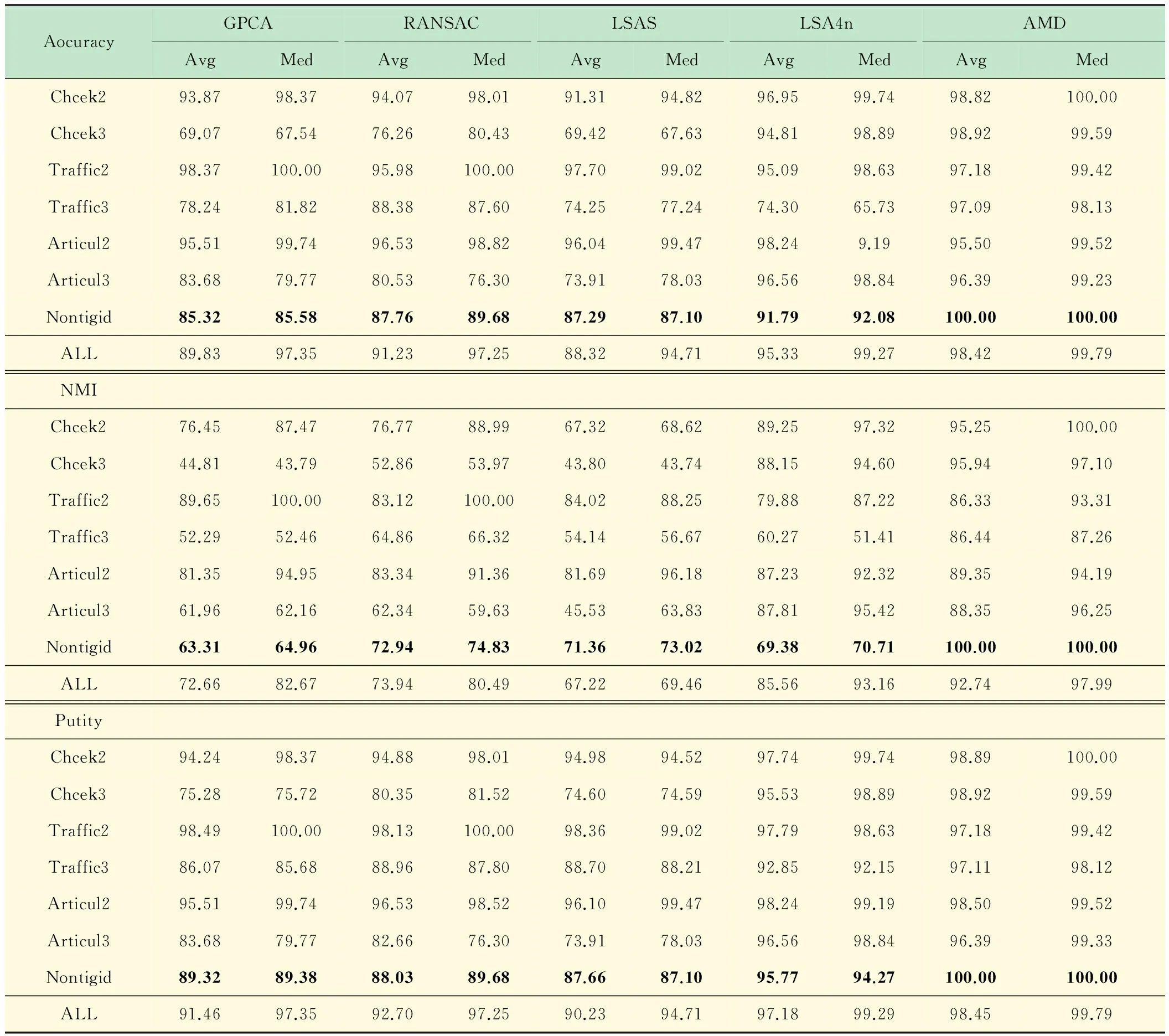
表1 几种方法的精度性能比较

表2 几种方法在整个数据集上的聚类精度性能比较

图1中给出了算法对非刚性运动分割的性能(交通数据集三运动和非刚性序列)。在该图中，如果一个点为a%累积百分比(x轴)和b%(y轴)精度/NMI/纯度，则表明至少有a%的数据点被正确分割的概率大于等于b%。可以看出，对这些非刚性序列，本文算法在各个指标上的性能均远优于其他算法。

GPCA, RANSAC, LSA5, LSA4n及本文算法对这3个序列的分割性能见图2。请注意，该图只给出了分组信息，即每张图片用同一标识(颜色)标记的关键点被相应算法划分为同一类别(对象)。可以发现，本文算法的分割性能远优于其他算法。

图2 GPCA, RANSAC, LSA5, LSA4n及本文算法(AMD)的关键点分割结果

4 结 语

本文提出一种新的视频运动分割算法，通过利用新的嵌入式流形去噪方法和局部增强核函数实现视频运动分割。由于存在噪声和离群点，在实际应用中进行运动分割的难度很大，导致传统的分割算法性能有限。通过研究轨迹所在流形的平滑度，本文算法可以获取刚性对象和非刚性对象等移动对象的隐藏结构。当其他多种最新算法失效尤其是同时存在刚性和非刚性对象时，本文算法仍然具有优异性能。

[1] 闵超波, 张俊举, 常本康, 等. 采用边界评价的红外视频运动目标时空域分割方法[J]. 红外与激光工程, 2013, 42(10): 2636-2641.

[2] 冯 林, 刘胜蓝, 王 静, 等. 人体运动分割算法: 序列局部弯曲的流形学习[J]. 计算机辅助设计与图形学学报, 2013, 25(4): 460-467.

[3] Ochs P, Malik J, Brox T. Segmentation of moving objects by long term video analysis [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(6): 1187-1200.

[4] Luo D, Huang H. Video Motion Segmentation Using New Adaptive Manifold Denoising Model[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR),Columbus, OH, USA: IEEE Press, 2014: 65-72.

[5] Galasso F, Keuper M, Brox T,etal. Spectral graph reduction for efficient image and streaming video segmentation[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA: IEEE Press, 2014: 49-56.

[6] Pan Y, Wang Y, Liu J,etal. Improved full analytical polygon-based method using Fourier analysis of the three-dimensional affine transformation [J]. Applied Optics, 2014, 53(7): 1354-1362.

[7] 甘 超, 王 莹, 王向阳. 多特征稳健主成分分析的视频运动目标分割[J]. 中国图象图形学报, 2013, 18(9): 1124-1132.

[8] 鲁梅, 卢 忱, 范九伦. 一种有效的基于时空信息的视频运动对象分割算法[J]. 计算机应用研究, 2013, 30(1): 303-306.

[9] 马志强, 张晓燕, 朱子健, 等. 一种动态场景下运动对象分割新算法[J]. 计算机工程与科学, 2012, 34(4): 43-46.

[10] Saha B, Pham D S, Phung D,etal. Clustering patient medical records via sparse subspace Representation[C] //Advances in Knowledge Discovery and Data Mining. Springer Berlin Heidelberg, 2013: 123-134.

[11] Hu H, Lin Z, Feng J,etal. Smooth representation clustering[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA: IEEE, 2014: 3834-3841.

[12] Wang B, Tu Z. Sparse subspace denoising for image manifolds[C]// 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA: IEEE Press, 2013: 468-475.

[13] Alfonsi A. Strong order one convergence of a drift implicit Euler scheme: Application to the CIR process [J]. Statistics & Probability Letters, 2013, 83(2): 602-607.

[14] Yan J, Pollefeys M. A general framework for motion segmentation: Independent, articulated, rigid, non-rigid, degenerate and non-degenerate[C]// 12thEuropean Conference on Computer Vision(ECCV), Firenze, Italy: IEEE Press, 2012: 94-106.

[15] Sugaya Y， Kanatani K. Geometric structure of degeneracy for multi-body motion segmentation[J]. In Statistical Methods in Video Processing, 2014, 11(23):13-25.

A Research on Video Motion Segmentation Algorithm Based on Adaptive Manifold Denoising

YANGZhang-qiong

(Yibin Vocational and Technical College, Yibin 644000, China)

Aiming at the disadvantages of the existing motion segmentation algorithms, a novel motion segmentation approach for both rigid and non-rigid objects is proposed by using adaptive manifold denoising. We first introduce an adaptive kernel space in which two feature trajectories are mapped into the same point if they belong to the same rigid object. After that, we employ an embedded manifold denoising approach with the adaptive kernel to segment the motion of rigid and non-rigid objects. We also show that performing manifold denoising on the kernel space is equivalent to denoising on its range space, which theoretically justifies the embedded manifold denoising on the adaptive kernel space. Experimental results indicate that our algorithm, named Adaptive Manifold Denoising (AMD), is suitable to both rigid and non-rigid motion segmentations. Our algorithm works well in many cases where several state-of-the-art algorithms fail.

video motion segmentation; computer vision; adaptive manifold denoising; kernel space

2015-12-12

杨章琼(1979-)，女，四川宜宾人，硕士，讲师，主要研究方向：图像处理、多媒体技术。

E-mail: 279J135162@qq.com

TP 391

A

1006-7167(2016)09-0041-06