柔性关节空间机械臂奇异摄动自抗扰控制仿真研究①

刘福才 李 倩 刘 林

(燕山大学工业计算机控制工程河北省重点实验室 秦皇岛 066004)



柔性关节空间机械臂奇异摄动自抗扰控制仿真研究①

刘福才②李 倩 刘 林

(燕山大学工业计算机控制工程河北省重点实验室 秦皇岛 066004)

针对不同重力环境条件下考虑摩擦、关节刚度非线性与外扰影响的柔性关节空间机械臂的控制问题，提出了一种基于奇异摄动理论的自抗扰控制方法。首先建立了柔性关节空间机械臂在地面重力和空间微重力环境下的动力学模型；然后采用奇异摄动法将系统模型分为快变子系统和慢变子系统，针对快变子系统设计速度反馈控制律来抑制柔性关节的振动，针对慢变子系统设计加入前馈补偿的自抗扰控制器(ADRC)来抵抗系统的内外扰动，并对系统进行了稳定性分析；最后对设计的控制器进行了仿真验证与对比研究。仿真结果表明，采用该方法，在不同重力环境下柔性关节空间机械臂均能实现很好的轨迹跟踪和抖振抑制，且能有效抵抗内外扰动，系统具有鲁棒性。

空间机械臂， 柔性关节， 重力， 奇异摄动， 自抗扰控制

0 引 言

随着空间站技术的迅速发展，在轨服务、深空探测等领域存在大量的空间任务需要完成，采用空间机械臂进行空间协助作业可以大大减轻航天员的出舱风险和工作压力，提高空间探索的效率，因此继加拿大、日本、欧洲、美国之后，世界各国纷纷开始空间机械臂的研制工作[1]。由于谐波减速器、行星齿轮等作为关节驱动部件具有减速比大、结构紧凑、传动效率高的优点，因此在空间机械臂中应用广泛。但随着速度和载荷的增大，这些驱动部件会导致关节柔性，带来滞后、非线性耦合和高频谐振等控制难题[2]。针对这一问题，本文对考虑了关节柔性的空间机械臂的控制进行了研究，提出了一种基于奇异撬动理论的自抗扰控制方法，并对该方法进行了仿真验证。

1 相关研究

由于进行空间机构的研究必须进行地面实验且应考虑空间应用时的微重力效应问题[3]，因此研究者们提出了多种微重力环境模拟方案。主要包括落塔/井法、失重飞机剖物线飞行法[4]、中性浮力法[5]、气浮法[6]以及吊丝配重法[7]。落塔与抛物线飞行可以实现高精度的微重力环境模拟，但模拟时间短、空间小，耗资高，对机构研究的实用范围有限。气浮法实验时间不受限，设备成本低且易于实现和维护，但只能实现平面模拟。中性浮力法和吊丝配重法可以进行三维模拟实验，但由于绳索柔性、设备中摩擦等阻力、大质量机构的运动惯量等因素，致使模拟的真实性较差。

目前，国内外学者针对柔性关节机械臂的控制问题做了大量的仿真研究。谢立敏等[8]针对参数不确定的漂浮基柔性关节空间机械臂的轨迹跟踪与振动抑制问题，提出了基于奇异摄动方法的鲁棒控制策略。陈明金等[9]针对具有时滞的柔性关节机械臂设计了自适应算法对系统参数进行修正，进行了机械臂的位置/力的跟踪控制研究。张奇等[10]设计了一种基于无源性理论的柔性关节控制器。Chien等[11]针对含时变不确定性的柔性关节机器人，设计了无需计算回归矩阵的模型参考自适应控制器来处理系统模型的级联结构与时变不确定性。Kandroodi等[12]提出了采用变结构控制结合混沌同步反控制实现柔性关节机械臂系统的轨迹跟踪与振动抑制的方法。这些研究在柔性关节机械臂的轨迹跟踪与振动抑制方面均取得了很好的控制效果，但这些研究只考虑了机械臂在地面或者在空间的情况，未考虑在地面装调好的机械臂应用于时是否仍能达到控制目标。

对于应用于空间的机械臂来说，由于缺乏有效的环境模拟试验验证手段，地面试验时重力的影响无法完全消除，因此需要设计考虑重力影响的控制器，使机械臂在地面与空间均能实现控制目标。 奇异摄动法是柔性关节机械臂控制中常采用的方法，采用该方法可以很好地处理柔性关节带来的系统抖振问题。该方法不仅适用于刚性/柔性机器人系统，在航天工程、过程控制、制造业和电力系统等领域也被广泛应用[13]。采用该方法进行系统设计时，首先忽略快变量以降低系统阶数，然后通过引入边界层来提高近似程度，相对于只考虑系统低频部分的做法更加准确。但奇异摄动法只适用于关节柔性较小的情况[14]。

基于此，本文提出了考虑不同重力环境的奇异摄动自抗扰控制器设计，对柔性关节空间机械臂分别在地面重力环境与空间微重力环境下进行轨迹跟踪控制仿真研究。首先，建立了地面和空间不同重力环境下考虑摩擦、关节刚度非线性、建模误差及系统外扰的柔性关节空间机械臂模型；其次，采用奇异摄动理论将系统分为快慢变子系统。针对快变子系统设计速度反馈控制律抑制柔性关节的振动，针对慢变子系统设计考虑模型信息的线性自抗扰控制器(active disturbance rejection controller, ADRC)来实现不同重力环境下机械臂的轨迹跟踪，将模型的已知部分作为前馈信息加入控制律中，采用扩张状态观测器(extended state observer, ESO)将建模误差及系统外扰估计出来并在控制律中进行补偿。并对控制系统的稳定性进行分析。最后对本文所设计的控制器，用MATLAB进行了仿真验证，并与其他控制方法进行了对比研究。

2 系统模型建立

本文考虑如图1所示的二自由度柔性关节机械臂。首先采用欧拉—拉格朗日方程，基于动能和势能推导出二自由度刚性关节机械臂的动力学模型，如下式所示：

(1)

柔性关节部分采用Spong[15]提出的经典简化模型，将电机和关节之间视为具有常值系数的线性扭转弹簧(示意图如图2所示)。当电机转子转过角度θi时，由于扭转弹簧作用，刚性杆转过的角度为qi，电机转子与杆件之间产生的角度变形误差为Δi=θi-qi。如果在动力学分析与控制中忽略柔性关节的存在，势必会造成变形误差的累积影响系统控制性能。考虑柔性关节的机械臂系统，在刚性机械臂的动能中加入电机转子的动能(假设其动能只由其自身的旋转引起)，再考虑柔性关节的弹性势能即可。转子动能Te和弹性势能Ue分别为

(2)

(3)

式中，Jm∈R2×2为电机的正定惯量矩阵，K∈R2×2为柔性关节刚度矩阵，θ为电机转子的角度矢量。

将弹性项与刚体动力学方程组合，可以得到由直流电机直接驱动的柔性关节机械臂的动力学方程如下：

(4)

式中，τm∈R2为电机产生的驱动力矩。杆的动力学和执行机构动力学通过弹性力矩项K(θ-q)耦合。

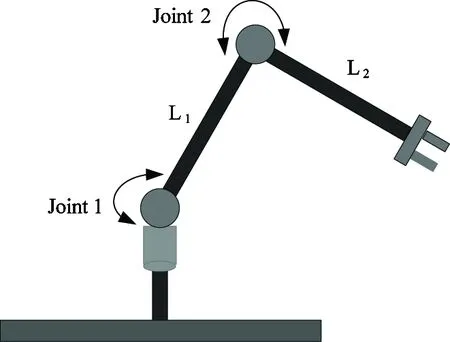
图1 柔性关节空间机械臂

图2 柔性关节简化模型

本文考虑关节刚度为非线性形式，非线性关节刚度动力学表达式为

(5)

式中，Ksw为对角正定阵，asw为用于定义柔性扭转函数的参数。

实际机械系统中存在摩擦力矩且不可忽略，因此需要考虑摩擦的影响并对其合理建模。本文选取摩擦力模型[16]如下：

(6)

式中，ri>0，i=1,2,…,6。

将上述摩擦模型加入到柔性关节空间机械臂模型中得到

(7)

式中，F∈R2为摩擦力矩矩阵。

地面装调阶段柔性关节空间机械臂的建模应该考虑重力，此时拉格朗日函数中增加了连杆的重力势能，得到地面阶段柔性关节空间机械臂的模型如下：

(8)

式中，G(q)∈Rn为重力载荷向量矩阵，可写成

G=φ(q)g

(9)

式中的g取0时，式(8)即为空间阶段柔性关节空间机械臂的模型。

由式(5)、(6)、(8)、(9)可以得到考虑不同重力、摩擦、关节刚度非线性、建模误差以及系统外扰的柔性关节空间机械臂模型

(10)

式中，Δ1∈R2为电机侧建模误差，Δ2∈R2为负载侧建模误差；wm∈R2为电机侧外界扰动项，wl∈R2为负载侧外界扰动项，重力载荷项G∈R2中的g在地面阶段取9.8，在空间阶段取0。式(10)中各矩阵表达式如下：

其中：

令，b=m2l1a2sinq2，则：

3 控制器设计与稳定性分析

3.1 控制器设计

关节柔性将导致系统的弹性振动，因此有必要设计能够同时实现轨迹跟踪与振动抑制的控制器。基于奇异摄动理论，将柔性关节空间机械臂系统转化为快慢变两个独立的子系统，然后分别针对两个子系统设计控制器[17]。

τm=τs+τf

(11)

式中τf是快变控制力矩，其作用是在突变情况下提供快速响应，用来消除系统的弹性振动。τm是慢变控制力矩，作用于准稳态系统，用来补偿系统的总和扰动，保证系统的轨迹跟踪。

由动力学模型式(10)，可以得到关节力矩τ(τ=K(θ-q))的方程

(12)

引入参数ε，取K=Kε/ε2，其中Kε为正定对角阵，ε越小表示关节刚度越大，并选取

(13)

则式(12)可重写为

(14)

令ε=0，得到关节力矩的准稳态表达式

(15)

将式(15)分别代入式(10)中得到考虑系统建模误差与外部扰动时的系统准稳态方程

(16)

针对准稳态系统设计二阶自抗扰控制器，以保证机械臂从地面到空间，系统模型发生变化时，以及系统在运行过程中参数发生变化，或者受到外界干扰时，均能实现很好的轨迹跟踪效果。

首先，为了简化控制器设计，将系统的准稳态方程写为如下的状态空间表达式：

(17)

式(17)与传统表达式的区别在于将b直接视为单位阵I2×2，u不是系统实际控制量τs，而是系统的虚拟控制量。

为了对扰动f进行估计，针对式(17)所示的系统设计三阶线性扩张状态观测器(ESO)形式如下：

(18)

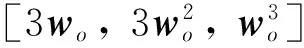
线性ADRC的控制律为如下线性组合形式：

u=u0-z3

(19)

式中，u0采用PD控制，其公式为

(20)

由式(17)、(19)、(20)可得到加入前馈控制量的慢变控制律为

(21)

在慢变控制律中加入前馈补偿，能有效减小ESO的观测带宽，避免放大测量噪声。系统的整体控制框图如图3所示。

图3 柔性关节空间机械臂奇异摄动自抗扰控制结构框图

3.2 稳定性分析

说明：文献[20]对线性ESO的估计能力进行了详细的证明，这里不再重复证明。

证明：由式(16)、式(21)可以得到系统的误差方程为

(22)

定义Lyapunov函数如下：

(23)

(24)

-αβλmin(Kp)‖e‖2

(25)

式中，λmax()和λmin()表示矩阵的最大特征值与最小特征值。又因为

(26)

(27)

(28)

所以

(29)

由此，定理得证。

4 仿真研究

采用本文设计的奇异摄动自抗扰控制律(见式(19))，对不同重力环境条件下考虑摩擦、关节刚度非线性以及系统外扰的二自由度柔性关节空间机械臂进行控制，首先对其轨迹跟踪情况、抖振抑制能力在MATLAB中进行了仿真验证。

(30)

由于关节柔性会引起系统抖振，因此需要对所设计控制器的振动抑制能力进行检验。正方形轨迹相对于圆形或者直线型轨迹，对控制器的要求更加严格，因此仿真时给定机械臂的期望轨迹为边长为12.6m的正方形。

机械臂的模型参数和摩擦模型参数分别如表1和表2所示。

表1 平面二连杆机械臂参数

表2 关节摩擦模型参数

电机的惯量矩阵为Jm=diag(1)，柔性关节的刚度非线性模型参数分别为a1=diag(500)，a2=diag(500)，Ksw=diag(500)。

控制器参数选择如下： Kp=[500 0;0 500],Kd=[50 0;0 50],Kv=[40 0;0 40],βo1=[150 0;0 80], βo2=[250 0;0 200], βo3=[1500 0;0 1000]。仿真结果如图4、图5所示。

从图4(a)与图5(a)可以看出，采用奇异摄动自抗扰控制在地面重力环境下和空间微重力环境下均可以实现很好的末端轨迹跟踪，只在轨迹跟踪的转角处出现微小的跟踪误差，但很快便可以恢复跟踪。从图4(b)与图5(b)可以看出，关节驱动力矩在方形轨迹的拐角处出现较大峰值，但抖振现象并不明显，说明该控制器具有很好的抖振抑制能力。从图4(c)与图5(c)可以看出，在轨迹跟踪转角处最大有0.1m的跟踪误差，其他位置最大有5×10-3的跟踪误差。从图4(d)与图5(d)可以看出，在大约为5s处，扰动的估计值可以完全跟踪上实际扰动值，说明观测器可以很好的对建模误差进行估计。

机械臂在轨服役过程中电机侧、负载侧均会受到外界扰动的影响，所以需要进行系统抗扰性能的研究。令w(w=wm+wl)为一个幅值为-20的阶跃扰动，开始时间为20s。仿真结果如图6所示。

图4 地面阶段奇异摄动自抗扰控制仿真图

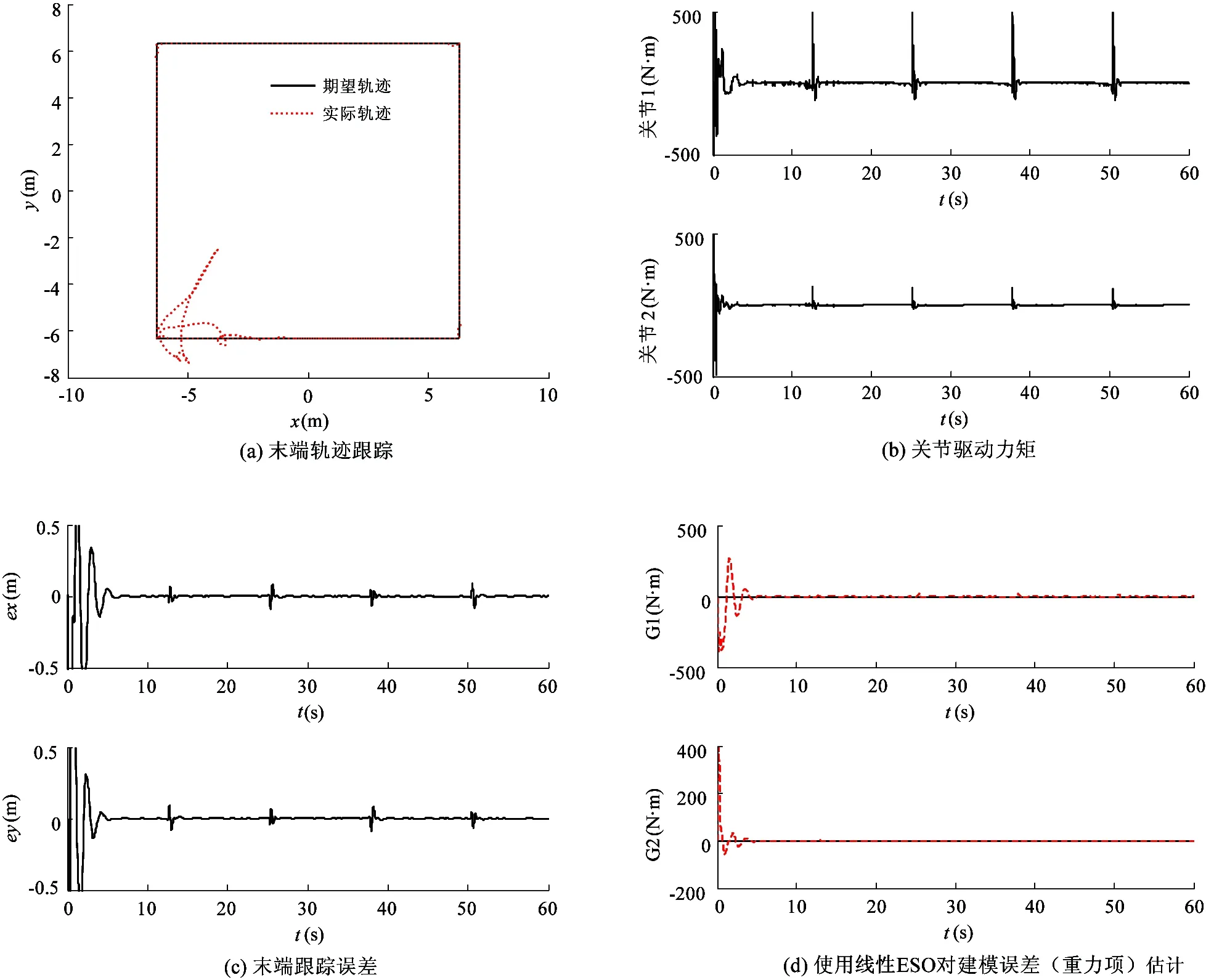
图5 空间阶段奇异摄动自抗扰控制仿真图

图6 空间阶段奇异摄动自抗扰控制抗扰性能仿真图

从图6(a)可以看出，在系统存在外界扰动时，空间柔性关节机械臂的末端轨迹仍能很好地跟踪期望轨迹，只在干扰进来时出现一个很小的跟踪偏差，之后便立即恢复跟踪。从图6(b)可以看出在20s时刻干扰进来时，线性ESO可以迅速将扰动估计出来，这也可以解释线性ADRC能够抗扰的原因。但是同样可以从图中看出，在方形轨迹的转折点处，扰动力矩的估计值都会有一个小的抖振，这是由于在轨迹转折点处要补偿的总和扰动突然发生变化。

5 控制性能比较

采用基于奇异摄动法的PD控制器(以下简称为奇异摄动PD控制器)对平面二连杆柔性关节空间机械臂进行了仿真研究(如图7和图8)，设计的控制律如下：

(31)

其中参数选择为Kp=diag(270), Kd=diag(150), Kvdiag(35)。

从图7可以看出，采用所设计的PD控制器，柔性关节空间机械臂在空间微重力环境下能基本实现轨迹跟踪，但是在地面重力环境下跟踪轨迹明显偏离了期望轨迹。说明PD控制器不能适应重力环境的变化，不具有鲁棒性。从图8可以看出，在地面与空间不同重力环境下，采用奇异摄动PD控制器对柔性关节空间机械臂进行控制时，驱动力矩在跟踪轨迹的转角处均存在严重的抖振。说明奇异摄动PD控制器的抑振能力较差。

图7 奇异摄动PD控制轨迹跟踪仿真图

图8 奇异摄动PD控制关节驱动力矩仿真图

另外，将本文的奇异摄动自抗扰控制与文献[2]的自适应鲁棒控制和文献[23]的神经网络控制进行对比，发现采用本文设计的控制器进行控制时系统的轨迹跟踪性能和抖振抑制效果更好。对扰动和建模误差的估计逼近更快、误差更小。

6 结 论

本文针对柔性关节空间机械臂在地面与空间阶段模型不同的问题，提出了基于奇异摄动法的自抗扰控制方法，并对该方法进行了仿真验证。仿真结果表明，采用该控制器对柔性关节空间机械臂进行控制时，在地面重力条件下和与空间微重力条件下均能实现较好的轨迹跟踪和抖振抑制，系统具有很好的鲁棒性。与自适应鲁棒和神经网络控制器相比，所设计的控制器实现简单，需调整参数少，工程上易于应用。

[1] 刘宏，蒋再男，刘业超． 空间机械臂技术发展综述． 载人航天，2015，21(5)：435-443

[2] 刘福才，高静方，李倩． 不同重力环境下的柔性关节空间机械臂自适应鲁棒控制． 高技术通讯，2015, 25(1)：61-69

[3] 刘春辉． 微重力科学与应用研究(上)． 宇航学报，1996, 4：110-114

[4] Hirokata Sawada，Kyoichi Ui，Makoto Mori，et al． Micro-gravity experiment of a space robotic arm using parabolic flight．AdvancedRoboticstheInternationalJournaloftheRoboticsSocietyofJapan，2004，18(3)：247-267

[5] Hirzinger G．Multisensory shared autonomy and tele-sensor programming — Key issues in space robotics．Robotics&AutonomousSystems，1993，11：141-162

[6] Ullman M A，Cannon R H，Rock S M． A modular system architecture for multi-manipulator，free-flying space robots． In：Proceedings of the 1993 IEEE International Symposium，Intelligent Control，Piscataway，USA，1993． 90-97

[7] Xu Y，Brown B，Friedman M，et al． Control system of self-mobile space manipulator．IEEETransactionsonControlSystemsTechnology，1994，2(3)：207-219

[8] 谢立敏，陈力． 漂浮基柔性关节空间机器人奇异摄动鲁棒控制． 振动、测试与诊断，2013，33(4)：597-601

[9] 陈明金，李树荣，曹乾磊． 时滞柔性关节机械臂自适应位置/力控制． 控制理论与应用，2015，32(2)：217-223

[10] 张奇，谢宗武，刘宏等． 基于无源性理论的柔性关节控制器设计． 机器人，2013，35(1)：23-31

[11] Chien M C，Huang A C． Adaptive control for flexible-Joint electrically driven robot with time-varying uncertainties．IEEETransactionsonIndustrialElectronics，2007，54(2)：1032-1038

[12] Kandroodi M R，Fariva F，Pedram M Z，et al． Variable structure control and anti-control of flexible joint manipulator with experimental validation．In：Proceedings of the 2011 IEEE International Conference on Mechatronics (ICM 2011)，Istanbul，Turkey，2011． 294-299

[13] 刘华平，孙富春，何克忠等． 奇异摄动控制系统:理论与应用． 控制理论与应用，2003，20(1)：1-7

[14] 刘业超，刘伊威，刘宏． 柔性关节机器人奇异摄动控制． 电机与控制学报，2009，13(3)：436-441

[15] Spong M W． Modeling and control of elastic joint robots．JournalofDynamicSystemsMeasurement&Control，1987，109(4)：310-319

[16] Makkar C，Dixon W E，Sawyer W G，et al． A new continuously differentiable friction model for control systems design． In：Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics，Piscataway， USA， 2005．600-605

[17] 陈志勇，陈力． 漂浮基带柔性铰空间机器人的动力学建模及奇异摄动控制研究． 中国机械工程，2011，22(18)：2151-2155

[18] Ljubomir T． Grujic． Uniform asymptotic stability of non-linear singularly perturbed general and large-scale systems．InternationalJournalofControl，1981，33(3)：481-504

[19] Spong M W． Adaptive control of flexible joint manipulators： comments on two papers．Automatica，1995，31(4)：585-590

[20] Zheng Q，Gao L Q，Gao Z． On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics． In：Proceedings of the 46th IEEE Conference on Decision and Control，New Orleans，USA， 2007. 3501-3506

[21] 陈启军． 宏-微机器人系统及其轨迹控制研究：[博士学位论文]． 上海：同济大学电子与信息工程学院，1999

[22] Corless M． Guaranteed rates of exponential convergence for uncertain systems．JournalofOptimizationTheory&Applications，1990，64(3)：481-494

[23] 刘福才，高静方，贾晓菁． 考虑重力影响的柔性关节空间机械臂任务空间神经网络控制． 宇航学报，2015，36(12)：1391-1397

Simulation study of the singular perturbation based active disturbance rejection control for flexible joint space manipulators

Liu Fucai， Li Qian， Liu Lin

(Key Lab of industrial Computer Control Engineering of Hebei Province， Yanshan University， Qinhuangdao 066004)

A singular perturbation based active disturbance rejection control method considering friction，nonlinear joint stiffness and external disturbance was proposed for control of flexible joint manipulators under different gravity environments. Firstly， the dynamic model of flexible joint manipulators under the gravity environment and that under the microgravity environment were established． Then， the system model was divided into the fast subsystem and the slow subsystem with the singular perturbation method, and the speed feedback control law was designed to suppress the vibration of flexible joints for the fast subsystem while the active disturbance rejection controller (ADRC) with a feedforward compensation was designed for the slow subsystem to resist the internal and external disturbance． Also， the system stability was analyzed． Finally， the designed controller was verified by simulation and was compared with other control methods． The simulation results show that with the designed controller, the good performance in trajectory tracking and vibration suppression both on the ground and in the space can be achieved, and the internal and external disturbance can be resisted, making the system robust．

space manipulator， flexible-joint， gravity, singular perturbation， active disturbance rejection control

10.3772/j.issn.1002-0470.2016.06.007

①863计划(2012AA)，国家自然科学基金青年基金项目(51605415)和河北省自然科学基金(F2015203362， F2016203494)资助项目。

2016-03-31)

②男，1966年生，博士生导师；研究方向：空间机构运动行为分析与控制技术研究；联系人，E-mail: lfc@ysu.edu.cn