含直觉模糊数的物流供应链合作伙伴优选

刘家财，赵文健，李正红

（1.福建农林大学交通与土木工程学院，福建福州350002；2.福建农林大学金山学院，福建福州350002)

含直觉模糊数的物流供应链合作伙伴优选

刘家财1，赵文健2，李正红1

（1.福建农林大学交通与土木工程学院，福建福州350002；2.福建农林大学金山学院，福建福州350002)

为了更加真实地反映物流供应链合作伙伴选择中出现的模糊不确定性，首先，将无法用精确实数表示的物流供应链合作伙伴评价值用语言变量和直觉模糊数表示，通过语言变量与三角形直觉模糊数之间的转化关系，将语言变量评价值转化为三角形直觉模糊数；然后，基于TOPSIS法和波达选择函数，给出评价值包含三角形直觉模糊数的多目标多人决策方法；最后，用物流供应链合作伙伴优选的数学算例验证该方法的有效性。结果表明，该方法能很好地解决物流供应链合作伙伴优选过程中评价指标的评价值无法用精确实数表示及多人参与决策时决策者的权重缺失的问题。

合作伙伴；三角形直觉模糊数；多目标多人决策；TOPSIS法；波达选择函数

合理选择合作伙伴并建立长期、稳定、友好的合作关系是物流供应链纵向合作顺利开展的关键所在。国内外诸多学者运用逼近于理想解的排序方法 (Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS) 等多属性决策方法，针对物流供应链合作伙伴的优选、信息的共享及模式的演化等问题做了大量研究。例如，肖蕾等[1]运用层次分析法 (Analytic Hierarchy Process，AHP)、网络分析法 (Analytic Network Process，ANP) 等方法对选择供应商时面临的风险程度进行研究；刘中艳等[2]综合运用模糊综合评判法和TOPSIS 法，构建供应商评价指标体系并且研究供应商的优选问题；吴双晶等[3]探讨武夷山无水港物流供应链管理的模式，并给出相应的优化建议和措施；李明等[4]基于数据挖掘技术，对物流供应链合作伙伴的选择问题进行研究，并给出具体求解步骤和流程；徐鑫[5]针对时间敏感客户的混合延迟策略进行研究，探讨混合延迟策略最优的条件。LI D F 等[6]将 TOPSIS 法进一步拓展，用于求解直觉模糊环境下的多属性群决策问题。但是，上述研究多在清晰环境下开展，即选用精确实数表示决策值，而由于在选择供应链合作伙伴时，系统自身错综复杂、不确定因素较多，导致节点企业之间的合作回报周期长、资金投入大、风险预估困难、利润很难达到预计期望，因而无法用精确的数值具体描述某一评价指标。例如，某铁路物流合作企业期望所得利润“不少于 3 千万元”，产品开发周期“需1 个月的概率为 80%、需 20 天的概率为 30%”。为了将这些模糊数值表达得更加清楚，选用直觉模糊数表示决策者对某一评价指标的评价值，以便于描述模糊数值的大致范围，同时反映决策者对其所做判断和估计的犹豫度。

1　含直觉模糊数的物流供应链合作伙伴优选理论

1.1相关概念及定义

（1）直觉模糊集。模糊集是模糊集理论的基本概念之一[7-8]，1965 年由 ZADEH L A[9]提出，是解决模糊性的一种有效方法[10-11]。1983 年，ATANASSOV K T[12-13]提出直觉模糊集的概念，其实质是利用 2 个并非完全独立的标度，分别刻画对象 “属于”与“不属于”模糊概念 的程度。显然，具有 2 标度特征的直觉模糊集能更细腻、有效地刻画模糊性。

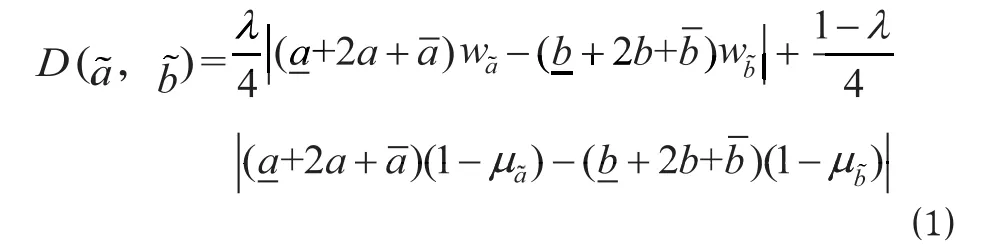
1.2含直觉模糊数的混合多属性决策的数学表示

由 p 个决策者 Pk(k = 1，2，…，p) 组成的决策群体记为 P ={P1，P2，…，Pp}，该决策群体对 n 个方案 xj( j = 1，2，…，n) 的 m 个属性oi(i = 1，2，…，m) 进行评价，记方案集 X ={x1，x2，…，xn}，属性集 O ={o1，o2，…，om}。假设决策者 Pk对方案 xj∈ X 的属性 oi∈ O 的评价值可用三角形直觉模糊数， m；j = 1，2，…，n) 来表示，该三角形直觉模糊数表明模糊数量可用介于和之间的任意实数表示，且每个实数都具有不同的隶属度和非隶属度。更确切地说，表示决策者 Pk认为的方案 xj的属性 oi的最可能的值，其隶属度与非隶属度分别为和分别表示决策者 Pk认为的方案 xj的属性 oi的最不可能的最小值和最大值，其隶属度与非隶属度分别为 0 和 1。决策者Pk对方案 xj的所有 m 个属性的评价值可用向量的形式表示为

假设集合 B、集合 C 分别为效益型属性和成本型属性下标的集合，为消除物理量纲及因属性类型的不一致性对决策结果的影响，通常利用公式 ⑶ 和公式 ⑷ 将三角形直觉模糊数决策矩阵进行规范化处理。

2　含三角形直觉模糊数的混合　TOPSIS　法

用语言变量表示决策者 Pk(k = 1，2，…，p) 给出的属性的重要程度，结合三角形模糊数与三角形直觉模糊数的关系，即三角形模糊数是其对应的三角形直觉模糊数当最大隶属度为 1、最小非隶属度为 0 时的特殊情况，假设语言变量与三角形直觉模糊数的对应关系如表1 所示[16-17]。

表1　语言变量与三角形直觉模糊数之间的对应关系

用语言变量描述决策者 Pk(k = 1，2，…，p) 给出的属性 oi(i = 1，2，…，m) 的权重，将其转化为相应的三角形直觉模糊数。其中，表示决策者 Pk认为的属性 oi的最可能的权重值，其隶属度与非隶属度分别为 1 和 0；和分别表示决策者 Pk认为的属性 oi的最不可能的最小权重值和最大权重值，其隶属度与非隶属度分别为 0 和 1。决策者 Pk(k = 1，2，…，p) 给出的所有属性 oi(i = 1，2，…，m) 的权重可用向量表示为

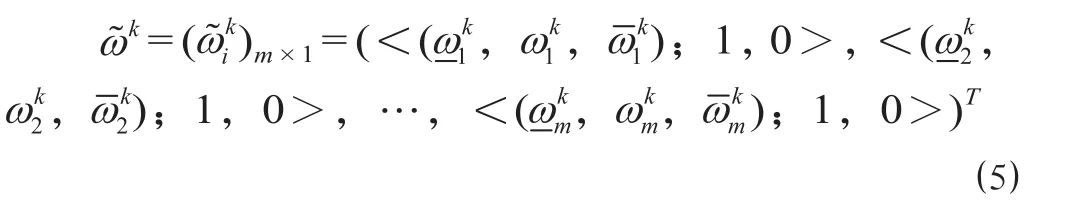
将属性值作为三角形直觉模糊数的决策矩阵进行规范化处理，得到决策矩阵(k = 1，2，…，p)；利用三角形直觉模糊数表示的权重向量，采用线性加权的方法，得到决策者 Pk的属性值为三角形直觉模糊数的加权决策矩阵(k = 1，2，…，p)，即

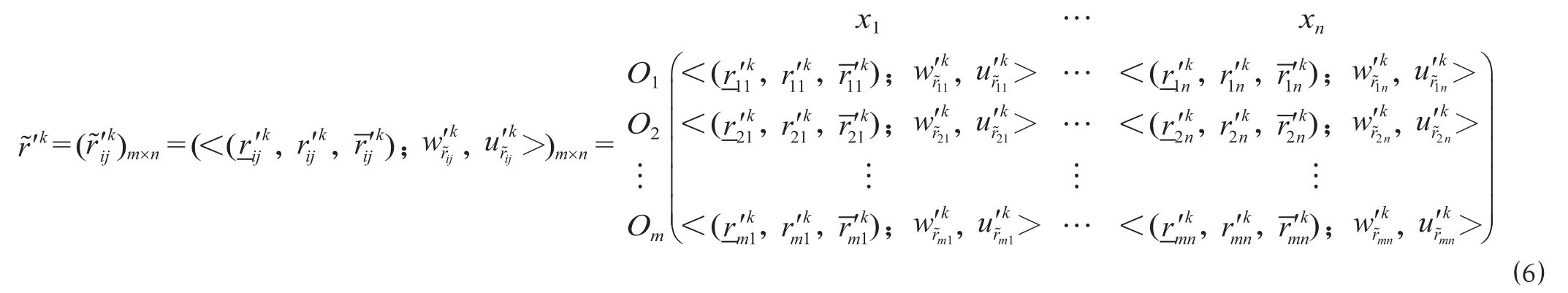
决策者 Pk的三角形直觉模糊数正理想解和负理想解分别为

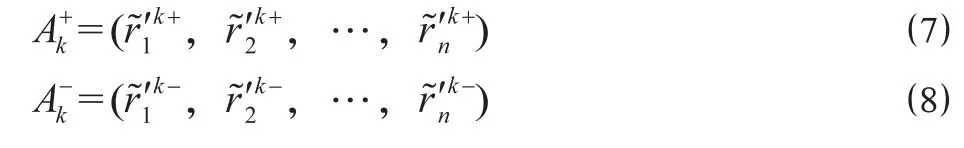
其中，

决策者 Pk关于方案 xj与三角形直觉模糊数正理想解和负理想解的距离分别为

由公式 ⑾、公式 ⑿ 可得决策者 Pk关于方案 xj与三角形直觉模糊数正理想解的相对接近度为

3　案例研究

物流供应链是指围绕原材料的采购、产品的生产、产品的销售这 3 个环节所开展的物流活动所形成的有机链条，通常包含物流服务提供商、供应商、制造商、分销商、零售商、最终用户等多个主体。物流供应链合作伙伴的优劣会直接影响整个供应链系统的绩效和竞争力，应当采取科学、系统的方法对物流供应链合作伙伴的选择问题进行研究。假定现有 3 个决策者 P1，P2，P3组成决策专家组对物流供应链系统中的 3 家物流服务提供商进行评价，3 家物流服务提供商分别用方案 xj( j = 1，2，3) 来表示。经过分析和论证，选取企业规模 (o1)、企业信誉 (o2)、产品价格 (o3/元)、准时交货率 (o4)、响应时间 (o5/h) 等 5 个方面作为优选物流供应链合作伙伴的评价指标。由于每个决策者的教育背景、学识经验、喜好偏向等方面存在差异，导致各决策者对 5 个评价指标重要性的评价值有所不同。为了更加真实地描述每个决策者认为的各评价指标的重要程度，使用“非常不重要、很不重要、较不重要、一般、较重要、很重要、非常重要”7 级语言变量集表示评价指标的重要程度，如表2 所示。

表2　决策者给出的 5 个评价指标的重要程度

用语言变量和三角形直觉模糊数来表示各决策者 Pk(k = 1，2，3) 给出的物流服务提供商各个评价指标的评价值。利用问卷调查方法对所得结果进行统计，得到各决策者 Pk(k = 1，2，3) 认为的各物流服务提供商即方案 xj( j = 1，2，3) 关于属性 oi(i = 1，2，3，4，5) 的评价值，具体结果如表3 所示。

将用语言变量表示的物流服务提供商评价指标的评价值转化为相应的三角形直觉模糊数，利用公式 ⑶ 和公式 ⑷ 对三角形直觉模糊数决策矩阵进行规范化，得到规范化决策矩阵如下。

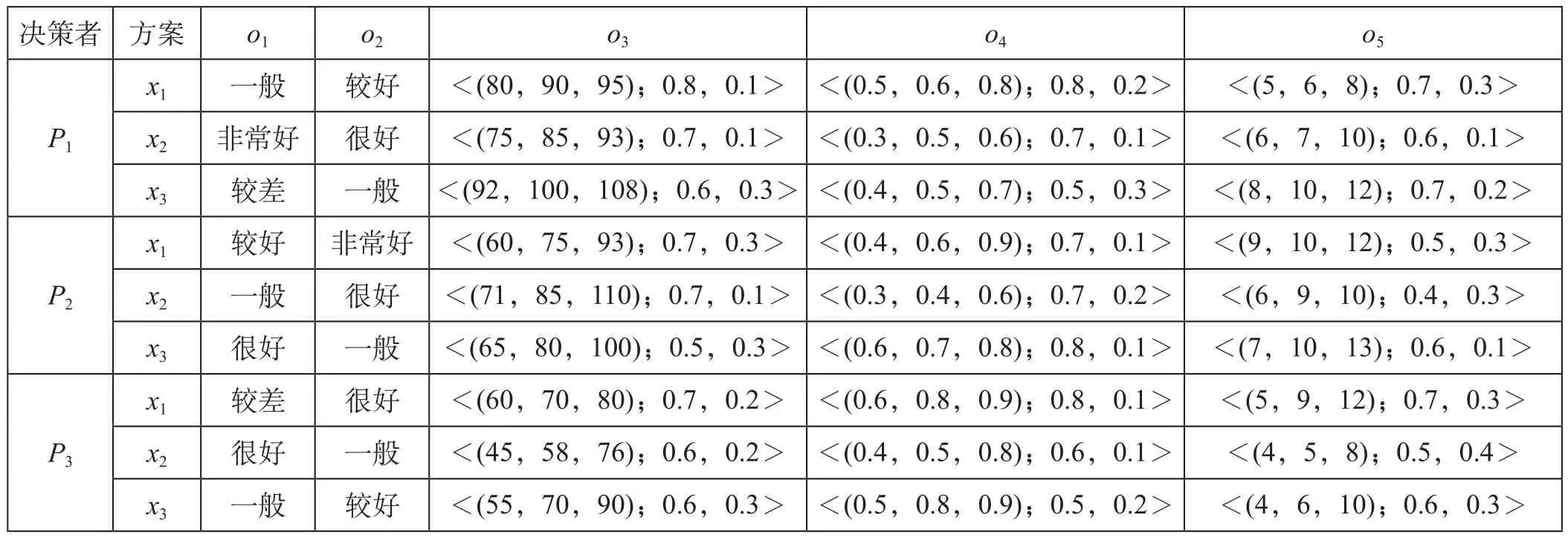
表3　决策者 P1，P2，P3关于 3 个备选方案中各个指标的评价值

将决策者 P1给出的 5 个评价指标的重要性程度转化成相应的三角形直觉模糊数，得到如下的三角形直觉模糊数权重向量

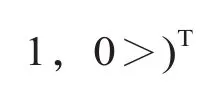
根据公式 ⑺ 和公式 ⑻ 得到决策者 P1给出的物流服务提供商的三角形直觉模糊数正理想解和负理想解分别为

取 λ= 5，根据公式 ⑾ 和公式 ⑿ 得到决策者 P1关于第 1 家物流服务提供商即方案 x1与正理想解的距离，关于第 1 家物流服务提供商即方案 x1与负理想解的距离。同理可得，决策者 P1关于第 2 家物流服务提供商即方案 x2、第3 家物流服务提供商即方案 x3与其正、负理想解的距离分别为：，。

根据公式 ⒀，分别计算决策者 P1关于各物流服务提供商即方案 xj( j = 1，2，3) 与三角形直觉模糊数正理想解的相对接近度，结果为：。因为，所以决策者 P1给出的各物流服务提供商即方案 xj( j = 1， 2，3) 的优劣顺序为： x2≻x1≻x3。同理，分别得到决策者 P2关于各物流服务提供商即方案 xj( j = 1， 2，3) 与三角形直觉模糊数正理想解的相对接近度，以及 P3关于各物流服务提供商即方案 xj( j = 1， 2，3) 与三角形直觉模糊数正理想解的相对接近度，结果为：0.51，。可以看出，决策者 P2给出的各物流服务提供商即方案 xj( j = 1，2，3) 的优劣顺序为： x3≻x1≻x2，而决策者 P3给出的各物流服务提供商即方案 xj( j = 1，2，3) 的优劣顺序与 P1相同，即， x2≻x1≻x3。再通过波达选择函数方法[10]，得到 3 个决策者组成的决策群体赋予各物流服务提供商即方案 xj( j = 1，2，3) 的波达选择函数值分别为： b (x1) = 3，b (x2) = 4，b (x3) = 2。

综上所述，决策群体对 3 家物流服务提供商即3 个备选方案给出的优劣排序为x2≻x1≻x3，即物流服务商 2 最优，物流服务商 1 次之，物流服务商 3 最差。

4　结束语

物流供应链是从市场的需求或服务的需求开始，到满足需求为止的整个过程中所涉及到的物流活动所形成的链条。物流供应链主要包含原材料的采购、产品的生产、产品的销售 3 部分，在这些环节通常会涉及很多的物流活动。物流供应链管理对于企业降低成本、优化流程、分散风险等方面都具有重要的作用。因此，选择合适的物流供应链合作伙伴有助于提升整条供应链的核心竞争力。为了更真实地反映出决策者情况，通过运用混合多属性决策的基本原理和方法，基于混合 TOPSIS 法和波达选择函数，构建多目标多人决策模型，将其应用于解决物流供应链合作伙伴优选的实例中，结果表明，该方法能够较好地处理物流供应链合作伙伴优选过程中存在的模糊信息，在很大程度上避免了评价信息的失真，使决策结果更为客观、真实，为解决直觉模糊环境下的物流供应链合作伙伴优选问题提供了一种新的研究视角和解决方案。由于模糊环境下的评价值很多，包括区间值、直觉模糊数、直觉模糊集等，因而可以将基于TOPSIS 法的混合多属性决策模型与方法拓展到其它模糊环境，为复杂环境下的物流供应链合作伙伴优选问题提供全新、高效率的解决方案。

[1] 肖 蕾，王 铁. 企业采购风险定量测度方法[J]. 铁道运输与经济，2010，32(7)：6-10.

XIAO Lei，WANG Tie. Quantitative Measure Method of Enterprise Purchase Risk[J]. Railway Transport and Economy，2010，32(7)：6-10.

[2] 刘中艳，陈 娟. 基于 FAHP-TOPSIS 的医疗设备制造企业供应商选择研究[J]. 湖南工业大学学报，2015，7(4)：90-95.

LIU Zhong-yan，CHEN Juan. Study on Supplier Selection of Medical Equipment Enterprises based on FAHP-TOPSIS[J]. Journal of Hunan University of Technology，2015，7(4)：90-95.

[3] 吴双晶，王 莹，陈 颐. 构建武夷山无水港物流供应链的研究[J]. 商业经济，2014(12)：47-48. WU Shuang-jing，WANG Ying，CHEN Yi. To Build a Dry Port Logistics Chain in Wuyishan[J]. Commercial Research，2014(12)：47-48.

[4] 李 明，姚远耀. 数据挖掘技术在物流供应链合作伙伴选择中的应用[J]. 物流技术，2015，34(2)：152-154.

LI Ming，YAO Yuan-yao. Research on Application of Data Mining Technology in Partner Selection in Logistics Supply Chains[J]. Logistics Technology，2015，34(2)：152-154.

[5] 徐 鑫. 延迟策略在物流供应链中的应用[J]. 安徽大学学报(自然科学版)，2012，36(3)：29-36.

XU Xin. An Application of Postponement Strategy in Supply Chains[J]. Journal of Anhui University (Natural Science Edition)，2012，36(3)：29-36.

[6] LI D F，NAN J X. Extension of the TOPSIS for Multi-Attribute Group Decision Making under Atanassov IFS Environments[J]. International Journal of Fuzzy System Applications，2011，1(4)：47-61.

[7] WANSP，WANG Q Y，DONGJY. The Extended VIKOR Method for Multi-Attribute Group Decision Making with Triangular Intuitionistic Fuzzy Numbers[J]. Knowledge-Based Systems，2013，52(6)：65-77.

[8] LI D F. Multiattribute Decision Making Method based on Generalized OWA Operators with Intuitionistic Fuzzy Sets[J]. Expert Systems with Applications，2010，37(12)：8673-8678.

[9] ZADEH L A. Fuzzy sets[J]. Information and Control，1965，8(3)：338-353.

[10] 李登峰. 模糊多目标多人决策与对策[M]. 北京：国防工业出版社，2003.

LI Deng-feng. Fuzzy Multiobjective Many-Person Decision Makings and Games[M]. Beijing：National Defense Industry Press，2003.

[11] 黄宪成. 模糊多目标决策理论、方法及其应用研究[D]. 大连：大连理工大学，2003.

[12] ATANASSOV K T. Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems，1986，20(1)：87-96.

[13] ATANASSOV K T. Intuitionistic Fuzzy Sets[M]. Heidelberg：Springer-Verlag，1999.

[14] 张茂军，南江霞，李登峰，等. 带有三角直觉模糊数的多属性决策的 TOPSIS[J]. 运筹与管理，2012，21(5)：96-101.

ZHANG Mao-jun，NAN Jiang-xia，LI Deng-feng, et al. TOPSIS for MADM with Triangular Intuitionistic Fuzzy Numbers[J]. Operations Research and Management Science，2012，21(5)：96-101.

[15] 李登峰. 直觉模糊集决策与对策分析方法[M]. 北京：国防工业出版社，2012.

LI Deng-feng. Intuitionistic Fuzzy Set Decision and Game Analysis Methodologies[M]. Beijing：National Defense Industry Press，2012.

[16] CHEN C T. Applying Linguistic Decision-Making Method to Deal with Service Quality Evaluation Problems[J]. International Journal of Uncertainty，Fuzziness and Knowledgebased Systems， 2011，9(1)：103-114.

[17] 李 帅，郭亚军，易平涛，等. 基于模糊群决策的虚拟企业合作伙伴选择[J]. 东北大学学报(自然科学版)，2004，25(3)：295-298.

LI Shuai，GUO Ya-jun，YI Ping-tao，et al. Partner Selection based on Fuzzy Group Decision-Making for Virtual Enterprise Formation[J]. Journal of Northeastern University(Natural Science)，2004，25(3)：295-298.

责任编辑：金艳萍

[3] 徐 茜，黄祖庆. 区域物流与区域经济发展互动关系研究：以浙江省为例[J]. 统计与决策，2011(9)：116-119.

[4] 郭 艳，于兆宇. 江西区域物流能力与经济系统协同发展[J]. 企业经济，2012 ，31(11)：124-127.

[5] 高文相，吕 宏. 基于经济产业结构的大理州物流需求研究[J]. 铁道运输与经济，2015，37(7)：11-15.

GAO Wen-xiang，LV Hong. Study on Logistic Demand in Dali based on Economic Industry Structure[J]. Railway Transport and Economy，2015，37(7)：11-15.

[6] 魏权龄，卢 刚. DEA 方法与模型的应用：数据包络分析(三) [J]. 系统工程理论与实践，1989 (3)：67-75.

[7] 常 爽，张芳芳. 物流能力理论综述[J]. 中国市场，2012(28)：27-29.

[8] 黄 彦. 基于 ARIMA 模型的我国社会消费品零售总额实证分析[J]. 经济论坛，2011(11)：31-37.

[9] 张文学，张东华，钟 江，等. 铁路物流综合管理系统的研发[J]. 铁道货运，2014，32(11)：1-7.

ZHANG Wen-xue，ZHANG Dong-hua，ZHONG Jiang，et al. Research and Development of Railway Logistic Comprehensive Management System[J]. Railway Freight Transport，2014，32(11)：1-7.

责任编辑：李琨浩

The Selection of Logistics Supply Chain Cooperators by Evaluation Values with Intuitionistic Fuzzy Numbers

LIU Jia-cai1, ZHAO Wen-jian2, LI Zheng-hong1

(1.School of Transportation and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou 350002, Fujian,China; 2.School of Jinshan, Fujian Agriculture and Forestry University, Fuzhou 350002, Fujian,China)

In order to reflect more realistically the fuzziness and uncertainty, linguistic variables and intuitionistic fuzzy numbers are usually used to express the evaluation values in the process of logistics supply chain cooperator selection. In this paper, Firstly, the connection between linguistic variables and triangular intuitionistic fuzzy numbers is given, and linguistic variables of logistics supply chain cooperator selections are transformed into triangular intuitionistic fuzzy numbers according to certain relationship. Moreover, based on the TOPSIS method and the Borda choice function, one model is proposed for solving multi-objective many-person decision making problems whose attribute values include triangular intuitionistic fuzzy numbers. Finally, a mathematical calculation about the selection of logistics supply chain cooperator is given to exemplify its applications. The proposed method can be applied to the problem of logistics supply chain cooperator selection where the evaluation values are not suitable to be expressed with real numbers. Moreover, it can efficiently solve the decision making problems which are lacking in the weight of decision makers.

Partner; Triangular Intuitionistic Fuzzy Number; Multi-Objective Many-Person Decision Making; TOPSIS Method; Borda Choice Function

1003-1421(2016)11-0041-07

F259.27

A

10.16668/j.cnki.issn.1003-1421.2016.11.09

2016-08-16

福建省中青年教师教育科研项目(JA13122)；福建省软科学研究计划项目(2016R0012)；国家社会科学基金项目(13BGL150)

2016-04-20

2016-09-25

国家社会科学基金资助项目 (15BGL014)