电感耦合等离子体测定水系沉积物中铜的标准曲线的不确定度的评定

■杨静

（甘肃省第四地质矿产勘查院实验室　甘肃　酒泉　735000）

电感耦合等离子体测定水系沉积物中铜的标准曲线的不确定度的评定

■杨静

（甘肃省第四地质矿产勘查院实验室甘肃酒泉735000）

采用对水系沉积物中铜的标准曲线中标准点配制的不确定度的评定和标准曲线拟合的不确定度的评定两个方面来评定水系沉积物中铜的不确定度。结果表明水系沉积物中铜元素含量越低不确定度越大，并且标准曲线拟合过程引入的不确定度是水系沉积物中铜元素不确定度的主要表现，这与试验室实际测试过程中的情况相吻合。

铜水系沉积物不确定度评定

根据ISO/IEC17025-2005《测试和校准实验室能力的一般要求》[1]的规定。测数据的报告必须包括评估测量不确定度的相关信息。随着中国实验室国家认可委员会(CNAS)认可要求[2]，建立测量的不确定度的评定程序，对测量方法、测量结果进行不确定度评定是测试实验室质量保证和质量控制不可或缺的信息[3]，也是对测试仪器、方法重现性的一种评价，这种可以减少实验过程中误差的形成，尽量使得不确定度变小，在一定的置信度下。

1　实验部分

1.1仪器及试剂

icap-Qc电感耦合等离子体质谱仪盐酸硝酸氢氟酸高氯酸试验用水均为去离子水，电阻率。

1.2标准溶液的配制

Cu的标准系列溶液:向一系100ml容量瓶中分别加入0.00、0.10、0.50、1.00、5.00、10.00ml的Cu标准使用溶液，用3%的HNO3定容至刻度。

2　标准使用溶液配制过程中的的不确定度

标准使用溶液的不确定度评定属于B类评定，一般不需要对被测量仪器在统计控制状态下进行重复观测，而是按照现有的信息加以评定。

2.1铜标准溶液（100ug/ml）配制及不确定度

用10ml（A级）单标线移液管移取10.0ml1000ug/ml铜标准储备溶液于100ml（A级）容量瓶中，用1%的HNO3稀释至标线，摇匀，得到浓度为100ug/ml的铜标准中间溶液。

（1）标准储备溶液的浓度ρ0的不确定度为0.0035

（2）移取标准储备溶液体积V0的不确定度

10ml单标移液管的重复性标准不确定度为0.01ml

20℃时10ml单标移液管示值允值±0.020ml，假设为三角分布，温度误差引起的不确定度为0.0105ml.

假设为均匀分布,因此体积引起的不确定度为0.00143

（3）标准中间溶液的定容体积V1的不确定度为0.001198

（4）铜标准溶液（100μg/ml）不确定度为0.3966

根据上述评定中间溶液（1）的浓度为100±0.80（K=2）

2.2铜标准溶液（10μg/ml）配制及不确定度

用10ml（A级）单标线移液管移取10.0ml100μg/ml铜标准储备溶液于100ml（A级）容量瓶中，用1%的HNO3稀释至标线，摇匀，得到浓度为10μg/ml的铜标准中间溶液。同（2.1）可知铜标准溶液（10μg/ml）不确定度为0.04383ug/ml。

根据上述评定标准中间溶液（2）的浓度为10±0.080（K=2）

2.3铜标准溶液（1μg/ml）配制及不确定度

用10ml（A级）单标线移液管移取10.0ml10μg/ml铜标准储备溶液于100ml（A级）容量瓶中，用1%的HNO3稀释至标线，摇匀，得到浓度为1μg/ml的铜标准中间溶液。

根据2.1可知铜标准溶液（1μg/ml）不确定度为0.004383ug/ml

根据上述评定标准中间溶液（2）的浓度为1.00±0.01（K=2）

2.4标准系列溶液的不确定度

向一系列 100ml容量瓶中分别加入 0.00、0.10、0.50、1.00、5.00ml、10ml的Cu标准使用溶液，均用3%的HNO3稀释至标线，摇匀，即得到浓度分别为0.00、1.00、5.00、10.00、50.00、100.00ng/ml的Cu的标准溶液。

计算出标准系列的不确定度如下表1。

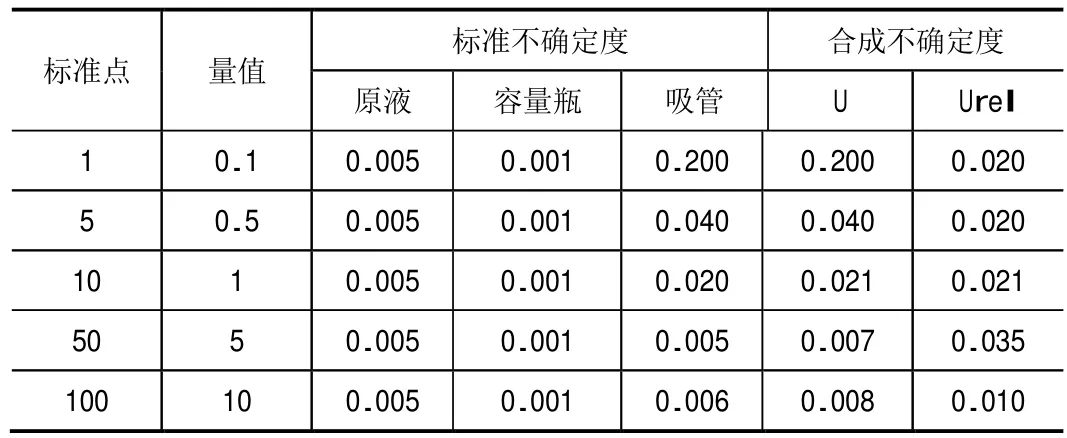
表1　标准溶液的不确定度

2.5曲线拟合过程中的不确定度分析

采用不确定度连续传递模型[5-6]，在xi、dxi、yi、dyi四组数据的基础上，考虑到标准点的不确定度对拟合曲线的影响，以x、y的相对误差为权重进行双误差曲线回归得到曲线方程为：y=27868.779x﹢3735.580， 其 中 R2=1.000，a=27868.779±88.817,b=3735.580± 0.500。而对于任一标准点系列的测量值yi，可以通过回归曲线方程，得到各点的回归值xc和曲线拟合过程引入的标准不确定度。

2.6样品合成标准不确定度

对于上述任一测量点，其标准不确定度的估计可由下式计算：

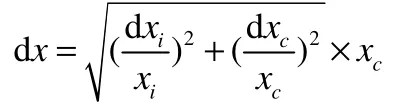
式中，xi-xc；yi=yc；dxi—用线性插值算的处的不确定度；dyi—用线性插值算的yc处的不确定度；dxi/xi—由标准配制所引入的相对标准不确定度；dxc/xc—由拟合及计算过程所引入的相对不确定度；dx—合成标准不确定度。对于标准曲线范围内任一次测量，可以根据上述公式求得标准不确定度的估计值。例如某一水系沉积物中Cu元素的3次测量结果分别是：772288、770695、775587，可以计算得出Y=772856，回归得到：x=98.372，利用公式计算得出dxc=1. 022。用插值法算出dx=0.0285，因此：u=1.87

若扩展因子取2，则结果的95%置信区间为(32.37±1.05)μg/g。

3　结语

采用x,y的相对差，对标准曲线进行双误差回归，结果表示在含量越低的样品测试的不确定度越大，并且曲线拟合过程中是铜元素的主要表现形式，这与实际测试过程中的情况相符合，在实际样品测试过程中选择合适的标准曲线点对测试结果非常重要。

[1]ISO/IEC17025-2005，测试和校准实验室能力的一般要求 [S].

[2]国家质量技术监督局计量司.测量不确定度评定与表示指南 [M].北京：中国计量出版社，2000：89.

[3]凌进中.地质标准物质中痕量元素量值溯源性探讨 [J].岩矿测试，2000，19（3）：188-193.

F407.1[文献码]B

1000-405X（2016）-9-219-1