基于仿射不变线矩和改进关联度分析的水电机组轴心轨迹自动识别研究

刘海艳，郑慧娟，刘 果

（国网电力科学研究院/南京南瑞集团公司，江苏省南京市 210003）

基于仿射不变线矩和改进关联度分析的水电机组轴心轨迹自动识别研究

刘海艳，郑慧娟，刘 果

（国网电力科学研究院/南京南瑞集团公司，江苏省南京市 210003）

本文考虑到图形的非相似变换，选用仿射不变线矩作为轴心轨迹特征提取方法，结合一种改进的灰色关联度分析方法，给出了一种水电机组轴心轨迹自动识别新方案。本文通过MATLAB仿真了5种常见转子振动故障对应的轴心轨迹和5个待识别的图形，提取其仿射不变线矩，通过计算参考模式和待识别模式之间的关联度，将待识别图形正确分类，验证了新方案显著的识别效果。

轴心轨迹；仿射不变线矩；灰色关联度分析

0 引言

水电机组的轴心轨迹可直观地显示转子实际运动情况，其图形特征与转子振动故障之间有着直接或者间接的对应关系。例如，转子质量不平衡故障引起的轨迹图形为椭圆形；转子不对中故障引起轨迹图形为香蕉形或者外“8”字形；油膜涡动故障引起的轨迹图形为内“8”字形；碰摩故障对应的轴心轨迹形状为规则或者不规则的花瓣形等。对轴心轨迹形状进行研究，可了解机组运行信息，及时发现振动故障，合理安排检修以保障机组安全运行[1]。

轴心轨迹形状自动识别的研究对于机组故障诊断自动化至关重要。1962年，M.K.Hu在文献[2]中提出了满足平移、旋转、比例缩放不变性的7个不变矩函数，并在图像识别领域得到了广泛应用。然而，HU氏不变矩作为特征提取方法，只对作相似变换的图形有效，这就限制了HU氏不变矩在轴心轨迹自动识别研究中的应用。1993年，Jan Flusser与Tomas Suk提出了图像在仿射变换下保持不变的仿射不变矩[3]。

本文提出了一种仿射不变线矩与灰色关联度分析相结合的自动识别方法，可实现图形在作斜变换等非相似变换下的正确识别。

1 仿射不变线矩

1.1 仿射变换

二维图形的仿射变换如下：

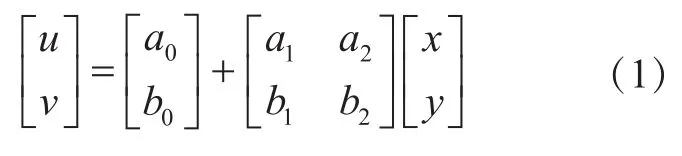
如下6种变换可以替代式（1）：

平移变换：

伸缩变换：

斜切变换：

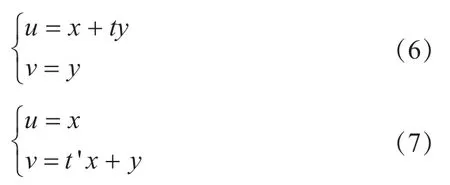
矩阵F在变换（1）下保持不变，等价于在变换（2）～（7）下保持不变[4]。

1.2 仿射不变线矩

平面轴心轨迹曲线c=c[x（t），y（t）]的（p+q）阶矩定义为：

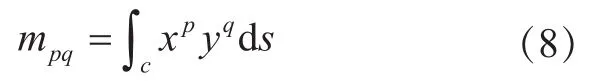
（p+q）阶中心矩定义为：

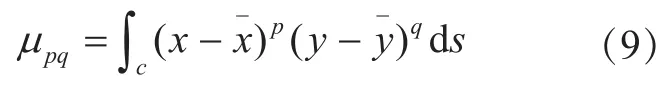
对μpq进行归一化处理得到ηpq：

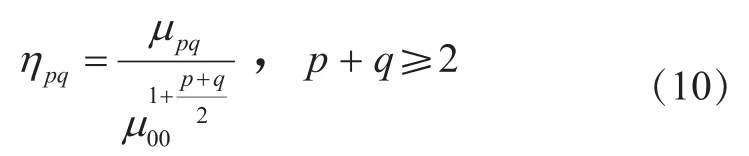
单一的矩阵往往不能进行有效识别。HU将归一化的中心矩线性组合，构造了具有平移、旋转、比例缩放不变性的7个矩函数。然而HU氏不变矩只在图形发生平移、旋转、缩放等相似变换下保持不变，若图形发生非对称比例变换或者斜变换等非相似变换，HU氏不变矩将发生改变。

仿射不变矩可以满足非相似变换的要求。仿射不变矩由HU构造的中心矩转化而来的。

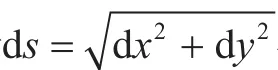
由于积分因子非线性，为了消除这种影响，重新定义积分因子如下：

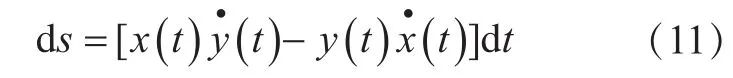
则几何矩变为：

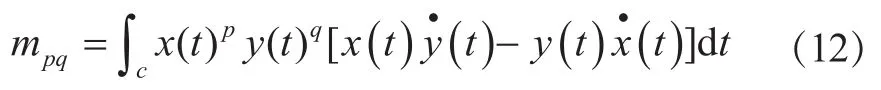
中心矩变为：

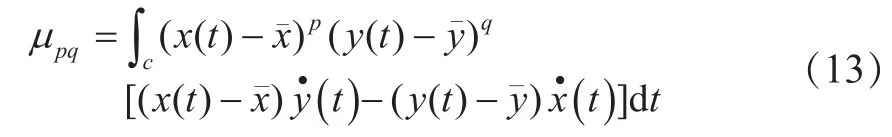
为了计算方便，微分项可用式（14）替代：

满足变换（2）～（7）的仿射不变线矩可通过Apolar法、Hankel行列式法、多项式判别式法等方法构造[5]。由于高阶矩的计算量太大，本文选用前三阶矩组合成的如下仿射不变线矩作为特征量：

取对数进行数据压缩：

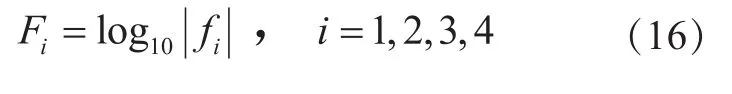
2 仿真试验

2.1 参考模式的建立

根据下面的参考公式[6]，在MATLAB中模拟出几种常见故障对应的轴心轨迹：

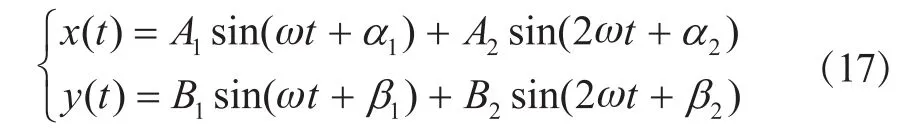
其中，x（t）和y（t）分别为仿真轴心轨迹图形x向和y向坐标，ω是角频率，A1，A2，B1，B2分别为 x（t）和 y（t）的 1、2倍频的幅值，α1，α2，ß1，ß2分别为对应的相位角。通过改变 A1，A2，B1，B2，α1，α2，ß1，ß2这 8个参数值的大小，就可以确定常见的椭圆形、香蕉形、内“8”字形、外“8”字形、花瓣形，如图1所示。

根据式（8）～式（16）计算出图1参考图形的仿射不变线矩，结果见表1。

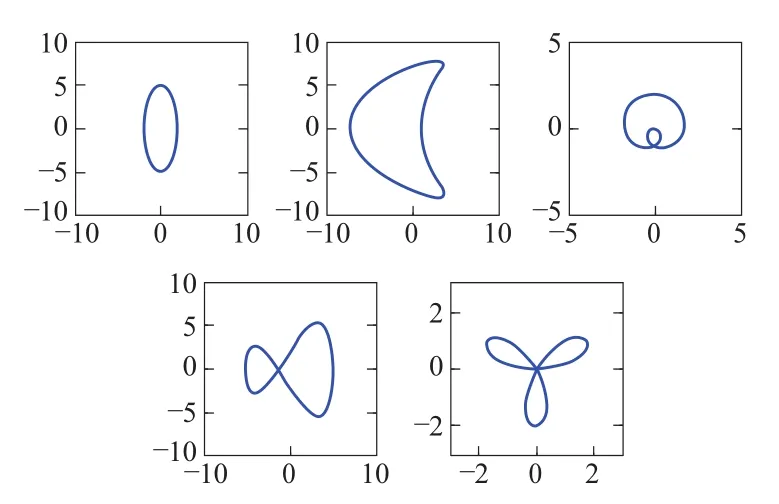
图1 参考图形

表1 参考图形的仿射不变线矩特征向量

实际工程中，每个机组都有自己的特点，轴心轨迹形状千变万化。不同形状的轴心轨迹特征量都不相同。即使是同一故障对应的轴心轨迹，由于初相角、幅值等的不同，图形的变形程度不同，特征量也可能会相差很大。所以，为了提高识别的准确度，参考模式需要结合现场实测数据进行细分并且逐渐丰富，建立尽量多的分类。

2.2 待识别图形特征量计算

将参考图形的特征向量作为标准特征值，待识别图形如图2所示。

图2 待识别图形

同样的，根据式（8）～式（16）计算待识别图形的仿射不变线矩特征向量，结果见表2。

表2 待识别图形的仿射不变线矩特征向量

2.3 基于新型关联度分析方法的形状识别

灰色关联度分析的基本思想是通过确定参考数据列和若干个比较数据列几何形状的相似程度来判断它们之间的联系是否紧密。灰色关联度分析因其计算量小、对样本要求不高等优点在图像识别领域得到广泛应用。但是由于传统的关联度分析是通过求各元素之间关联系数的平均值得到的，分辨率较小。为了提高识别精度，本文采用文献[7]中提出的新型关联度计算方法，实现待识别模式的正确分类。

设L个参考数据序列组成的参考矩阵XC为：

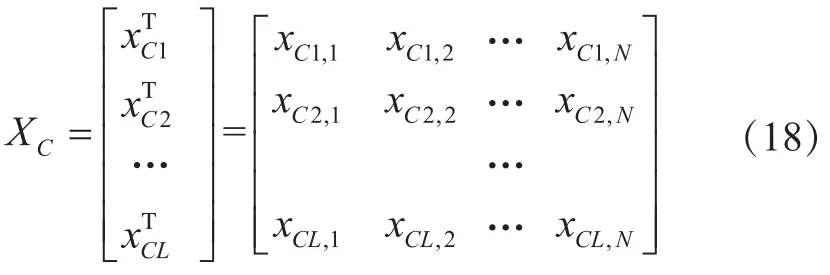
M个待识别数据序列组成的待识别矩阵XD为：

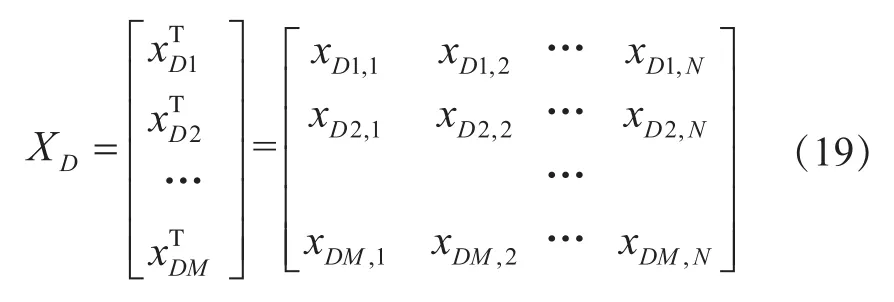
其中，N是特征向量的维数。

则参考模式和待识别模式各元素的关联系数为：

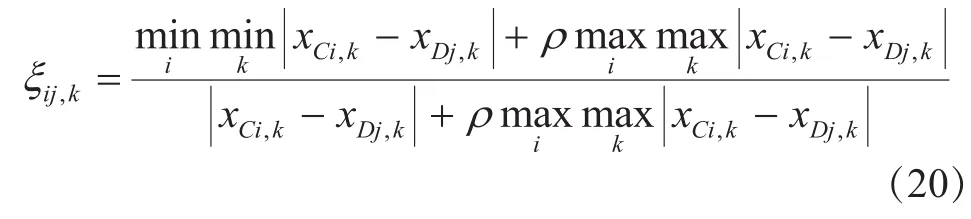
ξij，k为xCi与xDj在第k点的关联系数，分辨系数ρ∈[0，1]，通常取值为0.5。则M个待识别序列与第i个参考序列之间的关联系数矩阵为：

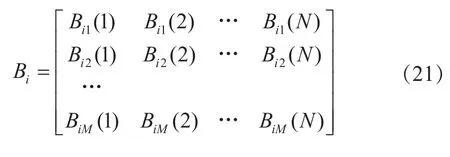
其中，i=1，2，…，L。找到Bi每一列的最大值与最小值，记为：

记关联系数之间最大的距离为：

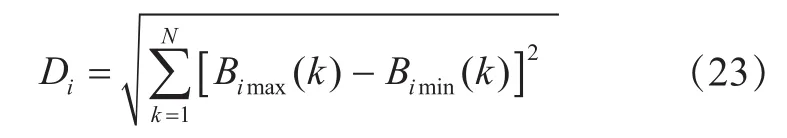
当且仅当每一个关联系数都是最大时，关联度rij才是最大的。

参考图形和待识别图形特征向量的关联度计算如表3所示：

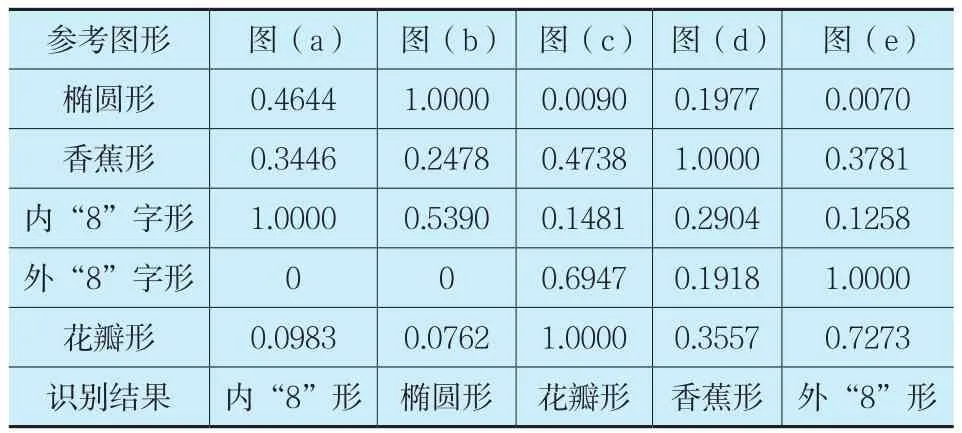
表3 判别类型表

从判别类型表可以看到，同一种类型的仿射不变线矩特征量保持高度一致，采用新型关联度分析作为模式识别方法，待识别图形被正确分类。

3 结束语

考虑到图形存在非相似变换的可能性，本文选用仿射不变矩代替HU式不变矩作为特征提取方法，应用到轴心轨迹自动识别研究中。并且考虑到轴心轨迹是二维曲线图形这一特点，采用线积分代替传统面积分，提出了基于仿射不变线矩和高分辨率关联度分析的轴心轨迹自动识别新方案，仿真了几种水电机组常见振动故障的轴心轨迹图，提取了参考图形和待识别图形的仿射不变线矩特征量，并通过计算两者之间的关联度将待识别图形逐一分类。结果表明，本文提出的轴心轨迹自动识别方案具有很高的工程实用价值。

[1] 万书亭，吴炳胜． 基于改进型不变线矩特征的机组轴心轨迹形状自动识别 [J]． 热能动力工程，2008，23（02）：144-147．

[2] Hu M K． Visual pattern recognition by moment invariant．IEEE Trans on IT， 1962，8（2）： 179-187．

[3] J Flusser， T Suk， Pattern Recognition by Affine Moment invariants[J]． Pattern Recognition． Vol． 26（1）： 167-174．

[4] 付波，周建中，彭兵，等． 基于仿射不变矩的轴心轨迹自动识别方法[J]． 华中科技大学学报（自然科学版），2007，35（03）：119-122．

[5] 李迎春，陈贺新，高磊． 基于仿射不变矩的神经网络目标识别 [J]． 计算机工程，2004，30（02）： 31-32．

[6] 刘刚，李明，乔宝明等． 故障转子系统轴心轨迹的自动识别研究 [J]． 中国测试，2014，40（01）： 110-113．

[7] 万书亭，李和明，李永刚． 基于不变矩特征和新型关联度的轴心轨迹形状自动识别[J]． 热能动力工程，2005，20（3）：239-241，245．

刘海艳（1990—），女，硕士研究生，主要研究方向：水电机组状态监测与智能故障诊断技术研究。E-mail：iamliuhaiyan@163．com

郑慧娟（1982—），女，副高级工程师，主要研究方向：水电厂自动化技术。E-mail：zhenghuijuan@sgepri．sgcc．com．cn

刘 果（1964—），男，高级工程师，主要研究方向：大坝安全监测自动化仪器及系统的研发。E-mail：liuguo@sgepri．sgcc．com．cn

Research on Automatic Identification of Shaft Orbits of Hydropower Units based on Affine Invariant Moments and Improved Gray Correlation Analysis

LIU Haiyan， ZHENG Huijuan， LIU Guo
（State Grid Electric Power Research Institute， Nanjing 210003，China）

Considering the non-similar transformation of shaft orbits， this paper selects the affine invariant moments as the feature vector of the shaft orbit and then presents a new program for automatic identification of shaft orbits combined with an improved method of gray correlation analysis. By MATLAB simulation， 5 kinds of reference shaft orbits， 5 unknown shaft orbits and their feature value can be got. By calculating the gray correlation of the feature data， those unknown shaft orbits could be classified correctly， which verifying the obvious identification effect of the new program.

shaft orbits; affine invariant moments; gray correlation analysis