一种基于分数阶微分的FREAK改进算法
2016-12-02顾亚军胡伏原
顾亚军,胡伏原
(苏州科技大学电子与信息工程学院,江苏苏州215009)
一种基于分数阶微分的FREAK改进算法
顾亚军,胡伏原*
(苏州科技大学电子与信息工程学院,江苏苏州215009)
随着移动设备(智能手机、移动平板)技术的快速发展,移动端的特征匹配研究受到了愈来愈多的关注。该文在FREAK(Fast Retina Keypoint)算法的框架下,引入分数阶微分,改进特征表示环节,提高特征表示的准确性;在特征匹配中考虑移动设备计算能力不足的问题,引入层次化匹配策略提高特征匹配正确率。实验结果表明:改进算法提取的特征点数目比原始算法提高了近30%,匹配正确率平均提高近40%。
分数阶微分;特征表示;图模型;特征匹配
随着移动设备(智能手机、移动平板)技术的快速发展,其应用范围日趋广泛,手机地图、全景拍摄、图片美化等已成为各移动终端的常用软件。在这些应用的处理过程中,图像特征匹配都是一个关键步骤[1]。
在移动端图像特征匹配算法中,点特征因提取容易,匹配灵活[2],受到普遍关注。其基本思想是通过获取点特征周围的纹理描述,并引入距离约束计算各点相似度以实现同名点对的匹配[3-7]。长期以来,研究者希望设计具有高检测率和重复率的特征,并能够克服尺度、旋转、光照及噪声等外部情况影响。M.Calonder在2010年提出了BRIEF(Binary RobustIndependent Elementary Features)特征算法[8],该方法通过随机提取图像块(image patch)中的像素对,进行τ测试组成二进制比特串。为达到理想的描述精度,该策略产生的点对数目往往很大且忽略考虑特征方向,因此,特征在描述图像时准确性不理想。Rublee等人[9]结合了FAST(Features From Accelerated Segment Tes)和BRIEF,提出了ORB(An Efficient Alternative to SIFT or SURF)算法,在BRIEF基础上使二值描述符具备了旋转不变性,但在特征表示中,ORB忽略了图像尺度的变化。为此Stefen Leutenegger提出了二值鲁棒尺度不变点特征(Binary RobustInvariant Scalable Keypoints,BRISK)[10],该方法首先建立图像金字塔,采用FAST点检测模板提取潜在特征点。在特征点附近采用有限抽样点数目的抽样模式(pattern)组成多个点对(pair)进行τ测试,构成点特征描述子。类似地,具有代表性研究的还有Alahi等人[11]提出的FREAK算法,该算法是一种基于人眼视网膜细胞分布的抽样模式[12],越靠近关键点中心的区域采样点越密集,从而有效地提高了点描述的准确性。
上述点特征检测与表示的方法都是基于整数阶微分计算得到的特征向量,这容易受到其他信息的干扰,且会大幅度地衰减低频信息,尤其是处于平坦区域的目标特征。而分数阶微分在图像甚低频是一种非线性保留,图像在经过其处理后,平滑区域的纹理特征不但没有受到衰减,反而在一定程度上得到非线性保留。因此,文中结合分数阶微分改进了FREAK特征表示方法;同时,为了提高点匹配精度,在距离相似度的基础上引入形状约束构建结构不变图模型,通过层次化的匹配策略实现了适合于移动设备的快速匹配。
1 FREAK算法
FREAK算法在特征提取时为满足尺度不变性,首先构建图像尺度空间金字塔,并且在每一层使用FAST-9特征检测模板提取潜在特征点,公式如下

其中I(x)为半径为9的圆周上的像素点灰度,I(p)为中心点的灰度,εd为灰度差阈值,N代表满足条件的周边像素的数量。如果N大于给定的阈值(一般为圆周上像素点数量的三分之二),则可认定p为一个潜在的特征点。由于FAST算法无法区分角点和边缘点,因此,采用非极大值抑制方法对潜在特征点进行优化,提高特征点质量。
在人眼视网膜成像和识别机制的启发下,Alexandre提出在特征点周围进行区域采样,示意图如图1所示。

图1 视网膜采集模型
图1中,中心点为特征点,周围的采样圆半径随着距离中心点距离的增大而变大并伴有部分重叠。选取中心对称的取样区域,计算图像局部梯度值g(pi,pj)用于构建特征点方向,并结合τ测试获取点的二值描述子。局部梯度计算公式如下
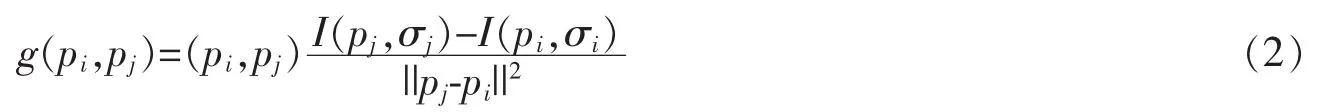
2 基于分数阶微分改进的FREAK算法
2.1 分数阶微分梯度算子
FREAK算法在特征提取时采用基于整数阶微分梯度算子的FAST检测算法,由幅频特性曲线可知,经过整数阶微分处理过后的图像在甚低频有所抑制,图像平滑区域特征点数量较少,难以准确描述图像局部信息,从而降低了图像匹配正确率。而经过分数阶微分处理过的图像平滑区域的纹理细节不但没有受到大幅度的线性衰减,反而在一定程度上实现了对纹理的非线性保留[13-16]。基于分数阶微分公式(1)变为

其中,v为分数阶微分的阶次,一般选择为0.3~0.7之间。为进一步细化公式,假设图像在X和Y轴的分数阶微分在一定条件下可分,则分数阶微分可表示为
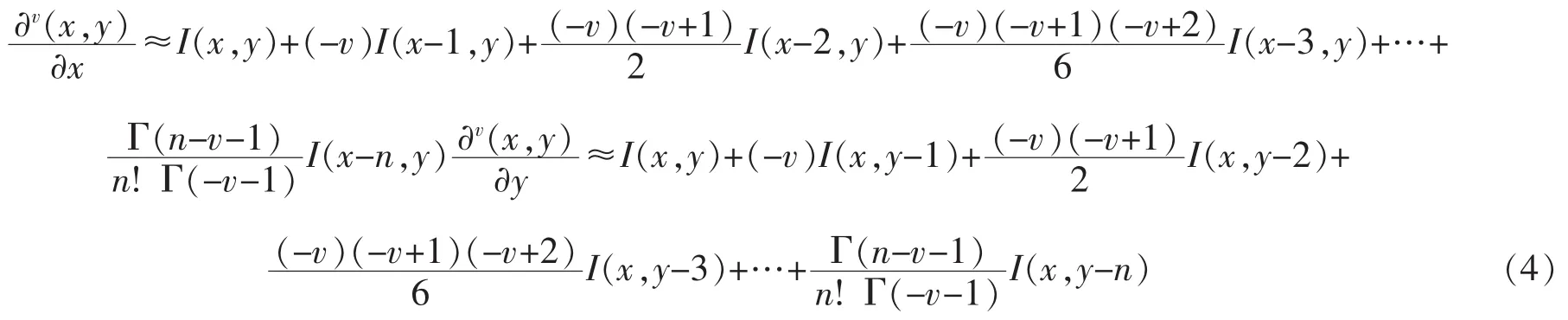
为简化计算,较少时间开销,取公式(4)前三项系数将代入式(3),则可得到基于分数阶微分的改进FAST特征检测梯度算子,公式如下
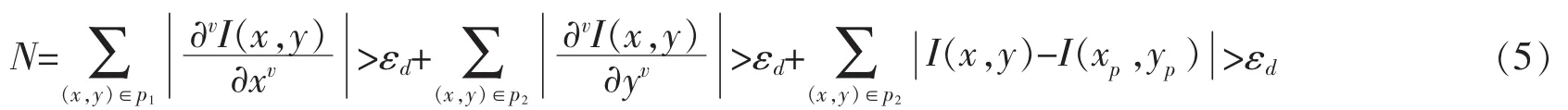
其中,p1为特征点p水平方向上左右两个点的点集,p2为特征点p垂直方向上左右两个点的点集,p3为圆周上剩余点的点集。
FREAK在特征描述时,采用对称于中心点的采样点对,根据公式(2)所示的梯度计算特征点主方向,计算简单但其也存在明显的缺点。对于图像平滑区域或者纹理复杂区域,其使用的整数阶微分难以刻画图像局部特征点,使得在上述区域内所得到的特征主方向不稳定,从而导致处于同一场景中的同一特征点的描述子之间出现误匹配。因此,考虑将分数阶微分引入梯度算子中,重新构建基于分数阶微分的图像局部梯度,公式如下
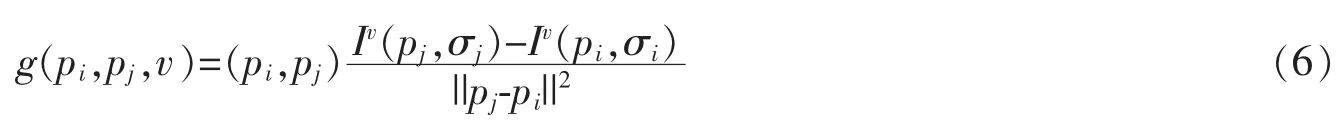
其中,Iv(p,σ)=G(x,y,σ)*w(x,y)*I(x,y)进行卷积运算,w(x,y)为点I(x,y)的微分,其模板半径大小与高斯模板相同。
2.2 基于结构保持的层次化特征匹配
FREAK算法在特征匹配时采用单一Hamming距离策略,当特征点数量较多时误匹配率较高。基于此,文中在稠密点匹配[17]的启发下,通过在引入形状约束,从距离和角度两个方面对特征点位置进行约束,以期提高特征匹配的正确率。此外,针对移动设备计算能力不足的缺点,采用层次化的匹配方法,以有效避免算法中的推理和学习过程,提高特征匹配效率。
2.2.1层次化的特征匹配
在图像特征匹配中,通常使用Hamming距离进行点特征的相似性检测,公式如下

其中,ξ为设定的阈值,其大小关系着图像特征匹配的正确率。如其值设定过小,则匹配要求过于严格,正确率也随之下降。但其也存在下限值,当低于此下限值时,特征匹配正确率保持不变。受此启发,文中通过设定ξ值来构建强匹配点对集合,即ξ值较小时的正确匹配点对。对于弱匹配点对,即未能成功匹配的点对,通过周围强匹配对进行结构辅助匹配。为降低算法时间复杂度,在强匹配点对随机选取两对,构建结构保持的层次化匹配模型进行搜索匹配。
(1)强匹配点对集构建:利用公式(7),通过设定较小的ξ值来获得匹配度大的关键点对Vm,公式如下


表1 图约束层次化匹配方法实现步骤
(2)弱匹配点对匹配:对图像中未构成匹配的特征点对进行匹配,考虑特征点之间结构相似性和距离约束,构建结构保持的图模型

式中,φ为特征点对之间的相似度;(α,β)为两幅图像中的特征点点集;χm=(xm,ym)为点m的位置。在特征点匹配时,s值越大,说明匹配度越高。
2.2.2结构保持的图匹配
通常情况下,可以通过推理与学习的方法求解公式(9)。但考虑到移动设备对图模型的推理和计算能力不足,因此,文中采取随机在Vm中取两对强匹配点,并引入角度变化简化图模型
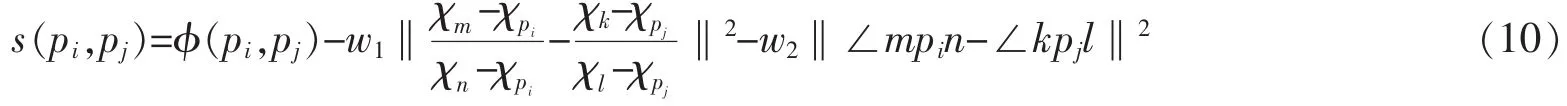
式中,w1,w2为权重系数,代表了距离和角度对结果s的贡献度,一般情况下设为相同的值。适于移动应用的匹配示意图如图2所示。
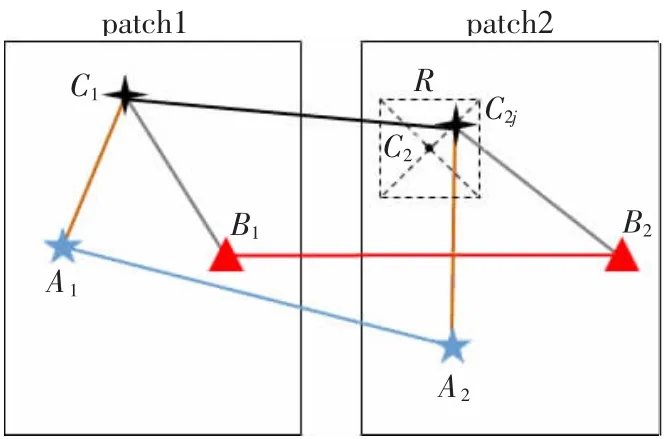
图2 适于移动应用的特征匹配示意图
图中{A1,A2},{B1,B2}为Vm中随机选取的两对强匹配点。为快速预测待匹配点的位置,利用三角形的△A1B1C1~△A2B2C2和下式,在图像patch2中寻找patch1中点C1的匹配点可能存在的区域R。然后通过公式(10),在R区域中寻找到s值最大的点即为匹配点。算法实现步骤见如表1。
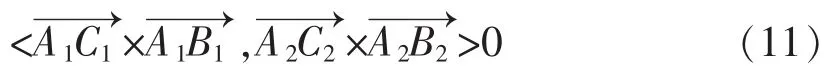
3 实验结果分析
为验证文中算法的有效性,将改进算法与原始算法分别基于iPhone6进行特征表示和特征匹配对比实
验。实验中选取Mikolajczyk和Schmid所使用的Graffiti库[18]作为标准测试库,通过模拟现实环境中存在的各种干扰因素(模糊、光照、旋转及尺度变换)充分验证文中算法的鲁棒性。
3.1 特征点提取实验对比
将特征点提取实验分为四组,分别对应上述四种不同的图像变换,并且在每组中选择两幅图片对改进算法与原始算法在特征点数量上进行比较。实验结果如图3所示,详细实验数据见表2。从实验结果图可以看出,改进算法相比原始算法在图像平滑区域提取的特征点数量明显增多。且从表2中实验数据可以看出,图像整体特征检测数量也有明显上升,平均新增率达到30%左右。

图3 图像特征点提取比较

表2 特征提取实验详细数据对比
3.2 特征点匹配
为验证文中算法的有效性,将分别从特征匹配成功率、正确匹配新增率两个方面对改进算法、原始算法、ORB算法及BRISK算法进行全面分析对比,实验结果如图4所示,详细实验数据见表3。

图4 特征匹配对比

表3 特征匹配实验详细数据对比
从实验结果图和数据对比中可以看出,经过改进匹配方法的匹配正确率都较高,且相比原始算法匹配正确率有大幅提高(方向一致的正确匹配线密集,错误匹配线稀疏)。其中,在旋转变化中,由于两幅图像旋转角度偏大(60°),因此,匹配结果略低,但与其他结果相比,仍然具有很好的鲁棒性。
4 结语
近年来,移动端图像特征匹配受到越来越多的关注,但由于移动端的特殊性,特征匹配的结果不甚满意。为此,文中提出了一种适于移动应用的改进FREAK算法,着重对特征表示和匹配中的两个关键步骤进行改进。通过实验表明,经过改进的FREAK算法在特征提取数量以及匹配正确率方面都有较大提高。
[1]张丽敏.基于分数阶微积分的图像特征匹配的方法研究[D].重庆:重庆大学,2011.
[2]贾棋,高新凯,罗钟铉.基于几何约束的特征点匹配方法[J].计算机辅助设计与图形学学报,2015,27(8):1388-1397.
[3]李映,崔杨杨,韩晓宇.基于线特征和控制点的可见光SAR图像配准[J].自动化学报,2012,38(12):1968-1964.
[4]LOWE D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[5]KE Y,SUKTHANKAR R.PCA-SIFT:a more distinctive representation for local image descriptors[C]//Proceedings ofIEEE Computer Society Conference on Computer Vision and Pattern Recognition.IEEE,2004:506-513.
[6]BAY H,TUYTELAARS T,GOOL L V.SURF:speed up robust features[C]//Proceedings of the European Conference on Computer Vision.IEEE,2006:404-417.
[7]ENGIN T,VINCENT L,PASCAL F.DAISY:an efficient dense descriptor applied to width-baseline stereo[J].IEEE Transactions on Pattern Analysis MachineIntelligence,2010,32(5):815-830.
[8]CALONDER M,LEPETIT V,STRECHA C,et al.BRIEF:binary robust independent elementary features[C]//Proceedings of the 11th European conference on Computer vision:PartIV.Springer-Verlag,2010:778-792.
[9]RUBLEE E,RABAUD V,KONOLIGE K,et al.ORB:An efficient alternative to SIFT or SURF[J].Proceedings,2011,58(11):2564-2571.
[10]LEUTENEGGER S,CHLIM,SIEGWART R Y.BRISK:Binary Robust invariant scalable keypoints[C]//Computer Vision(ICCV),2011IEEEInternational Conference on.IEEE,2011:2548-2555.
[11]ORTIZ R.FREAK:Fast Retina Keypoint[C]//IEEE Conference on Computer Vision and Pattern Recognition.IEEE,2012:510-517.
[12]OLSHAUSEN B A,FIELD D J.What is the other 85%of V1 doing?[C]//23 Problems in Systems Neuroscience,2004.
[13]姒绍辉,胡伏原,付保川,等.自适应非整数步长的分数阶微分掩模的图像纹理增强算法[J].计算机辅助设计与图形学学报,2014,26(9):1438-1449.
[14]周激流,蒲亦非,廖科.分数阶微积分原理及其在现代信号分析与处理中的应用[M].北京:科学出版社,2010.
[15]HU F,SIS,WONG H S,et al.An adaptive approach for texture enhancement based on a fractional differential operator with non-integer step and order[J].Neurocomputing,2014,158:295-306.
[16]胡伏原,姒绍辉,张艳宁,等.自适应分数阶微分的复合双边滤波算法[J].中国图象图形学报,2013,18(10):1237-1246.
[17]ZHANG L,MAATEN L J P V D.Preserving structure in model-free tracking[J].IEEE Transactions on Pattern Analysis&MachineIntelligence,2014,36(4):756-769.
[18]MIKOLAJCZYK K,TUYTELAARS T,SCHMID C,et al.A comparison of affine region detectors[J].International Journal of Computer Vision,2005,65(1/2):43-72.
An improved FREAK algorithm based on fractional differential
GU Yajun,HU Fuyuan
(School of Electronic&Information Engineering,SUST,Suzhou 215009,China)
With the rapid technology development of mobile devices(smart phones,mobile tablet),the research on the characteristics of mobile terminals has received increasing attention.Based on the FREAK(Fast Retina Keypoint)algorithm,we introduced fractional differential to improve the feature representation accuracy.Taking the deficiency of computing capability of mobile devices into consideration,we introduced the concept of hierarchical matching strategy to improve the feature matching accuracy.The experimental results show that the improved algorithm can improve the number of feature points by nearly 30%and the matching accuracy by 40%against the original algorithm.
fractional differential;feature representation;graph model;feature matching
O175;TP391
A
1672-0687(2016)04-0062-06
责任编辑:艾淑艳
2016-04-05
国家自然科学基金资助项目(61472267)
顾亚军(1990-),男,江苏泰州人,硕士研究生,研究方向:移动端特征匹配。
*通信联系人:胡伏原(1978-),男,教授,博士,硕士生导师,E-mail:fuyuanhu@mail.usts.edu.cn。
