基于复频率衰减反传算子的全波形反演梯度构建

梁展源 吴国忱

(中国山东青岛266580中国石油大学(华东)地球科学与技术学院)



基于复频率衰减反传算子的全波形反演梯度构建

梁展源吴国忱

(中国山东青岛266580中国石油大学(华东)地球科学与技术学院)

从梯度构建中反传算子的角度出发， 本文分析了影响梯度精度的因素， 并提出了一种新的基于复频率衰减反传算子的全波形反演梯度构建法， 以压制梯度构建过程中产生的弧状噪音； 针对全波形反演的巨大存储量和精度问题， 本文采用限内存的BFGS(L-BFGS)算法进行迭代反演． 对平层模型、 逆掩断层模型以及凹陷模型的测试结果表明， 与常规梯度算法相比， 基于复频率衰减反传算子算法所构建梯度的精度得到明显改善． 用复杂断块模型进行全波形反演测试， 并将其与常规算法得到的反演速度精度进行对比， 结果验证了该方法的正确性及其对提高梯度精度的有效性．

全波形反演 梯度算子 复频率衰减 L-BFGS

引言

随着世界油气资源的日益紧张， 勘探难度也日益增大， 对地震成像精度的要求也越来越高， 因此发展高精度地震勘探技术迫在眉睫． 全波形反演法利用叠前地震资料的运动学和动力学信息重建地层结构， 揭示复杂地质背景下的构造和储层物性， 已成为当今地球物理学界的热点技术． 自1984年以来， 全波形反演法大致经历了3个发展阶段： ① 20世纪80—90年代为该方法理论框架建立阶段(Lailly， 1983； Tarantola， 1984)； ② 20世纪90年代—21世纪初为该方法的稳定发展阶段(Li， Demmel， 2003; Sirgue， Pratt， 2004; Shin， Cha， 2009; Virieux， Operto， 2009)， 主要代表为Pratt(1999)的频率域全波形反演法； ③ 2005年至今为该方法蓬勃发展阶段， 其在反演频率选择策略、 目标函数设置方式、 震源子波处理方式、 梯度预处理方法、 初始模型建立和效率优化等方面取得了重要进展(Plessix， 2006； Ben-Hadj-Alietal， 2011; Warneretal， 2013)． 目前全波形反演已逐步从二维发展到三维， 从声波发展到弹性波， 从单参数发展到多参数， 从理论模型验证发展到实际资料反演．

在时间域全波形反演中， Lailly(1983)和Tarantola(1984)等提出基于最小二乘理论的广义非线性反演法， 即通过利用剩余波场的反向传播与正向波场的互相关来计算反演问题中目标函数的负梯度方向， 以实现波形反演过程． 梯度算子构建与基于互相关成像条件的逆时偏移类似， 均需进行正传波场与反传波场的互相关计算， 因此在全波形反演梯度算子构建的过程中， 会产生一系列与逆时偏移类似的噪音． 针对低频噪音问题， Youn和Zhou(2004)提出了利用拉普拉斯滤波去除低频噪音的方法； Suh和Cai(2009)提出将波场分为上行波和下行波， 在频率-波数域进行低频噪音的压制； 郭念民等(2013)对拉普拉斯滤波进行改进， 采用高阶拉普拉斯滤波取得了很好的噪音压制效果． 杨午阳等(2013)对全波形反演存在的反演非唯一性、 噪声敏感性等问题进行调研， 介绍了地震全波形反演法在时间域、 频率域和拉普拉斯域内的改进和优化策略． 与逆时偏移不同的是， 全波形反演是对模拟数据与观测数据的残差进行反传， 而逆时偏移是对观测数据进行反传， 因此影响梯度算子精度的因素更多， 如子波的选取、 初始模型的构建以及覆盖次数的匹配等， 而且还需要模拟数据与观测数据更好地匹配．

复频率的主要作用是对波场进行衰减， 去除周期混叠现象及减少数据孔径等． 在全波形反演算法中， 曹书红和陈景波(2014)利用复频率的衰减特性对整个子波进行衰减， 从而构建更加精确的初始速度． 与常规复频率的算法不同， 本文拟结合完全匹配层在复频率域衰减的算法， 在求取全波形反演梯度过程中， 通过改进残差反传算子， 仅在边界处进行噪音衰减， 减少梯度噪音， 以获取更高精度的梯度．

鉴于此， 本文首先从理论推导上引入复频率衰减反传算子来压制噪音的产生； 然后用不同的速度模型进行测试， 对比复频率衰减反传算法与常规算法所构建的梯度精度； 最后基于限内存的拟牛顿(limited memory BFGS， 简写为L-BFGS)算法进行复杂断块模型的反演速度测试， 以验证本文算法对梯度精度的改进以及提高速度场分辨率的有效性和可行性．

1 全波形反演基本原理

1.1 目标函数

全波形反演大致分为3个步骤： 目标函数的建立、 梯度的求取和迭代反演． 目标函数可直接影响全波形反演的非线性强度， 本文采用Tarantola(1984)提出的最小二乘目标函数． 首先利用实际野外观测的地震记录uobs与正演得到的观测记录ucal进行匹配， 求取波场的数据残差δd， 即

(1)

然后构建最小二乘目标函数， 使误差函数E(v)最小， 即

(2)

式中，m为变量参数，RN为N维参数空间．

1.2 梯度算子

梯度算子的构建是全波形反演中至关重要的一步， 其精度将直接影响反演的速度． Tarantola(1984)在建立全波形反演理论框架的同时， 利用源波场与残差波场进行互相关计算求取梯度算子， 避免了直接求取雅可比(Jacobi)矩阵. 之后Plessix(2006)又重新推导了基于伴随状态法的时间域全波形梯度算子公式， 即

(3)

式中，g为目标函数的梯度矩阵, E为野外记录与正演模拟记录的残差，v为介质速度， J为雅克比矩阵，xs为震源数，u(t)为震源的正传波场，q(T-t)为以波场数据残差为震源进行波场逆时反传的波场记录，T为最大时间．

1.3 L-BFGS算法

全波形反演具有强烈的非线性， 通常采用局部线性化的方法求解非线性问题． 在最优化理论中， 常用的方法有最速下降法、 共轭梯度法和拟牛顿法(BFGS)等． 考虑到拟牛顿法的精度更高， 收敛速度更快， 因此本文采用拟牛顿法进行迭代． 但拟牛顿法需要求取海森(Hessian)矩阵， 需要大量的存储空间， 因此为避免该问题， 诸多研究者对BFGS算法进行了改进， 例如： Perry(1977)和Shanno(1978)最先提出了有限内存的共轭梯度算法； Nocedal(1980)在BFGS算法的基础上， 提出了L-BFGS算法． 本文在全波形反演迭代更新速度时， 采用的便是L-BFGS算法．

2 基于复频率衰减反传算子的梯度算子构建

将二维标量波方程在时间域作傅里叶变换， 得到频率域的二维标量波方程为

(4)

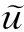
(5)

式中，sx为空间坐标与复数坐标之间的变换算子，σx为x方向的衰减算子． 将式(5)带入式(4)可导出：

(6)

将式(6)变换至频率域， 得到x方向频率域的衰减表达式为

(7)

将式(7)重新改写， 得到复频率衰减记录为

(8)

式中，R为z=0处的波场值，F-1为傅里叶逆变换．

在常规全波形反演中, 模拟数据记录可表示为

(9)

对比式(8)与式(9)可以看出， 式(9)为常规反传时所需的震源， 其σx=0， 不含有衰减项； 而式(8)中含有复频率衰减因子σx， 在残差反传过程中， 能将边界吸收的波场同时反传， 以达到衰减弧状噪音的目的．

根据式(8)对实际观测数据d作相似衰减处理后记为dc， 得到目标函数：

(10)

根据伴随状态法得到基于复频率衰减反传算子的梯度表达式为

(11)

式中，L*[dc-(Ru)c]为将含有复频率衰减因子的观测记录与模拟数据的残差反传到整个模型空间． 可以看出， 式(11)与式(2)形式一样， 但其残差内核引入了复频率衰减反传算子．

图1 常规全波形反演流程图虚线框内为复频率衰减反传算子 Fig.1 The flow chart of conventional full waveform inversion The complex frequency attenuation back propagation operator is represented by the dashed rectangle

3 模型测试

图1为常规全波形反演流程图． 可以看出， 全波形反演算法环环相扣， 其核心是梯度算子的构建． 为了得到最终高分辨率的速度参数， 需保证正演波场、 反传算子和目标函数梯度的精度. 求取全局梯度后， 再求取一个合适的步长即可对速度参数进行更新． 本文在计算波场残差时引入了复频率衰减算子项， 改变了波场残差的逆时传播， 以达到去除噪音的效果．

下文将介绍模型测试． 以下测试中， 正演波场与残差反传模拟均用了时间2阶、 空间10阶的有限差分算法， 参数的选择均满足稳定性条件和频散关系． 考虑到全波形反演的反演精度和大存储量问题， 本文采用L-BFGS与线性搜索相结合的方法进行迭代更新．

3.1 平层模型测试

首先以一个简单的平层各向同性均匀模型(图2)为例测试复频率衰减效果. 平层模型网格大小为400×400， 网格间距为dx=dz=5 m， 时间采样间隔为dt=0.6 ms， 时间点数为nt=2200． 图2a为真实模型， 上、 下两层速度分别为3 km/s和4 km/s； 图2b为初始平滑模型．

图2 平层的真实模型(a)和初始平滑模型(b)

图3 平层模型观测记录与模拟记录的残差 Fig.3 The residuals between obser-vation records and simulation ones of the single layer model

图3为上述平层真实模型正演得到的观测记录与初始平滑模型正演得到的模拟记录的残差． 可以看出， 由于人工边界的作用， 导致同相轴在边界处被截断， 截断点产生绕射， 从而产生弧状噪音， 如图4所示． 可以看出， 与常规算法相比， 利用复频率衰减反传算子所得到的有效成像波场更加突出， 即弧状干扰噪音(黄色箭头)更弱． 由于全波形反演梯度构建的核心在于正传波场与反传波场的互相关， 因此这种弧状噪音必定会引入到梯度中， 从而影响梯度的精度． 用上述平层模型进行等间距放10炮测试， 炮点位于地表处．

图5为由常规算法和复频率衰减反传算子算法所构建的梯度， 炮数为10， 分布在模型上表层． 可以看出， 弧状噪音严重影响梯度算子的精度， 相同的炮数， 用复频率衰减反传算子求取的梯度中， 反射界面以上的弧状噪音明显减弱． 由于弧状噪音是由边界处截断的绕射所产生， 所以多炮叠加可以压制这种噪音． 常规算法都是采用更多的炮数来压制这种绕射噪音， 但在观测系统变化比较剧烈的地区， 可能存在炮数不足的情况， 这时弧状噪音就得不到很好的压制， 则会影响梯度的精度， 从而影响反演速度， 而利用复频率衰减反传算子则可以很好地压制这种弧状噪音． 下面将以几种更加复杂的模型测试说明基于复频率衰减反传算子的全波形反演梯度构建算法的可行性和有效性．

图4 由常规算法(a)和复频率衰减算子算法(b)所构建的残差反传波场红线为界面所在位置， 黄色箭头为噪音， 下同

图5 由常规算法(a)和复频率衰减反传算子算法(b)所构建的梯度

3.2 逆掩断层模型测试

设计一个逆掩断层模型对梯度精度进行测试． 该模型网格大小为400×400， 网格间距为dx=dz=5 m， 时间采样间隔为dt=0.6 ms， 时间采样点数为nt=2200， 震源主频为20 Hz． 逆掩断层模型从上至下各层速度分别为2.5， 3.0， 3.5和4.0 km/s．

图6中的初始模型是将真实模型在x方向和z方向分别进行平滑得到的． 在逆掩断层模型测试中， 为着重对比逆掩断层处的梯度精度， 本文将最上层稍作处理， 将基于复频率衰减反传算子算法(右边)与常规算法(左边)所构建的梯度均绘制于图7中进行对比． 可以看出， 右边图的弧状噪音明显减弱(图中黄色箭头)， 且有效同相轴更加连续清晰．

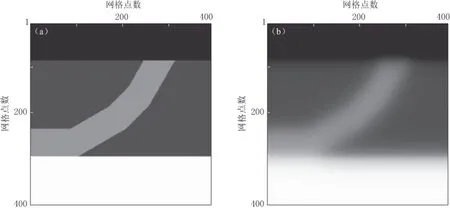
图6 逆掩断层的真实模型(a)和初始模型(b)

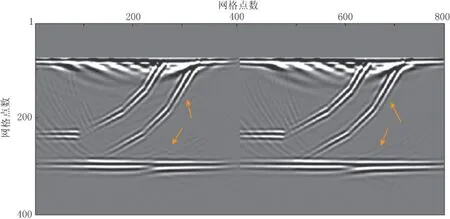
图7 由常规算法(左)与复频率衰减反传算子算法(右)所构建的梯度对比

3.3 不同炮数的影响

在全波形反演过程中， 影响梯度成像结果的因素很多， 如子波、 初始速度模型和覆盖次数(不同炮数)等． 针对梯度构建过程中所产生的弧状噪音， 通常利用更多的炮数压制这种绕射干扰． 下面利用不同炮数进行测试， 对比不同炮数对成像精度的影响， 同时也对本文提出的基于复频率衰减反传算子所构建的梯度与常规算法所构建的梯度进行对比， 并予以分析．

设计一个凹陷模型， 网格大小为400×400， 模型从上至下各层速度分别为2.5， 3.0， 3.5和4.0 km/s． 网格间距为dx=dz=5 m， 时间采样间隔为dt=0.6 ms， 时间采样点数为nt=2200， 震源主频为30 Hz. 下面分别进行5炮、 10炮和20炮测试．

图8为真实凹陷模型和凹陷初始模型． 图9展示的是不同炮数对构建梯度的影响. 可以看出， 炮数越多, 弧状噪音越少， 成像效果越好． 对于400×400网格点的凹陷模型， 在5炮测试时弧状噪音干扰严重， 对梯度的信噪比影响较大； 在10炮测试时， 弧状噪音也较为明显， 但较5炮明显减弱； 在20炮测试时， 同相轴更加连续， 几乎看不出弧状噪音. 随着炮数的增加， 弧状噪音依次减弱， 同相轴连续性更好， 成像效果也更好． 对比图9a--c的成像精度可以看出， 图9a(下)成像效果改善最明显， 图9b(下)其次， 而图9c(上)与图9c(下)几乎一致， 说明基于复频率衰减反传算子在炮数越少的时候对梯度精度改善效果越明显， 炮数越多， 则与常规算法改善效果相当． 因此对实际情况中炮数或者覆盖次数不够多的地方以及观测系统变化较为剧烈的地带， 基于复频率衰减反传算子算法所求取的梯度精度更高．

图8 真实凹陷模型(a)和凹陷初始模型(b)

图9 5炮(a)、 10炮(b)和20炮(c)测试时由常规算法(上)与复频率 衰减反传算子算法(下)所构建的梯度对比

3.4 复杂断块模型测试

3.4.1 方法有效性检验

采用如图10所示的复杂断块模型进行全波形反演测试， 将复杂断块模型进行平滑得到初始速度场， 该速度场包含全波形反演所需的低波数成分． 反演中深度方向采样间隔为2 m， 测线方向采样间隔为5 m， 子波主频为60 Hz．

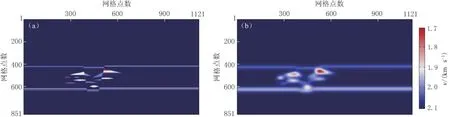
图10 复杂断块的真实模型 (a)和初始模型(b)

在反演过程中， 首先进行梯度的构建， 再对梯度作预处理(Pratt， 1990)， 以解决由于震源位置包含奇点和模型中照明能量分布不均匀的问题， 即利用L-BFGS算法构建伪海森矩阵对梯度进行约束， 对误差函数采用2阶寻优法， 这样既保证了收敛速度和反演精度， 又不耗费存储量． 图11为复杂断块模型测试中由常规算法与复频率衰减反传算子算法所构建的梯度对比， 两者均对梯度进行了预处理． 可以看出， 进行梯度预处理后浅层和深层能量分布均匀， 且基于复频率衰减反传算子算法所构建的梯度对弧状噪音的压制效果更好， 所得梯度的同相轴更加连续， 受到噪音干扰更少．

图11 由常规算法(a)与复频率衰减反传算子算法(b)所构建的梯度对比红色虚线框为红色实线框放大后的结果

图12为基于复频率衰减反传算子算法反演得到的复杂断块模型速度场． 可以看出， 梯度中所产生的弧状噪音基本被压制， 速度精度明显得到提高， 且深、 浅层能量均衡． 从左边红色虚线框中可以看出， 边界处的弧状噪音也得到很好压制．

3.4.2 误差(精度)对比

为验证基于复频率衰减反传算子的全波形反演的收敛性， 对每次迭代的误差以及迭代多次后的速度场进行分析． 分别利用常规的全波形反演算法和本文提出的复频率衰减反传算子算法进行51次迭代， 得到最终的速度场如图13所示． 可以看出， 基于复频率衰减反传算子的全波形反演得到的速度场对速度异常体周围的噪音压制效果更好．

图12 基于复频率衰减反传算子算法反演得到的复杂断块模型速度场

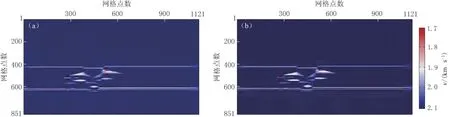
图13 由常规算法(a)与复频率衰减反传算子算法(b)得到的第51次迭代速度场对比

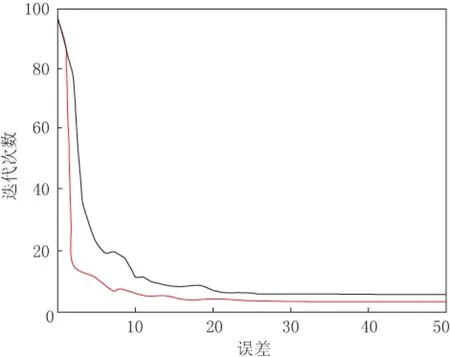
图14 由常规算法(黑色)与复频率衰减反传算子算法(红色)得到的误差下降曲线对比Fig.14 Comparison of error drop curve obtained by conventional method (black) with that by complex frequency attenuation back propagation operator method

图14为常规算法与复频率衰减反传算子算法的收敛过程对比． 可以看出， 两种算法均可以收敛至稳定值， 但基于复频率衰减反传算子的全波形反演算法的误差下降速率明显快于常规算法， 且最后的收敛值更低， 说明改进后的算法每次求得的梯度更精确， 所得的最终速度场精度更高．

3.4.3 对初始模型的依赖性

全波形反演是高度非线性的， 对初始速度模型依赖性较强， 如果初始速度严重偏离真实速度， 则反演很难收敛至全局极小值， 易陷入局部极小． 全波形反演首先需要理想的初始速度作为输入速度， 然而从实际地震数据中很难得到如图10b所示的初始速度， 因此， 需要测试基于复频率衰减反传算子的全波形反演算法对初始模型的依赖性．

图15a为平滑程度较低的初始速度模型， 其低波数速度信息充足， 位置准确， 偏离真实速度较少； 图15b为平滑程度较高的初始速度模型， 其严重偏离了真实速度模型． 分别将这两个速度模型作为初始速度模型， 用本文的改进算法进行全波形反演测试， 迭代51次后所得到的速度场如图16所示． 从图中黄色圆圈所示位置可以看出， 同样迭代51次， 当初始速度模型偏离真实速度模型较大时， 其反演速度的准确度降低， 并且由于走时的影响， 下层界面的位置归位不准确， 出现弯曲现象， 可见全波形反演对初始模型的依赖性较强．

图15 平滑程度较低(a)和平滑程度较高(b)的初始速度模型

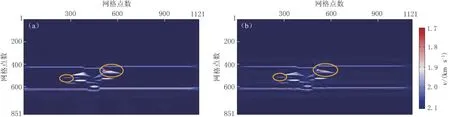
图16 图15a(a)和图15b(b)的初始速度模型所对应的第51次迭代的速度场

4 讨论与结论

本文在全波形反演梯度构建过程中， 分析了影响梯度精度的因素， 提出了基于复频率衰减反传算子的梯度构建法， 采用限内存的BFGS(L-BFGS)算法进行迭代反演， 并用不同的速度模型进行测试， 得到如下结论：

1) 理论与数值试例均表明， 采用复频率衰减反传算子所构建的梯度能更好地压制弧状噪音， 反演过程中误差值收敛得更快， 反演结果精度更高．

2) 全波形反演的一大难点是巨大的存储量和计算量问题， 而复频率衰减反传算子算法在提高梯度精度的同时， 几乎不增加计算量和存储量．

3) 本文方法可以扩展到实际资料的应用中， 在观测系统变化比较剧烈、 炮数缺失及覆盖次数不足的情况下， 复频率衰减反传算子算法可以提高全波形反演的精度．

本文尚未对实际资料进行测试， 对实际资料中压制弧状噪音的应用还有待进一步的研究．

曹书红， 陈景波. 2014. 频率域全波形反演中关于复频率的研究[J]. 地球物理学报， 57(7): 2302--2313.

Cao S H， Chen J B. 2014. Studies on complex frequencies in frequency domain full waveform inversion[J].ChineseJournalofGeophysics， 57(7): 2302--2313 (in Chinese).

郭念民， 冯雪梅， 李海山. 2013. 高阶拉普拉斯算子逆时偏移低频噪声去除方法[J]. 石油物探， 52(6): 642--649.

Guo N M， Feng X M， Li H S. 2013. Research on higher-order Laplace operator denoising method in reverse-time migration[J].GeophysicalProspectingforPetroleum， 52(6): 642--649 (in Chinese).

杨午阳， 王西文， 雍学善， 陈启燕. 2013. 地震全波形反演方法研究综述[J]. 地球物理学进展， 28(2): 766--776.

Yang W Y， Wang X W， Yong X S， Chen Q Y. 2013. The review of seismic full waveform inversion method[J].ProgressinGeophysics， 28(2): 766--776 (in Chinese).

Ben-Hadj-Ali H， Operto S， Virieux J. 2011. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J].Geophysics， 76(4): R109--R124.

Lailly P. 1983. The seismic inverse problem as a sequence of before stack migrations[C]∥ConferenceonInverseScattering：TheoryandApplication. Philadelphia: Society for Industrial and Applied Mathematics： 206--220.

Li X S， Demmel J W. 2003. SuperLU_DIST: A scalable distributed-memory sparse direct solver for unsymmetric linear systems[J].ACMTransMathSoftw， 29(2): 110--140.

Nocedal J. 1980. Updating quasi-Newton matrices with limited storage[J].MathComp， 35(151): 773--782.

Perry J M. 1977.AClassofConjugateGradientAlgorithmsWithaTwo-StepVariableMetricMemory[M]. Evanston, Illiois: Northwestern University Press: 53--55.

Plessix R. 2006. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J].GeophysJInt， 167(2): 495--503.

Pratt R G. 1990. Inverse theory applied to multi-source cross-hole tomography， part 2: Elastic wave-equation method[J].GeophysProsp， 38(3): 311--329.

Pratt R G. 1999. Seismic waveform inversion in the frequency domain， part 1: Theory and verification in a physical scale model[J].Geophysics， 64(3): 888--901.

Shanno D F. 1978. On the convergence of a new conjugate gradient algorithm[J].SIAMJNumerAnal， 15(6): 1247--1257.

Shin C， Cha Y H. 2009. Waveform inversion in the Laplace-Fourier domain[J].GeophysJInt， 177(3): 1067--1079.

Sirgue L， Pratt R G. 2004. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies[J].Geophysics， 69(1): 231--248.

Suh S Y， Cai J. 2009. Reverse-time migration by fan filtering plus wavefield decomposition[C]∥ExpandedAbstractsof74thAnnualInternationalSEGMeeting. Houston， Texas: Society of Exploration Geophysicists: 2804--2808.

Tarantola A. 1984. Inversion of seismic reflection data in the acoustic approximation[J].Geophysics， 49(8): 1259--1266.

Virieux J， Operto S E P. 2009. An overview of full-waveform inversion in exploration geophysics[J].Geophysics， 74(6): WCC1--WCC26.

Warner M， Ratcliffe A， Nangoo T， Morgan J， Umpleby A， Shah N， Vinje V， Stekl I， Guasch L， Win C， Conroy G， Bertrand A. 2013. Anisotropic 3D full-waveform inversion[J].Geophysics， 78(2): R59--R80.

Youn O K， Zhou H W. 2004. Depth imaging with multiples[C]∥ExpandedAbstractsof74thAnnualInternationalSEGMeeting. Houston， Texas: Society of Exploration Geophysicists: 1057--1061.

Full waveform inversion gradient construction based on the complex frequency attenuation back propagation operator

Liang ZhanyuanWu Guochen

(SchoolofGeosciences，ChinaUniversityofPetroleum，ShandongQingdao266580，China)

This paper analyzed the factors affecting the gradient accuracy from the view of back propagation operator， and proposed a new method for gradient construction of full waveform inversion based on complex frequency attenuation back propagation operator. The gradient construction noise can be suppressed with the proposed method. During the inversion， the BFGS (L-BFGS) method is adopted to balance the relation between the huge storage capacity and the accuracy. The tests based on single layer model, overthrust fault model and sag model validate that the proposed method can suppress the noise in the gradient construction comparing with the conventional gradient method. Then the full waveform inversion is tested on a complex faulted blocks model， and the inversion accuracy is compared with that of the conventional method， proving that the proposed method in this paper is correct and effective in improving the gradient accuracy.

full waveform inversion; gradient operator; complex frequency attenuation; L-BFGS

国家973项目(2013CB228604)资助.

2015-07-01收到初稿， 2015-09-13决定采用修改稿.

e-mail: lzy09017216@163.com

10.11939/jass.2016.02.008

P315.3+1

A