基于MPF的无模式跳跃光电振荡器
2016-12-02蒋琛彦姜源源邹卫文李曙光陈建平
蒋琛彦,姜源源,邹卫文,张 昊,李曙光,陈建平
(1.上海交通大学 区域光纤通信网与新型光通信系统国家重点实验室,上海200240;2.上海航天电子通讯设备研究所,上海201109)
基于MPF的无模式跳跃光电振荡器
蒋琛彦1,姜源源2,邹卫文1,张 昊1,李曙光2,陈建平1
(1.上海交通大学 区域光纤通信网与新型光通信系统国家重点实验室,上海200240;2.上海航天电子通讯设备研究所,上海201109)
提出一种基于微波光子滤波器的无模式跳跃的光电振荡器。理论分析并实验验证了啁啾光纤布喇格光栅与一个光纤环级联后对跳模效应的消除作用,描述了光电振荡器的相位噪声特性和色散介质的三阶色散的影响。
光电振荡器;微波光子滤波器;啁啾光纤布喇格光栅;跳模效应
0 引言
光电振荡器(OEO)能产生相位噪声较低的微波信号[1],被广泛应用于无线通信、雷达和信号处理等领域[2]。经典的OEO利用一个电带通滤波器(BPF)来选择振荡频率[3],由于BPF的有限可调性,OEO的频率调节范围有限。利用微波光子滤波器(MPF)的OEO可实现振荡频率的可调性[4]。在此类OEO中,通常采用一段较长的光纤构造高Q值的MPF[5]即可获得较低的相位噪声。MPF的中心频率会随很多因素的变化而变化,如由外部环境变化引起的折射率变化和光纤长度变化等,导致OEO的振荡频率会在MPF通带中的几个相邻振荡模式间跳跃,即跳模效应。跳摸效应不仅会造成OEO产生的微波信号频率不稳定,而且还会恶化相位噪声。为抑制该效应,研究者们提出了多环OEO、采用带宽较窄的BPF等[6]方案,但结果都不理想,跳模现象无法完全消除。文献[7]提出了一种基于相互注入锁定双波长单纵模激光器的OEO,可消除跳模效应,但这种方法需要增加很多器件,使系统结构较为复杂。文献[8]提出利用线性啁啾光纤布喇格光栅(CFBG)来构造MPF的OEO。本文在总结前人研究成果的基础上[4],采用CFBG和无限冲击响应(IIR)光纤环来消除跳模效应,提出一种基于MPF的无模式跳跃OEO。
1 OEO的基本原理
1.1 OEO的结构介绍
本文提出的OEO的基本结构如图1所示。放大自发辐射(ASE)源和可调光滤波器(TOF)作为宽带光源(BOS)产生的光经过一个3dB光耦合器(OC1)后被分成两部分,分别经过两个偏振控制器(PC)优化偏振状态后,上部分被送入可调光延迟线(VODL),下部分利用马赫-曾德尔调制器(MZM)进行调制,使整个系统的光功率最大化。利用另一个3dB光耦合器(OC2)将两部分光合并,从而形成一个内联式的马赫-曾德尔干涉仪(MZI)[4]。环形器将OC2的输出光送入CFBG后,光信号通过一个由光耦合器(OC3)构成的IIR滤波器,利用掺铒光纤放大器(EDFA)放大光信号,并通过光电探测器(PD)将光信号转换为电信号。OEO中的MZI结构和CFBG共同构成一个单边带有限冲击响应(FIR)MPF,以选择出所需OEO微波信号的频率。另外,电放大器(EA)用来增大OEO的开环增益,从而满足OEO的振荡条件,即开环增益大于1。
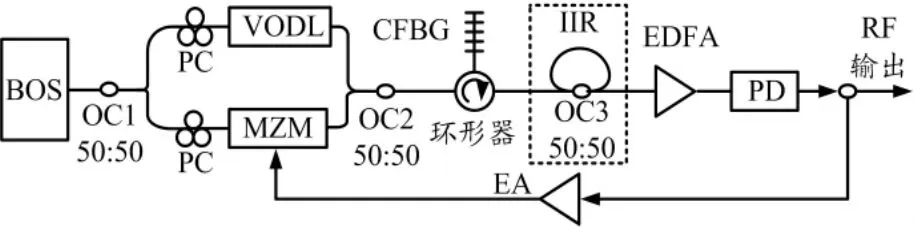
图1 OEO基本结构图
PD输出端的信号由MZI结构中的载波和边带拍频产生。若MZM的偏置电压为载波抑制点,MPF的基带响应将会消失。根据文献[5]中对MPF的分析,考虑到高阶色散,MPF的响应可表示为:
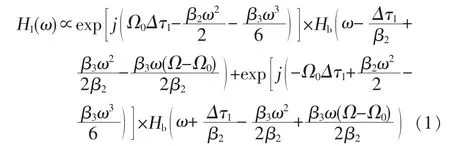
其中,Hb(ω)是MPF的基带响应,β2是CFBG的群速度色散 (GVD),β3是CFBG的三阶色散 (TOD),Δτ1是MZI结构两臂的时间延迟差,(Ω-Ω0)是相对于BOS中心频率的频偏。单边带MPF的中心频率为Δτ1/2πβ2。
OEO的模式选择由MPF决定,设τ1为OEO环的总延时,n为有效折射率,L1为OEO环的总长度,则其振荡模式的间距为1/τ1,即c /nL1。FIR MPF的典型带宽为几百兆赫兹,若使用色散补偿光纤 (DCF),则OEO环的总长度主要取决于DCF(≥8.47km)的长度,振荡模式的间距约为24kHz[4],此时MPF通带中存在大量的振荡模式,因此OEO的跳模效应较为严重。若使用CFBG代替DCF,因为CFBG的长度比DCF的短,所以OEO环的总长度也会缩短,从而增加了OEO振荡模式的间距,抑制了跳模效应。
然而,FIR MPF仍具有相对较大的带宽,通带中包含大量振荡模式。因此,本文利用一个级联的光纤环构成一个IIR滤波器,IIR滤波器与FIR滤波器共同构成一个窄带MPF。当OEO闭环后,缩小的MPF通带中只存在较少的振荡模式,从而有效抑制了跳模效应。
根据文献[9],IIR滤波器的传输函数可以表示为:
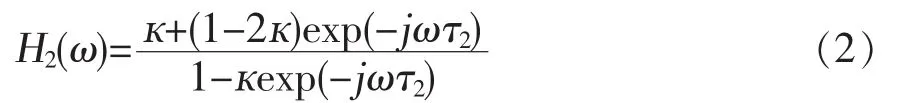
其中,τ2是光纤环的时间延迟,к是光耦合器的耦合比率(本文中к=0.5)。IIR滤波器的自由光谱范围(FSR)为1/τ2,即c /nL2,L2为光纤环长度。由式(2)可以推出IIR滤波器的3dB带宽为0.23c/nL2。由此可以得到整个MPF的传输函数H(ω)=H1(ω)×H2(ω)。
MPF的包络为FIR滤波器的形状,但存在很多由IIR产生的窄周期性边带叠加于包络之上。因此,IIR滤波器的带宽决定了MPF的带宽。由于IIR滤波器带宽较窄,减小了MPF的带宽,使得MPF的通带中只存在极少的振荡模式。
1.2 三阶色散的影响
考虑到CFBG通常比DCF具有更大的TOD且不可忽略,整个MPF的有效包络类似于很多小的MPF包络相互叠加[10]。这些小的MPF形状相似,但有不同的中心频率,其中心频率fc_s可表示为:

当Δτ1增加时,小MPF的中心频率之间的间距会增大,包络会相互分离,从而导致整个MPF变形。当变形严重到一定程度时,MPF无法选择出OEO的振荡频率,即无法使OEO起振。能使OEO起振的MPF中心频率的阈值为:

其中,δ3dB为CFBG的带宽。若MPF中心频率大于fth,则OEO无法起振。因此,OEO的频率可调范围将受限于该阈值。如果CFBG有足够的GVD,并且有较小的TOD或可定制其δ3dB,则fth可以提高,OEO的频率可调范围也随之增大。
1.3 相位噪声特性
利用CFBG代替DCF会对OEO的相位噪声产生很大影响。根据文献[1],OEO的相位噪声由整个OEO环的总长度和输入噪信比(NSR)决定。表征OEO相位噪声功率谱密度的Yao-Maleki公式为[1]:
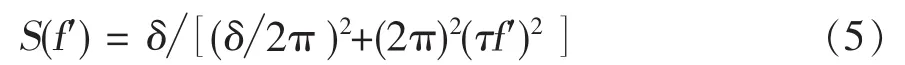
其中,f′为相对于OEO振荡频率的频偏,τ为OEO环的总延时量,δ为OEO的输入噪信比,,ρN为注入OEO的输入噪声密度,为EA之前的总振荡功率。由于CFBG的长度比DCF短,OEO环的总延时会缩短。因此,基于CFBG的OEO相位噪声会比基于DCF的OEO相位噪声高。另一方面,由于CFBG的光滤波效应,CFBG通带外的噪声会被消除,从而使整个链路的噪声减小,输入噪信比δ会随输入噪声功率ρN的减小而减小。因此,OEO相位噪声会降低。由于环长缩短和噪声减小的双重影响,基于CFBG的OEO的最终相位噪声可保持在一个相对较低的水平。
2 实验结果
本文根据图1搭建了实验平台,利用TOF(Alnair Labs CVF-220CL)切割获得的BOS带宽为15nm,CFBG(O/E LAND OEFBG-100)的总GVD为366ps/nm,带宽为3.9nm,整个OEO环的长度为40m。利用矢量网络分析仪(Agilent N5247A)测量MPF的响应,利用EA来保证MPF的增益大于1,EA的增益为60dB,带宽为0.2~14GHz。利用信号分析仪(R&S FSUP)测量产生的微波信号。
当级联一个IIR滤波器时,中心频率为730MHz的MPF的幅度响应如图2所示。IIR滤波器由环长为2.2m的光耦合器组成,其FSR约为90MHz。若不采用IIR滤波器,MPF的带宽大约为300MHz。使用IIR滤波器时,MPF的带宽主要取决于IIR滤波器的带宽,即减小到30MHz内。
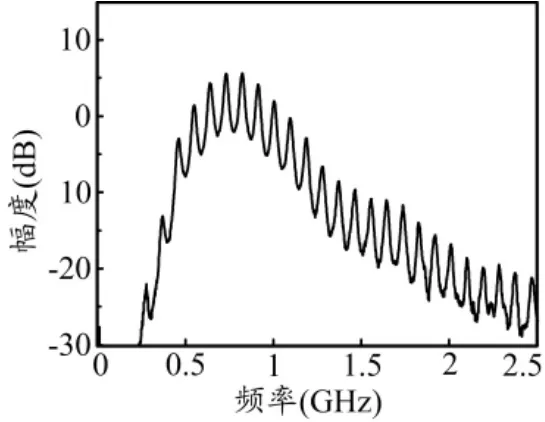
图2 整个MPF的响应
测量OEO振荡产生的730MHz微波信号的频谱图如图3所示。文献[4]中使用DCF时振荡模式的间距为24kHz,图3中,基于CFBG的OEO产生信号的频谱在100MHz范围内约有20个振荡模式,因此其振荡模式的间距约为5MHz,与式(3)计算得到的理论值一致,是使用DCF时的模式间距的200多倍,因此可以有效抑制跳模现象。若仅使用 FIR滤波器,由于 FIR滤波器的带宽(300MHz)与模式间距(5MHz)之间的巨大比率,OEO振荡频率仍会在几个相邻模式间跳动。使用IIR滤波器后,MPF通带中仅存在5~6个模式,此时MPF中心频率的微小变化不能使OEO振荡频率跳跃到相邻的模式上,从而基本抑制了跳模效应。
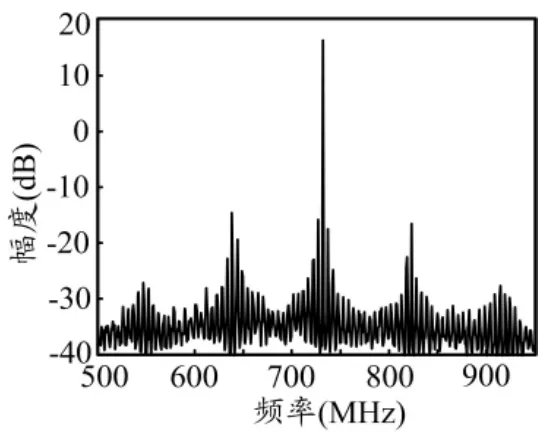
图3 产生的730MHz信号的频谱
OEO振荡频率随时间变化的曲线图如图4所示。当使用DCF时,由于跳模效应的存在,OEO的振荡频率较为不稳定,会在一定范围内跳跃。而基于CFBG的OEO振荡频率比较稳定,无跳模现象,但由于MZI结构会受到外界温度等因素的影响,因此振荡频率会产生微小波动。
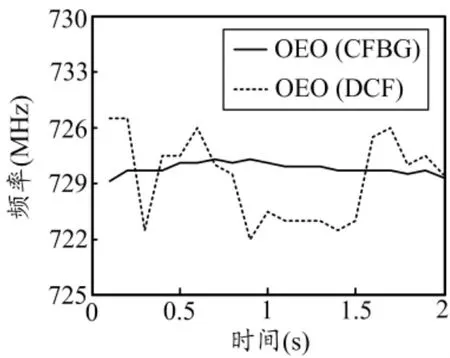
图4 振荡频率随时间变化曲线图
OEO产生的微波信号的相位噪声如图5所示,在10kHz频偏处,相位噪声约为-103dBc/Hz,比文献[4]中使用DCF得到的-110dBc/Hz高。本文通过改变OEO环的长度L1和噪信比δ来估计OEO的相位噪声性能,结果如图6所示。在1kHz频偏处,当δ=10-13、L1= 40m时,使用CFBG的OEO的相位噪声约为-80dBc/Hz,比L1=8.5km,使用 DCF的OEO的相位噪声高 30dBc/Hz。由于CFBG的光滤波效应,光域中的噪声被有效滤除,减小了输入噪信比(δ=10-14),此时使用CFBG的OEO的相位噪声比 δ=10-13时降低了 20dBc/Hz,但仍比采用DCF的OEO高出约15dBc/Hz,这与图5中测得的相位噪声基本相符,从而印证了前文的理论分析。需要注意的是,由于式(5)中仅考虑了理想高斯白噪声的情况,没有考虑实际实验中与频率相关的噪声情况[11],因此,在频偏较高处,仿真结果会出现一定的误差。
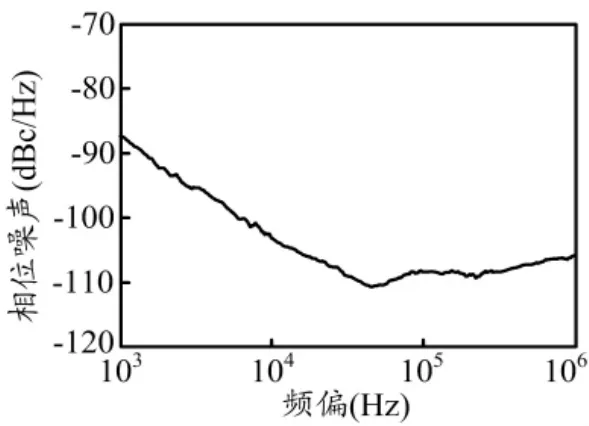
图5 产生的730MHz信号的相位噪声

图6 不同OEO环长和噪信比情况下相位噪声的仿真结果
3 分析与讨论
根据式 (3),OEO的振荡频率可通过可调光延迟线(VODL,MDL-002)来调节,当VODL具有不同延迟量时,MPF的中心频率会发生变化。实验中测得的不同中心频率的MPF(FIR)的幅度响应如图7所示。然而,由于CFBG具有较大的TOD(~240ps3),当中心频率增高时,MPF的变形程度会越发严重,从而限制了OEO的频率可调范围。
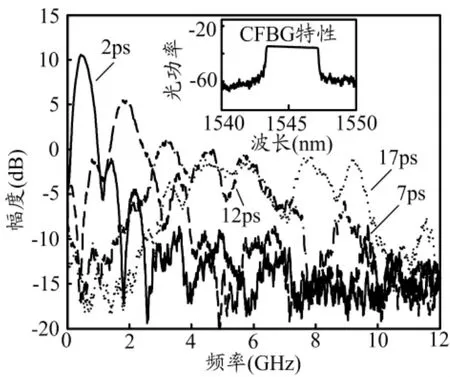
图7 不同VODL延迟量的情况下测得的MPF的响应
对式(1)中的MPF进行数值仿真,仿真参数设置如下:BOS的带宽为3.9nm,总GVD为366ps/nm。仿真结果如图8所示,当TOD为-240ps3时,MPF的变形程度较为严重,随着MPF中心频率的增大,MPF的变形程度会随之增大。在低频处,MPF的变形相对较小,当中心频率足够高时,MPF的变形会非常严重,以致于MPF无法选择出OEO的振荡频率。图7中的实际测量结果与图8中的仿真结果具有较好的一致性。
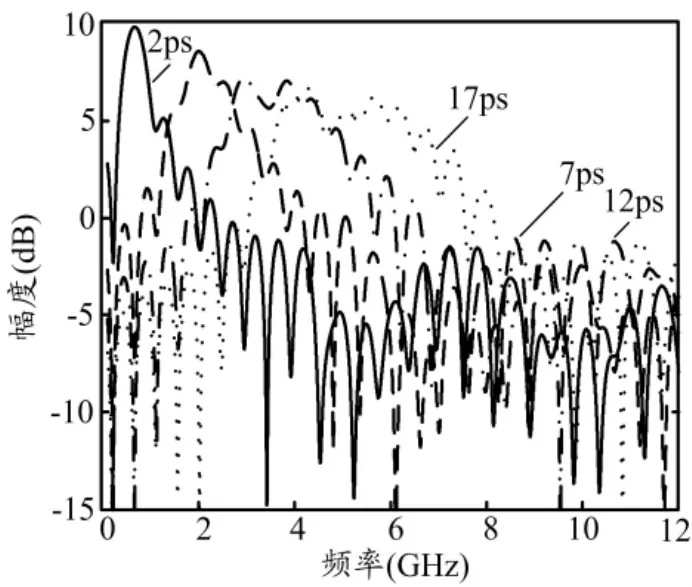
图8 TOD为-240ps3时MPF的仿真结果
若在实验中采用TOD较小的CFBG[12],或利用可编程频谱处理器对TOD进行补偿[12],可以提高OEO的频率可调范围。当TOD为-24ps3时,MPF幅度响应的仿真结果如图9所示,MPF的变形程度较小。我们可以理论预测:当TOD小于-24ps3时,OEO的频率可调范围能达到5GHz以上。
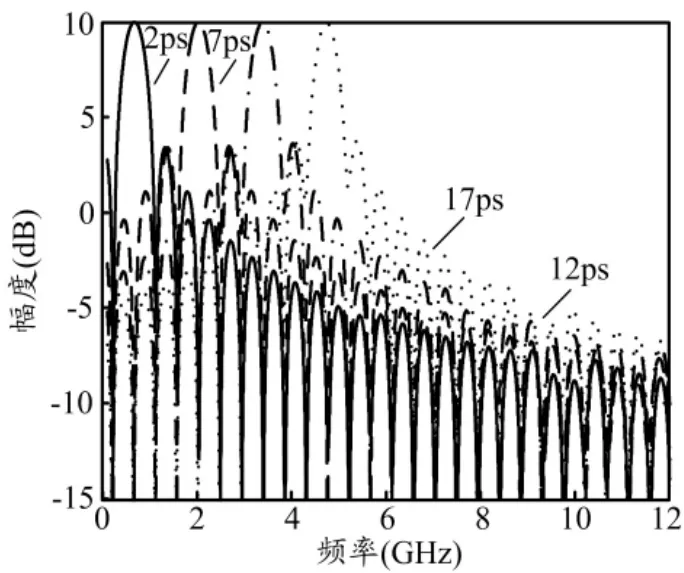
图9 TOD为-24ps3时MPF的仿真结果
4 结束语
本文提出并实现了一种基于MPF的消除了跳模效应的OEO,通过理论和实验证明,利用CFBG代替文献[4]中的长DCF,可以有效增大OEO振荡模式的间距。通过级联一个IIR光纤环,可以缩小MPF的带宽,最终消除OEO的跳模效应,使其振荡频率较为稳定。实验中OEO产生的微波信号的相位噪声在10kHz处为-103dBc/Hz。若能有效抑制CFBG中的TOD,则OEO可在较大范围内动态可调。
[1]YAOX S,MALEKIL.Optoelectronic microwave oscillator[J].J.Opt. Soc.Amer.B,Opt.Phys.,1996,13(8):1725-1735.
[2]KONG F,LI W,YAO J.Transverse load sensing based on a dual-frequency optoelectronic oscillator[J].Opt.Lett.,2013,38(14):2611-2613.
[3]ZHOU W,BLASCHE G.Injection-locked dual opto-electronic oscillator with ultra-low phase noise and ultra-low spurious level[J].IEEE Trans. Microw.Theory Tech.,2005,53(3):929-933.
[4]LIU C,ZOU W,CHEN J.An optoelectronic oscillator based on carrier-suppression-effect-free single bandpass microwave photonic filter [J].IEEE Photonics J.,2013,5(5):1464-1464.
[5]XUE X,ZHENG X,ZHANG H,et al.Widely tunable single-bandpass microwave photonic filter employing a non-sliced broadband optical source [J]Opt.Express,2011,19(19):18423-18429.
[6]YAO X S,MALEKI L.Multiloop optoelectronic oscillator[J].IEEE J. Quantum Electron.,2000,36(1):79-84.
[7]LI W,KONG F,YAO J.Stable and frequency-hopping-free microwave generation based on a mutually injection-locked optoelectronic oscillator and a dual-Wavelength single-longitudinal-mode fiberlaser[J].J. Lightwave Technol.,2014,32(21):3572-3577.
[8]LI W,YAO J.An optically tunable optoelectronic oscillator[J].J. Lightwave Technol.,2010,28(18):2640-2645.
[9]JIANG F,WONG J H,LAM H Q,et al.An optically tunable wideband optoelectronic oscillator based on a bandpass microwave photonic filter[J]. Opt.Express.,2013,21(14):16381-16389.
[10]XUE X,ZHENG X,ZHANG H,et al.Analysis and compensation of third-order dispersion induced RF distortions in highly reconfigurable microwave photonic filters[J].J.Lightwave Technol.,2013,31(13):2263-2270.
[11]LI W,YAO J.A wideband frequency tunable optoelectronic oscillator incorporating a tunable microwave photonic filter based on phase-modulation to intensity-modulation conversion using a phase-shifted fiber Bragg Grating[J].IEEE Trans.Microw.Theory Tech.,2012,60(6):1735-1742.
[12]ERROM J,LASOM A G,BENITO D,et al.Third-order dispersion in linearly chirped Bragg gratings and its compensation[J].Fiber Integrated Opt.,2000,19(4):367-382.
Mode hopping free optoelectronic oscillator based on MPF
JIANG Chen-yan1,JIANG Yuan-yuan2,ZOU Wei-wen1, ZHANG Hao1,LI Shu-guang2,CHEN Jian-ping1
(1.State Key Lab of Advanced Optical Communication Systems and Networks,Shanghai Jiaotong University,Shanghai 200240,China; 2.Shanghai Aerospace Electronic Technology Institute,Shanghai 201109,China)
The paper proposes a mode hopping free optoelectronic oscillator(OEO)based on a microwave photonic filter(MPF).It theoretically analyzes and experimentally proves the effectiveness of eliminating the mode hopping effect by using the chirped fiber Bragg grating(CFBG)and a fiber loop cascaded,analyzes the phase noise performance of the OEO and the three order dispersion of the dispersion medium.
optoelectronic oscillator,microwave photonic filter,chirped FBG,mode hopping effect
TN29
A
1002-5561(2016)04-0019-04
10.13921/j.cnki.issn1002-5561.2016.04.007
2015-12-11。
国家自然科学基金项目(61571292,61535006)资助;“先进航天电子技术”联合实验室项目资助;“区域光纤通信网与新型光通信系统国家重点实验室”自主课题(2014ZZ03016)资助。
蒋琛彦(1991-),男,硕士研究生,主要研究方向为微波光子学。
