过某定点作与双曲线只有一个公共点的直线条数问题

山东省广饶县第一中学　李丽娟

过某定点作与双曲线只有一个公共点的直线条数问题

山东省广饶县第一中学李丽娟

直线与椭圆及抛物线的交点问题相对来说容易理解掌握。因此本文仅对双曲线中过某定点作与双曲线只有一个公共点的直线条数问题加以代数证明，希望对大家有所帮助。

高考数学直线双曲线

圆锥曲线作为高考的热点内容之一，考察频繁。由于不能正确认识交点个数，导致失分。备考时应加强对该问题的理解。直线与椭圆及抛物线的交点问题相对来说容易理解掌握。因此本文仅对双曲线中过某定点作与双曲线只有一个公共点直线条数问题加以代数证明，希望对大家有所帮助。

过定点P与双曲线只有一个交点的直线为双曲线的切线或与渐进线平行的直线。①当P点在双曲线外且不在渐进线上，过P点有两条切线和两条与渐近线平行的直线，共有四条。②当P点在双曲线外且在一条渐进线上，过P点有一条切线和一条与渐近线平行的直线，共有两条。③当P点在双曲线外且在两条渐进线上，即P为原点，过P点没有切线也没有与渐近线平行的直线，有0条。④当P点在双曲线上，过P点只有一条切线和两条与渐进线平行的直线，共有三条。⑤当P点在双曲线内，过P点没有切线，只有与渐进线平行的两条直线，共有两条。

同样几何特征上述结论显然成立，现用代数法予以证明。

证明：与渐进线平行的直线条数只与点是否在渐进线上有关，易证。下面给出切线条数的证明。

设切线过点P且斜率为k，则方程为y=k（x-x0）+y0

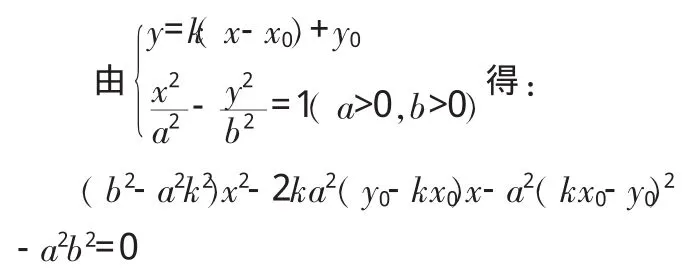
因为切线不可能平行于渐进线，所以b2-a2k2≠0，由直线与双曲线只有一个交点即上述方程只有一解得：

①当P为双曲线顶点时方程（1）无解，这时只有一条平行于y轴（斜率不存在）的直线与双曲线相切，还有两条与渐进线平行的直线，所以与双曲线只有一个交点的直线有三条。②当P在双曲线外且在一条渐进线上时，方程（1）有一解是k=或，显然不可能，只有一条平行于y轴（斜率不存在）的切线，这样过P点只有一条切线，与渐进线平行的直线也只有一条，所以此时与双曲线只有一个交点的直线有两条。③当P在双曲线外且不在渐进线上时，方程（1）有一解，还有一条平行于y轴（斜率不存在）的切线，这样过P点只有两条切线，与渐进线平行的直线也只有两条，所以此时与双曲线只有一个交点的直线有四条。

（2）当 x02-a2≠0时，（此时切线的斜率一定存在，方程（1）有几解就有几条切线），而方程（1）解的情况可由判别式的符号来确定：

①当Δ>0即P在双曲线外且不在渐进线上时，方程（1）有两解，从而过点P可作双曲线的两条切线，还有两条与渐进线平行的直线，所以此时与双曲线只有一个交点的直线有四条。②当Δ>0即P在双曲线外且在一条渐进线上时，方程（1）有两解，但有一解是应舍去，从而过点P可作双曲线的一条切线。且只有一条与渐进线平行的直线，所以此时与双曲线只有一个交点的直线有两条。③当Δ>0即P在双曲线外且在两条渐进线上，即P为原点时，方程（1）有两解为或，都舍去，从而过点P没有与双曲线相切的直线，也没有与渐进线平行的直线，所以此时与双曲线只有一个交点的直线不存在。④当Δ=0即P在双曲线上时，方程（1）有一解，从而过点P可作双曲线的一条切线，还有两条与渐进线平行的直线，所以此时与双曲线只有一个交点的直线有三条。⑤当Δ<0即P在双曲线内时，方程（1）无解，从而过点P没有切线，只有两条与渐进线平行的直线，所以此时与双曲线只有一个交点的直线有两条。

综上，（1）（2）结论得证。