基于梯形和平行四边形的圆片剪冲下料算法设计与实现

陈 燕， 刘 咏， 谢琪琦， 崔耀东

(1. 广西大学计算机与电子信息学院，广西 南宁 530004；2. 华南理工大学工商管理学院，广东 广州 510640)

基于梯形和平行四边形的圆片剪冲下料算法设计与实现

陈 燕1,2， 刘 咏1， 谢琪琦1， 崔耀东1

(1. 广西大学计算机与电子信息学院，广西 南宁 530004；2. 华南理工大学工商管理学院，广东 广州 510640)

提出一种在矩形板材上引入梯形条带来进行排样的方法，首先用两条平行的分界线将板材分为两个大小一致的直角梯形段和一个平行四边形段，分别采用递归算法和动态规划算法确定梯形段和平行四边形段中条带的最优组合，从而确定最优排样方式；再结合线性规划算法解决圆片下料问题，使得整个下料方案的材料利用率最大化。最后采用大量随机生成的例题进行实验，实验结果表明该算法能有效提高材料利用率。

圆片排样；剪冲下料；平行四边形条带；梯形条带

随着资源和能源危机的出现，要求各企业不断提高原材料利用率、减少切割能源消耗，于是研究下料利用率高且切割工艺简单的布局优化算法，切割与装填布局(cutting and packing, C&P)[1]问题越来越受到各制造企业的关注。特别地，圆片下料问题广泛存在机械制造、电机、船舶、航空航天等行业中，例如：电机定子和转子铁心是用硅钢圆片制作而成；家居的锅、壶、盆是用不

锈钢圆片制作的，等等。这些行业每年消耗的金属板材量达千万吨，且原材料费用占生产成本的60%以上，因此提高材料利用率能够为企业带来非常可观的经济效益。将圆片下料技术应用于企业生产实践，能有效地提高下料利用率、节省原材料、提高企业在同行中的竞争力[2]。

近年来，针对圆片条带剪冲下料问题的方法研究，主要有矩形条带进行排样的方法[3-8]和采用平行四边形条带进行排样的方法[9]等。文献中有关矩形条带进行排样的方式也各有不同，其中：文献[3]采用动态规划算法在精确算法的基础上，选取规范长度和规范宽度的子集进行计算，解决剪切阶段的无约束排样问题。文献[4]利用动态规划算法生成T形排样的方式；文献[5]采用动态规划算法生成多段排样的方式；文献[6]采用动态规划算法与枚举法结合生成三块结构的排样方式。文献[7] 和[8]均采用生成四块结构的排样方式，文献[7]的算法是先求解一维背包问题生成块里面的条带最优布局，然后用隐式枚举三条分界线位置得到所有可能的四块组合，选择排样价值最大的四块组合生成最优的四块排样方式；而文献[8]同时使用条带直切排样方式和 T型排样方式，先采用动态规划技术生成排样方式，然后采用基于列生成的线性规划技术迭代调用排样方式生成下料方案。文献[9]基于卷材首次采用平行四边形条带进行排样，通过不断地重复最优的x段和y段，使排样达到全局最优，同时验证了相对于矩形条带排样平行四边形条带排样可以获得更高的材料利用率。卷材的特点是材料长度不受限，根据对多家企业包括宝钢、武钢的板材加工配送中心调查研究，目前实际生产剪裁下料中各企业使用的材料绝大部分是相对固定大小的板材[10]。

本文基于平行四边形排样以获取更高的材料利用率，同时可避免在矩形板材上切割平行四边而产生直角三角形的废料，创新性地引入了梯形条带排样方式。首先在固定大小的矩形板材上用两条平行的分界线将板材切割成两个大小一致的直角梯形段和一个平行四边形段，然后应用平行四边形条带及梯形条带组合排样的三段排样方式。本文算法能保证在整板上切割两刀即可产生最优的平行四边形条带和梯形条带，从而对降低总的生产成本、减少板材大面积损耗概率提供保障。首先分别采用递归算法和动态规划算法确定梯形条带和平行四边形段中条带的最优组合，从而确定当前的最优排样方式；然后应用线性规划(linear programming, LP)方法求解圆片剪冲下料问题 (cutting stock problem of circular blanks, CSPCB)，使得整个下料方案的材料利用率接近最优；最后通过与其他采用固定大小板材进行排样的算法实验说明本文算法对板材利用率的提高，同时分析条带中排入毛坯行数对材料利用率的影响，还分析了算法的时间复杂度和计算产生最优排样方案所消耗的时间。实验数据表明，本文算法是有效性的、计算时间是可接受的。

1 排样方式算法原理及其实现

1.1 相关概念

1.1.1 毛坯在条带上的排列、条带方向和长度

本文算法在矩形板材上同时应用平行四边形条带和直角梯形条带进行排样，平行四边形条带可以是X向或Y向，梯形条带只允许X向条带。如图1(a)中的箭头方向表示该条带是X向，图1(b)中的箭头方向表示该条带是Y向，X向条带中毛坯是从左至右依次排放；Y向条带中毛坯是从下至上依次排放。平行四边形Y向条带可由平行四边形X向条带旋转60°得到。

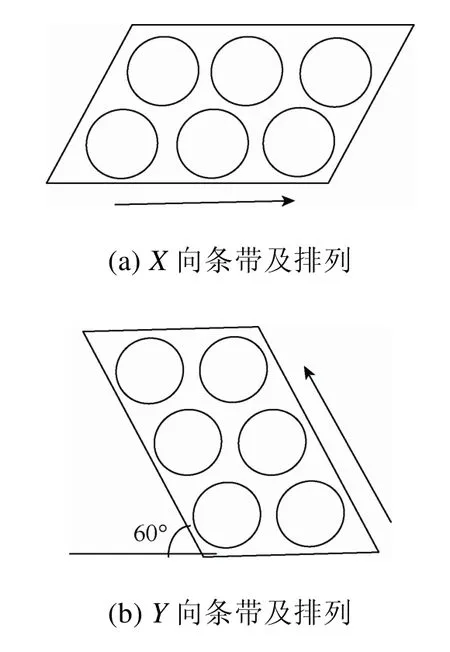
图1 条带方向及毛坯排列

每根条带包含一排或者多排直径相同的圆片，如图2所示，d为圆片直径，相邻圆片边界距离为w，即为工艺余量，圆片离条带边界的距离为w/2，相邻两排圆片间的距离为，平行四边形条带和梯形条带的底角均为60°。

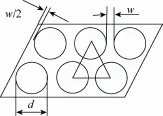
图2 双排条带

图3(a)为平行四边形条带排列示意图，sh为平行四边形中与条带方向垂直的高度，ps为平行四边形中不与条带方向平行的底边长度。图3(b)所示为梯形条带排列示意图，其中bt表示梯形条带下底边的长度，ut表示上底边的长度，ts表示条带的高，毛坯在条带中的排列是从斜边底部开始，依次向直角边进行排放。

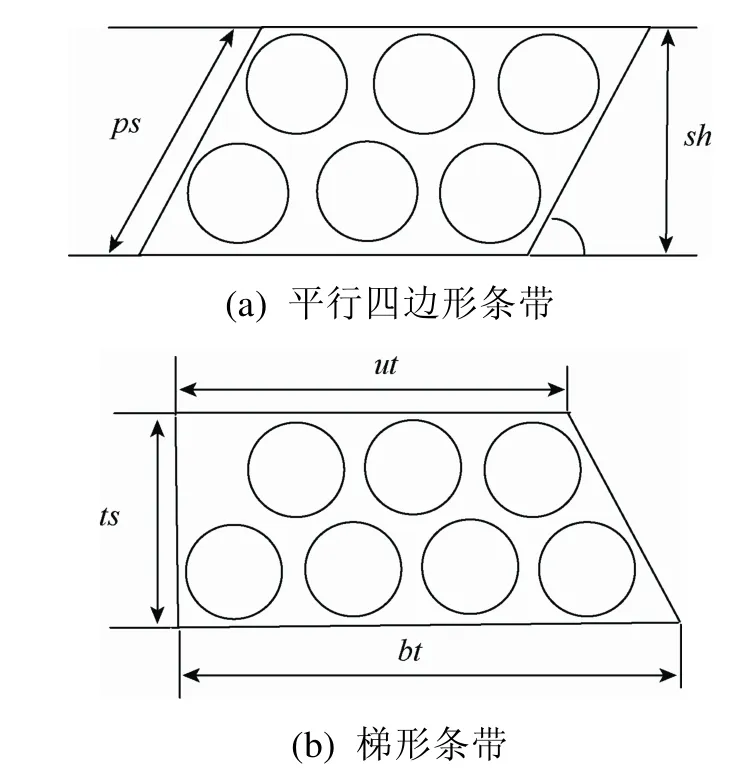
图3 平行四边形条带及梯形条带

1.1.2 条带宽度和价值

平行四边形条带的宽度是与条带底边方向成60°的的长度，即图3(a)中ps边长；梯形条带的宽度是梯形的高，即图3(b)中ts边长。记gi(若无说明i取值范围均为1≤i≤k，k为需求毛坯种数)为第i种毛坯的条带中允许的最大排数，其中第j(若无说明j取值范围均为1≤j≤gi)种条带包含有j排毛坯。

(1) 平行四边形条带的价值计算。由图 2及图3(a)可得，则平行四边形条带宽度：，记vi为第i种毛坯的单个毛坯价值，条带的价值即是条带中所有毛坯的价值总和。如图4所示，pd是平行四边形条带能包含至少一个毛坯的条带长度。当第 i种毛坯的条带长度为x时，若其中包含有j排毛坯，根据以下步骤计算平行四边形条带价值：

图4 平行四边形条带初始长度

由几何规则可知

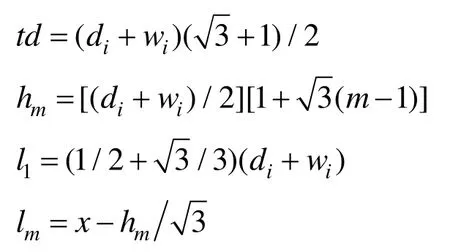
条带中第m排毛坯的个数

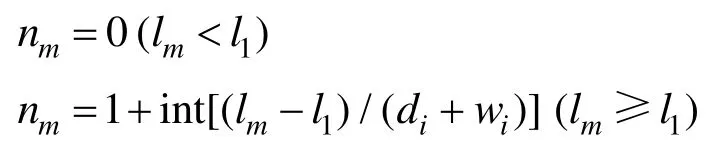
若x＜td，条带中毛坯个数n=0；若x≥td，条带中毛坯个数，所以梯形条带价值为tt=nvi。

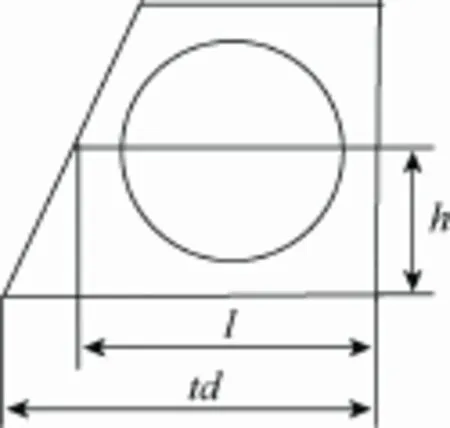
图5 梯形条带初始长度

如图6所示，两条与底边成60°的切割线将板材分为 3个部分，两个梯形段大小一致，中间部分是平行四边形段。切割起点距板材宽的距离为y的切割线，且称之为分隔线y。每个段中的条带方向都是一致的，梯形段中的条带都是 X向，平行四边形段中的条带是X向或Y向。记排入梯形段中所有毛坯价值总和的最大值为 ZT(bl,W )，其中W 是板材的宽度，bl为梯形段底边的长度，可由计算得出。记排入平行四边形段中所有毛坯价值总和的最大值为 ZP(pl,p w)，其中，同时称相对应的平行四边形为pl×pw。由几何规则可知y的取值范围为。若排入平行四边形段的条带方向是 X向，则此时该段的最大价值为Zx(pl,p w)；若排入的条带方向是y向，此时该段的最大价值为 Zy(pl, pw)，因此平行四边形段的最大价值。整个板材中毛坯的最大价值 z(y) =2 ZT(bl,W)+ ZP(pl, pw)，若对于所有的y，都有 z(y0)≥ z(y)，则记y0为最优分割线。

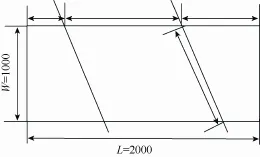
图6 板材切割示意图

1.2.1 梯形排样算法

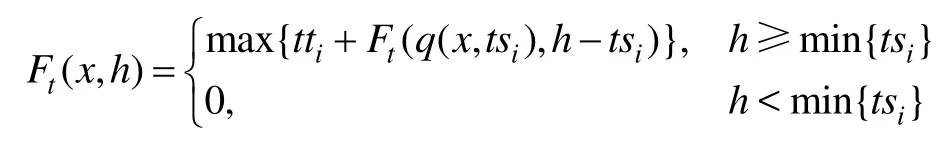
设递归函数Rec(bl,W)返回下底长为bl高为W的梯形段的最大价值，其步骤如下：

步骤1. 如果Ft(x,h)≥0，转向步骤6；否则转步骤2。

步骤2. 令Ft(x,h)=0，i=1，得到当前梯形条带当前价值向量TT。

步骤3. 如果 h＜tsi，转步骤5；否则，令ut= q(x,t si)，令 V =tti+ Rec(ut,h -tsi)。

步骤 4. 如果 V≤Ft(x,h)，转步骤 5；否则令Ft(x,h)=V。

步骤5. 令i=i+1。如果i≤M，转步骤3；否则转步骤6。

步骤6. 返回Ft(x,h)。

1.2.2 平行四边形排样算法

在图6的平行四边形段pl×pw中，假定条带方向和pl方向一致，根据1.1可分别计算出平行四边形中的条带宽度向量PS和价值向量PT，平行四边形段的最大价值由以下数学模型求解

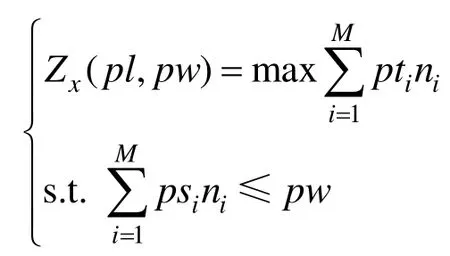
其中，ni为正整数，i=1,2,··,M

该模型是一个背包问题，可通过下面的背包函数求得问题的解

同理可求得 Zy(pl,pw) ，令 ZP(pl,p w)= max{Zx(p l,p w),Zy(p l,p w) }。

1.2.3 板材最优排样方式生成算法

步骤1. 根据板材大小L×W得到ymax及pw的值，初始化PS、TS，令i=0。

步骤2. 根据i得到bl、pl的值，得到PT。

步骤3. 根据1.2.1得到梯形段最大价值ZT(bl,W)。

步骤4. 根据1.2.2得到平行四边形段最大价值ZP(pl, pw)。

步骤6. 令i=i+1，若 i≤ymax，转步骤2；否则输出y0、z0及当前排样P。

2 下料方案生成算法

2.1 圆片下料问题的线性规划模型

圆片剪冲下料问题CSPCB可描述为：对库存板材进行剪冲下料，以满足k种圆片毛坯的需求，其中第i种毛坯的需求量为bi，i=1,2,··,k。问题求解要求确定一种最优下料方案，使得在满足所有毛坯需求的前提下，所消耗的板材张数最少。

采用LP方法求解该问题的数学模型为

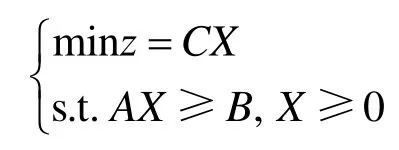
其中，C为板材的价值向量，C=[c1,c2,··,cn]，n为排样方案包含排样方式的个数，若下料时只用到单一规格的矩形板材，则cj=L×W(j=1,2,··,n)，L和W分别为矩形板材的长度和宽度；X=[x1,x2,··,xn]T，xj(j=1,2,··,n)为下料方案中应用每种排样方式的次数；z为其中一种下料方案所消耗的板材的总价值；B=[b1,b2,··,bk]为毛坯的需求数量的列向量；A 为k行n列的记录各种排样方式的矩阵，其元素aij(i=1,2,··,k，j=1,2,··,n)表示第 j种排样方式中包含第i种毛坯的个数。矩阵中每一个列向量即记录一种排样方式中用到的各毛坯的数量。

可用列延迟生成法解上述模型，具体步骤如下：

(1) 确定初始可行解。初始化A为一个单位矩阵，则初始可行解X=B。

(2) 修改毛坯的当前毛坯价值向量 V，V=CA–1。

(3) 求解使目标函数改善的排样方式。根据1.2.3得到当前排样方式P。若LW–VP＜0，则引入P改善矩阵A，用引入的P替换A中的第q列，q可根据单纯形法求得，并令cq=LW，转步骤2。若LW–VP≥0，则当前下料方案已是最优，结束循环。

2.2 圆片下料方案的算法实现

针对用线性规划模型求解CSPCB问题，本文提出以下算法实现解决方案：

Begin

初始化板材大小、毛坯的各参数及初始可行解X；

确定当前毛坯的价值向量V=CA–；

令value=L×W+1；

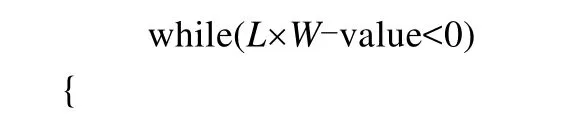
调用排样方式生成算法，value=z0；

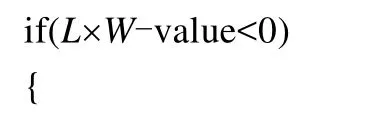
记录当前排样方式P；

根据单纯形法确定q，用P替换A中的第q列；

求解X，重置当前毛坯价值向量V=CA-；

将X中的元素向上取整；

End

3 实验结果

在Mirosoft visual studio 2013平台上用C#语言编程实现算法，在主频为2.60 GHz，内存为8 GB的计算机上进行实验。

3.1 算法对材料利用率的提高

材料利用率 U=(所需毛坯的总面积/消耗板材的总面积)×100%。本文实验采用文献[4]的变量取值范围，如表1所示。随机生成500个测试样例与文献[4]中的 T形排样算法作比较，本文算法得到的平均材料利用率为70.81%，而文献[4]中T形排样算法得到的平均材料利用率为 68.46%。两者相比，本文算法的平均材料利用率约高出 2个百分点，说明本文算法更有利于提高生产的经济效益。

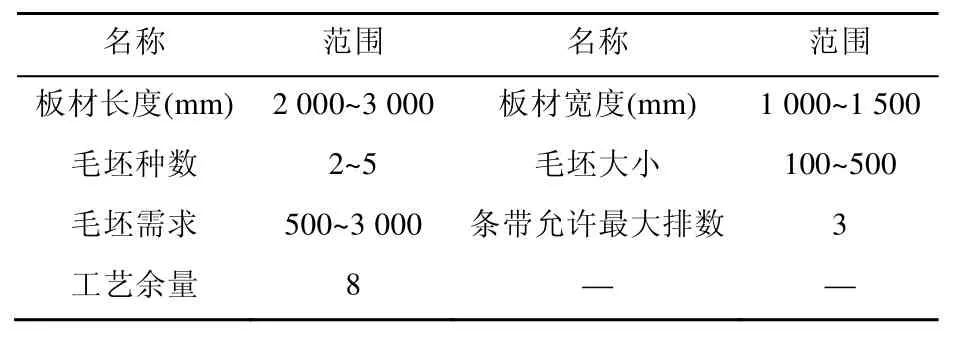
表1 参数取值范围

3.2 参数对材料利用率的影响

本文还对条带中允许排入毛坯的最大排数对材料利用率的影响进行了研究。参数的取值范围参照表 1，其中条带允许最大排数分别取为 1，2，··，6，取为1时表明一根条带中只能有一行毛坯，取为 2时表明一根条带中可以包含一行毛坯也可以包含两行毛坯，以此类推。分别用这些参数各随机生成 100个测试样例，其平均材料利用率的结果如表2所示。

由实验结果可知，增加条带中允许的毛坯排数可以提高材料利用率，在排数小于等于 3时，材料利用率的提高较为明显；当排数大于 3时，材料利用率的提高不明显，因此本文算法建议允许的条带排数不超过3。

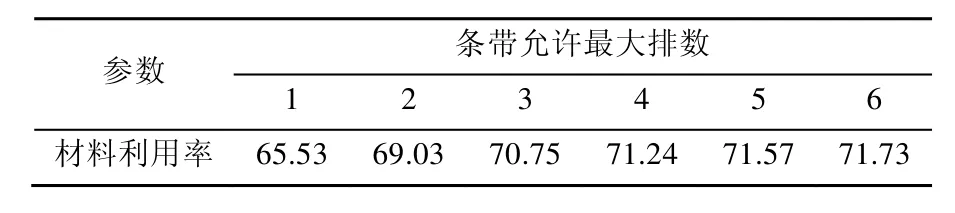
表2 条带排数对材料利用率的影响(%)

3.3 求解一个真实的下料案例

板材大小为2000×1000，需求毛坯有8种，其直径大小分别为362，297，102，153，148，352，198，244，需求数量分别为2 672，532，2 775，1 034，1 216，1 786，1 515，2 522，工艺余量为8。程序求解耗时43.23 s，下料方案如图7所示，总共消耗了483块板材，一共有8种排样方式，材料利用率为73.68%。

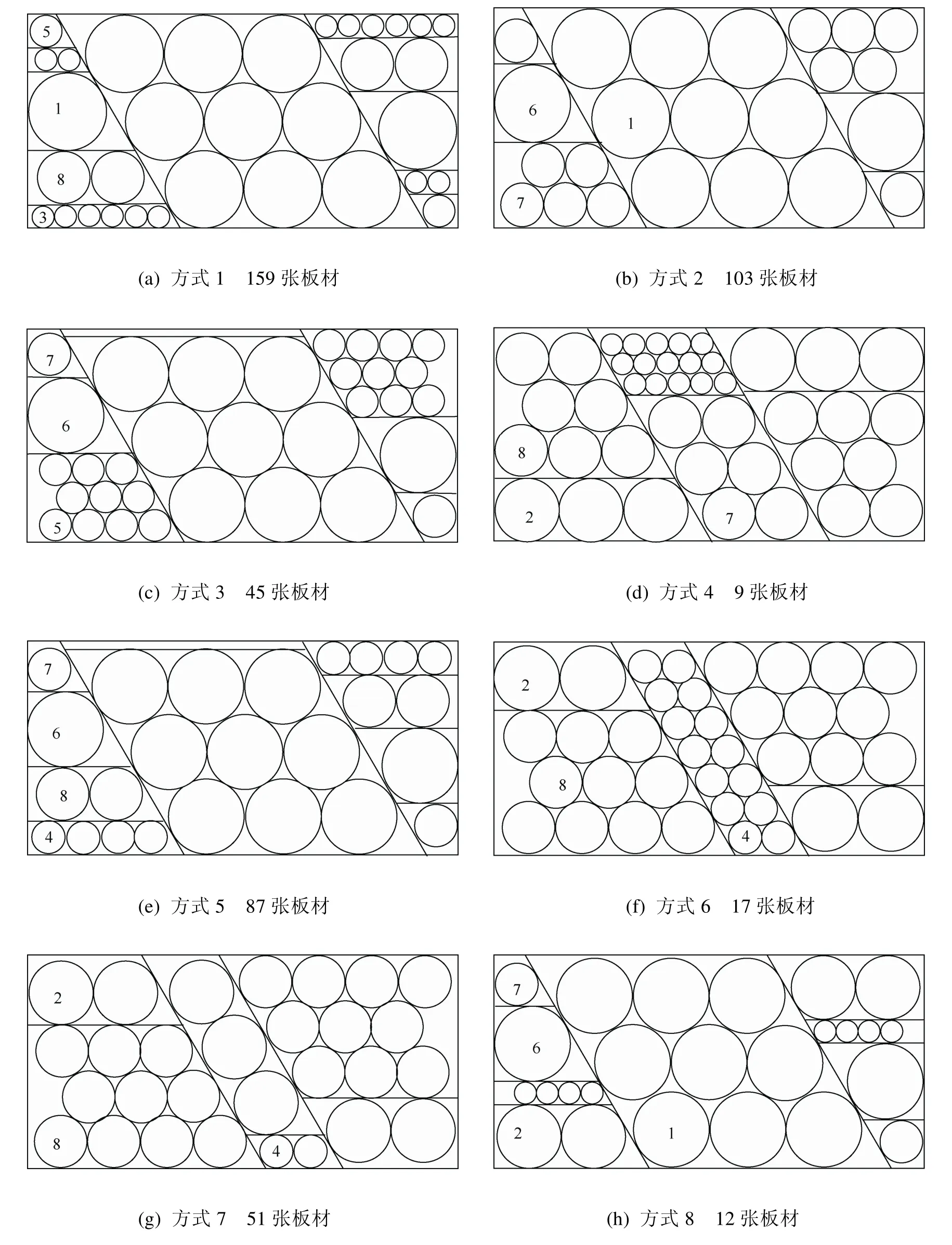
图7 下料方案图例

3.4 算法时间复杂度分析

算法的效率一般用时间复杂度来衡量，时间复杂度可以描述算法执行基本运算的次数。对于CSPCB问题，基本运算可以看成是一个排样方式的生成。本文用单纯形法求解线性规划问题，最坏情况下的时间复杂度是指数级别的，所以需用排样方式生成算法的时间复杂度来判断算法的优劣性。对于算法1.2.1，T(n)=T(n–1)+O(1)=O(n)，则时间复杂度为O(MW)；对于算法1.2.2，背包体积为L，物品种类个数为M，则动态规划算法解决该问题的时间复杂度为 O(ML)。则排样方式生成算法1.2.3的时间复杂度为 O(ML2)。在随机生成的 500个样例的实验中，平均每个问题的计算时间是53.526 s。

CSPCB是一个NP难问题，在有限的时间内只能得到一个接近最优的解。本文算法相对于其他算法在时间上没有显著的改善，但是在材料利用率上有较大的提高。实际生产中，一个生产计划的下料方案在计算出来之后就不会改变，本文算法所消耗的时间在可接受的范围之内。

4 结 论

本文提出在矩形板材上引入梯形条带排样方式，可以利用平行四边形排样以获取更高的材料利用率，同时又可以利用在矩形板材上切割平行四边产生的直角三角形废料。实现了梯形排样和平行四边形排样的算法，用于求解实际的板材下料问题。实验计算结果表明，应用平行四边形条带和梯形条带组合排样的算法比 T形排样算法获得更高的材料利用率；实验结果还证明了毛坯行数在 3~4行时材料利用率提高得较为明显，最后通过实验图给出一个完整的下料解决方案。

[1] 潘卫平, 陈秋莲, 崔耀东, 等. 基于匀质条带的矩形件最优三块布局算法[J]. 图学学报, 2015, 36(1): 7-11.

[2] 崔耀东. 计算机排样技术及其应用[M]. 北京: 机械工业出版社, 2004: 82.

[3] 杨 剑, 黄少丽, 侯桂玉, 等. 圆片剪冲下料排样算法[J]. 计算机工程与设计, 2010, 31(23): 5139-5142.

[4] Cui Y D. Generating optimal T-shape cutting patterns for circular blanks [J]. Computers & Operations Research, 2005, 32(1): 143-152.

[5] Cui Y D. Generating optimal multi-segment cutting patterns for circular blanks in the manufacturing of electric motors [J]. European Journal of Operational Research, 2006, 169(1): 30-40.

[6] 陈 菲, 刘 勇, 刘 睿, 等. 基于3块方式的圆形片剪冲排样算法[J]. 计算机工程, 2009, 35(14): 195-197.

[7] 王 岩, 潘卫平, 胡 钢. 生成圆形片最优四块排样方式的确定性算法[J]. 机械设计与制造, 2014, (9): 152-155.

[8] 王 峰, 张 军, 胡 钢. 圆形片剪冲下料问题的一种求解算法[J]. 锻压技术, 2015, 40(10): 39-44.

[9] Cui Y D, Song X X. Applying parallelgrammic strips for cutting circles from stainless steel rolls [J]. Journal of Materials Processing Technology, 2008, 205: 138-145.

[10] Cui Y D, Chen Y Y, Wu J L. Selecting the best sheet length for the steel stock used in circular blank production [J]. Iie Transactions, 2006, 38(10): 829-836.

An Algorithm for Circle Cutting Stock Problem Based on Trapezoid and Parallelogram

Chen Yan1,2, Liu Yong1, Xie Qiqi1, Cui Yaodong1

(1. Department of Computer and Electronic Information, Guangxi University, Nanning Guangxi 530004, China; 2. School of Business Administration, South China University of Technology, Guangzhou Guangdong 510640, China)

A pattern of circular cutting in rectangle sheet is proposed by introducing trapezoidal stripes. Plate with two parallel dividing lines will be divided into three segments when the nesting, two segments of the same size right angle trapezoid and one parallelogram segment. Respectively recursive algorithm and dynamic programming algorithm are used to determine the optimal combination of stripes in trapezoidal section and parallelogram section, so as to determine the optimal pattern. Then combine with linear programming algorithm to solve the problem of the two-dimensional cutting pattern problem, making material utilization maximum. Finally, experiment results of a large number of randomly generated problems show the effectiveness of improving material utilization of the algorithm.

circular cutting pattern; shearing and punching; parallelogram stripes; trapezoidal stripes

TH 164

10.11996/JG.j.2095-302X.2016050661

A

2095-302X(2016)05-0661-07

2016-01-06；定稿日期：2016-03-20

国家自然科学基金项目(61363026，71371058)

陈 燕(1975–)，女，广西北流人，教授，博士研究生。主要研究方向为高性能计算、算法优化设计与实现、计算机辅助设计等。

E-mail：gxcy@foxmail.com