浅谈解中考几何题的一些想法

王慧

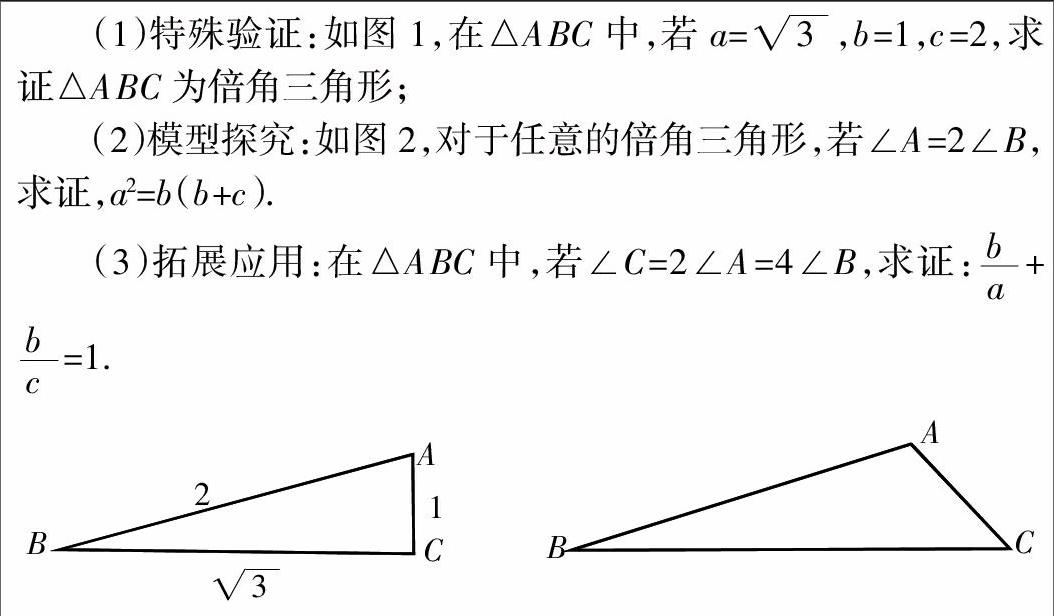
一、例题展现

新知认识：在△ABC中，∠A，∠B，∠C所对的边分别用a、b、c表示，如果一个三角形的一个内角等于另一个内角的两倍，我们称这样的三角形为“倍角三角形”。

[试题评析]：本题要求学生应用新定义探索解决问题，需要学生阅读题目给出的相对于学生来说是新知识材料，并在理解的基础上加以运用，以解决新问题。考查了学生自己阅读材料获取新知识，学习理解新知识和应用新知识的能力，考查层次丰富，不同水平学生可以充分展示自己不同的探究深度，考查了学生综合运用数学知识、思想方法去探索规律、获取新知的能力。试题在知识迁移的同时关注方法迁移，而且是多题一解，让学生经历学习、探索、问题解决的整个过程。这里将考试过程与学习过程结合起来，体现了一种较好的理念。借助问题解决的过程实现对所直接考查知识和技能的再抽象到一般意义下该能力和思想方法的考查，考题显现出新的问题模式策略，对于改进、提高中考的科学有效性具有积极作用。

二、几何命题核心素养考查的分析与展望

1.关注图形概念、性质与变化，促进空间观念的发展。各地市基本保持对物体三视图的考查。同时几何图形的概念、性质、判定知识是空间观念中最基础、最重要的内容。还有通过图形的运动形式和运动方向两个维度的考查，关注了学生空间观念的形成与发展。今后对空间观念的考查，仍将以传统的考查方式为主流方向。

2.关注几何图形的应用与变换，深化几何直观的价值与本质。几何直观所指的有两点：一是几何，指的是图形；二是直观，指的是依托，利用图形进行数学的思考、想象。体现在考题上一是能否正确画图，考查几何直观的基础——图形表示，二是通过对图形的分析思考，实现对数与形之间的化归与转化的考查，考查几何直观的应用层面——图形分析与图形思考。几何变换在平面几何中占有重要位置，变换是研究几何图形性质的重要手段和方法，是培养学生几何直观和合情推理的好方法。借助图形变换呈现图形的特性及图形的生成过程，从而实现对图形性质与判定的全面考查，相信是今后的命题热点。

3.保持演绎推理的考查，强化对合情推理的考查。各地一直都关注对演绎推理的考查，几何推理借助三角形、四边形、圆等基本图形，直接考查学生的推理能力。在压轴题中设置“猜想—证明”的情境进行探索问题，考查用合情推理发现结论、用演绎推理证明结论的完整过程，深化对数学基本思想的考查，是强化推理能力考查的重要方式。这类试题常由特殊图形、特殊位置出发探索结论，随着图形一般化，提出猜想并论证、应用；这样的问题设置体现了一个从认识、理解、解释到应用与拓展的完整数学学习过程，突出考查学生的推理能力，对初中数学教与学都起到一个良好的导向作用。

三、中考命题的坚守与展望

1.教材是承载课标理念的载体，是连接“教”和“学”的媒介，更是命题的核心素材。在命题中要充分挖掘教材例、习题的潜在功能。试题可直接取材于教材，但要经过精心改造，凸显“用”教材的明确导向，进一步矫正“教”教材、题海战术等不良行为。

2.关注新知识的定义、理解与应用，进一步强化数学应用意识，适度关注创新意识的考查。学生应用新定义探索解决问题，需要学生阅读题目给出的相对于学生来是新知识的材料，并在理解的基础上加以运用，以解决新问题。考查了学生自己阅读材料获取新知识，学习理解新知识和应用新知识的能力。试题在知识迁移的同时关注方法迁移，从而让学生经历学习、探索、问题解决的整个过程。

3.关注初高中数学知识的衔接，关注与高中后续学习能力的有机承接。这类试题考查的关键不是知识本身，而是研究知识的方法与工具。但若试题只是过度追求知识的衔接，问题设置只停留在低层次的方法模仿，这样的命题策略值得商榷。

4.关注问题情境的设立，寓教育于问题之中。眼界远比知识重要，当数学文化的魅力真正渗入教材、进入课堂、融入教学时，数学就会更加平易近人，数学教学就会通过文化层面让学生进一步理解数学、喜欢数学，在数学学习中体验数学思考的乐趣和文化魅力，提升科学素养和人文素养。要求在命题过程中关注问题的趣味性、生活性、应用性、文化性、教育性、时代性。

5.数学活动经验的积累是提高学生数学素养的重要标志.。通过设置开放型、操作型、探究型等具有过程性特征的试题，多角度、多层次立体考查学生对解决问题和分析问题的基本数学活动经验积累情况的考查，感悟数学的理性精神，形成创新能力。

开放型试题，可以培养考生的问题意识，让考生充分展示不同的思维品质与个性特征。

探究型试题将数学问题活动化，试题通过设计一个类似数学探究活动的情境，从对特殊的问题验证入手，有意识地强化基本图形的运用，将问题进行拓展应用，展现问题解决的过程和方法，突出对数学活动经验的考查。

操作型试题所设置的问题基于实验与操作的前提，常以裁剪、折叠、拼接为载体，通过观察、分析、猜想、试验、推理、反思等系列活动，让考生经历了直观感知、操作确认、推理论证的过程。这种命题方式使问题的展开方式和过程有助于考查学生数学学习经验的积累，而且对于改进、引导教法和学法也有积极意义。

参考文献：

[1]侯方莹.初中数学中考几何体型研究分析[J].新课程（中学），2016（2）.

[2]安红琴.对中考数学动态几何题地探究[J].理科考试研究，2012（12）.