管涌型尾粉砂临界水力梯度计算方法探讨

陈定安，于沉香

(中国冶金科工集团公司 武汉勘察研究院有限公司，武汉 430080)



管涌型尾粉砂临界水力梯度计算方法探讨

陈定安，于沉香

(中国冶金科工集团公司 武汉勘察研究院有限公司，武汉 430080)

尾粉砂的结构构造特点决定了其临界水力梯度大于常规的砂性土，按常规计算公式得到的管涌型尾粉砂的临界水力梯度计算值远小于实测值，因此，常规土的临界水力梯度计算方法并不适用于尾粉砂。通过收集整理尾粉砂的物理与颗粒特征指标，对比分析流土型与管涌型尾粉砂的颗粒级配特征，得到尾粉砂产生管涌的颗粒级配条件。在分析尾粉砂颗粒形态特征、颗粒级配特征、孔隙特征与临界水力梯度之间的关系的基础上，用特定的尾粉砂试样测定发生管涌时的临界水力梯度与孔隙率(比)之间的函数关系，进而导出尾粉砂发生管涌的临界水力梯度的计算通式，最后通过室内试验检验按计算通式计算结果的可靠性。相关试验检验表明，该计算通式的计算结果与室内实测结果基本吻合，可用来估算尾粉砂发生管涌的临界水力梯度，估算值略偏于安全。

尾粉砂；管涌；临界水力梯度；颗粒级配；孔隙率

1 研究背景

管涌是指在渗流作用下土体中的细颗粒在粗颗粒形成的孔隙孔道中发生移动并被带出，逐渐形成管形通道，从而淘空地基或坝体，使地基或斜坡变形、失稳的现象[1]。渗透压力的存在降低了坝坡的整体稳定性，尾矿体在渗流作用下也可能产生自身的变形和破坏[2-3]。一般管涌多发生在非黏性土中，其特征是：颗粒大小比值差别较大，往往缺少某种粒径，磨圆度较好，孔隙直径大而且互相连通，细粒含量较少，不能全部充满孔隙，颗粒多由相对密度较小的矿物构成，易随水流移动，有较大和良好的渗透水流出路等[4]。朱崇辉等[5-7]从渗透试验中发现随着粗细颗粒级配的不同，土的渗透机理将发生改变，土的渗透破坏性质取决于粗颗粒的特征，因此建议将级配特征参数引入渗透破坏模型公式，建立分段统一的渗透破坏坡降模型表达式。

《水利水电工程地质勘察规范》(GB50287—2008)给出了常规土发生管涌的临界水力比降Jcr的计算公式为

(1)

式中：γ′和γw分别是土的浮重度和水的重度；Gs为尾粉砂的相对密度；n为土的孔隙率；d5，d20分别为占总土重5%和20%的土的粒径(mm)。

将管涌型尾粉砂相关物理指标代入式(1)计算的临界水力梯度远小于实测值(见表1)。

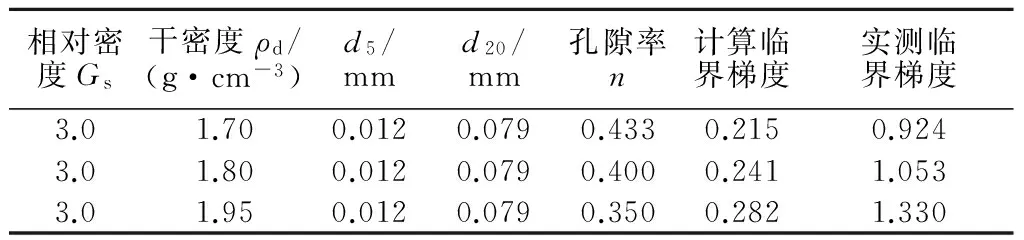
表1 管涌型尾粉砂临界水力梯度对比

构成尾矿堆积坝的细粒尾矿分别是尾粉砂、尾粉土、尾粉质黏土及尾黏土4类，与天然土相比，这4类尾矿只有尾粉砂的结构具有能形成管涌的部分特征。实体工程案例与室内试验证明，在某些级配条件下，尾粉砂在动水压力作用下，确实能产生管涌型渗透变形。

尾粉砂与天然土相比，磨圆度差，颗粒基本呈棱角状，分选性差，相对密度大，级配连续，主要粒组含量分布在0.075～0.25 mm，黏粒含量1%～15%，颗粒直径分布范围窄，孔隙率大多在0.35～0.55之间。尾粉砂在动水压力作用下，抵抗管涌发生的能量主要由能移动的颗粒浮重力与孔隙通道对能移动的颗粒摩阻力构成。尾粉砂的结构构造特点决定了尾粉砂的临界水力比降大于常规的砂性土。式(1)考虑了颗粒的浮重力变化，造成计算结果远小于实测值是由于常规土的孔隙阻力分量计算方法不适用于尾粉砂。

2 试验研究

尾粉砂抗渗临界水力梯度的高低，取决于其悬浮颗粒的密度大小与孔隙通道对移动颗粒的摩阻力大小。

2.1 尾粉砂产生管涌的级配条件

孔隙通道对移动颗粒的摩阻力大小与尾粉砂的颗粒形状、粒组级配特征及尾粉砂堆积体的孔隙大小有关。尾矿是人工破碎土，经过短距离管送，颗粒形状一致，基本是棱角状，可略去颗粒形状因素对其临界水力梯度的影响，只研究孔隙大小、颗粒级配特征与临界水力梯度的关系。

笔者收集整理了40座上游法尾矿堆积坝4 000余组尾粉砂的物理与颗粒分析特征指标，并对比了总体呈流土型与管涌型尾粉砂的颗粒级配特征。研究发现：①上游法尾粉砂堆积体的孔隙率大小与其相对密度没有关联，只与其堆积方式有关(见图1)；②流土型与管涌型尾粉砂不均匀系数与黏粒含量之间均呈明显的指数函数关系，且管涌型尾粉砂黏粒含量不大于8%(见图2)；③管涌型尾粉砂不均匀系数基本在10以下(见图3)。

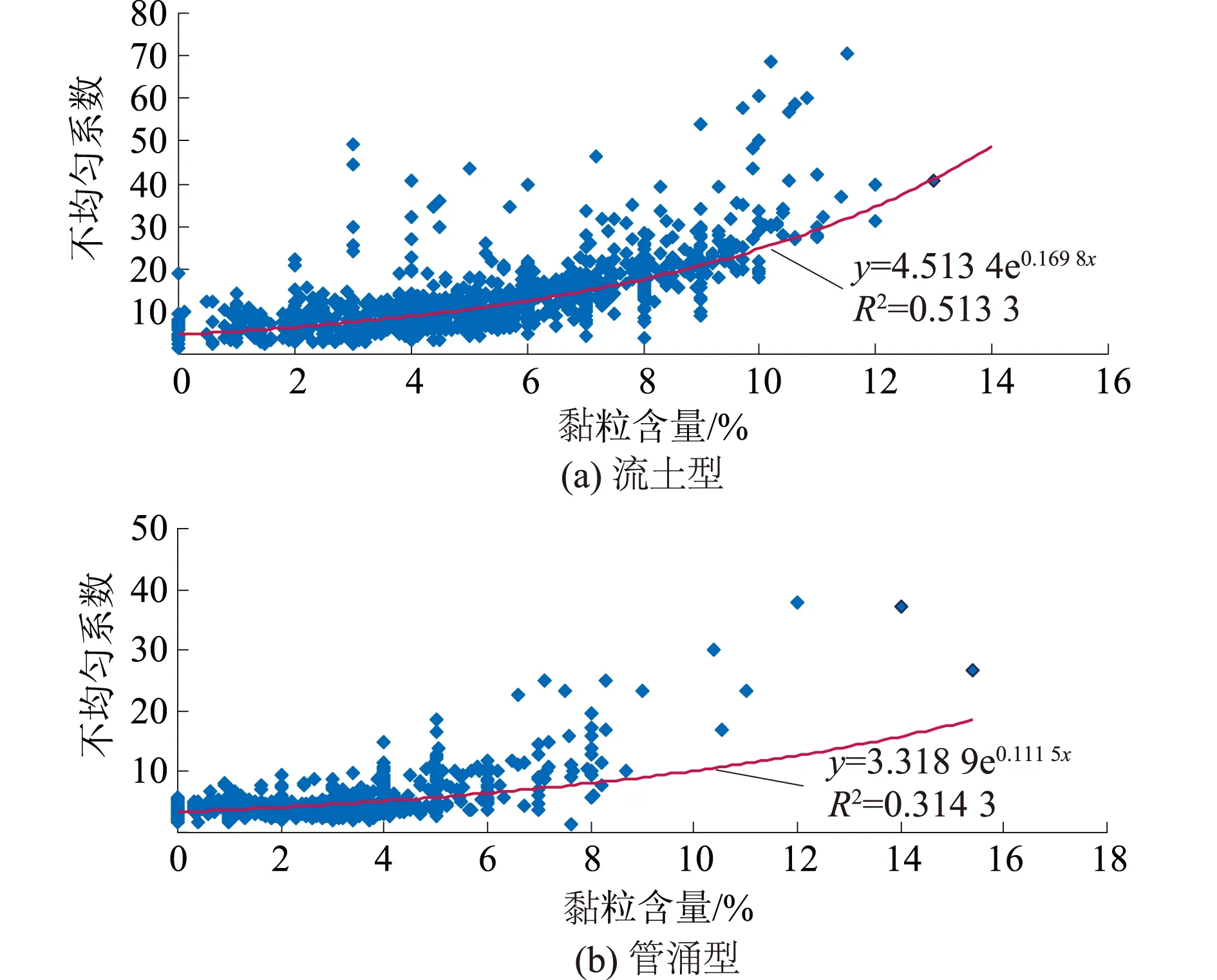
图2 尾粉砂不均匀系数与黏粒含量散点图Fig.2 Scatter diagram of the uniformity coefficient and clay content of tailing silt

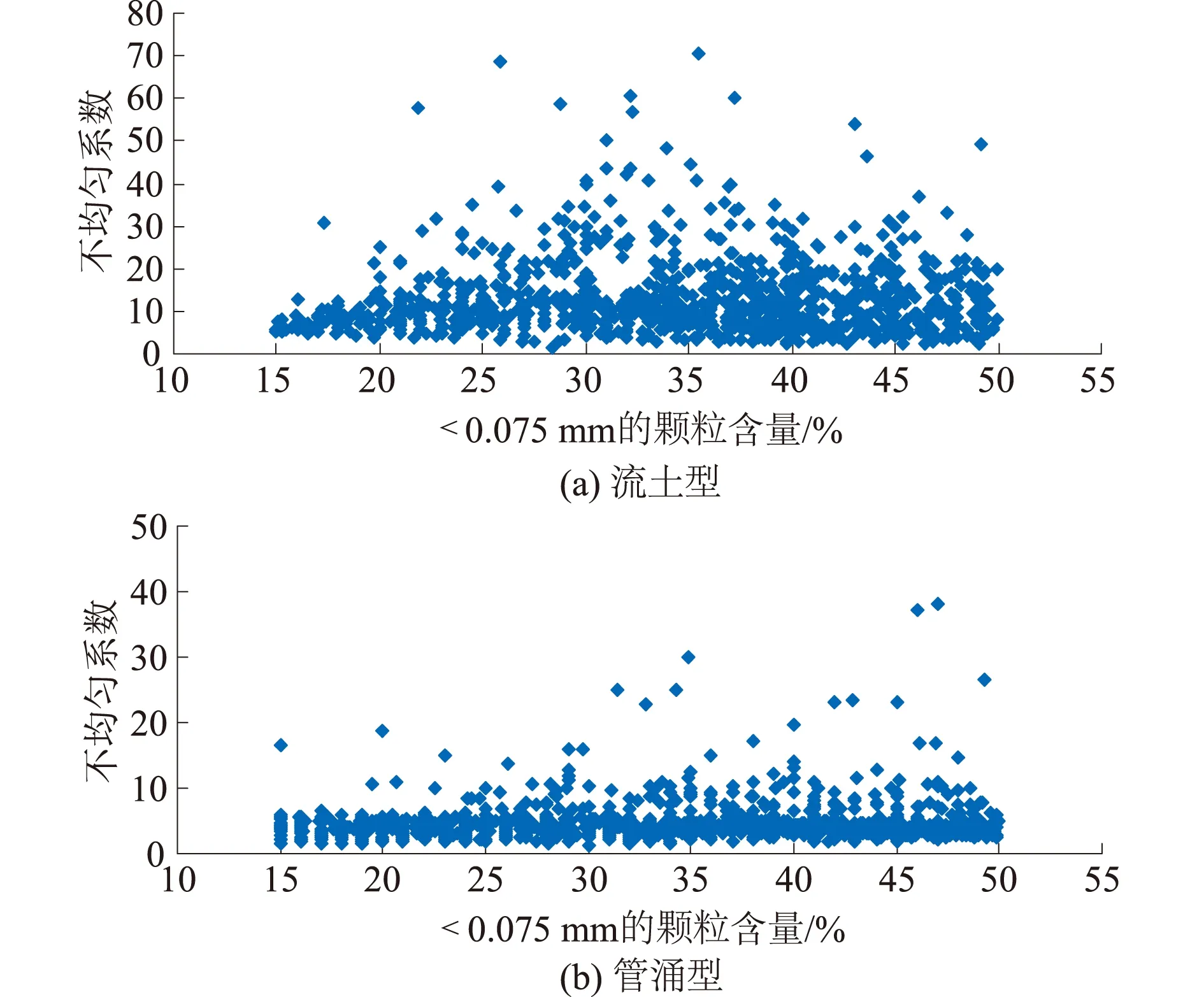
图3 尾粉砂不均匀系数与<0.075 mm颗粒含量散点图Fig.3 Scatter diagram of uniformity coefficient andsoil content with size less than 0.075 mm of tailing silt

通过对图2(a)与图2(b)、图3(a)与图3(b)叠加分析，结合室内渗透变形试验校验，得到了尾粉砂产生管涌的颗粒级配条件(见表2)。

表2 尾粉砂发生管涌的颗粒级配条件

室内实测试验发现，级配条件保持不变，当试样接近或超过最大干密度(采用标准振动击实法测定)时，部分试样发生管涌的临界水力梯度大于发生流土的临界水力梯度。表2得出的结论只适用于上游法尾矿堆积坝自然堆积形成的尾粉砂发生管涌的判定。

国内外鲜见有关尾矿的渗透变形判别方法的报道，而研究一般天然土与筑坝填料管涌的水力条件和几何条件的文献很多。前苏联的伊斯托美娜[8](Istomina，1957)提出了以土体的不均匀系数Cu判别土体的渗透变形类别，认为在自上而下的渗流作用下，当Cu≤10时为流土，Cu≥20时为管涌，10

一般来说，级配均匀的试样容易发生流土，而级配不均匀或级配间断的试样才容易发生管涌，表2中3种管涌条件的不均匀系数均小于10，即颗粒比较均匀，这与人们的认识不一致，造成这种认识的差异是尾矿的特殊性和仅用不均匀系数作为判据的缺陷所至。管涌产生的条件是[9]，管涌多发生在非黏性土中，其特征为：颗粒大小比值差别大，往往缺少某种粒径，磨圆度好，孔隙大而互相连通，细粒含量少，不能全部充满孔隙。颗粒多由相对密度较小的矿物构成，易随水流动，有较大和良好的渗透水流出路等。

尾粉砂是尾矿水砂混和液在沉积滩经有限的水力分选，自然堆积的松散体，由黏粒组、粉粒组和砂粒组构成，堆积体呈欠压密状态。虽然尾粉砂粒径分布区间窄，相对密度大，磨圆度差，但在特定的级配条件下，粗骨料砂粒组仍能形成有效的连通孔隙，使细粒料的黏粒和极细粉粒在一定的水力作用下能在连通孔隙通道中移动。表2中判据的3个要素恰好是限定尾粉砂在相对较小的粒组分布区内满足发生管涌的孔隙特征。显然，当尾粉砂中的细粒料的直径小于粗粒料形成的连通孔隙的直径时，在水力作用下，可产生管涌。

采用孔隙直径判别法[9]进行验证：当D0>d5时，管涌型；D0

按尾粉砂d5=0.005 4 mm、d20=0.033 1 mm计算孔隙率为0.359，0.391，0.438，0.453，0.469对应的D0值分别为0.007 5，0.008 2，0.009 1，0.009 5，0.009 8，均大于d5，按孔隙直径法判定管涌型。这表明前述的讨论分析是合理的。

2.2 临界水力梯度与孔隙之间的关系

为探讨尾粉砂孔隙特性与临界水力比降的关系，在武钢大冶白雉山尾矿库(铁矿)干滩采取了具有管涌特征的尾粉砂试样。将试样风干、拌匀，取代表性试样测定其相对密度与级配特征，依据表2判定试样是否属管涌型。

取经判定符合要求的试样测定其最大干密度与最小干密度，在最大干密度与最小干密度之间设定4～5个干密度值，使试样的孔隙率在0.35～0.55之间。按该密度值制备试样进行渗透变形试验，测定其发生管涌的临界水力比降。每个密度平行测2次，2次平行差小于10%时有效，取其平均值，2次平行差大于10%时重做。

渗透变形试验采用武汉勘察研究院有限公司自行研制的wkj-02多功能渗透变形试验仪，见图4。渗透容器由底座、试样管及导向管3部分通过3根长螺杆联结组合，试样管内径100 mm，高度200 mm，导向管内径120 mm。试验水头由带溢流口的升降水箱提供，并通过微型水泵为升降水箱循环供水。侧压水头可由侧压管量读，也可通过差压传感器由计算机监测记录。使用前对试验仪器进行了检测与标定，检测结果满足《变水头(常水头)渗透仪校验方法》(SL115—95)[10]对水力量测要求。

图4 wkj-02多功能渗透变形试验仪Fig.4 wkj-02 multifunctional seepage deformation tester

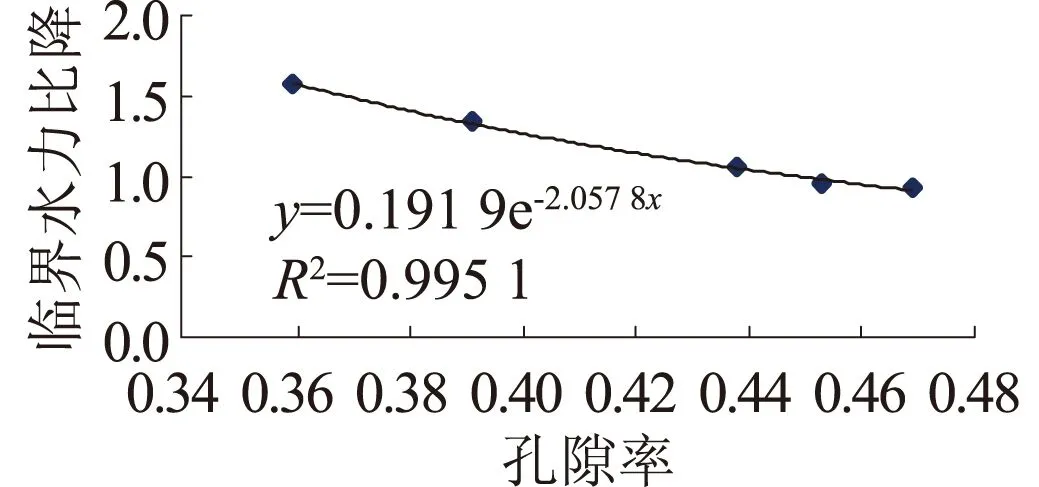
图5 临界水力比降与孔隙率关系曲线Fig.5 Relation curve of critical hydraulic gradient and porosity

试验时，首先按设计的干密度称取砂样，加入1%～2%脱气水拌匀，调整升降水箱水头，使水头与置于底座顶端的下透水板平齐，待底座充满水后关闭进水阀。在试样管内将砂样分层击实成形，在试样顶端放入导向环(外径与导向管内径相同，内径与试样管相同)，在导向环内充填中粗砂，将上透水板放在导向环上，盖好上盖，并通过上盖中心的活塞固定上透水板(孔径3～5 mm)。缓慢升高水箱，排除管路中的气体后，参照《土工试验规程》(SL237—1999)[11]中粗颗粒土的渗透及渗透变形试验方法的要求进行测试与资料整理。试验用水为脱气自来水，试验成果见表3和图5。

由图5可以得到尾粉砂在相对密度与级配特征保持不变时临界水力比降与孔隙率关系，即

(2)

2.3 临界水力梯度计算通式推导

尾粉砂是人工破碎堆积物，颗粒形状、堆积方式基本一致。由图1也可以看出，其孔隙率(孔隙比)的大小与其相对密度没有关系，且不同矿种的尾粉砂的孔隙率波动范围基本相同。由此可推断不同矿种的尾粉砂的孔隙特性对临界水力梯度的影响因子也应基本相同。因此，通过特定的尾粉砂样品测得的临界水力梯度与孔隙大小之间的变化规律具有一般性，即式(2)所表述的函数变化规律适用于所有尾粉砂。

播音主持的语言运作能力，包括语言使用是否得体、言辞内容是否精准、语句是否优美等，这都会影响节目的播出质量，而且在整个节目串联中都需要使用到语言，这关系节目整体的播出效果，影响收视收听率。由此可见，播音主持语言功力的重要作用。

尾粉砂临界水力梯度的大小取决于其孔隙特性、相对密度和颗粒级配特征。由式(1)可知，颗粒浮重度与临界水力梯度大小成正比例关系，表征颗粒级配特征的d5/d20比值与临界水力梯度亦成正比例关系。式(2)表示的是在相对密度与d5/d20比值保持定值时，临界水力梯度与孔隙率之间的关系，只有在式(2)中引入相对密度与d5/d20比值的校正系数才能得到通用计算式。

尾粉砂的相对密度因矿种的差异，基本在2.60～3.50之间波动，对临界水力梯度值有很大的影响，假定2种不同相对密度的管涌型尾粉砂的孔隙率完全一样，令其孔隙对临界水力梯度的影响因子为N；第1种相对密度为Gs1、临界水力梯度为Jcr1；第2种相对密度为Gs2、临界水力梯度为Jcr2。

则有：

(3)

(4)

式(3)与式(4)相除并整理得

(5)

根据式(1)也可推导出与式(5)相同的结论。将式(2)及对应的相对密度值代入式(5)得

(6)

管涌型尾粉砂的颗粒形状特征与级配特征基本一致，发生管涌时，均是黏粒与极细粉粒在砂粒组的孔隙中移动，黏粒与极细粉粒相对含量的大小对尾粉砂的临界水力梯度值有一定的影响。在《水利水电工程地质勘察规范》(GB50287—2008)中，这种影响因素用d5/d20值表示，且临界水力梯度值与d5/d20值成正比。

假定2种管涌型尾粉砂的相对密度、孔隙率完全一样，令其孔隙对临界水力梯度的影响因子为N1，相对密度影响因子为N2，第1种d5/d20值x1、临界水力比降为Jcr1；第二种d5/d20值x2、临界水力比降为Jcr2。则有：

(7)

(8)

(9)

即

(10)

表3中x1(d5/d20)值为0.163,将式(6)代入式(10)得

(11)

式(11)即是采用尾粉砂的物性指标计算尾粉砂临界水力梯度的通用计算公式。

3 试验检验

为检验计算式计算结果的可靠性，分别选用了从湖北黄石金铜矿业冯家山尾矿库(干滩采样)、浙江绍兴平水铜矿尾矿坝(钻孔留样)和武钢大冶白雉山尾矿库(开挖辐射井9 m处留样)采取的尾粉砂样品，在试验室风干碾散，用相对密度瓶法测定其相对密度。将每组样品分别过0.075 mm筛，分成筛上与筛下2部分。按试验设计的比例称取相应的筛上与筛下尾砂拌匀，制成9个试验样品。选用密度计法分别测定9个试验样品的颗粒级配特征参数。

按设计的控制干密度从试验样品中称取砂样，加入砂样质量1%～2%的水拌匀，在渗透变形试验仪试样管中分层击实成型。在试样的出水端放置多孔(孔径3～5 mm)透水板并锁定。按渗透变形试验的要求，对试样进行饱和与分级施加水头(试验用水为脱气自来水)，试样破坏时结束试验，试验结果见表4。

由表4可知，实测值与计算值基本吻合，实测临界水力梯度平均值略大于采用式(11)计算的平均值，计算结果偏于安全。

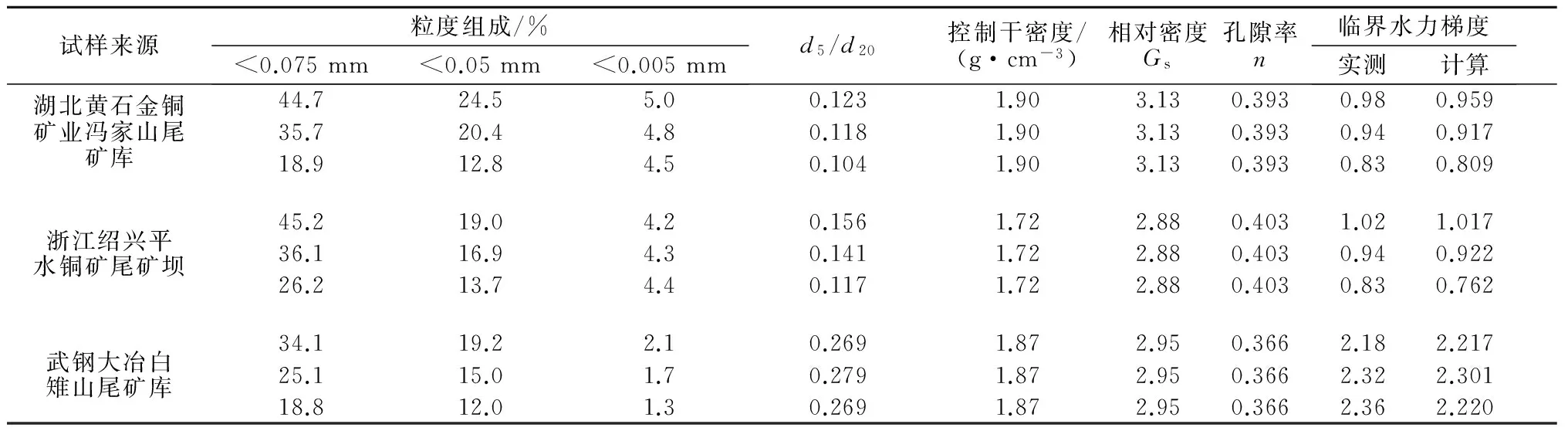
表4 室内检验测试成果汇总

表4中的实测与计算的临界水力梯度是指尾粉砂发生管涌的临界值，当其发流土的临界水力梯度值小于发生管涌的临界值时，发生渗透变形的破坏类型应为流土，取流土的临界水力梯度值为其临界水力梯度。流土的临界水力梯度值可按《水利水电工程地质勘察规范》(GB50287—2008)推荐的公式进行计算。

4 结 语

通过调研多座尾矿坝中尾粉砂的颗粒级配，统计出尾粉砂发生管涌的颗粒级配条件。统计结果可用于上游法尾矿堆积坝中尾粉砂发生渗透变形类别的估判。

在分析尾粉砂颗粒形态特征、颗粒级配特征、孔隙特征与临界水力梯度之间的关系的基础上，用特定的尾粉砂试样测定其发生管涌的临界水力梯度与孔隙率(比)之间的函数关系，利用颗粒相对密度、d5/d20比值分别与临界水力梯度呈正比例关系导出尾粉砂发生管涌的临界水力梯度的计算通式。该计算通式的计算结果与室内实测结果基本吻合，可用来估算尾粉砂发生管涌的临界水力梯度值，估算值略偏于安全。

[1] 唐大雄, 孙愫文. 工程岩土学[M]. 北京: 地质出版社, 1987.

[2] 李广信, 周晓杰. 堤基管涌发生发展过程的试验模拟[J]. 水利水电科技进展, 2005, 25(6): 21-24.

[3] 魏 勇, 潘红洁, 郭利杰. 尾矿坝坝基管涌砂槽模型试验研究[J]. 金属矿山, 2011, (8): 140- 142.

[4] 丁树云, 蔡正银. 土石坝渗流研究综述[J]. 人民长江, 2008, 39(2): 33- 36.

[5] 朱崇辉,刘俊民,王增红. 粗粒土的颗粒级配对渗透系数的影响规律研究[J]. 人民黄河, 2005, 27(12): 79-81.

[6] 朱崇辉, 王增红, 刘俊民. 粗粒土的渗透破坏坡降与颗粒级配的关系研究[J]. 中国农村水利水电, 2006, (3): 72- 74.

[7] 朱崇辉, 刘俊民, 王增红. 无黏性粗粒土的渗透试验研究[J]. 人民长江. 2005, (11): 53-55.[8] ISTOMINA V S. 土的渗流稳定性[M]. [s. 1.]: [S. n.], 1957.

[9] 《工程地质手册》编委会. 工程地质手册(第四版)[M]. 北京: 中国建筑工业出版社, 2007.

[10]SL115—95, 变水头(常水头)渗透仪校验方法[S]. 北京: 中国水利水电出版社, 1995.

[11]SL237—1999, 土工试验规程[S].北京: 中国水利水电出版社, 1999.

(编辑：黄 玲)

Discussion on the Method for Calculating Critical Hydraulic Gradientof Piping-typed Tailing Silt

CHEN Ding-an, YU Chen-xiang

(Wuhan Surveying & Geotechnical Research Institute Co., Ltd. of MCC, Wuhan 430080,China)

The critical hydraulic gradient of tailing silt is greater than that of conventional sand soil， which is determined by the tailing silt’s structure characteristic，and the calculated critical hydraulic gradient of piping-typed tailing silt by conventional formula is far less than the measured values. Therefore, the conventional calculation methodcan not be applied to tailing silt. Through collecting large amount of physical indexes and particles characteristic indexes of the tailing silt and comparing the grain size distribution characteristics of flowing soil-typed tailing silt with that of piping-typed tailing silt, we deduced the tailing silt’s grain size distribution conditions in which piping occurred. Afterwards, based on the analysis of the correlations between critical hydraulic gradient and the particle morphology or the grain size distribution, pore characteristics, the function relationship between the critical hydraulic gradient and the porosity (void ratio) of particular tailing silt was measured when the piping generates, and then a generalized computing equation of critical hydraulic gradient was exported. Finally, the reliability of the general formula calculation results is properly verified by laboratory test, and the results show that the measured value is basically in agreement with the calculated value. Therefore, this calculation formula can be used to estimate the critical hydraulic gradient of piping-typed tailing silt, and the estimation result is on the safe side.

tailing silt；piping；critical hydraulic gradient；grain size distribution；porosity

2014-08-02；

2014-09-03

陈定安(1964-)，男，湖北武汉人，高级工程师，主要从事岩土工程测试、工程咨询与岩土新技术研发的工作，(电话)13971532251(电子信箱)564285549@qq.com。

10.11988/ckyyb.20140642

2016,33(01):101-105，110

TU502

A

1001-5485(2016)01-0101-05