基于小波分解和支持向量机的大坝位移监控模型

姜振翔，徐镇凯，魏博文

(南昌大学 建筑工程学院，南昌 330031)



基于小波分解和支持向量机的大坝位移监控模型

姜振翔，徐镇凯，魏博文

(南昌大学 建筑工程学院，南昌 330031)

常规大坝安全监控统计模型未能分别针对监测序列值内系统信号和随机信号特点进行模拟，故预报精度存在一定的提升空间。基于小波分解技术，利用监测序列值信号频率特征分离出系统信号与随机信号，并结合逐步回归与支持向量机(SVM)对不同信号的处理优势，在引入网格寻优与交叉验证确定SVM敏感参数的基础上，提出了一种基于多元统计结合小波分解和支持向量机的大坝位移监控模型，同时编制了其相应的计算程序。工程算例表明，该模型较常规模型能够同时考虑监测序列中的系统信号和随机信号，并且具有较强的模型寻优能力和更高的预报精度，从而验证了所建模型的有效性，该方法亦可推广应用于高边坡及大坝其他预警指标的监控。

大坝位移；小波分解；参数寻优；支持向量机；监控模型

1 研究背景

建立有效的安全监控模型是保障大坝运行安全的关键因素之一[1]，而现行常规统计模型难以区分原始监测数据中同时存在变化相对平稳的系统信号与变化相对剧烈的随机信号[2]。故采用单一的线性方程[3-4]难以表达出随机信号的不规则变化，导致欠拟合[5]；而采用单一的机器学习[6- 7]算法建模时，则会忽视水位、温度、时效等因素与系统信号间的线性关系，导致模型的泛化能力差[8]，从而影响预报精度。

小波[9]分解是一种重要的频率分析方法，能够根据系统信号与随机信号频率的变化特征实现二者的分离。经小波分解后得到的系统信号，其频率较低，平稳性较高，适合采用线性方程表达[10]；而对于随机信号，其频率较高，具有一定的非线性特征，故可采用非线性方程[11]进行模拟。因此，本文首先利用小波分解大坝位移监测原始信号，提出了线性模型与非线性模型叠合的监控模型，并结合逐步回归与支持向量机[12](SVM)的算法优势，分别对其中的系统信号与随机信号进行训练，采用网格搜索算法确定SVM敏感参数，最后得到了基于多元统计结合小波分解和支持向量机的大坝位移监控模型。

2 基于监测信号小波分解的大坝位移监控模型

2.1 位移监测信号的预分离

通常认为，传感器采集到的信号中包含了系统信号与随机信号，其中系统信号具有明显的趋势性和规律性，频率较低；而随机信号的变化特点较为复杂，往往表现出非线性，频率较高。大坝位移监测信号同样具有这些特征，通常认为大坝位移由水压分量δH、温度分量δT以及时效分量δθ等分量组成，分别受水深H、温度T以及时效θ等因子的影响。由文献[1]可知，在对坝体、坝基模型进行适当简化后可导出δH与H和δT与T间的线性表达式，其变化规律明显，故可认为监测信号中的系统信号体现了这一线性关系。但由于简化模型、简化计算等因素的存在，可知各分量与各因子之间也存在部分非线性关系，而该关系则通过随机信号表现。因此，在建立大坝位移监控模型前，有必要先从原始监测资料中分离出系统信号与随机信号。

小波分解能够利用系统信号与随机信号的频率特征，通过用一系列函数去逼近原始信号频率，进而实现对两者的分离。大坝位移原始监测信号δ(H,T,θ)在分解尺度J下的分解表达式为

(1)

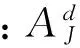
(2)

(3)

式中：φJ，k(x)为尺度函数；cJ,k为尺度展开系数；ψJ，k(x)为小波函数；dJ,k为小波展开系数；k为分解层数；Z为整数集。

2.2 叠合系统与随机信号的大坝位移监控模型

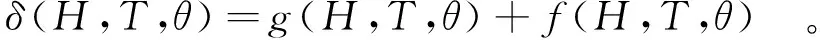
(4)

上式中，由于随机信号的变化特征，其非线性模型通常难以用显示方程表达。对于运行多年的大坝，坝体内部已达到稳定温度场，同时时效位移的变化也趋于稳定，由文献[1]选择回归因子后，监控模型可展开为

(5)

式中：am，bq，b1r，b2r，c1和c2为回归系数，对于重力坝m可取3，拱坝m可取4或5；当λ=0时，表示选用多周期的谐波作为因子，l为周期，l=1为年周期，l=2为半年周期，t为监测值至始测值累计天数，当λ=1时，表示坝内有足够数量温度计，选用各温度计的测值作为温度分量的因子，Tq为第q支温度计的变温值，p为温度计支数；θ=t/100。

对施工期及蓄水初期的大坝建立位移监控模型时应对式(5)进行修正，由于其时效位移变化较大，故应结合文献[1]，根据实测位移变化趋势采用适当的时效位移数学模型作为回归因子。

3 组合模型中两相信号的处理方法及数值流程

3.1 系统与随机信号的处理方法

大坝位移原始监测资料经分解后，可通过不同的数据训练方法得出相应的模型。在训练系统信号、建立线性模型时，可采用逐步回归方法，与一般的多元回归方法相比，逐步回归优点在于其剩余标准差较小，方程的稳定性较好，能够保证方程中所有回归因子都具有显著性。采用逐步回归分析时，按对回归因子显著程度的大小，将其逐个引入回归方程，同时，已被引入回归方程的回归因子也可能会因为失去重要性而被剔除。通过在训练样本时不断引进并检验、剔除不显著变量，最终确定回归方程系数。

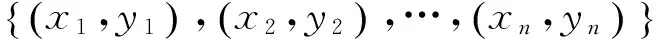
(6)

式中：wT为权重向量；b为常数。设置核函数参数g，采用RBF核函数，即

(7)

并设置惩罚系数C、松弛系数ξ，经风险最小化原理有

(8)

以及KKT互补条件[12]求解后，可得到拟合函数为

(9)

式中ai为拉格朗日乘子。

在利用SVM建模时，其拟合精度很大程度上取决于惩罚系数C值和核函数参数g值。在此采用网格搜索与交叉验证的方式对C和g进行优选，其方法为：①设置C和g的搜索范围以及步长；②将训练样本随机分为M组，将每组数据分别做一次训练集，其余的验证集进行测试，得到M个模型；③对于任一模型，在C和g的搜索范围内，找到使得各验证集均方误差(MSE)的均值最低的C和g；④将该过程重复M次，最终选择MSE均值最低的模型所对应的C和g作为最佳参数。

3.2 两相信号叠合的数值流程

结合上述建模方法，本文提出利用逐步回归与支持向量机算法建立大坝位移监控组合模型的一般步骤为：

(1) 获取大坝位移监控原始数据。

(2) 由式(1)至式(3)，小波分解原始数据，得到系统信号与随机信号。

(3) 根据式(5)计算回归因子，采用逐步回归训练系统信号得到线性模型；回归因子归一化后根据式(6)至式(9)，采用SVM训练随机信号。

(4) 设置惩罚系数C和核函数参数g的搜索范围。

(5) 通过网格搜索与交叉验证，找到最佳C和g，确定SVM模型。

(6) 根据式(4)，将线性模型与SVM模型叠加。

根据上述建模步骤，本文给出组合模型建模流程如图1所示。

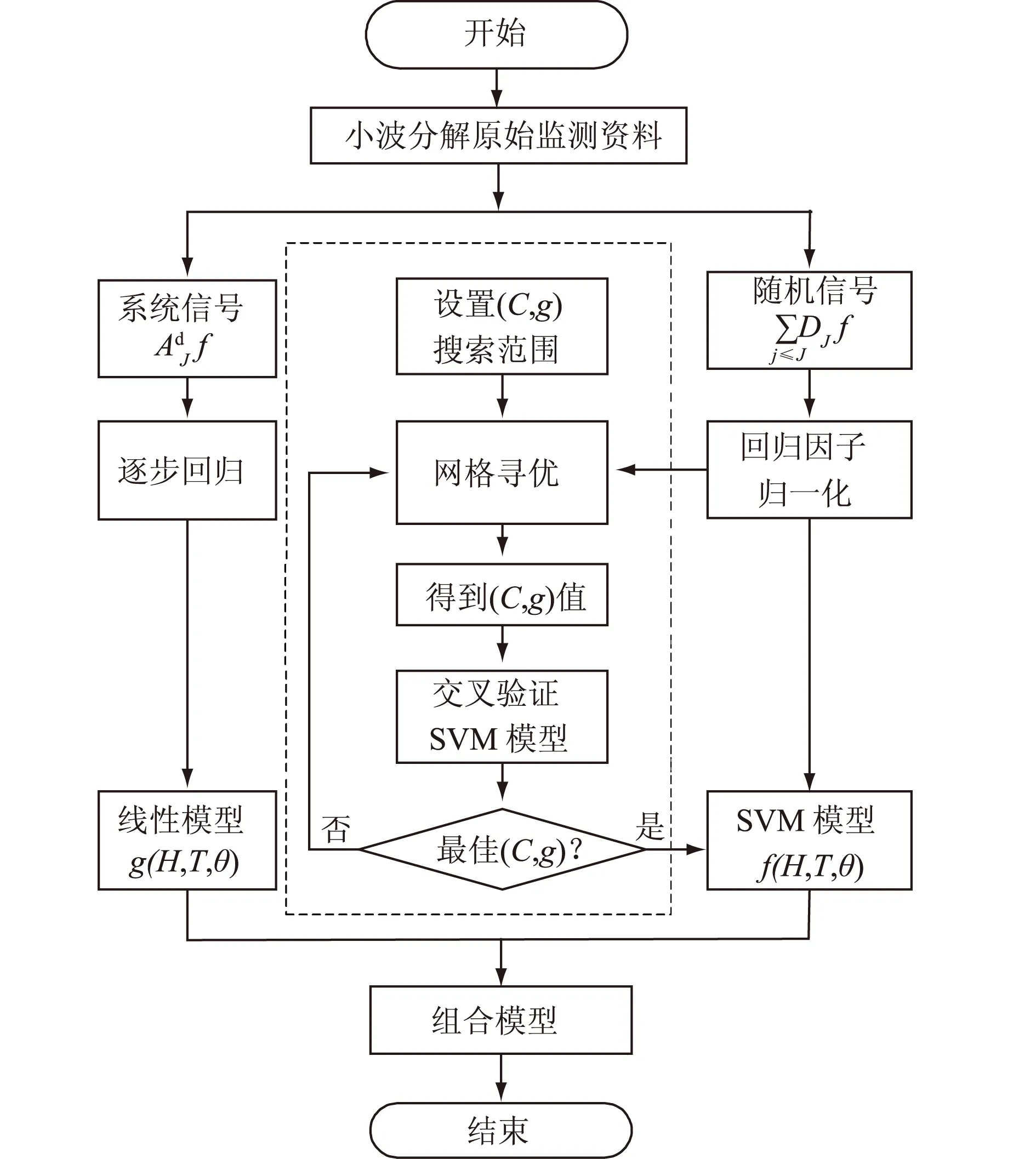
图1 逐步回归-支持向量机模型建模流程Fig.1 Flow chart of constructing stepwise regression-SVM model

4 工程实例

某混凝土重力坝的最大坝高113.0 m，坝顶全长308.5 m，坝顶高程为179.0 m。水库正常蓄水位173 m，调节库容11.22亿m3，校核洪水位177.80 m，总库容20.35亿m3。该坝已服役多年，具有较为完善的监测系统,并积累了多年监测序列。其中引张线监测设备设在坝顶179.00 m高程处，自坝左到坝右依次布置12个测点。本文利用某引张线监测点监测值，通过小波分解，将分离出的系统信号与随机信号分别利用逐步回归、支持向量机建模，从而建立了大坝位移监测的组合模型。

4.1 样本的选取与小波变换

本文选取2008年6月1日至2008年11月28日的监测数据进行分析，由于受环境、仪器自身精度等复杂因素的影响，部分测值存在明显异常，不应纳入建模样本。在剔除了明显的异常测值后，共得到165组监测数据，采用Matlab软件中的小波工具箱，选择工程中常用的Db4小波[13]对位移资料进行了3层分解。测点原始测值、经分解后得到的系统信号、随机信号如图2所示，同时绘出坝前水位变化过程线。

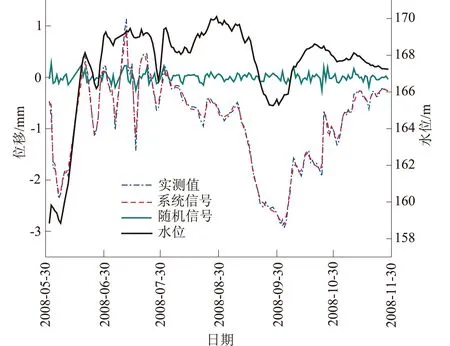
图2 位移实测值、系统信号、随机信号以及坝前水位Fig.2 Measured displacement, systematic signal,random signal and water level before dam obtained from monitoring points

由图2可知，从总体上看大坝位移实测值与水位变化具有一定的线性关系，而经过Db4小波分解得到的系统信号与位移实测值的变化趋势具有一致性，并且较原始信号平滑，有利于使用逐步回归方法进行线性拟合;而随机信号的分布则具有较高的离散性，表明其变化与水位等因素间存在一定的非线性关系，故更适合于利用SVM建模。

4.2 大坝位移监测组合模型的建立

根据3.2节建模流程，选取分解后前157组监测数据作为训练样本，后8组作为测试样本。鉴于该坝为运行多年的混凝土重力坝，故式(5)中的m值可取3，将其作为水位的回归因子，并采用谐波因子作为温度的回归因子、观测累计天数的对数函数作为时效的回归因子。将系统信号作为因变量，通过逐步回归方法建立了线性回归方程；同时将回归因子归一化，选择径向基核函数，以随机信号作为因变量，建立SVM模型。在选择SVM参数时，引入网格搜索算法，设置惩罚系数C的搜索范围为[2-5,25]，核函数参数g的搜索范围为[2-5,25]，搜索步长取20.8，并将训练样本分为5个部分进行交叉验证。由于搜索范围较大，故采用log2g和log2C作为横坐标，得到网格寻优过程如图3所示。从图中可知，在相等的MSE下存在多组C和g组合，故MSE具有等高线的性质。由于随机信号值偏小，故MSE在较大处等高线稀疏，而在MSE较小处等高线密集。当在最低MSE为3×10-4处寻找到多组C和g后，一般选择最小的C值作为模型最佳参数，以提高SVM的泛化能力，因此选择最佳C值为0.003 9，最佳g值为256。

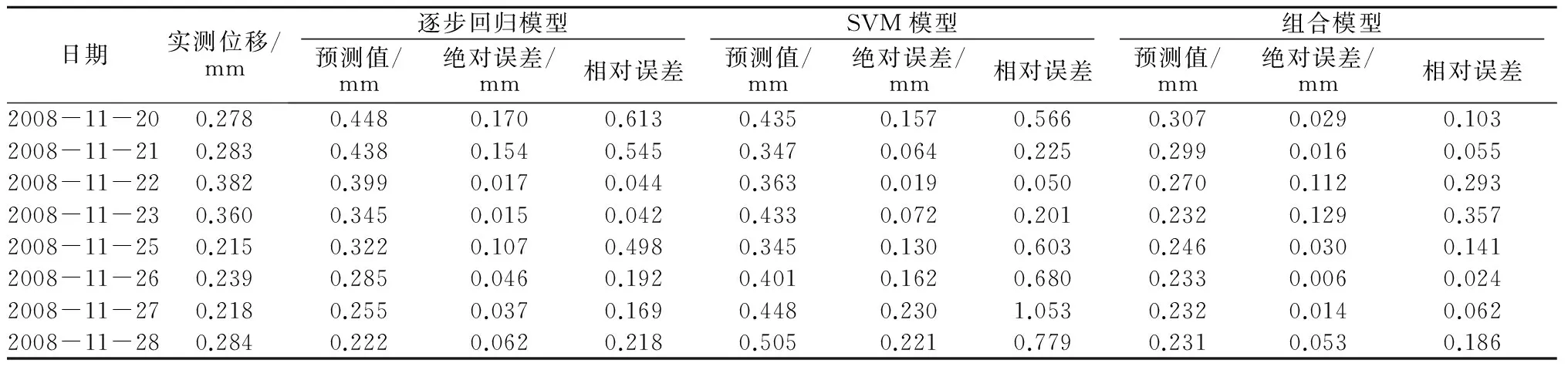
表1 测试样本下各模型预测结果比较

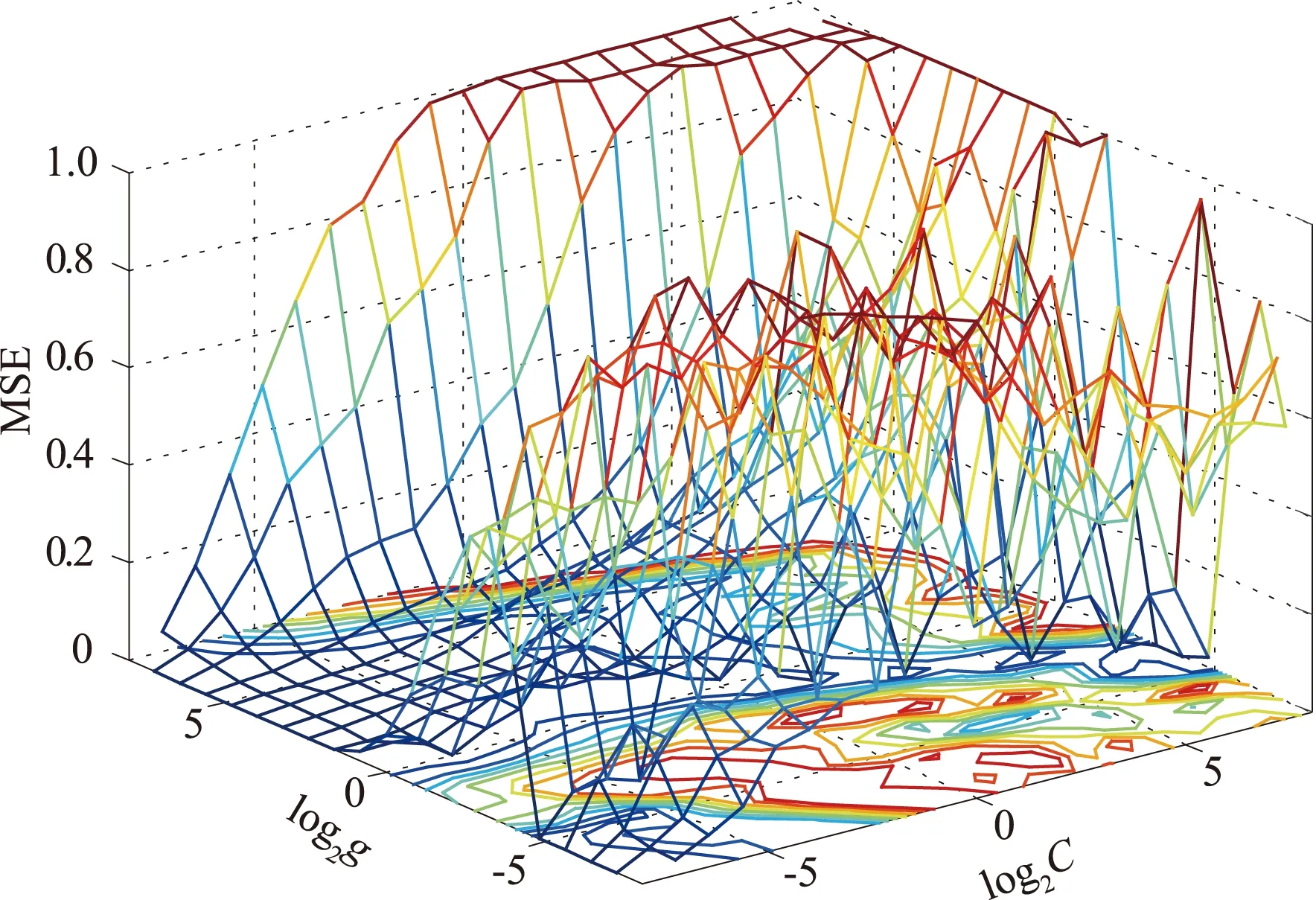
图3 网格寻优过程Fig.3 Optimizing process of grid search

4.3 模型精度分析

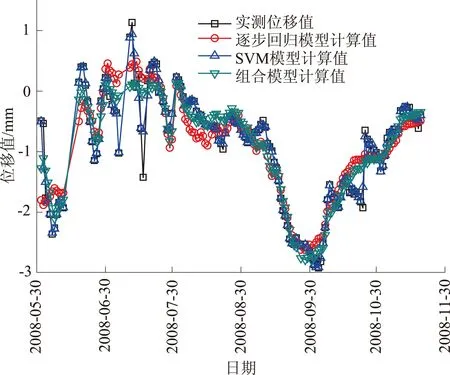
图4 各监测模型的计算值Fig.4 Calculated values of various models

模型建立后，利用其计算出在157组训练样本下的拟合值以及在8组测试样本下的预报值，以考察模型的有效性。为体现组合模型的精度优势，本文还建立了未经小波变换、直接利用原始监测信号建立的逐步回归模型、SVM模型(采用网格寻优算法找到最佳C值为9.18，g值为84.44)，各模型的拟合值与预报值如图4所示，同时列出各模型的预报值以及误差如表1所示。

由图4可知，各模型的拟合值以及预报值变化趋势均与实际观测值相近，可用于预报分析，而从表1可得，在测试样本下，组合模型的误差指标总体上要低于逐步回归模型与SVM模型。为了更清楚地表现各模型的预报精度，本文统计了3种模型拟合值以及预报值的MSE、平均绝对百分误差(MAPE)等误差指标，其中MSE可以反映计算值相对实测值的整体变化程度，而MAPE可以从衡量计算值与实测值误差的整体水平，各模型在不同阶段的误差指标如表2所示。

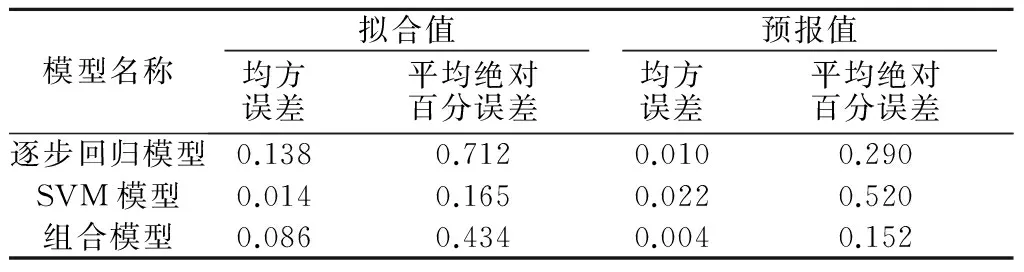
表2 各监测模型误差指标

由表2可知，对于在训练样本下得到的拟合值，SVM模型的优势突出，这体现了SVM良好的学习能力，而逐步回归模型的误差较大，这主要是由于监测数据中系统信号与随机信号共存，其中随机信号的变化具有非线性特征，故在线性拟合的过程中，对线性方程系数进行估计时，容易产生较大偏差，从而对模型精度造成影响。但对于预报值，组合模型的误差指标均优于其他两类模型，其中SVM模型的误差指标较高，原因在于大坝位移与水位、温度、时效等变量间存在一定的线性关系，当采用SVM进行非线性预报时，模型的泛化能力受到影响。而组合模型的误差又低于逐步回归模型，这是因为大坝位移与上述变量间还存在部分非线性关系，故采用组合模型中的SVM能够对其进行较好模拟，有利于精度的提高。

5 结 语

(1) 小波分解技术能够将坝体位移监测资料中的系统信号和随机信号有效分离，本文在各信号变化特征的基础上，提出了线性模型与非线性模型叠合的大坝位移监控模型。

(2) 采用逐步回归与SVM算法建立的大坝位移监控模型，能够克服常规统计模型的不足，工程算例表明，所建模型的预报精度明显提升，从而证明了所建模型的有效性，可推广应用于高边坡及大坝其他预警指标的监控。

(3) SVM在模拟大坝位移信号时表现出较强的学习能力，采用网格搜索算法优化SVM参数，可以避免试算的低效率和盲目性，但在寻优过程中，如何根据随机信号特点设置并逐步缩小C和g搜索范围，以提高建模速度，还可作进一步的研究。

[1] 吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003.

[2] 汪树玉, 刘国华, 杜王盖. 大坝观测数据序列中的混沌现象[J]. 水利学报, 1999, (7): 22-26.

[3] STOJANOVIC B, MILIVOJEVIC M, IVANOVIC M,etal. Adaptive System for Dam Behavior Modeling Based on Linear Regression and Genetic Algorithms[J]. Advances in Engineering Software, 2013, 65(10): 182-190.

[4] 许 昌, 岳东杰, 董育烦, 等. 基于主成分和半参数的大坝变形监测回归模型[J]. 岩土力学, 2011, 32(12): 3738-3742.

[5] 李子阳, 郭 丽, 顾冲时. 大坝监测资料的时变Kalman预测模型[J]. 武汉大学学报(信息科学版), 2010, 35(8): 991-995.

[6] 王雪红,刘晓青,陶海龙,等.优化BP神经网络的位移预测模型[J].水利水运工程学报,2014,(2):38-42.

[7] 朱凤林, 韩 卫. Matlab 仿真平台下大坝位移BP神经网络模型研究[J]. 长江科学院院报, 2013, 30(1): 99-101.

[8] 缪新颖, 褚金奎, 杜小文. LM-BP神经网络在大坝变形预测中的应用[J]. 计算机工程与应用, 2011, 47(1): 220-222.

[9] BURRUS C S , GOPINATH R A , GUO H. Introduction to Wavelets and Wavelet Transforms: A Primer[M]. Englewood Cliffs, United States: Prentice Hall, 1997.

[10]李端有, 周元春, 甘孝青. 混凝土拱坝多测点确定性位移监控模型研究[J]. 水利学报, 2011, 42(8): 981-985，994.

[11]李 波, 顾冲时, 李智录, 等. 基于偏最小二乘回归和最小二乘支持向量机的大坝渗流监控模型[J]. 水利学报, 2008, 39(12): 1390-1394，1400.

[12]丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 2-9.

[13]徐洪钟, 吴中如, 李雪红, 等. 基于小波分析的大坝变形观测数据的趋势分量提取[J]. 武汉大学学报(工学版), 2003, 36(6): 5-8.

(编辑：曾小汉)

A Monitoring Model of Dam Displacement Based onWavelet Decomposition and Support Vector Machine

JIANG Zhen-xiang, XU Zhen-kai, WEI Bo-wen

(College of Civil Engineering and Architecture，Nanchang University，Nanchang 330031,China)

The systematic signal and random signal in the monitoring sequence are difficult to distinguish in the conventional monitoring models of the dam, thus the forecasting accuracy of the conventional model can be promoted. In this paper, we separate the systematic signal from random signal by their frequency features based on wavelet decomposition. According to the advantages of managing signals of stepwise regression and Support Vector Machine(SVM), in association with grid search and cross validation methods for determining the sensitive parameters of SVM, we present a monitoring model of dam displacement based on multivariate statistical combined with wavelet decomposition and support vector machine. Then the calculating procedures are compiled. The engineering examples indicate that both the systematic signal and random signal can be separated effectively in the composite model, with high forecasting accuracy and good optimization ability. Finally， the composite model is effective and the method can be applied to high slope monitoring and other warning indicators of dam projects.

dam displacement; wavelet decomposition; parameter optimization; support vector machine; monitoring model

2014-08-09 ；

2014-09-02

国家自然科学基金项目(51569014，51409139)

姜振翔(1989-)，男，江西南昌人，硕士研究生，从事水工结构安全监控及风险分析，(电话)15071264157(电子信箱)jiangzhenxiang89@163.com。

魏博文(1981-)，男，江西彭泽人，讲师，博士，从事水工结构数值分析及安全监控研究，(电话)13767428612(电子信箱)bwweincu@126.com。

10.11988/ckyyb.20140690

2016,33(01):43-47

TV698.1

A

1001-5485(2016)01-0043-05