基于率定量化标准系数的SPA年径流预测

李深奇，肖景西，覃光华, 1b，张泽慧

(1.四川大学 a.水利水电学院；b.水力学与山区河流开发保护国家重点实验室，成都 610065;2.达州市水文水资源勘测局, 四川 达州 635000)



基于率定量化标准系数的SPA年径流预测

李深奇1a，肖景西2，覃光华1a, 1b，张泽慧1a

(1.四川大学 a.水利水电学院；b.水力学与山区河流开发保护国家重点实验室，成都 610065;2.达州市水文水资源勘测局, 四川 达州 635000)

针对集对分析(set pair analysis,SPA)在径流预测中径流集合量化标准仅根据主观经验确定的问题，提出了率定量化标准系数的SPA年径流预测模型，即首先对量化标准系数进行率定，再用SPA模型对径流进行预测。将该模型应用于长江宜昌站，并与经验标准预测结果进行对比。结果表明，率定量化标准后的预测结果能更好、更准确地反映原序列的变化，精度更高。

率定量化标准系数；集对分析；年径流；预测模型; 经验标准预测

1 研究背景

集对分析(set pair analysis，SPA)是我国学者赵克勤1989年提出的一种利用联系数统一处理模糊、随机、中介和信息不完全所致的不确定性的系统理论和方法[1]。目前，集对分析在水文水资源领域的评价[2-3]、计算[4]等方面应用较多，在预测方面应用较少。冯利华等[5]将集对分析应用于水资源变化趋势的定性预测上，刘冀等[6]将参数优化后的集对分析应用于月径流预测，王红芳等[7]将集对分析应用于长江寸滩站年径流定量预测上，并将这些分析结果与模糊优选预测结果进行了对比，结果表明集对分析法具有计算简单、关系结构清晰、预测精度较高的特点。在以往采用集对方法进行径流预测时，量化径流集对中集合的标准仅根据研究者主观经验确定，不同的研究者量化标准不同，从而将会影响各个集合的同、异、反状态，进而对联系度产生影响，最终可能使预测结果不同。为了使量化集合的标准具有客观性，本文提出了率定量化标准系数的集对分析预测模型，并以长江宜昌站为例对模型进行了验证分析，将研究结果与经验标准预测结果进行了对比，结果表明，率定量化标准系数后的预测精度更高。

2 基于率定量化标准系数的SPA年径流预测模型

2.1 年径流预测的SPA原理

SPA是一种新的不确定性分析途径[1]，其基础是集对，所谓“集对”是指有一定联系的2个集合构成的对子，其中一个集合用A表示，另一个集合用B表示，则集对表示为H(A，B)。年径流预测的SPA就是要对径流集对H(A，B)中的集合A和B做同一性、差异性、对立性分析，即把集合A和B的特性作为一个确定不确定性系统进行处理，它们之间相互联系、相互影响、相互制约，用联系度表达式来描述，即

(1)

式中：N为径流集合元素的总数；S为径流集合中处于同一状态元素的个数；F为径流集合中处于差异状态元素的个数；i为差异性系数，因具体情况在(-1,1)区间取值，或者作为差异性标识符号；P为径流集合中处于对立状态元素的个数；j为对立性标识系数，在计算中j≡-1，或者作为对立性标识符号。令a=S/N，b=F/N，c=P/N，则式(1)简化为

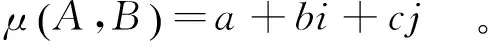
(2)

式中：a+b+c=1。a表示两径流集合的同一性程度，称为同一度；b表示两径流集合的差异性程度，称为差异度；c表示两径流集合的对立性程度，称为对立度。我们可以通过计算联系度的大小来确定两径流集合的相似性，进而对年径流进行预测。

2.2 基于率定量化标准的集对分析集合构造

率定量化标准系数的SPA预测模型的理念是以过去的径流状态直接预测未来的径流状态，即预测途径中的直接途径[8]。已知时间序列xt(t=p+1,p+2,…,n+1)与前p个相邻历史值xt-p，xt-p+1，…,xt-1存在相依性；将时间序列滑动生成容量为p的集合，分别记为A1，A2，…,An-p，这里称为历史集合；每个历史集合Ak(k=1,2，…，n-p)，对应着xk+p，称xk+p为后续值[9-10]。要对某一后续值进行预测，需构造其当前集合B=(xn-p+1，xn-p+2，…,xn)，然后在历史集合A1，A2，…，An-p中寻找与B最相似的集合Am，Am的后续值xm+p即作为xn+1的预测值。历史集合及当前集合见表1。

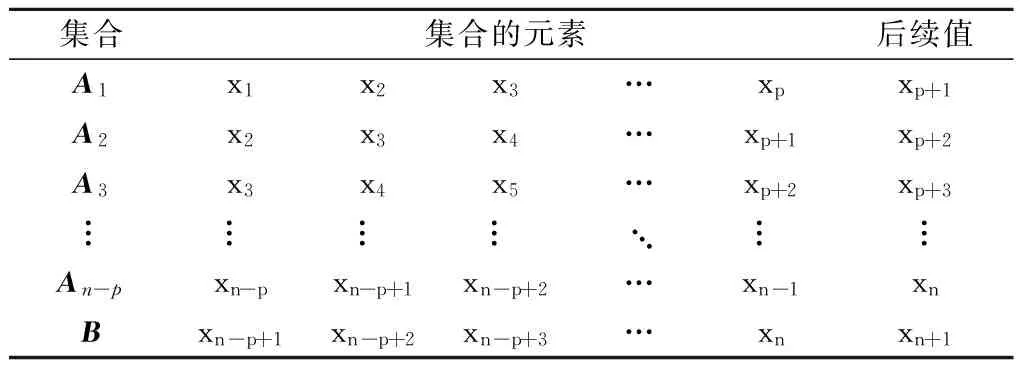
表1 历史集合Ak及当前集合B

可以看出预测的关键在于如何在历史集合中确定B的相似集合。而相似性选择的关键之一就是如何将集合进行合理的量化。为避免人为主观性，本文引入量化标准系数，首先对量化标准系数进行率定，然后分别对各历史集合与当前集合作同一性、差异性、对立性分析，计算出各集对的联系度uAk-B，最后通过联系度最大原则确定出B的相似集合。

2.3 量化标准系数的率定

(1) 已知年径流序列x1，x2,…，xn，如表1构造历史集合A1，A2，…，An-p和当前集合B及其对应的后续值xp+1，xp+2,…，xn,xn+1。考虑到年径流序列的弱相依性，p值一般选取4—6为宜。

(3) 将量化后的当前集合B与前n-p个历史Ak集合逐一进行对比，统计符号相同的个数记为S(同一性)，符号差一级的记为F(差异性)，符号差2级的个数记为P(对立性)，得到各个集对的联系度。

(4) 对i和j取值，计算集合Ak与B集合的联系数，最大的联系数对应的集合的后续值或者后续值的加权平均值作为预测值。

(5) 计算预测值与实测值的平均相对误差。

(6) 不断调整各集合量化标准系数，重复步骤(2)—(5)求出不同标准下的平均相对误差，认为平均相对误差最小时对应的量化标准系数为率定后的量化标准系数。

用上述率定后的量化标准系数按步骤(1)—(5)应用于检验阶段的径流预测中，将其结果与经验量化标准下的预测结果进行对比。

3 实例分析

本文收集了长江宜昌站1890—2000年共111a的年径流资料，时间序列变化见图1。经分析，本文p取6。为了充分利用资料信息，每次仅预测1a，如要预测1961年的年径流，用1890—1960年的径流资料，如要预测2000年的年径流，就使用1890—1999年的径流资料。现将1890—1980年资料作为量化标准系数率定阶段资料，对量化标准系数进行率定。

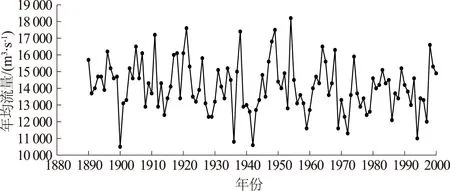
图1 宜昌站年均流量序列Fig.1 Variation of mean annual runoff at Yichang station

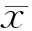
(3)

(4)

式中：x为集合Ai的第j列元素的平均值(i=1，2，3，…，106)，表示第i个集合；j=1，2，3，4，5，6表示Ai中第j个元素)。

按照第2.3节中的步骤(3)—(6)进行计算，结果表明当量化标准系数a=0.1时，预测值平均相对误差取得最小值8.3%，故率定后的量化标准系数a取0.1。

以a=0.1为量化标准系数对1981—2000年的年均流量进行预测，其平均误差为5.2%，e(e为各年份年径流预测相对误差的绝对值)≤10%的合格率为85%，e≤20%合格率为100%；经验量化标准系数a=0.5时，预测平均误差为8.0%，e≤10%合格率为65%，e≤20%合格率为90%，结果对比见表2。从图2也可以看出a=0.1时径流预测趋势也比a=0.5时要更接近实际径流变化趋势。综上，经过率定量化标准后的预测精度比经验取值预测精度有所提高。

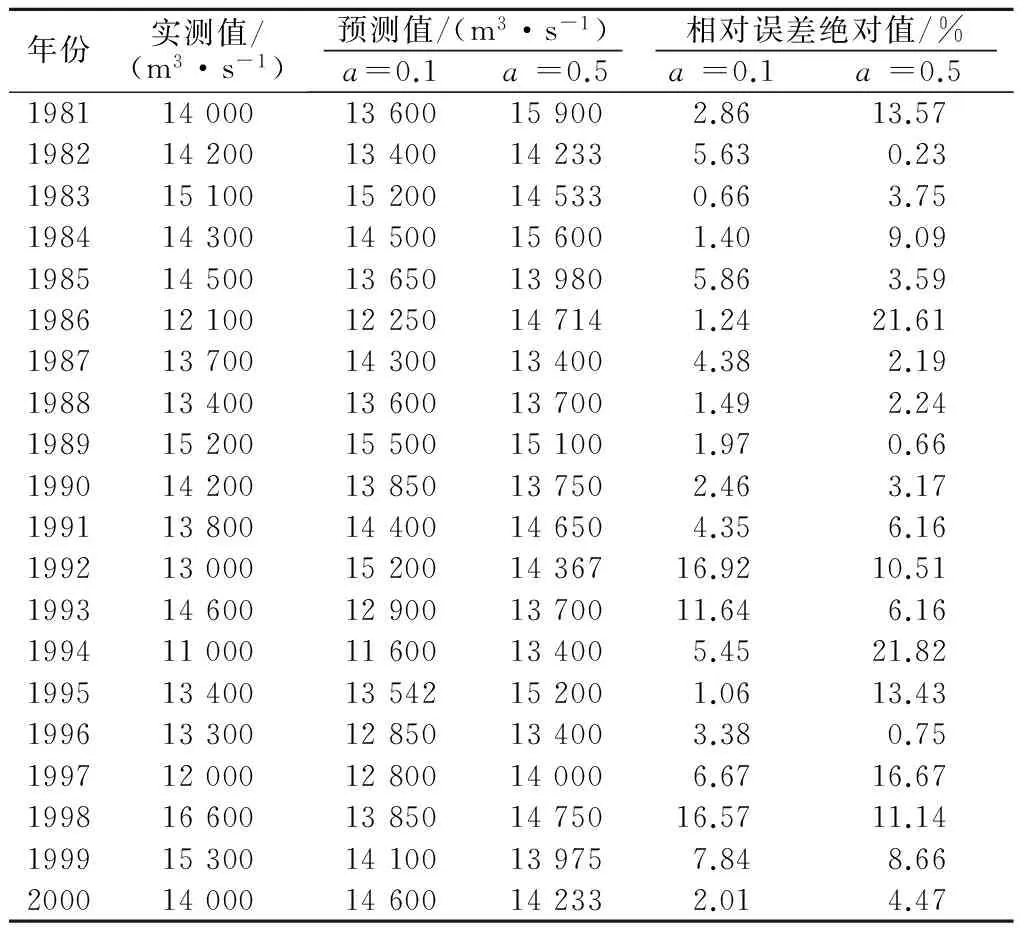
表2 不同量化标准系数年均流量预测结果对比

图2 不同量化标准系数年均流量预测结果对比分析曲线Fig.2 Comparison of predicted data with two quantitative standard coefficients

4 结 语

本文针对集对分析在径流预测中径流集合量化标准仅根据主观经验确定的问题，建立了基于率定量化标准的集对分析预测模型，该模型克服了分类标准主观性确定的缺点。实例分析结果表明该模型有较好的预测精度，充分说明了该模型的实用性及合理性。研究表明：

(1) 将集对分析应用于年径流预测时，首先对量化标准系数进行率定，可有效提高年径流的预测精度。

(2) 仅依据时间序列进行单因素预测的预测方法，并未体现径流本身的变化特性和内部结构，可尝试和与径流有物理成因联系的因素结合，以期进一步提高预测精度。

(3) 如何选择判断集合相似性的指标以及指标的合理性，仍需进一步研究，以便更准确地确定相似集合。

[1] 赵克勤.集对分析及其初步应用 [M]. 杭州：浙江科学技术出版社,2000.

[2] 卢 敏,张展羽,石月珍.集对分析法在水安全评价中的应用研究[J].河海大学学报(自然科学版),2006,34(5):505-508.

[3] 王宏伟,张 鑫,邱俊楠.模糊集对分析法在水资源安全评价中的应用[J].西北农林科技大学学报:自然科学版,2011,39(10):209-214.

[4] 王红芳,丁 晶,王文圣,等.集对分析在频率曲线拟合度定量评价中的应用[J],水利水电技术,2007,38(4):1-3.

[5] 冯利华,张行才,龚建林.基于集对分析的水资源变化趋势的统计预测[J].水文,2004,24(2):11-14.

[6] 刘 冀,徐 刚,彭 涛,等.基于参数优化的集对分析月径流预测[J].水文,2013,33(1):8-11.

[7] 王红芳,黄伟军,王文圣,等.集对分析法在长江寸滩站径流预测中的应用[J].黑龙江水专学报,2006,33(4):3-5.

[8] 覃光华,宋克超,周泽江,等.基于WA-GRNN模型的年径流预测[J].四川大学学报(工程科学版),2013,45(6):39-46.

[9] 欧 源,张 琼,王文圣,等.基于秩次集对分析的年径流预测模型[J].人民长江,2009,40(3):63-65.

[10]王文圣，向红莲，丁 晶.最近邻抽样回归模型在水文水资源预报中的应用[J].水电能源科学,2001,19(2):9 -14.

(编辑：曾小汉)

Prediction of Annual Runoff Based on SPA withCalibration of Quantitative Standard Coefficient

LI Shen-qi1，XIAO Jing-xi3,QIN Guang-hua1,2， ZHANG Ze-hui1

(1.College of Water Resources and Hydropower ，Sichuan University ，Chengdu 610065，China； 2. State Key Laboratory of Hydraulics and Mountain River Engineering，Sichuan University，Chengdu 610065，China; 3.Dazhou Hydrology and Water Resources Survey Bureau，Dazhou 635000，China)

In order to solve the problem that the quantitative standard coefficient is only determined by subjective experience of investigators in annual runoff prediction based on set pair analysis(SPA), we present a prediction model based on SPA in association with calibration of quantitative standard coefficient: Firstly, we calibrate quantitative standard coefficient. Then, we predict the runoff by using SPA. Yichang station in Yangtze River is taken as an example, and predicted data by this model are compared with those by empirical quantitative standard model. The results show that predicted data by the model presented is more accurate to reflect original sequence than those by other models.

variations of water and sediment； calibration of quantitative standard coefficient; set pair analysis(SPA); annual runoff; prediction model; predicted data from empirical standard model

2014-09-15；

2014-09-28

国家973项目(2013CB036401)；国家自然科学基金青年基金项目(51209152)

李深奇(1990-)，男，山西运城人，硕士研究生，研究方向为水文预报、径流模拟，(电话)13835892668 (电子信箱)l_sq129@163.com。

覃光华(1975-)，女，重庆梁平人，副教授，博士，主要从事水文预报、水文计算方面研究，(电话)13668215732 (电子信箱)ghqin2000@163.com。

10.11988/ckyyb.20140799

2016,33(01):6-9

TV121，TV124

A

1001-5485(2016)01-0006-04