对一道省赛压轴题的本源探究与推广*
2016-12-01吴银生
●吴银生
(温州市第八高级中学 浙江温州 325000)
对一道省赛压轴题的本源探究与推广*
●吴银生
(温州市第八高级中学 浙江温州 325000)
2016年浙江省数学竞赛一试最后一题数列题,得分率非常低,问题的根源在于对于此题的本源难以揭示.文章从“整体代换”与“唯一分解”2个角度揭示问题的本源,并进行拓展与延伸.
数列;数学归纳法;整体代换;唯一分解
1 问题提出
题目 给定数列{xn},证明存在唯一分解xn=yn-zn,其中数列{yn}非负,{zn}单调不减,并且yn(zn-zn-1)=0,z0=0.
(2016年浙江省高中数学竞赛一试试题)
本题的得分率非常低,无论教师还是学生都感到无从下手,甚至看标准答案都有点“云里雾里”.究其根源在哪里?是对本题的本源难以揭示.
2 揭示本源
2.1 本源问题1
2.1.1 问题阐述
将zn-zn-1看成一个整体,然后利用代换的思想进行解决.
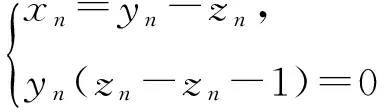
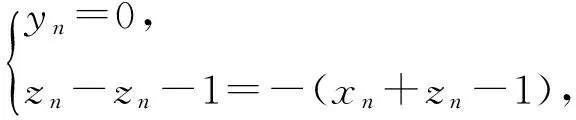
于是有序对
分析 只需证明对任意的正整数n,满足
的(yn,zn)存在且唯一.
下面用数学归纳法证明:
当n=1时,y1(z1-z0)=y1z1=0,从而
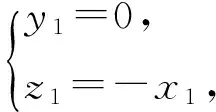
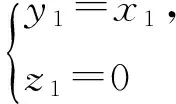
假设当n=k时,命题成立,则当n=k+1时,命题等价于
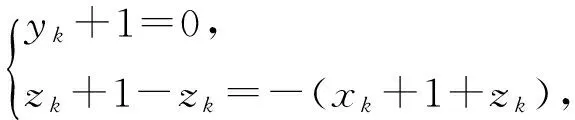
若xk+1+zk≥0,则
于是
若xk+1+zk<0,则
于是
命题成立.
因此,对于任意的自然数n,命题均成立,原问题得证.
2.1.2 追溯考题
“整体代换”的思想在解决一些习题中常常能发挥别样的精彩.
例1 已知f(x)=ax2+bx,满足1≤f(-1)≤2且2≤f(1)≤4,求f(-2)的取值范围.
解 由已知可得f(1)=a+b,f(-1)=a-b,则
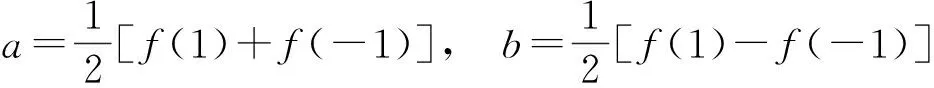
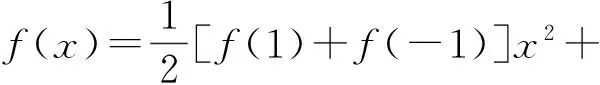

于是
f(-2)=f(1)+3f(-1).
又f(-1)∈[1,2],f(1)∈[2,4],故f(2)∈[5,10].
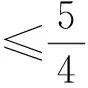
解 同例1,可以用f(0),f(1),f(-1)来表示a,b,c.因为f(-1)=a-b+c,f(1)=a+b+c,f(0)=c,所以

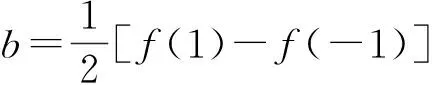
c=f(0),

f(0)(1-x2).
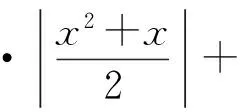
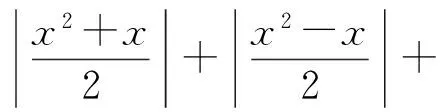
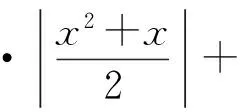
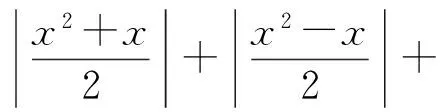
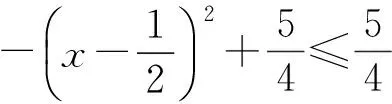
2.2 本源问题2
2.2.1 问题阐述
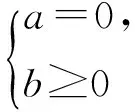
分析 当n=1时,y1z1=0,则
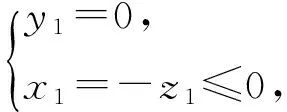
从而x1的正负决定分解方式且唯一.
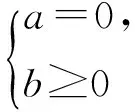
假设当n=k时,xk=yk-zk分解唯一.那么,当n=k+1时,令yk+1=ayk,zk+1=bzk,由yk+1(zk+1-zk)=0,即
ayk(bzk-zk)=0,
从而a=0或b=1.又数列{yn}非负,{zn}单调不减,且z0=0,则
yn≥0,zn≥0,
从而
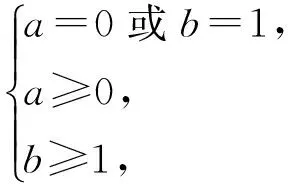
于是
xk+1=ayk-bzk,
即
zk+xk+1=ayk-(b-1)zk.
令b-1=c,则
zk+xk+1=ayk-czk,
其中zk+xk+1,yk,zk是已知的,由n=1时的结论可知分解唯一.
2.2.2 拓展与推广
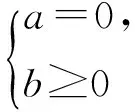
推广1 给定数列{xn},存在唯一分解xn=yn-zn,其中数列{yn}单调不减,{zn}单调不减,且
(yn-yn-1)(zn-zn-1)=0,y0=z0=0.
证明 当n=1时,y1z1=0,则
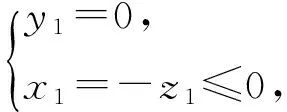
从而x1的正负决定分解方式且唯一.
假设当n=k时,xk=yk-zk分解唯一,那么,当n=k+1时,令yk+1=myk,zk+1=nzk,又(yk+1-yk)(zk+1-zk)=0,即
(m-1)yk(b-1)zk=0,
从而m=1或n=1.又数列{yn}单调不减,{zn}单调不减,y0=z0=0,则y0≥0,z0≥0,从而
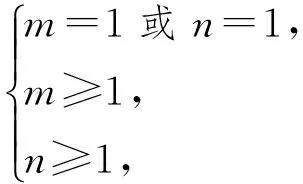
于是
xk+1=myk-nzk,
即
xk+1+zk-yk=(a-1)yk-(b-1)zk.
设a=m-1,b=n-1,则xk+1+zk-yk=ayk-bzk,其中xk+1+zk-yk,yk,zk已知,由上面的结论可知分解唯一.
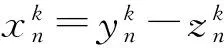
研究发现,当k=0时,推广2显然不成立;当k为负整数时,也不成立,于是笔者猜想:
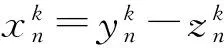
分析 当k为正奇数时,与文首给出的原题证法一致,猜想成立.当k为正偶数时,不妨先证明k=2的情况:
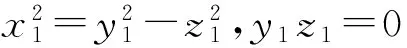
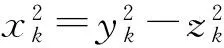
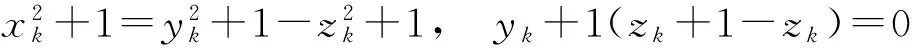
即zk+1=zk,于是
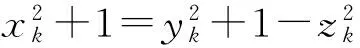
又xk+1,zk是已知的,因此yk+1确定,分解唯一.
在证明方法中,都没有考虑xn=0的情况.由此推广,当k为正偶数时,与k=2证法一致,猜想成立.
�2016-05-19;
2016-06-27
吴银生(1984-),男,浙江温州人,中学一级教师.研究方向:数学教育.
O122
A
1003-6407(2016)11-45-03
