SBPD算法在行程开关故障预测中的研究
2016-12-01陈长骏陈锡爱那文波
陈长骏 王 凌 潘 静 陈锡爱 许 宏 那文波
(中国计量学院机电工程学院,浙江 杭州 310018)
SBPD算法在行程开关故障预测中的研究
陈长骏 王 凌 潘 静 陈锡爱 许 宏 那文波
(中国计量学院机电工程学院,浙江 杭州 310018)
针对行程开关弹簧片的弹力寿命有限的故障,提出了基于状态驻留信息(SBPD)模型的故障预测方法。首先,应用均值与聚类评估指标对行程开关劣化状态进行评估和优化。其次,在对行程开关劣化状态识别的基础上,提出了基于状态驻留信息模型的剩余使用寿命计算方法。最后,在对行程开关进行加速疲劳实验的基础上,应用实验数据将SBPD模型与马尔可夫链蒙特卡罗仿真(MCMC)方法进行验证比较。结果表明,在行程开关弹簧片的弹力寿命有限的故障预测中,SBPD模型优于MCMC仿真方法,可有效预测行程开关剩余使用寿命。
故障预测 行程开关 剩余使用寿命预测 状态驻留预测模型 马尔可夫链蒙特卡罗仿真
0 引言
行程开关广泛应用于电力、工业控制以及自动化等领域,起控制、调节以及限位保护等作用,以实现控制设备自动化。如地铁客室车门上行程开关数量众多,开、关动作频繁造成车门门锁位置行程开关故障率较高[1]。因此,对行程开关进行故障预测研究具有十分重要的意义;掌握其运行状态,合理地获得其剩余使用寿命对整个设备安全和可靠的运行是非常必要的。目前,尚没有研究者对行程开关进行故障预测。
近年来,统计回归建模和劣化状态估计被应用于各种设备的故障预测,文献[2]建立了改进的隐马尔科夫模型,实现了对飞机发动机的剩余使用寿命预测。文献[3]构建了隐半马尔可夫模型,实现了对反应釜的在线故障预报。文献[4]提出了人工神经网络的误差带预测模型,实现了对风电功率的预测。
针对上述预测模型训练样本大、计算复杂且对预测结果依赖于参数的初始化[5](均值和协方差)等缺陷,本文构建了一种计算简单且带有状态驻留信息的预测模型(state-based prognostics with duration information,SBPD),运用于行程开关弹簧片弹力寿命有限的故障,并与马尔可夫链蒙特卡罗仿真(Markov Chain Monte Carlo,MCMC)的方法进行预测比较,结果表明SBPD预测结果优于MCMC。
1 行程开关故障和劣化过程
行程开关由接触点系统、复位弹簧、杠杆、轮轴、滚轮等组成[6],其内部结构如图1所示。在实际应用中,将行程开关常开触点一端置于电源之后,当运动部件撞击到行程开关的杠杆时,限位开关常开触点动作吸和,从而通过将位移信号转换为电信号,实现了对运动方向和终端限位保护等[6]。行程开关故障可分为突发型故障和渐进型故障。渐进型故障可通过对其特征参数进行监测且其表现出逐渐累积的一个发展趋势进行故障预测。本文主要研究行程开关的渐进型故障。

图1 行程开关的内部结构图
行程开关常见的渐进型故障,通常是由于元件从正常到失效过程中耗损以及缺陷不断发展所致,如触头导电性能以及线圈的老化和弹簧片的弹力寿命有限等,其在正常使用中都是依靠定期更换和检修。弹簧片在正常状态时,部件触碰到杠杆后转动α角度常开触点闭合,由于其频繁的闭合、断开导致弹簧片弹力的退化,需转动更大的角度β(β>α)才能闭合,退化到失效状态时甚至一直处于断开状态。本文针对行程开关的弹簧片的弹力寿命有限的故障,通过加速疲劳实验采集行程开关常开触点闭合到断开过程的电压特征参数变化,预测行程开关剩余使用寿命。
2 基于SBPD和MCMC的故障预测模型
利用SBPD和MCMC模型对设备进行剩余使用寿命预测,其步骤包括:确定最优劣化状态数、劣化状态的识别以及剩余使用寿命(remainingusefullife,RUL)预测。
2.1 劣化状态数优化与状态识别
设备从正常到失效需要经历一系列的劣化状态,考虑到劣化状态不可直接观察所得,但可通过性能特征参数的观测值估计其劣化状态。目前,常用的最优状态数确定包括:交叉验证思想、聚类评估指标和专家经验。由于聚类评估指标比其他两个方法更简单易行、计算效率高且更加科学、通用[5],本文采用第二种方法。
常用的聚类评估指标有:CalinskiHarbasz指标[7](CH)、DaviesBouldin指标[7](DB)、Gap指标[8]和Silhouette指标[9]等。本文选用上述4种聚类评价指标来确定最优状态数,其定义式依次分别为:
(1)
(2)
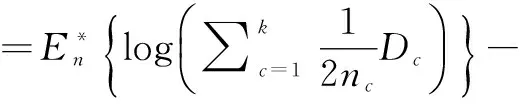
(3)
(4)

本文利用K均值和聚类评估指标进行状态识别,该方法包括两个步骤:训练和识别。假设其聚类数为d,d∈{2,3,...,dmax},将训练集进行K均值聚类,通过4种聚类评估指标获得最优劣化状态数后,得到其聚类中心和类别序号,之后设备任意劣化时刻的观测值都可以利用已训练好的K均值识别当前状态,直至行程开关到达失效状态。K均值聚类方法详细可见文献[10]。
2.2 基于SBPD的RUL预测
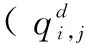
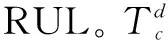
(5)
其中:
(6)
(7)
基于SBPD故障预测过程如图2所示。
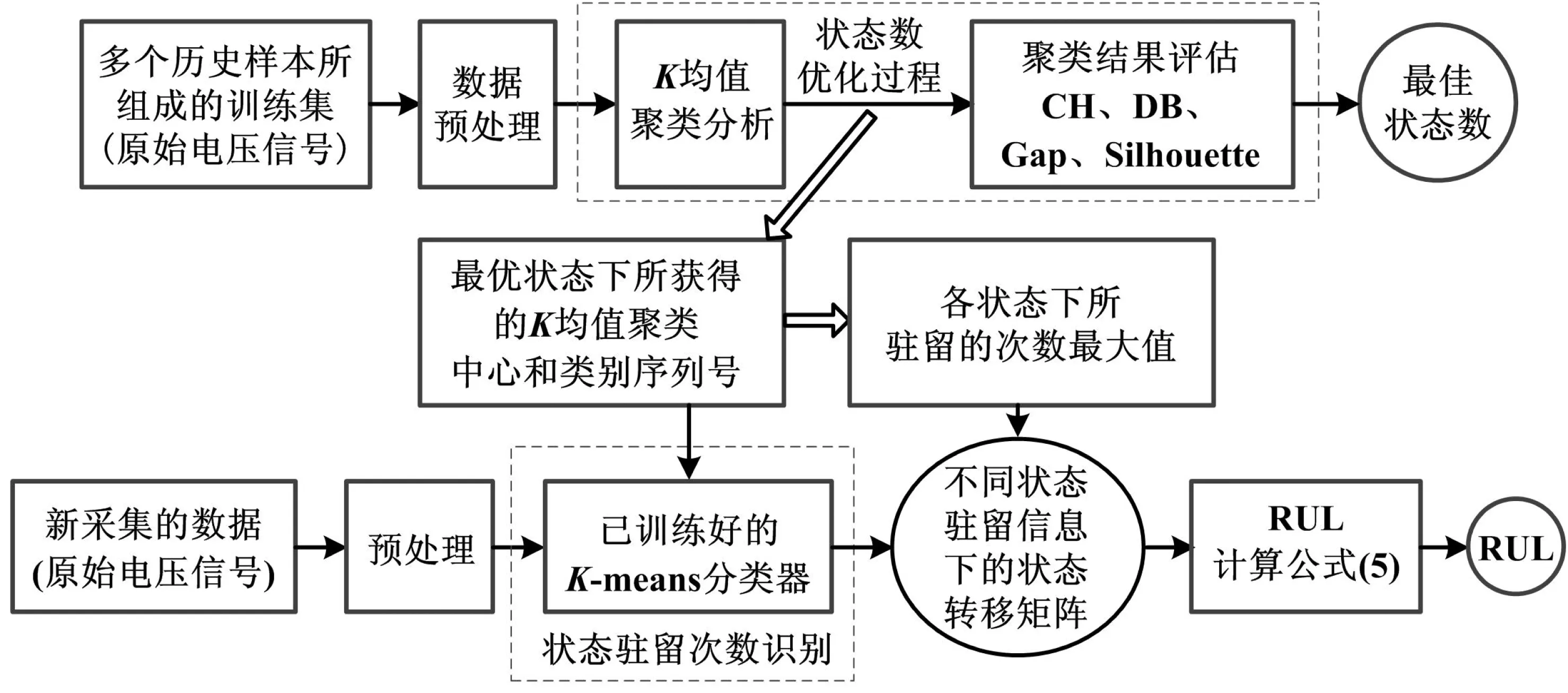
图2 基于SBPD故障预测框架图
2.3 基于MCMC的RUL预测模型
马尔可夫链蒙特卡洛是一种特殊的蒙特卡洛方法,它将随机过程中的马尔可夫链应用到蒙特卡洛模拟中[11],通过按某一分布规律随机抽样,以实现动态模拟。
在劣化状态识别的基础上,可得样本集中的状态并根据马尔可夫过程的性质按式(8)、式(9)计算出训练集中状态之间的一步状态转移矩阵概率。
(8)
qi,i=1-qi,i+1
(9)式中:tran(i,i+1)和tran(i)分别为经一步状态i向状态i+1转移次数和停留在状态i的次数的总和。
在蒙特卡洛仿真过程前,需确定设备当前劣化状态并作为初始化参数的首要步骤,利用(0,1)均匀分布产生随机数与状态转移矩阵相比较,从而决定下一状态的跳变[12],直至到达失效状态,构成一个使用周期,记为Rul(j)。
据式(10)计算出当前状态下的平均剩余使用寿命Meanrul:
(10)
式中:Rul(j)为仿真第j次的剩余使用寿命;Ns为蒙特卡洛仿真的周期数。
3 实验和结果分析
3.1 实验和数据处理
为了验证所提方法的有效性和可行性,进行了行程开关加速疲劳寿命实验。实验装置示意图如图3所示。
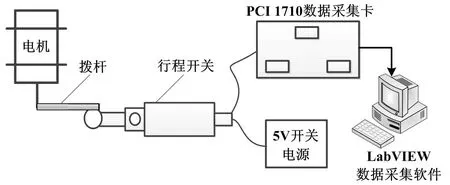
图3 实验示意图
实验装置由匀速电机带动拨杆触发行程开关以及一套基于Lab8.6开发的数据采集系统组成。实验中,将5 V稳压源接入行程开关的常开触点(NO)一端,并将常开触点的另一端接入PCI-1710数据采集卡(输入为电压型),电机转速为120 r/min,采样频率为1 024 Hz。考虑到实验中行程开关的弹簧片弹力有限故障在实际使用中需要经历较长的时间,而渐进型损伤的劣化状态具有指数劣化的趋势[13],且各劣化状态驻留时间较长,故本文对单个行程开关全寿命采集到的数据进行均匀抽样,即通过设置不同的等间隔数从原寿命数据中等间隔抽样出构成一次寿命劣化数据,直至其失效,以组成多个限位开关劣化数据样本。
图4为经抽样后选用db4小波,经软阈值对信号进行消噪处理后组成的一个劣化寿命样本。

图4 限位开关弹簧弹力寿命有限故障抽样后的劣化过程图
3.2 劣化状态数评估及分类
本文抽样共组成9组不同劣化寿命的限位开关样本,其中前7组样本(共106组数据)作为训练集,剩余2组作为测试集,并应用均值聚类对训练集数据进行聚类,聚类数目取2~9,然后分别计算CH、DB、Gap和Silhouette这4类评估值,计算结果如图5所示。从图5可以看出,CH、DB、Gap的最佳聚类数均为6;而Silhouette最优聚类数为2,由于设备劣化需要经历多个劣化过程,故取其次优聚类数6。因此,最后可确定劣化状态数为6类,并应用K均值聚类方法获得聚类中心和类别序号,即可对采集到的数据进行状态识别。
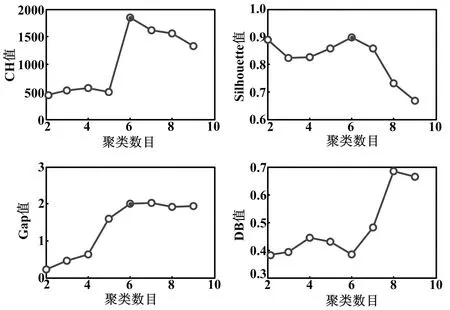
图5 4种聚类评估指标不同状态数目取值对比图
3.3 RUL预测结果比较
通过对多个历史样本所组成的训练集聚类完后得到的类别序号,利用式(6)、式(7)分别计算出行程开关弹簧片的弹力寿命劣化过程中各状态的驻留信息转移概率矩阵,其结果如表1所示。表1中,d表示所有状态下所驻留次数的最大值。
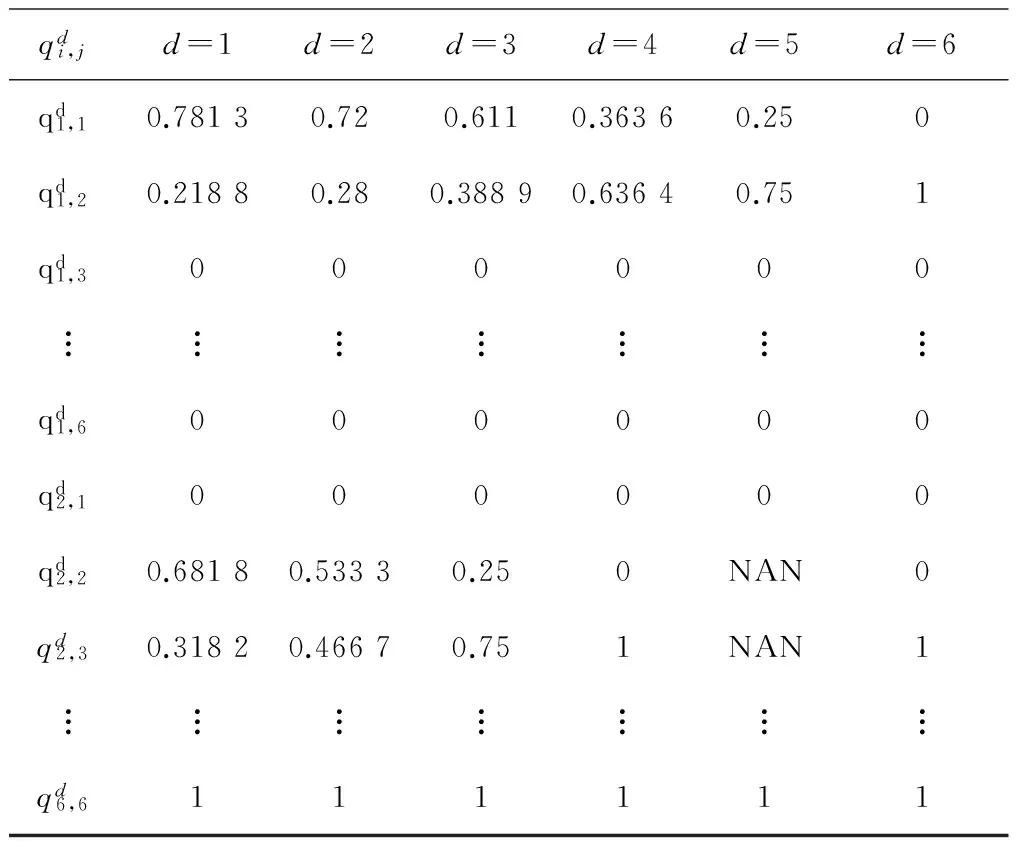
表1 带有驻留信息的状态转移概率矩阵
将每个测试集数据与训练好的均值聚类中心按其平方欧式距离计算,数值最小即可识别出测试数据当前处于哪一类劣化状态,同时判断出该状态所驻留的次数,再对当前状态下的驻留次数,通过表1得出其对应的状态转移概率,最后利用式(5)~式(7)计算剩余使用寿命。本文通过对训练集(前7组)和测试集(第8、9组)共9组全寿命劣化样本,用SBPD方法与MCMC方法分别对其进行剩余使用寿命预测,其结果如图6所示。
从上述预测结果中可看到,基于状态驻留信息的预测方法具有更优预测效果。为了进行定量分析,给出了拟合系数(R-square)以及均方根误差(RMSE)两种定量测试,其计算如式(11)、式(12)所示。
(11)
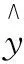
SBPD预测方法有效性检验如图7所示。由图7可以看出拟合系数越高以及均方根误差越小表明预测值与实际值越接近,SBPD方法的RMSE和R-square均优于MCMC方法,充分说明了应用SBPD对行程开关剩余使用寿命预测的有效性。
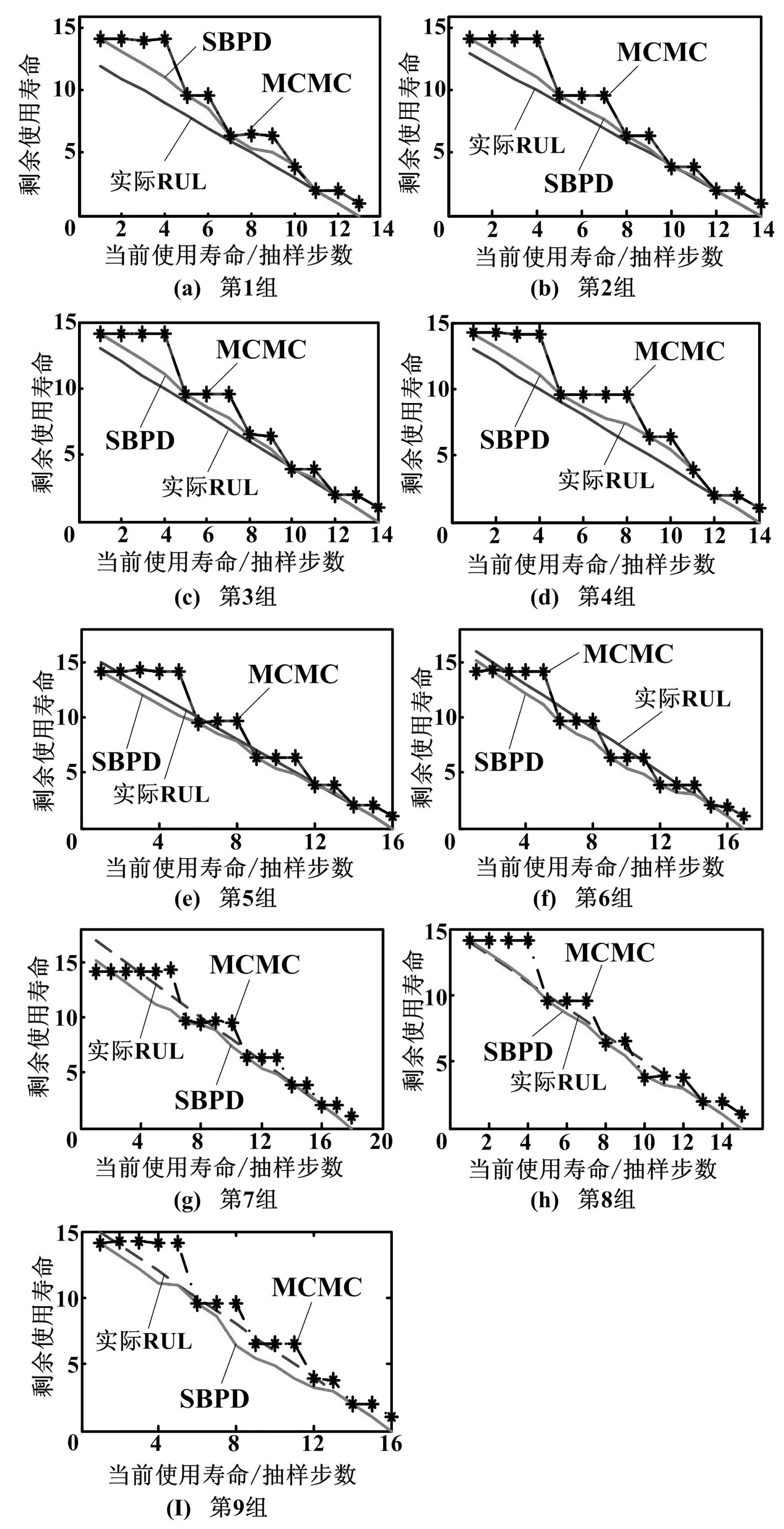
图6 行程开关剩余使用寿命预测图
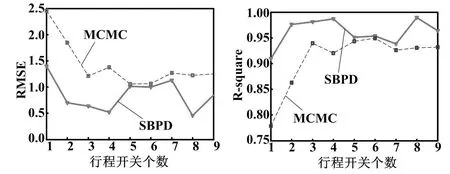
图7 SBPD预测方法有效性检验示意图
4 结束语
在阐述行程开关故障过程基础上,针对其弹簧片
的弹力寿命有限故障,建立了基于状态驻留信息(SBPD)模型的故障预测方法。应用4类聚类评估指标进行状态数优化,通过对行程开关做加速疲劳实验,采集弹簧片的弹力寿命劣化数据,并通过抽样组成不同使用寿命的行程开关样本集。最后利用SBPD模型以及MCMC方法分别计算行程开关的剩余使用寿命。结果比较验证了在行程开关弹簧片弹力寿命有限故障的剩余使用寿命预测当中,SBPD预测模型优于MCMC方法,且SBPD方法具有构造简单预测精度高等优点。本研究同时可为其他设备剩余使用寿命预测的研究提供借鉴。
[10]周世兵,徐振源,唐旭青.新的-均值算法最佳聚类数确定方法[J].计算机工程与应用,2010,46(16):27-31.
[11]石文辉,别朝红,王喜凡.大型电力系统克劳性评估中的马尔可夫链蒙特卡洛方法[J].中国电机工程学报,2008,28(4):9-15.
[12]Camci F,Chinnam R B.Health-state estimation and prognostics in machining processes[J].IEEE Transaction.on Automation Science and Engineering,2010,7(3):581-597.
[13]Gebraeel N,Elwany A,Pan J.Residual life predictions in the absence of prior degraduation knowledge[J].IEEE Transaction.on Reliability,2009,58(1): 106-117.
Study on the Method of State Based Prognostics with State Duration Information (SBPD) in Failure Prediction of Limit Switch
Aiming at the faults caused by limited stretch life of the spring leaf in travel switch,the failure prediction method using state-based prognostics with duration information (SBPD) model is proposed.Firstly,the evaluation and optimization of the deterioration state of the travel switch are conducted by using K-means and clustering evaluation index; then,on the basis of identification of deterioration state,the calculation method of the remaining useful life (RUL) based on SBPD model is proposed; finally,based on the accelerated fatigue experiment of the travel switch,the validation comparison between methods of SBPD model and Markov Chain Monte Carlo (MCMC) simulation is conducted with the experimental data.The results show that the SBPD model is better than MCMC simulation in prediction of faults caused by limited stretch life of the spring leaf; it can effectively predict the remaining useful life of the travel switch.
Fault prediction Travel switch Prediction of remaining useful life SBPD model MCMC simulation
浙江省自然科学基金资助项目(编号:LY14F030019、LQ14F050003)。
陈长骏(1990- ),男,现为中国计量学院控制理论与控制工程专业在读硕士研究生;主要从事故障诊断和故障预测方面的研究。
TH17;TP29
A
10.16086/j.cnki.issn1000-0380.201601006
修改稿收到日期:2015-04-26。
