具有非线性奇异项和变指数的拟线性椭圆问题解的存在性
2016-11-30初颖贾小宁
初颖,贾小宁
(长春理工大学 理学院,长春 130022)
具有非线性奇异项和变指数的拟线性椭圆问题解的存在性
初颖,贾小宁
(长春理工大学 理学院,长春 130022)
针对于具有奇异项和变指数的拟线性椭圆方程Dirichlet边值问题,给出了证明该问题解的存在性的方法。首先构造一个逼近问题,利用Sobolev嵌入定理和变指数的上下确界,克服了来自奇异项和变指数的困难,证明了逼近问题解序列的有界性,然后通过选取适当的检验函数和先验估计技巧克服了来自p-Laplace算子的困难,再借助于逼近问题解序列的有界性,得到了该问题解存在的充分条件。通过对比,采用的逼近方法要优于以往常用的上下解方法。
拟线性椭圆问题;非线性奇异项;变指数;存在性
本文主要研究如式(1)具奇异项和变指数的拟线性椭圆方程解的存在性:
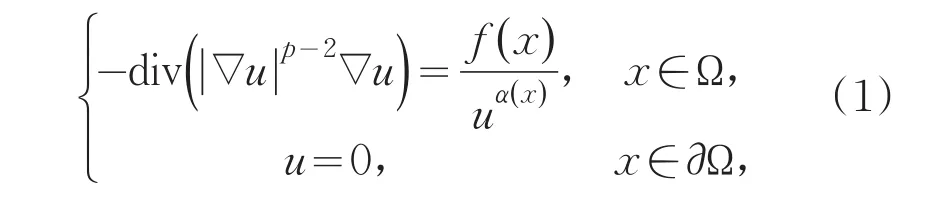
其中,Ω是RN(N≥p)上边界光滑的有界开集,p>2,α(x)是连续函数,是某些Lebesgue空间中的非负函数。
近年来,关于带有奇异项的拟线性椭圆问题引起了国内外众多数学学者的兴趣,并取得了一定的成果。文献[1]和[2]的作者们讨论了问题(1)当p=2,α(x)是常数α时的情形,在假设 f(x)具有某些光滑性或 f(x)∈L2(Ω)的情形下,证明了该问题解的存在性。之后Zhang和Cheng[3]推广了之前的结果,他们研究了问题(1)当 p=2,方程右端项为f(x)g(u)时的情形,其中g(s)在s=0点处奇异,在假设 f(x)∈Cα(Ω)的情况下得到了该问题古典解的存在性。
2010年,Santos[4]对如下具奇异项和超线性项的拟线性椭圆问题进行了研究
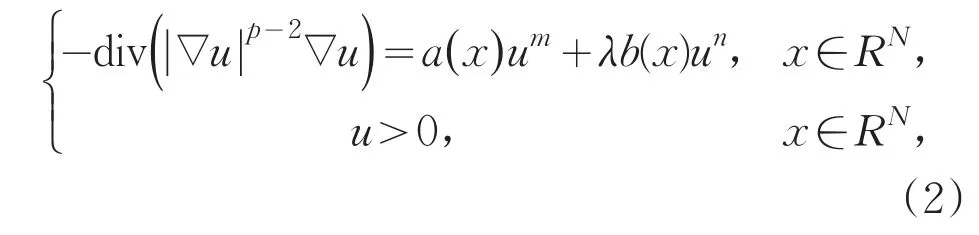
最近,Chu和Gao在文献[5]中研究了如下形式的具奇异项的拟线性椭圆问题
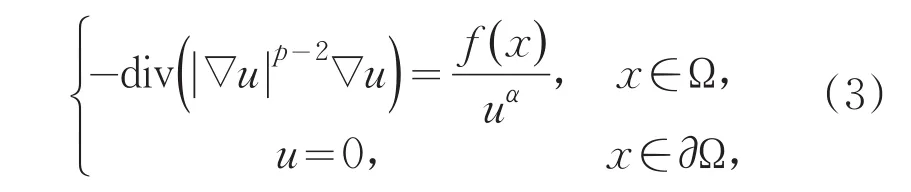
本文推广了[5]的结果,考虑了问题(3)当α是变指数的情形,该问题的难点在于:首先,非线性微分算子是p-Laplace算子;其次,右端项在0点处具有奇异性;最后,奇异项中含有变指数α(x)。这些都为该问题的研究增加了一定的困难。作者们利用类似逼近的方法,Schauder不动点定理,极大值原理,借助于α(x)的上下确界克服了这些困难,证明了对于合适的m和α(x),该问题在中一定有解。
1 预备知识
为了得到问题(1)解的存在性,先介绍一些基本知识和相关引理,首先给出问题(1)弱解的定义。
定义1.1 如果
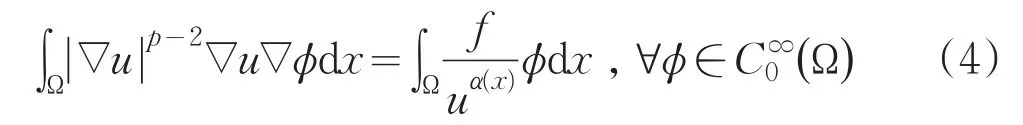
考虑如下逼近问题
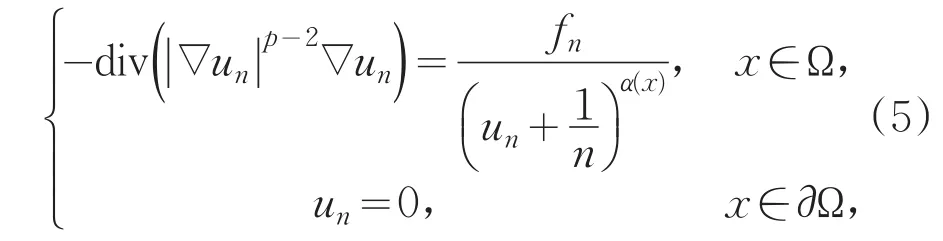
引理1.1 对任何固定的n∈N*,问题(5)在中都有唯一的非负解。
引理1.2 逼近问题(5)的解序列{un}关于n是递增的,且对每个Ω′⊂⊂Ω都存在一个正常数CΩ′使得对每个n∈N*和每个x∈Ω′,都满足
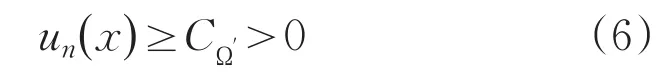
引理1.1 和引理1.2的证明过程参见文献[5]。
2 主要结果
本文只考虑当0<α-≤α(x)≤α+<1的情形,证明:当f具有比L1(Ω)更高的正则性时,问题(1)在中有解。
引理2.1 令un是问题(5)当0<α-≤α(x)≤α+<1时的解,且假设则序列un在中有界。
证明:选取un作为问题(5)的检验函数,由Ho¨lder不等式,利用 fn≤f得
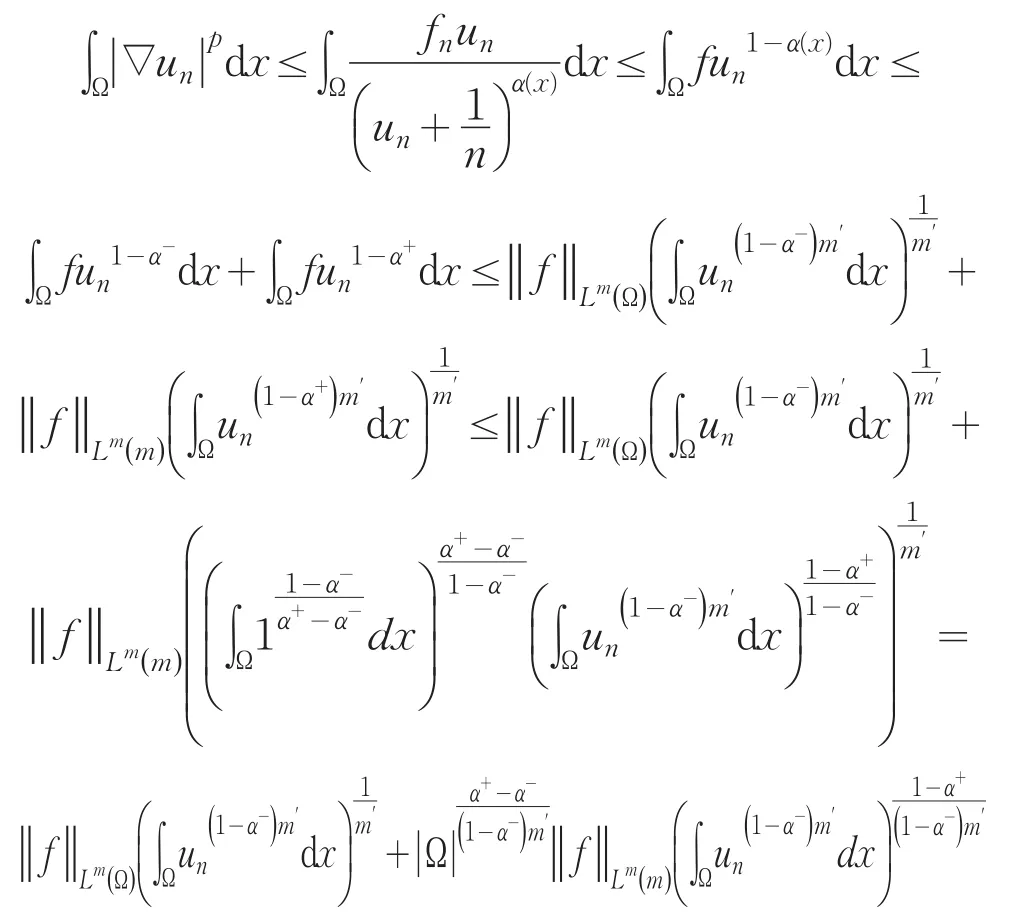
用Sobolev嵌入定理得:
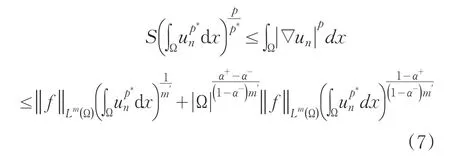
也就是:

由此得到un在中的有界性,由这个估计和式(7)得到结论。
一旦得到了un的有界性,就能够证明出问题(1)解的存在性。
定理2.1若 f是Lm(Ω)中非负函数,
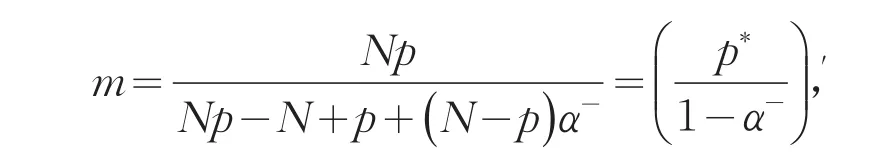
f不恒等于0,且0<α-≤α(x)≤α+<1,那么问题(1)在中有解,且满足(4)式。
证明:由引理2.1知un在中有界,且由引理1.2知un在Ω上逐点收敛于u,由此可以抽序列{un}的子列,在这里仍记为{un},存在u∈W1,p(Ω)
在W1,p(Ω)中un弱收敛于u,
在Lp(Ω)中un强收敛于u,
在Ω中un几乎处处收敛于u,
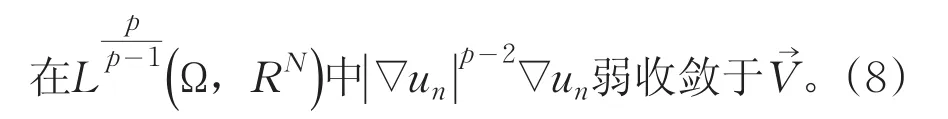
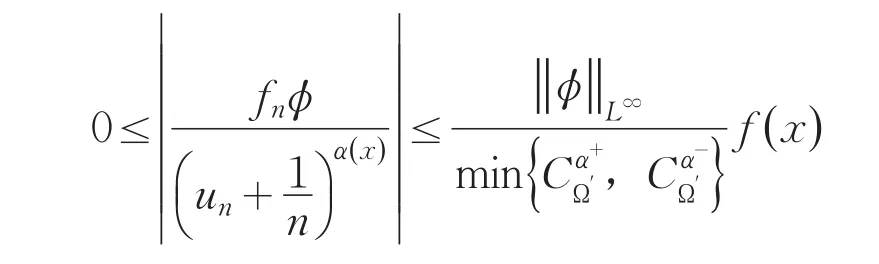
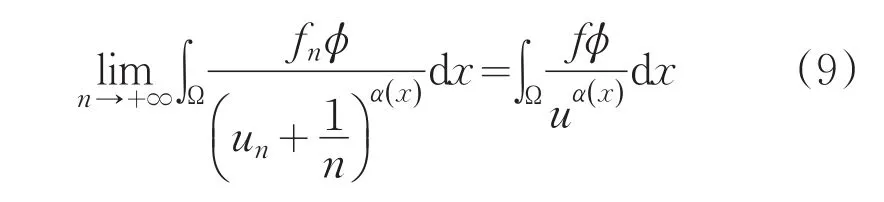
由于un满足下面的恒等式
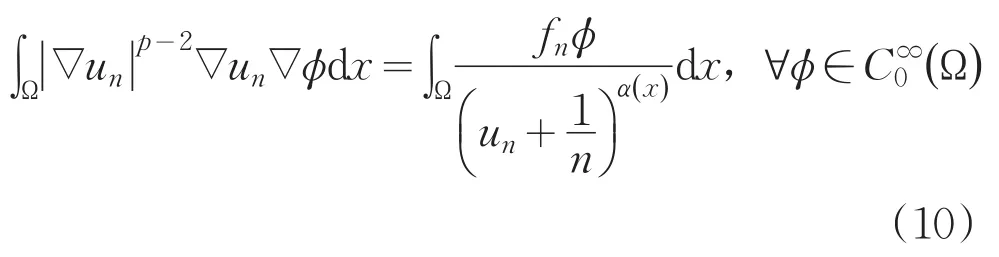
结合(8)-(10)得
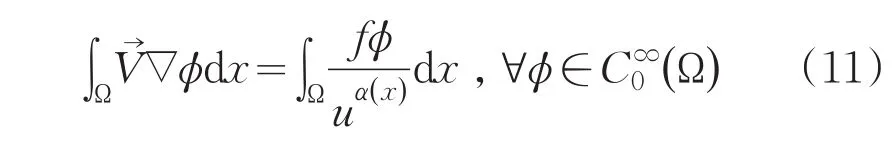

在式(13)中令n→∞,同时利用(11)式得
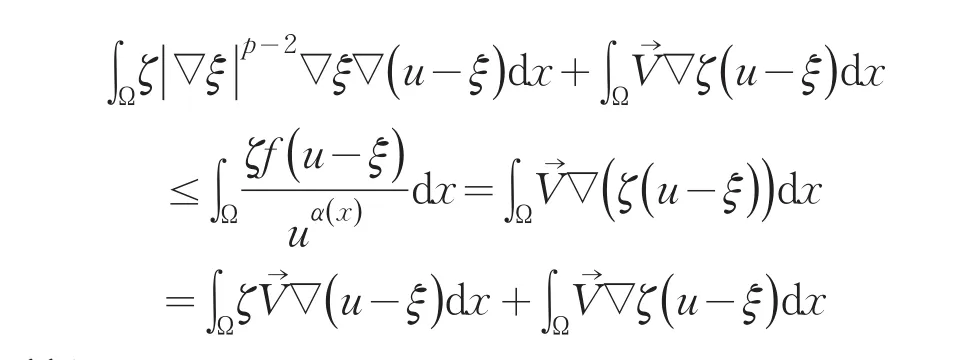
所以
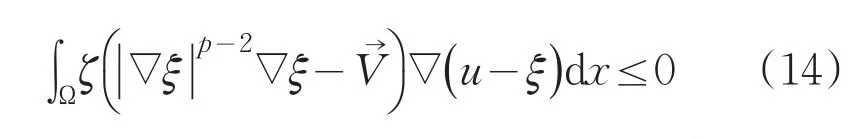
在式(14)中令u-ξ=εψ,其中ψ是W1,p(Ω)中的任意函数,且ε>0是一个常数,我们得到
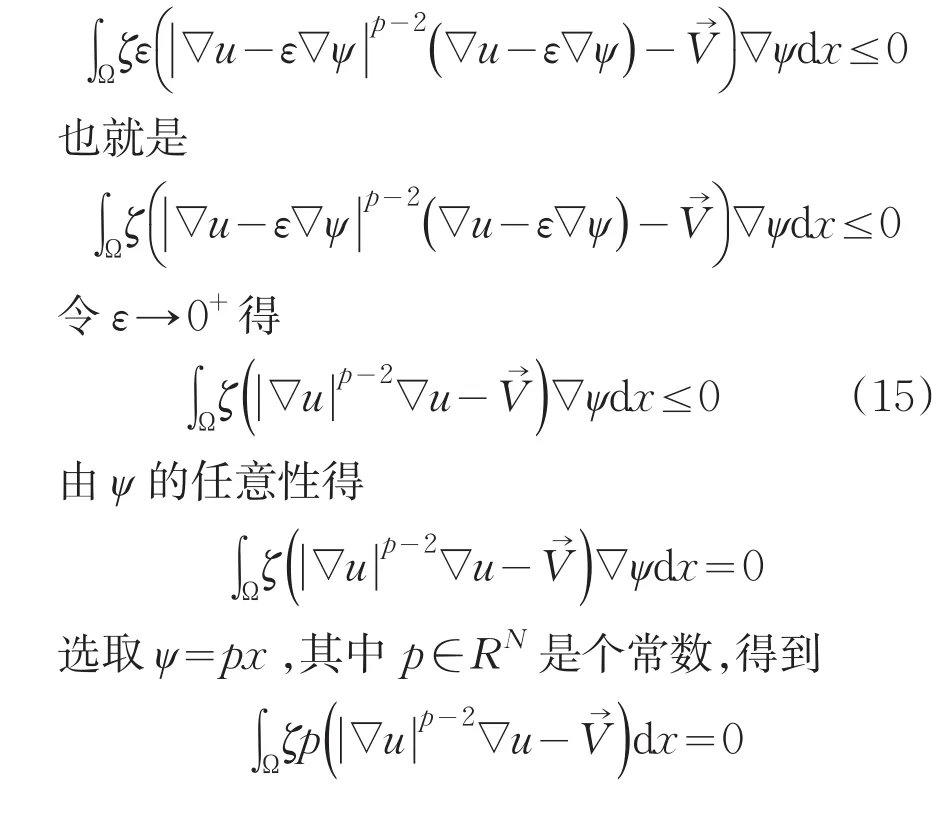
[1] Lazer A C,Mckenna P J.On a singular nonlinear elliptic boundary value problem[J].Proc.Amer. Math.Soc.,1991,111(3):721-730.
[2] Lair A V,Shaker A W.Classical and weak solutions of a singular semilinear elliptic problem[J].J. Math.Anal.Appl.,1997,211(2):371-385.
[3] Zhang Zhijun,Cheng Jiangang.Existence and optimalestimates ofsolutions forsingularnonlinear Dirichlet problems[J].Nonlinear Anal.,2004,57(3): 473-484.
[4] Santos C A.Non-existence and existence of entire solutions fora quasilinearproblem with singular and super-linear terms[J].Nonlinear Analysis,2010,72:3813-3819.
[5] Chu Ying,Gao Wenjie.Existence of solutions to a class of quasilinear elliptic problems with nonlinear singular terms[J].B.V.P.2013,2013:229.
Existence of Solutions to a Class of Quasilinear Elliptic Problem With Nonlinear Singular Term and Variable Exponent
CHU Ying,JIA Xiaoning
(School of Science,Changchun University of Science and Technology,Changchun 130022)
In this paper,we proved the existence of the solutions for the Dirichlet boundary value problem of quasilinear elliptic equation with singular term and variable exponent.Firstly,we constructed an approximation problem,using Sobolev embedding theorem and the supremum and infimum of the variable exponent to overcome difficulties arising from singular term,thus we prove the boundedness of the solution sequence for the approximation problem,then we solved the difficuties caused by p-Laplace operator by selecting the suitable test functions and a priori estimate technique,and with the help of the boundedness of solution sequence for the approximation problem,the sufficient conditions of the existence of solutions for this problem are obtained.By contrast,the approximation method we used in this paper is better than the upper and lower solution method in the past.
quasilinear elliptic problem;nonlinear singular term;variable exponent;existence
O175.2
A
1672-9870(2016)05-0123-04
2016-07-01
初颖(1984-),女,博士,讲师,E-mail:chuying_12345@sina.com
