不同材料储罐底板中Lamb波频散曲线的绘制与对比分析

程 莉，焦 阳，李光海

(1.河北科技大学信息科学与工程学院，河北石家庄 050018；2.中国特种设备检测研究院，北京 100013)



不同材料储罐底板中Lamb波频散曲线的绘制与对比分析

程 莉1，焦 阳1，李光海2

(1.河北科技大学信息科学与工程学院，河北石家庄 050018；2.中国特种设备检测研究院，北京 100013)

Lamb波频散特性是进行Lamb波无损检测的前提，为了给储罐底板的Lamb波检测提供参考依据，根据Rayleigh-Lamb方程，采用二分法求解无限大板中Lamb波的频散曲线，再通过Matlab软件对求解过程进行编程，绘制出Lamb波在不同储罐底板材料中传播的相速度和群速度曲线。为便于对比分析，绘制出各种材料S0模态相速度频散特性曲线及A0模态相速度频散特性曲线。通过对不同材料频散特性的分析与比较，获取对各种材料Lamb波检测可选的模态为S0和A0模态，针对S0模态和A0模态分别给出了每种材料在实际检测中可选的频厚积范围。

超声学；Lamb波；频散曲线；储罐底板；无损检测

程 莉，焦 阳，李光海.不同材料储罐底板中Lamb波频散曲线的绘制与对比分析[J].河北工业科技,2016,33(5):385-391.

CHENG Li, JIAO Yang, LI Guanghai.Drawing and comparative analysis of Lamb wave dispersion curves in tank bottom plate of different materials [J].Hebei Journal of Industrial Science and Technology,2016,33(5):385-391.

随着科学技术的发展，大型储罐在工业生产和国家战略储备中的应用日益广泛且种类复杂多样。储罐底板受所在地环境的影响容易产生腐蚀，导致结构失效，所以人们对储罐的安全性能越来越重视。为了更好地对储罐底板这样的大型板状材料进行方便、快捷的检测，弥补传统检测技术的不足，超声导波技术应运而生[1-9]。Lamb波是超声无损检测中最常见的一种导波形式，20世纪初由LAMB先生研究无限大板中正弦波问题而得名。Lamb波检测具有快速便捷的特点，非常适合板形结构的大面积无损检测，而Lamb波的频散曲线就是为不同材料的板结构选择合适的模态和频率进行检测的主要依据[10-13]。本文对超声 Lamb 波的传播及其频散曲线的绘制做了详尽的介绍，绘制出不同储罐底板材料的频散曲线，得到了超声Lamb波在不同材料结构中的传播特性，并分别对不同材料储罐底板的超声Lamb波传播特性和适宜检测的单个模态特性进行了分析，并得出结论。

1 Lamb波的传播特性及Rayleigh-Lamb方程

Lamb波是在具有2个平行表面的结构中传播的，是由横波和纵波相互耦合形成的一种应力波。Lamb波传播的实质是平板中质点的振动，因其是板中的导波，又名为板波，根据平板上下表面质点振动方向不同可以把Lamb波分成对称S和反对称A两种模态[10-18]，如图1、图2所示。

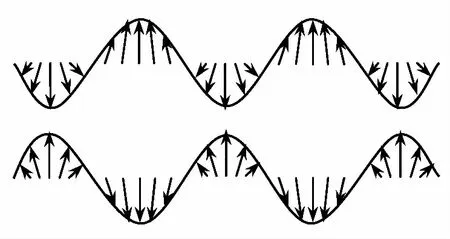
图1 对称型Lamb波Fig.1 Symmetric Lamb wave

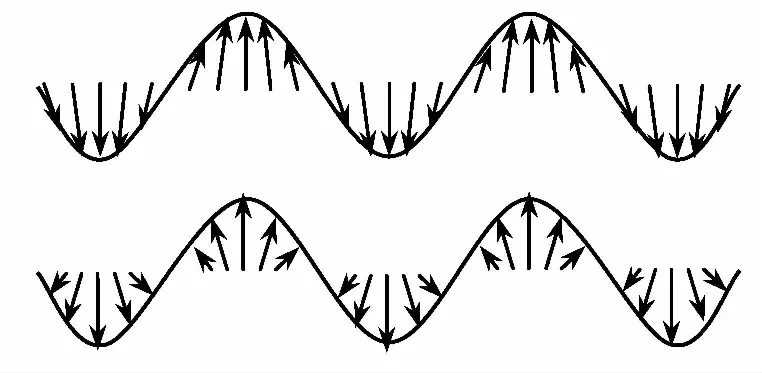
图2 反对称型Lamb波Fig.2 Anti symmetric Lamb wave

每种模式又可以进一步分成相速度不同的若干种模态，分别用S0,S1,S2,…,Sn和A0,A1,A2,…,Am表示。描述Lamb波频散特性的是Rayleigh-Lamb方程[11-18]：

对称模态(S模态)为

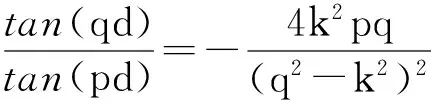
(1)

反对称模态(A模态)为

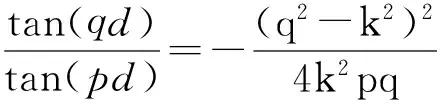
(2)

其中：

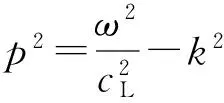
(3)

式中：cL为纵波速度；cT为横波速度；k为波数；f为Lamb波的频率；cP为相速度；d为被测结构厚度的1/2。

cL和cT可由式(4)、式(5)计算：

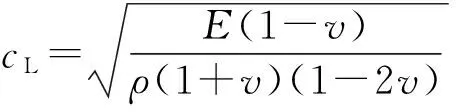
(4)

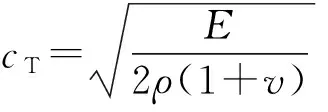
(5)

式中：E为被测结构的杨氏模量；ρ和v分别表示结构所用材料的密度和泊松比。

群速度cg可以通过相速度cP来求解，cg与cP有如下关系[11-12,15-17]：

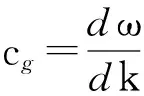
(6)

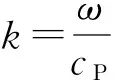
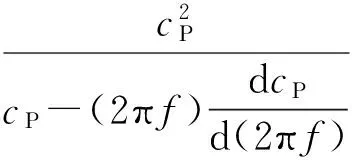
(7)

因为在特定的材料下，其厚度d是一定的，所以式(7)可以表示为群速度cg与频厚积fd的关系：

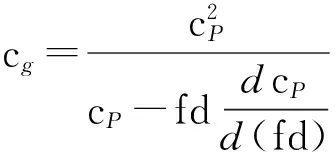
(8)

2 Lamb波频散曲线绘制

由于对称模态与反对称模态的求解方式相同，所以下面以反对称模态为例阐述Lamb波频散曲线的求解、Matlab编程及频散曲线绘制[11]。

2.1 频散曲线求解

由于Lamb波是多模态和频散的，且板状材料的选择决定了横波波速和纵波波速，在厚度一定时一个频率下方程可能有多个解，即有多个模态的相速度cP，因此，将频散方程转变为适当的形式，可以方便得到相速度cP与频厚积fd的关系曲线，继而求得群速度cg与频厚积fd的关系曲线，这些曲线就是Lamb波的频散曲线[16-17]。

以反对称模态为例，将式(3)代入式(2)中可得，

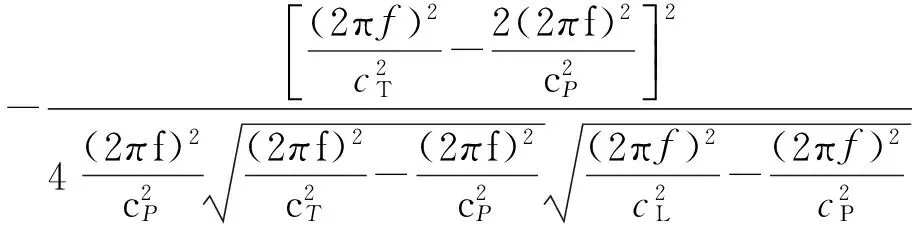
(9)

化简可得：

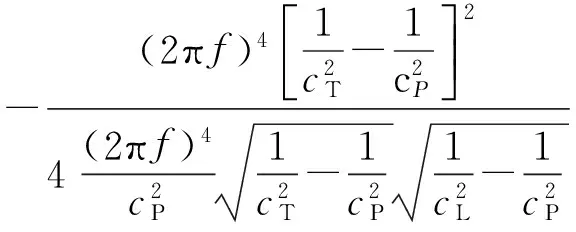
(10)

再约分提取相速度cP后，化简可得：

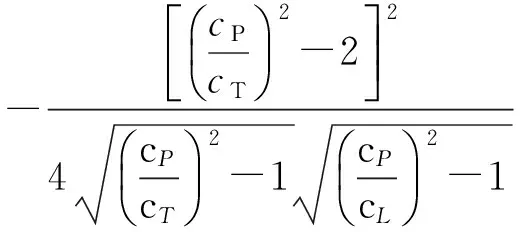
(11)

为了方便求相速度cP与频厚积fd的关系，采用二分法计算，把式(11)转化为各因式相乘的形式，令

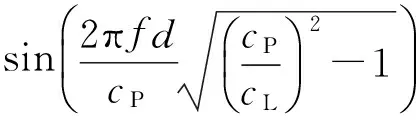
(12)

使各个因式都为实数后，由y=0即可用二分法在Matlab里求Rayleigh-Lamb方程在实数域范围内的解，从而得到频散曲线。

2.2Matlab编程与频散曲线的绘制

使用迭代和二分的方法对Lamb方程进行求解，可以先确定fd在所需范围内的扫描步长，代入方程函数，然后在某一fd下扫描cP，分别代入cP1和cP2的值， 当方程函数值y有为零的或者符号相反时，则有一合适的cP值对应当前的fd，为使方程结果满足所需精度，可以在cP1和cP2之间进行进一步的二分计算[17-22]。

同时，在代入方程时应当考虑cP,cL和cT的关系，确定方程中根号下部分的虚实，从而保证得到的结果是实数解[16]。例如，在程序中为使方程简化，可以令

p=abs(sqrt((cp/ct)^2-1))；

q=abs(sqrt((cp/cl)^2-1))；

则cp<=ct时，p和q都为复数，又由-i*sin(ix)=sinhx和cos(ix)=coshx可将方程化为y=-4*p*q*sinh(pi*fd/cp*q)*cosh(pi*fd/cp*p)+(-p^2-1)^2*sinh(pi*fd/cp*p)*cosh(pi*fd/cp*q)。

同理，当cp>ct且cp<=cl时，y=-4*p*q*sinh(pi*fd/cp*q)*cos(pi*fd/cp*p)+(p^2-1)^2*sin(pi*fd/cp*p)*cosh(pi*fd/cp*q)。

当cp>cl时，y=4*p*q*sin(pi*fd/cp*q)*cos(pi*fd/cp*p)+(p^2-1)^2*sin(pi*fd/cp*p)*cos(pi*fd/cp*q)。

将上述式子在程序中写入1个子程序中，那么在主程序中也可方便调用。

计算完相速度cP与频厚积fd的对应关系后，画出相速度的频散曲线，之后群速度cg则可以直接调用已得数据进行计算，从而画出群速度曲线。

图3即为整个频散曲线绘制的流程图。

根据上述求解方法对Lamb波在储罐底板常用的a3钢板中传播的频散曲线进行了计算，将a3钢板的材料参数E=210GPa，v=0.3，ρ=7.85g/cm3输入程序中，绘制得到相应的相速度频散曲线和群速度频散曲线如图4所示[20-22]。

由图4可得Lamb波频散曲线的特点[11]如下：

1) 在低频情况下，模态较为简单，只有S0和A0 2种模态，而频率越高模态种类越复杂，会同时产生2种以上的模态；

2) 除了S0和A0模态，其他模态都有截止频率，且截止频率以下不存在该模态；

3) 各个模态的群速度不固定，而是随频率增加而上下浮动并逐渐趋向某一固定值。

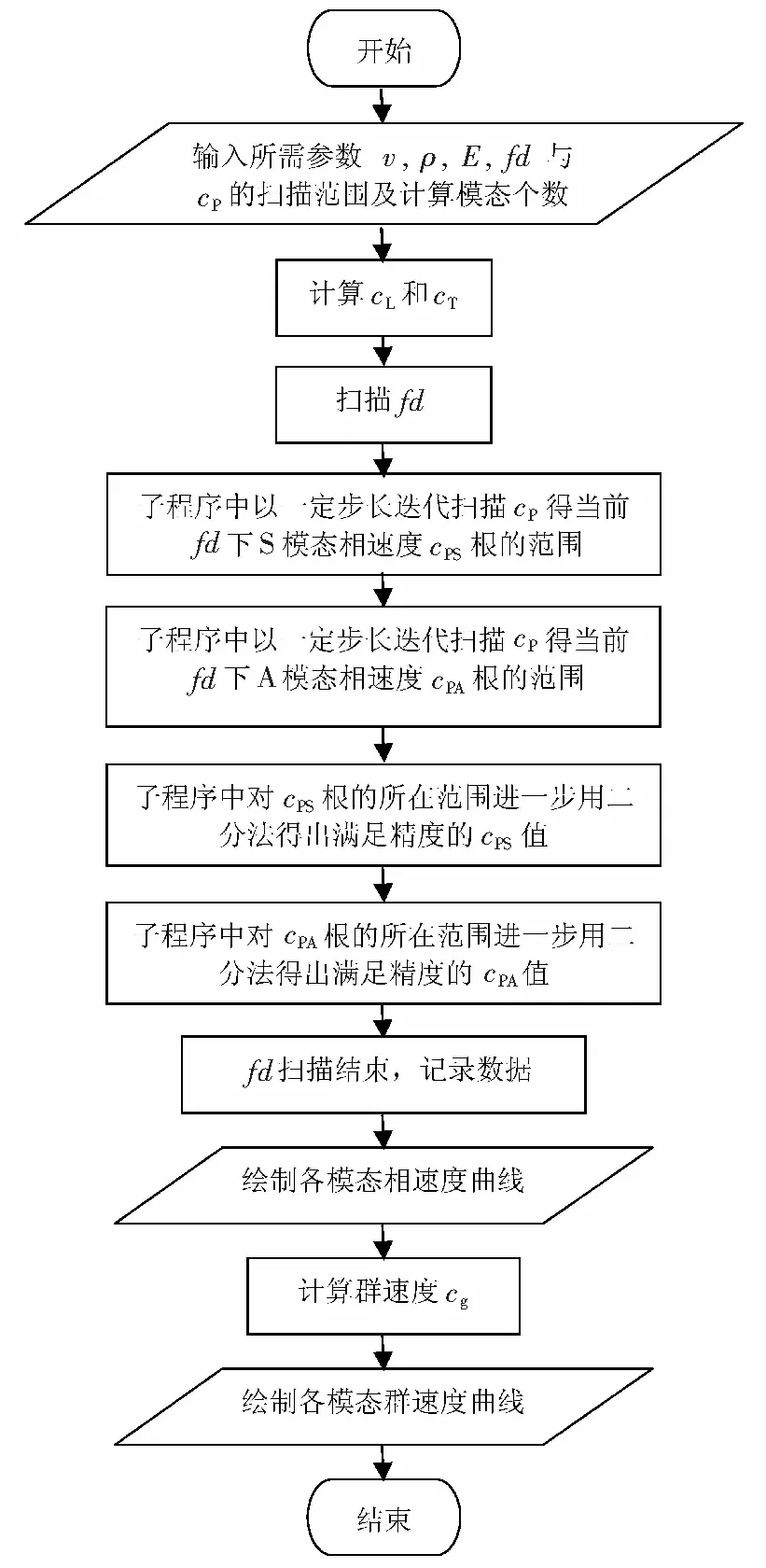
图3 Matlab频散曲线绘制流程图 Fig.3 Flow chart of drawing frequency dispersion curve on Matlab

3 不同材料储罐底板的频散特性分析

为了获取Lamb波对不同储罐底板材料检测可选的模态，选取3种常用的储罐底板材料，即钢板、铝板及玻璃钢板，分别绘制出频散曲线并进行分析比较。算例中已给出钢板的频散曲线，利用上述的计算方法所绘制的另外2种材料的频散曲线如图5、图6所示。

由图4—图6可得不同材料的Lamb波频散曲线的特点：

1) 不同材料的储罐底板的频散曲线大概分布和复杂程度类似，且模态分布简单的情况都在低频厚积时，为使检测中尽可能地克服多模态的问题，最好选用A0和S0模态进行检测；

2) 不同材料的群速度随频厚积的变化而变化的过程相似，而其大小却不太相同，钢板和铝板群速度总体大小接近，钢板的群速度在某些模态下要比铝板高，而玻璃钢的群速度最小。

分析得到，为了方便检测，选择频率和模态时应该尽量选择低频厚积，适合的模态有S0和A0[20-23]，接下来分别对不同材料下这2个模态的相速度进行比较。

3.1 不同材料S0模态相速度频散特性分析

将3种材料的S0模态画在一张坐标图上，如图7所示，3种材料的S0模态走势相同，都是在低频厚积下有稍高的相速度，随着频厚积的加大快速转折到低相速度的位置，并逐渐趋向固定值。

对比后发现，虽然3种材料的曲线走势类似，但是某一频厚积下的相速度大小不同，钢板相速度最大，铝板次之，玻璃钢相速度最小。另外转折点位置不同，玻璃板转折处的频厚积最低，之后是铝板，钢板的转折处频厚积最大。

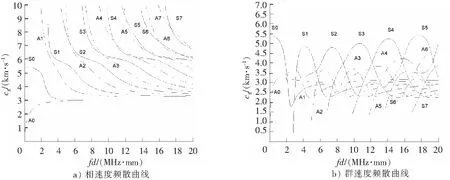
图4 Matlab计算并绘制a3钢板的频散曲线 Fig.4 Frequency dispersion curve of a3 steel plate calculate and drawn by matlab

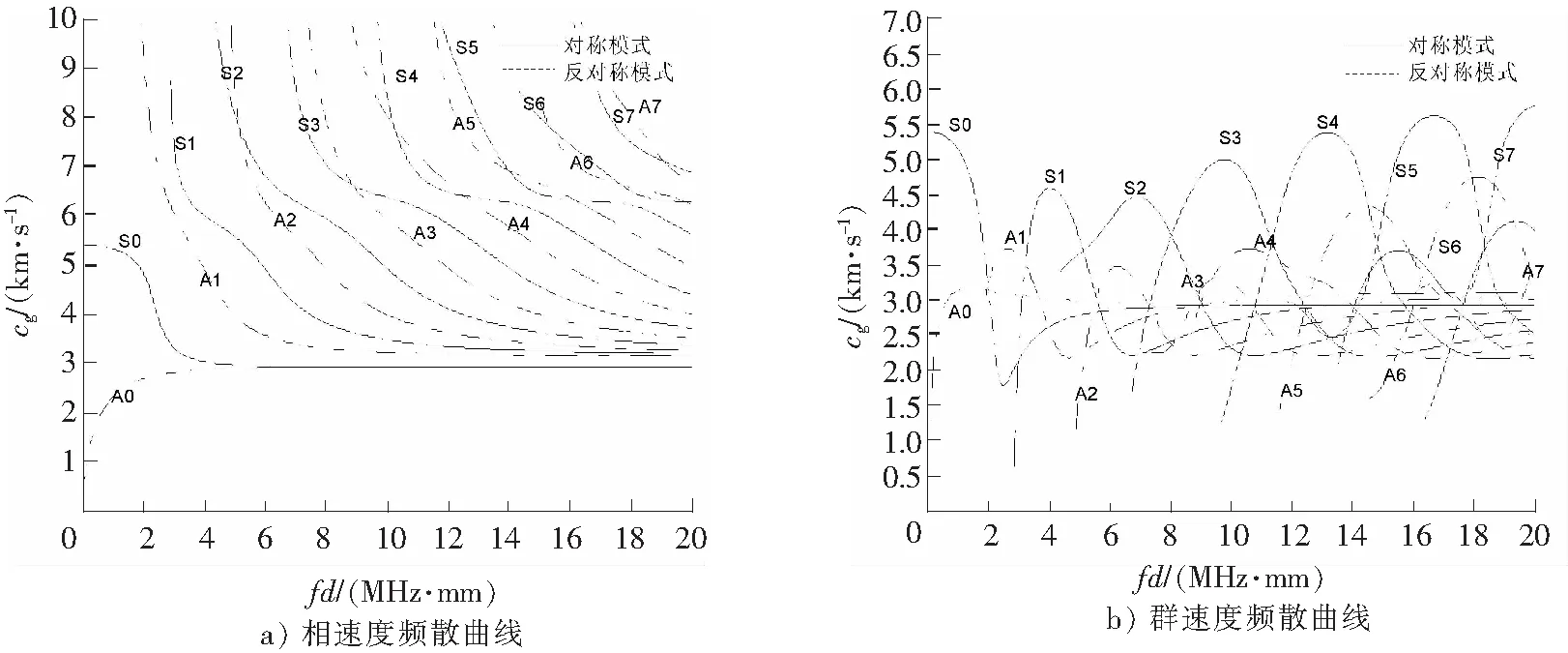
图5 铝板的频散曲线(E=70 GPa，v=0.33，ρ=2.7 g/cm3) Fig.5 Frequency dispersion curve of aluminum plate (E=70 GPa, v=0.33, ρ=2.7 g/cm3)

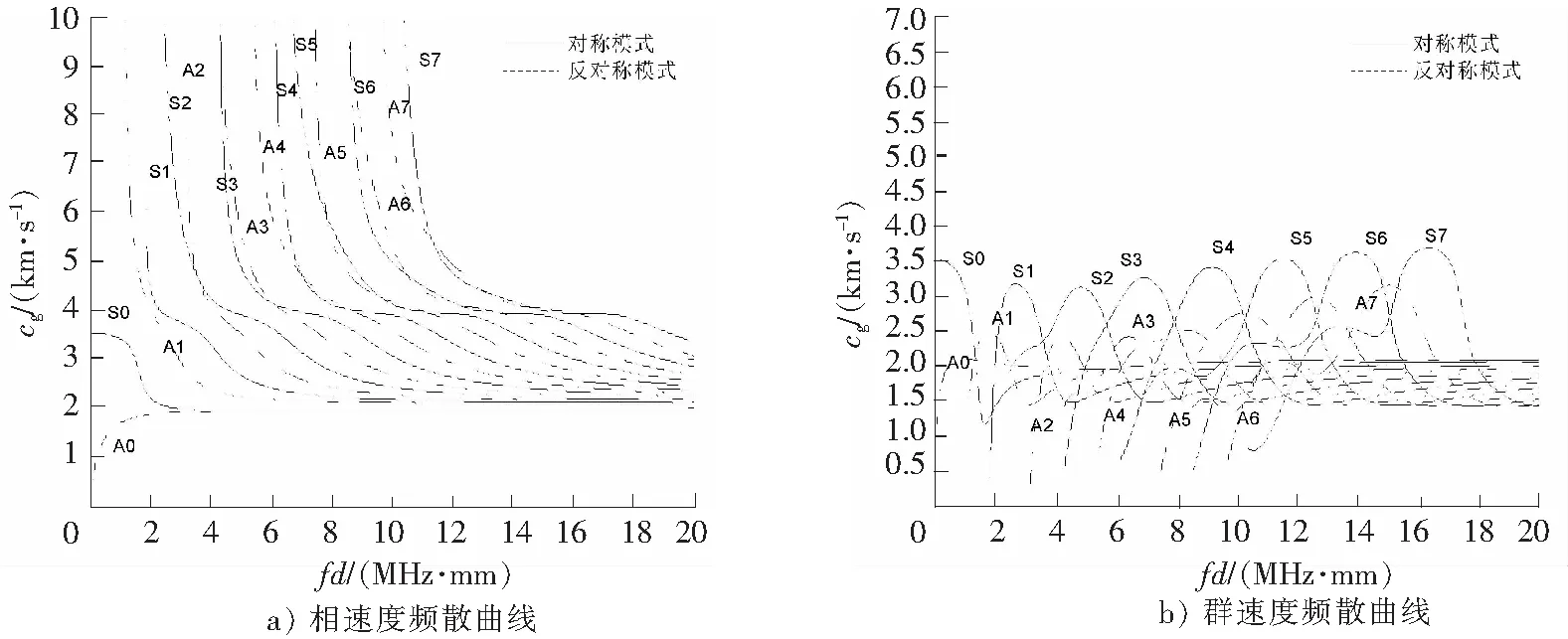
图6 玻璃钢板的频散曲线(E=21 GPa，v=0.3，ρ=1.85 g/cm3)Fig.6 Frequency dispersion curve of glass fibre reinforced plastic plate (E=21 GPa, v=0.3, ρ=1.85 g/cm3)

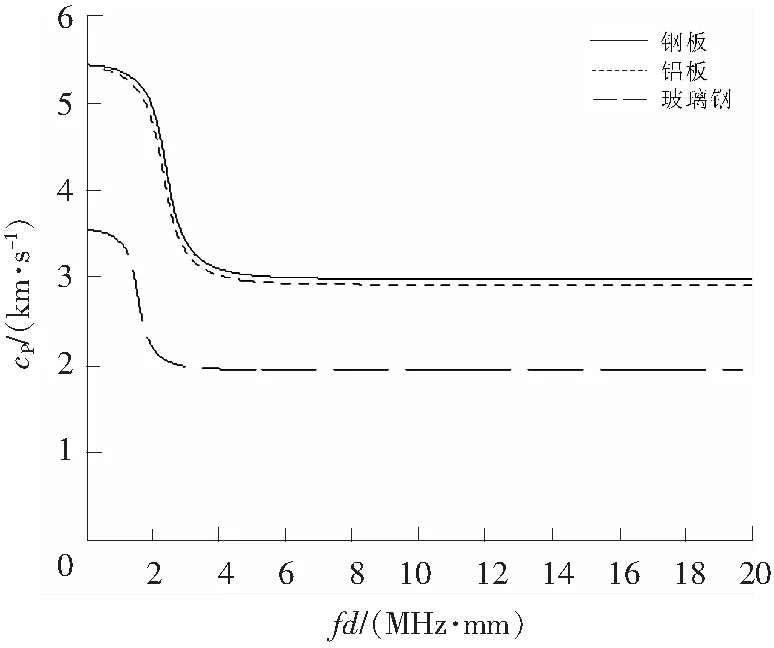
图7 3种材料S0模态相速度频散曲线 Fig.7 Phase velocity curves of S0 modes of three materials

由此可知，不同材料适合检测频厚积的范围不同，钢板范围最宽，为0～2 MHz·mm;铝板次之，为0～1.95 MHz·mm;而玻璃钢可检测范围最窄，为0～1.1 MHz·mm。

3.2 不同材料A0模态相速度频散特性分析

将3种材料的A0模态画在一张坐标图上，如图8所示，3种材料的A0模态走势相同，都是在低频厚积下相速度较低，随着频厚积的加大而相速度逐渐上升，并慢慢趋向1个固定值。

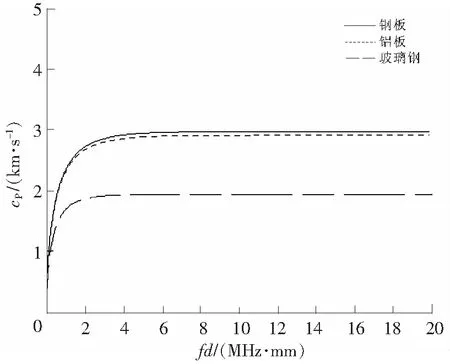
图8 3种材料A0模态相速度频散曲线 Fig.8 Phase velocity curves of A0 modes of three materials

对比后发现，虽然3种材料的曲线走势类似，但是和对称模态相同的是某一频厚积下的相速度大小不同，钢板相速度最大，铝板次之，玻璃钢相速度最小。另外相速度上升的位置不同，玻璃钢上升处的频厚积最低，之后是铝板，钢板的上升处频厚积最大。由此可知，不同材料适合检测频厚积的范围不同，钢板范围最宽，为0.8～2 MHz·mm；铝板次之，为0.8～1.95 MHz·mm；而玻璃钢可检测范围最窄，为0.7～1.1 MHz·mm。

总得来看，在不同材料适合检测的频厚积范围下，S0模态在稍微低频处的相速度相对较大，而A0模态在合适的范围下，则是在相对较高的频厚积处相速度稍大，由此可以进一步缩短范围，便于选取合适频率的激励信号。但由于不同材料的频散曲线不同，可选范围也不相同，还需在检测前对各个材料进行进一步的分析并选取合适频率合适模态的激励源。

4 结 论

本文根据Rayleigh-Lamb方程，采用二分法并通过Matlab编程计算获取储罐底板常用3种材料的频散特性曲线。对3种材料的频散特性曲线进行整体分析，并对S0模态下和A0模态下3种材料的频散特性进行对比分析，得出以下结论：

1)3种材料的相速度和群速度随频厚积的变化趋势相似，但对应同一频厚积其大小不同。钢板与铝板接近，玻璃钢最小。但都在低频厚积时模态分布简单，为使检测中尽可能地克服多模态的问题，应选用A0和S0模态。

2)对于S0模态，3种材料适合检测频厚积的范围不同，钢板范围最宽，为0～2 MHz·mm；铝板次之，为0～1.95 MHz·mm；而玻璃钢可检测范围最窄，为0～1.1 MHz·mm。

3) 对于A0模态，3种材料适合检测频厚积的范围不同，钢板范围最宽，为0.8～2 MHz·mm；铝板次之，为0.8～1.95 MHz·mm；而玻璃钢可检测范围最窄，为0.7～1.1 MHz·mm。

[1] 李杨. 储罐底板超声导波检测传感器研制及应用研究[D]. 北京: 北京工业大学, 2012.

LI Yang. Transducers Development and Application for Ultrasound Guided Wave Inspection on Oil Tank Bottom Plate[D]. Beijing: Beijing University of Technology, 2012.

[2] 王勇，沈功田，闫河，等. 压力容器无损检测——大型常压储罐的无损检测技术[J]. 无损检测, 2005,27(9): 487-490.

WANG Yong, SHEN Gongtian, YAN He, et al. Nondestructive testing of pressure vessels: Nondestructive testing technique for large atmospheric storage tanks[J]. Nondestructive Testing, 2005,27(9): 487-490.

[3] 孙晓云，杨阳，刘东辉，等. 基于ARM & Windows CE的锚杆无损检测系统软件设计[J].河北科技大学学报，2012，33(3)：244-247.

[4] 刘东辉，米博，赵东松，等. 基于HHT的锚杆锚固质量声波无损检测[J].河北科技大学学报，2013,34(4)：208-212.

[5] 帅健，许学瑞，韩克江. 原油储罐检修周期[J]. 石油学报, 2012,33(1): 157-163.

SHUAI Jian, XU Xuerui, HAN Kejiang. Overhaul interval of crude oil tanks[J].Acta Petrolei Sinica, 2012,33(1): 157-163.

[6] 杨志军. 储罐底板磁检测技术研究[D]. 大庆: 大庆石油学院, 2003.

YANG Zhijun. The Study of Magnetic Flux Leakage Technology for the Inspection of Tank Floors[D]. Daqing: Northeast Petroleum University, 2003.

[7] 刘镇清，刘晓. 超声无损检测的若干新进展[J]. 无损检测, 2000,22(9): 403-405.

LIU Zhenqing, LIU Xiao. Development of ultrasonic nondestructive testing techniques[J]. Nondestructive Testing, 2000,22(9): 403-405.

[8] 张清华. 基于超声和涡流的复合式无损检测技术[D]. 广州: 华南理工大学, 2010.

ZHANG Qinghua. Technique of Complex NDT based on Ultrasonic & Eddy Current Testing[D]. Guangzhou:South China University of Technology, 2010.

[9] 宋志东. 超声导波技术在管道缺陷检测中的研究[D]. 天津: 天津大学, 2006.

SONG Zhidong. Study on Pipeline Defects Detection by Ultrasonic Guided Waves[D]. Tianjin: Tianjin University, 2006.

[10] MANSFIELD T L. Lamb wave inspection of aluminum sheet[J]. Materials Evaluation,1975, 33(4):96-100.

[11] 阎石，张海凤，蒙彦宇. Lamb波频散曲线的数值计算及试验验证[J]. 华中科技大学学报(城市科学版), 2010,27(1): 1-4.

YAN Shi, ZHANG Haifeng, MENG Yanyu. Numerical calculation and experimental validation for Lamb wave dispersion curves[J]. Journal of HUST(Urban Science Edition), 2010,27(1): 1-4.

[12]徐可北. 金属薄板兰姆波检验技术[J]. 无损检测, 1999,21(10):461-465.

XU Kebei. Nondestructive testing of metallic plates by Lamb waves[J]. Nondestructive Testing, 1999, 21(10):461-465.

[13]黄志强，王明波，王维斌，等. 基于超声Lamb波技术的储罐底板缺陷检测[J]. 科技导报, 2013, 31(16): 47-50.

HUANG Zhiqiang, WANG Mingbo, WANG Weibin, et al. Defect detection for the bottom plate of oil tank based on ultrasonic Lamb waves[J]. Science & Technology Review, 2013, 31(16): 47-50.

[14]陈强. 基于Lamb波的薄板钢结构损伤识别研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.

CHEN Qiang. Damage Identification Research for Steel Plate Based on Lamb Wave[D]. Harbin: Harbin Engineering University, 2013.

[15]李博成. Lamb波结构损伤识别中信号处理与采集的研究与实验[D]. 成都: 电子科技大学, 2013.

LI Bocheng. Research and Experiment on Signal Processing and Acquisition of Structural Damage Identification based on Lamb Wave[D]. Chengdu: University of Electronic Science and Technology of China, 2013.

[16]陈亮，王恩报，马豪，等. 基于有限元方法的薄板超声Lamb波频散曲线计算[J]. 实验室研究与探索, 2014,33(11): 28-31.

CHEN Liang, WANG Enbao, MA Hao, et al. Calculation of ultrasonic Lamb wave dispersion curve of the thin plate by the finite element method[J]. Research and Exploration in Laboratory, 2014,33(11): 28-31.

[17]许西宁，余祖俊，朱力强. 图解法求解Lamb波频散方程[J]. 电子测量与仪器学报, 2012,26(11): 966-971.

XU Xining, YU Zujun, ZHU Liqiang. A graphical method to solve a dispersion equation of Lamb wave[J]. Journal of Electronic Measurement and Instrument, 2012,26(11): 966-971.

[18]曹正敏，林莉，李喜孟. 兰姆波频散曲线的绘制与试验验证[J]. 理化检验(物理分册), 2008,44(9): 482-500.

CAO Zhengmin, LIN Li, LI Ximeng. Plotting and experimental validation of Lamb wave dispersion curve[J]. Physical Testing and Chemical Analysis. Part: A Physical Testing, 2008,44(9): 482-500.

[19]刘增华，何存富，吴斌. 单层板频散曲线的矩阵表示及MATLAB实现[J]. 无损检测, 2005,27(5): 225-227.

LIU Zenghua, HE Cunfu, WU Bin. Matrix expression for dispersion curve of single plate and its implementation by MATLAB[J]. Nondestructive Testing, 2005,27(5): 225-227.

[20]李迎. 复合材料Lamb波检测中S0单模式信号的提取[J]. 无损检测, 2012,34(8): 30-33.

LI Ying. Extracting the S0 single mode of Lamb wave in composite material[J]. Nondestructive Testing, 2012,34(8): 30-33.

[21]陈军，李志浩，林莉，等. 铝板中Lamb波检测的实验研究[J]. 应用声学, 2011,30(2): 98-104.

CHEN Jun, LI Zhihao, LIN Li, et al. Experiment investigations of Lamb waves in an aluminum plate[J]. Applied Acoustics, 2011,30(2): 98-104.

[22]严刚，周丽. 基于Lamb波的复合材料结构损伤成像研究[J]. 仪器仪表学报, 2007,28(4): 583-589.

YAN Gang, ZHOU Li. Study on damage imaging for composite structure using Lamb wave[J]. Chinese Journal of Scientific Instrument, 2007,28(4): 583-589.

[23]禹化民，王维斌，吕小青，等. 储罐底板缺陷兰姆波检测的影响因素[J]. 无损检测, 2015,37(7): 19-24.

YU Huamin, WANG Weibin, LYU Xiaoqing, et al. Influencing factors for the Lamb wave detection of tank bottom defects[J]. Nondestructive Testing, 2015,37(7): 19-24.

Drawing and comparative analysis of Lamb wave dispersion curves in tank bottom plate of different materials

CHENG Li1, JIAO Yang1, LI Guanghai2

(1. School of Information Science and Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China; 2. China Special Equipment Inspection and Research Institute, Beijing 100013, China)

Lamb wave dispersion characteristic is the precondition of lamb wave nondestructive detection. The article provides an important reference for the Lamb wave detection of the tank bottom plate. Based on the Rayleigh lamb equation, Lamb wave dispersion curves in the infinite plate are obtained according to dichotomy in this paper. Through programming the Matlab software for the solving process, phase velocity curves and group velocity curves that Lamb wave propagate in different tank bottom plat materials are drawn. In order to facilitate the comparison and analysis, the S0 mode phase velocity dispersion characteristic curve and the A0 mode phase velocity dispersion characteristic curve of various materials are also plotted. Through the analysis and comparison of the dispersion characteristics of different materials, the optional mode for Lamb wave detection for different materials are S0 mode and A0 mode. For S0 mode and A0 mode, the optional frequency-thickness product ranges for each material in the actual detection are given, respectively.

ultrasonics; Lamb wave; frequency dispersion curve; tank bottom plate; nondestructive testing

1008-1534(2016)05-0385-07

2016-04-27;

2016-06-17；责任编辑：李 穆

国家科技支撑计划项目(211BAK06B03)

程 莉(1991—)，女，河南周口人，硕士研究生，主要从事超声检测和传感器方面的研究。

焦 阳教授。E-mail:jyang939@163.com

TK172

A

10.7535/hbgykj.2016yx05005