基于最优子段的矩形优化排样
2016-11-30姜永亮
姜永亮, 周 俊
(海南师范大学校园网络中心,海南 海口 571158)
基于最优子段的矩形优化排样
姜永亮, 周俊
(海南师范大学校园网络中心,海南 海口 571158)
为有效解决企业实际生产中的矩形优化排样问题,对矩形优化排样算法进行研究,给出基于最优子段的矩形优化排样算法,有效解决了企业实际生产中的长板矩形优化排样问题。首先基于动态规划算法求出所有小于剪床刀刃长度的最优子段的最佳排样方式,然后以所求的最优子段作为可用子段在长板上进行优化排样,并将矩形优化排样问题转化为完全背包问题。最后基于分支定界技术的整数规划算法对其进行求解。企业应用实例表明该算法在解决长板矩形优化问题方面优于其他算法。
矩形优化排样;最优子段;动态规划算法;分支定界技术
所谓的矩形优化排样问题就是指将需要的多规格、多类型零件排放在给定尺寸的板材上,使板材的利用率最大,该问题是属于NP完备问题[1-2]。在机械制造、家具、玻璃加工等企业经常遇到排样问题:如在规格为 L×W的板材上进行剪切排样,要求剪切出的矩形毛坯的种类最多为m种,每种毛坯在板材上出现的次数不限,排样的目标是使板材中所含毛坯的总价值最大,该类排样称为无约束排样[3]。对于此类问题,国内外学者均进行了相关研究并取得了一定的成果。文献[4]提出了生成矩形毛坯最优T形排样方式的递归算法;文献[5]提出基于匀质条带的矩形件最优三块布局算法;文献[6]提出基于最优两段式排样算法等。对于剪床刀刃不大于板材的最大长度的排样问题,上述算法可以进行有效解决,当遇到剪床刀刃长度小于板材长度的长板排样问题时,上述算法无法解决。对于长板矩形优化排样问题文献[7]提出长板单一尺寸矩形毛坯定长分割优化排样算法;文献[8]提出基于两阶段的分段单一矩形优化排样算法,上述算法仅仅有效解决了单一矩形的长板优化排样问题。对于多规格矩形套排的长板矩形优化排样问题,目前企业常用的算法是基于文献[9]提出的两阶段或三阶段矩形优化排样算法,该算法虽然切割工艺简单,但是在很多情况下原材料利用率不高。在资源日益短缺的今天,节约生产成本也是企业提高经济效益的有效方式。考虑到企业实际生产中切割工艺及原材料利用率对企业经济效益2个因素的影响,这里提出基于最优子段的矩形优化排样算法,并将其应用于系统开发,有效解决了企业实际生产中的长板矩形优化排样问题。
1 相关概念
(1) 条带。若干个矩形零件连续地按照水平或竖直方向排放在一起构成一个条带,如图1所示,其中图1(a)、(b)为X向条带,图1(c)、(d)为Y向条带。
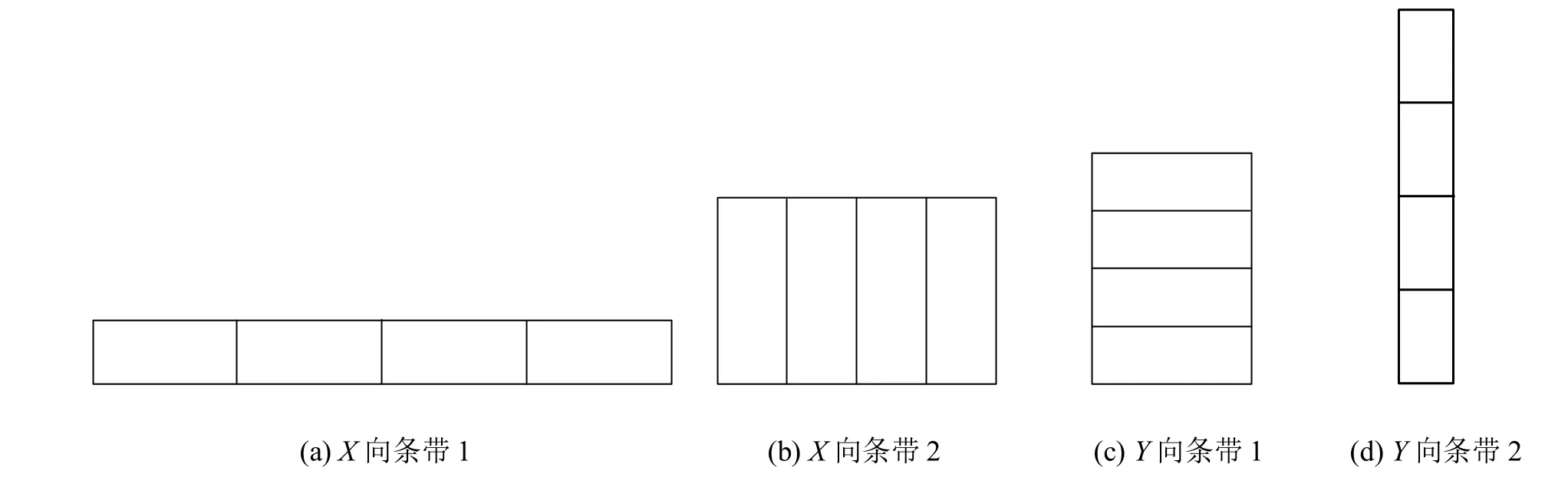
图1 排样中的条带
(2) 同质条带。对于给定尺寸的条带(x×y,其中,x为条带长度,y为宽度),若条带中只含一种矩形零件,该条带称为同质条带如图 2(a)所示,若条带中含多种矩形零件,则称为一般条带如图2(b)所示。

图2 最优条带与一般条带
(3) 子段。假定实际生产中所用板材规格为L×W,在排样过程中将板材分成若干个子段,要求各子段长度均小于剪床刀刃长度LB,图3为板材分成5个子段。
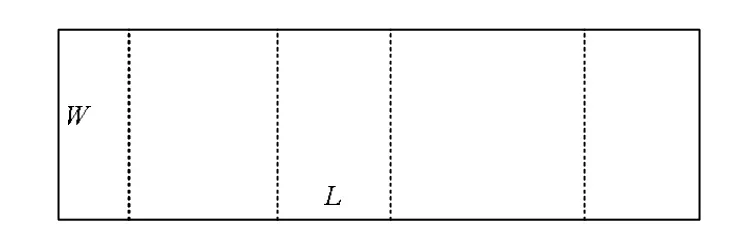
图3 板材分成5个子段
(4) 最优子段。假定在排样中按照某种排样方式对各子段进行优化排样,得到最优排样方式下价值为V的子段有S1, S2,…,Sn,且在长度方面,则称子段S1是价值为V的最优子段。
(5) 两块式排样。对于沿长度方向剪切的子段沿竖直方向将其分成左右两块,如图4所示,可在块内使用同质条带进行排样。对于块S1使用X向条带,对于块S2可以使用X向条带也可以使用Y向条带,若块S2使用X向条带则该子段的排样方式称为FXX排样方式,如图4(a)所示,若块S2使用Y向条带则该子段的排样方式称为 FXY排样方式,如图4(b)所示。鉴于上述假定,最优子段其最优排样方式可以使用求解。
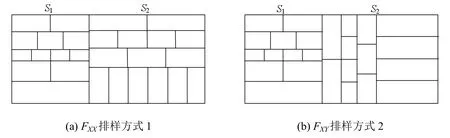
图4 两块式排样
2 基于最优子段的矩形优化排样算法
2.1问题描述
假定某一排样任务中,所用板材长度为L,宽度为W,剪床刀刃长度为LB,待排矩形零件的规格为:,矩形的价值为c1, c2,… ,cm(这里取矩形零件的面积为其价值)。受剪床刀刃长度的限制,企业在实际的生产下料过程中必须先将板材剪切成若干个子段,然后在各子段上进行优化下料。优化排样的求解正好与优化下料过程的求解相反。优化排样的求解过程为:首先求出各子段的最优排样方式,然后使用各子段在长板上进行优化布局。考虑到实际生产中切割工艺对生产效率的影响问题,需对各子段采用基于同质条带的两块式排样方式。鉴于两块式排样是以同质条带为单位进行排样的,在对子段进行两块式排样之前需求出各同质条带的价值。这样基于最优子段的矩形优化排样需要求解如下3个问题:①同质条带求解;②最优子段排样方式求解;③板材最优分段求解。
2.2同质条带求解
规格为x×wi的X向条带其价值可用式(1)求解:

规格为wi×y 的Y向条带其价值可用式(2)求解:

2.3最优子段排样方式求解
规格为x×W的子段,基于同质条带的两块式排样方式的最优价值可用式(3)求解:

式(3)中的VXX为两块均使用X向条带进行排样的最优价值,VXY为一块使用X向条带且另一块使用Y向条带进行排样的最优价值。对于长度为x宽度为k的块,如果基于X向条带进行排样其价值可用式(4)求解:

如果基于 Y向条带进行排样其价值可用式(5)求解:

式(4)、(5)中的 Z均代表的是非负整数集合,int()为取整函数。基于以上描述,对于式(3)中的VXX可用式(6)求解:

VXY可用式(7)求解:

完成式(6)、(7)求解之后,根据式(3)即可求出规格为x×W的子段,基于同质条带的两块式排样方式的最优价值Vx。根据式(8):
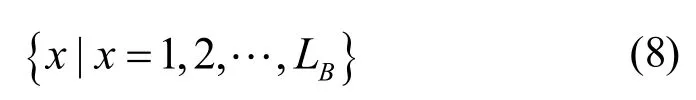
求出所有不大于剪床刀刃长度子段的最优排样价值V1, V2,…,VL及最优排样方式。在 V1, V2,…,VLBB中若有,则长度为k的子段价值称为Vk的最优子段,按上述规则求出所有小于等于剪床刀刃长度最优子段的价值、长度及最优排样方案,即完成了最优子段最优排样方式的求解。式(4)、(5)从数学模型上分析均属于背包问题,考虑到动态规划算法具有存储记忆功能,这里使用动态规划算法对其进行求解。
2.4板材最优分段求解

其中,N1,N2,… ,Nn1为最优子段在板材上出现的次数。对于式(9)使用基于分支定界的整数规划算法对其进行求解,求出板材的最优分段,进而求出长板矩形优化样的最终排样结果。
3 应用实例
为验证算法的有效性,这里基于 C#语言开发一矩形优化排样系统,系统对AutoCAD进行了二次开发,所有排样结果以CAD格式输出。配置CPU主频2.10,1 G内存即可运行本系统。
实例 1. 国内某拖车生产企业使用本系统对长板进行优化矩形下料。零件信息见表1,板材规格为6000 mm ×1810 mm,企业现有剪床刀刃长度为2 010 mm。将上述信息输入本系统进行优化排样得到板材利用率为99.68%,使用两阶段算法和三阶段算法[9]得到板材利用率分别为82.95%和91.27%,3种算法的原材料利用率如表2所示,本文算法原材料利用率比两阶段算法提高了 16.73%,比三阶段算法提高了8.41%,使用本文算法可将板材分成4个最优子段,其中长度为1 824的子板重复使用了3次,如图5(a)所示,长度为526的子板使用1次,其最优排样方式如图5(b)所示,整张板材的最优排样方式如图6所示,从排样图可看出使用本文算法在切割工艺上与三阶段算法切割工艺基本相当。企业实际生产应用表明,在解决长板矩形优化排样问题方面本文算法明显优于两阶段算法和三阶段算法。

表1 矩形零件信息

表2 板材利用率
实例 2. 取欧洲切割与装箱特别兴趣组织官方网站http://www.fe.up.pt/esicup/上的RecPub_G4.zip 中50组零件(每组包括30类零件),作为待排零件,使用规格为2105 mm×1655 mm的板材,排样过程中不受剪床刀刃长度限制。使用本文算法和文献[4]T型算法、文献[5]三块式算法、文献[9]两阶段算法、文献[10]三阶段算法分别进行优化排样。各种算法的板材平均利用率如表3所示,在原材料利用率达到98%以上的情况下,本文算法在原材料利用率上比其他算法仍然有所提高。

图5 最优子段排样方式

图6 最优排样方式

表3 板材平均利用率
4 结 论
基于最优子段的矩形优化排样问题的求解主要集中在:同质条带求解、最优子段排样方式求解和长板分段方式求解。对算法中3个步骤的时间复杂性分析可知,算法中同质条带求解时间复杂度为O(1);最优子段排样方式求解的时间复杂度为O(m×LB×W);长板最优分段方式求解的时间复杂度为O(LB×L)。在时间复杂度方面本文算法与三块式排样算法基本相当,即系统计算速度与三块式算法基本相当,在计算时间方面本文算法能够满足企业实际需求。企业的实际应用证明,基于最优子段的矩形优化排样算法,在切割工艺相对简单的前提下,在优化能力方面明显优于两阶段算法和三阶段算法。文献实例验证表明,在没有剪床刀刃长度限制条件下本文算法在优化能力方面要优于 T型算法、三块式算法、两阶段、三阶段等算法。
[1] Gilmore P C, Gomory R E. Multistage cutting stock problem of two and more dimentions [J]. Operations Research, 1965, 13(1): 94-120.
[2] 黄文奇, 刘景发. 基于欧氏距离的矩形Packing问题的确定性启发式求解算法[J]. 计算机学报, 2006, 29(5): 734-739.
[3] 崔耀东, 黄健民, 张显全. 矩形毛料无约束二维剪切排样的递归算法[J]. 计算机辅助设计与图形学学报, 2006, 18(7): 948-951.
[4] 崔耀东. 生成矩形毛坯最优T形排样方式的递归算法[J].计算机辅助设计与图形学学报, 2006, 18(1): 125- 127.
[5] 潘卫平, 陈秋莲, 崔耀东, 等. 基于匀质条带的矩形件最优三块布局算法[J]. 图学学报, 2015, 36(1): 7-11.
[6] 崔耀东, 季君, 曾窕俊. 生成矩形毛坯最优两段排样方式的递归算法[J]. 南京航空航天大学学报, 2006, 38(1): 111-114.
[7] 崔耀东. 长板单一尺寸矩形毛坯定长分割优化排样[J].计算机工程, 2004, 30(7): 178-180.
[8] 姜永亮, 杨志强, 张诚一. 基于两阶段的分段单一矩形优化排样[J]. 计算机应用, 2011, 31(6): 1689-1691.
[9] Hifi M. Exact algorithms for large scale unconstrained two and three staged cutting problems [J]. Computational Optimization and Applications, 2001, 18(1): 63-88.
[10] Silva E, Alvelosa F, Valério de Carvalho J M. An integer programming model for two-and three-stage two-dimensional cutting stock problems [J]. European Journal of Operational Research, 2010, 205(3): 699-708.
Rectangular Optimal Layout Based on Best Sub Segments
Jiang Yongliang,Zhou Jun
(Campus Network Center, Hainan Normal University, Haikou Hainan 571158, China)
To effectively solve the long board rectangular optimal layout problems which is often encountered in the actual production of enterprises, rectangular optimal layout algorithms were studied and a rectangular optimal layout algorithm based on the best sub segments was proposed, which effectively solve long board rectangular optimal layout problems in actual production. Firstly based on dynamic programming algorithm all sub optimal layout modes were solved which is less than the shear blade length. Secondly with the best sub segments as layout parts, these segments were optimized on the long board and the rectangular optimal layout problems were converted to knapsack problems completely. Finally the integer programm ing algorithm based on branch and bound technique was used to solve the long board rectangular optimal layout problems. Enterprise’s practical application showed that the algorithm in solving the long board rectangular optimization problems is better than other algorithms.
rectangular optimal layout; best sub segment; dynamic programming algorithm; branch and bound technique
TP 391.7
10.11996/JG.j.2095-302X.2016020280
A
2095-302X(2016)02-0280-05
2015-07-29;定稿日期:2015-11-01
国家自然科学基金项目(71361008);海南省重点科技基金项目(ZDXM 20130080);海南省自然科学基金项目(612136)
姜永亮(1980–),男,河南漯河人,副教授,硕士。主要研究方向为计算机排样技术。E-mail:yongliangjiang@126.com
周俊(1974–),男,海南海口人,高级工程师,学士。主要研究方向为计算机排样技术。E-mail:zhjun@hainnu.edu.cn
